平面向量中的情境题赏析

王生云

(青海省海东市互助县第一中学)

«普通高中数学课程标准(2017 年版2020 年修订)»提出,选取恰当的问题情境是考查数学学科核心素养的重要载体.情境是高考数学命题的三大要素之一,情境是多样的、多层次的,包括社会热点、数学文化、现实生活、科学情境等.情境题是基于数学学科核心素养导向的命题,是为“问题”服务的,应以情境为命题背景,灵活进行设问,但需要注意情境背景与问题的融合.试题以考查知识、能力为基础,通过数学情境、社会情境或科学情境提出问题,进而综合考查学生的数学学科核心素养.笔者结合平面向量中的情境题来进行分析.

1 紧跟社会热点

例1 图1是2022年北京冬奥会会徽的图案,奥运五环的大小和间距如图2 所示.若圆的半径均为12,相邻圆圆心水平距离为26,两排圆圆心垂直距离为11.设五个圆的圆心分别为O1,O2,O3,O4,O5,则＝( ).

图1

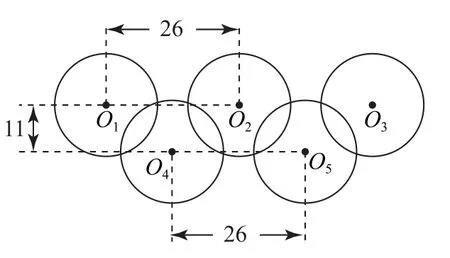
图2

图3

A.－507 B.－386

C.－338 D.－242

本题以社会热点事件中某一个图标为背景,结合平面向量的数量积来命制试题.背景材料的选取恰好符合平面向量的要求,是一道难得的好题.此类问题需要在理解情境的基础上,寻找合适的数学模型解决.这样的试题在高考和平常的模拟考试中出现的频率越来越高,同时对学生的要求也越来越高,学生不仅要掌握数学的基本知识和基本技能,还需要理解问题的本质,从情境中抽离出数学问题.

2 渗透数学文化

例2 “赵爽弦图”是数形结合思想的体现,是中国古代数学的图腾,还被用作第24届国际数学家大会的会徽.如 图4 所 示,大 正 方 形ABCD由4 个全等的直角三角形和中间的小正方形组成,若,E为BF的中点,则＝( ).

图4

以A为原点建立平面直角坐标系,如图5所示.不妨设AB＝1,BE＝x,则AE＝2x,所 以x2＋4x2＝1,解 得.设∠BAE＝θ,则,所以

图5

本题以学生熟知的“赵爽弦图”为背景立意试题,考查平面向量的基础知识及学生对基本问题的处理能力.

3 现实生活情境

例3 (多选题)图6是一款家居装饰物——博古架,博古架是类似于书架式的木器,其每层形状不规则,前后均敞开,无板壁封挡,便于从各个位置观赏架上放置的器物.某博古架的部分示意图如图7中实线所示,网格中每个小正方形的边长为1,则下列结论正确的是( _).

图6

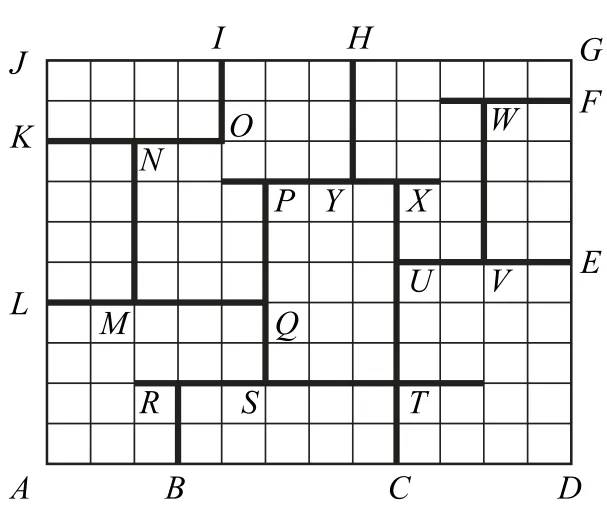
图7

以A为坐标原点,AD,AJ所在直线分别为x轴、y轴,建立如图8 所示的平面直角坐标系.

图8

综上,选AD.

情境题的背景是多样的,但来源于现实生活的少之又少,本题就是一道经典题.取现实生活为素材,进行试题命制,体现了命题者的智慧,给学生留下了宝贵的资源,让学生在理解熟悉情境的基础上,进一步提升解题能力.

学生能灵活应用数学知识解决各类问题的能力,是为将来在社会生活中用数学解决问题积累经验,对学生具有一定的挑战,也考查了学生的数学核心素养,所以好的题目来源于生活.

(完)