带电子空穴传导的H-SOFC电化学模型与电池性能

2023-11-10李会平

电池工业 2023年5期

李会平,李明

(1.华东理工大学无机材料系,上海 200237;2.武汉纺织大学化学与化工学院,湖北武汉 430073)

0 引言

质子导体固体氧化物燃料电池(H-SOFC)具有低工作温度和高燃料利用率等特点,正成为近年来能量转换装置的研究热点[1-3]。其工作原理是含氢燃料在催化剂的作用下释放出质子和电子。释放出的质子在电势的作用下穿过电解质,当到达阴极与电解质的三相界面(three phsae boundary,TPB)时,与从阴极通道扩散来的氧分子和从外电路来的电子反应生成水。生成的水汽在浓度差的作用下扩散至阴极通道,并被气流带走;释放的电子经阳极收集板汇集,从外电路流向阴极收集板,供阴极电极反应,并用于外部发电。

Han等人[4]研究了不同环境条件下掺杂了Sc、Y、In的BaZrO3质子导体电解质的电荷传输机理。研究发现,在还原气氛下,电解质内的电荷传输主要是通过质子传导实现的;而在氧化气氛下,电子空穴传导起到了显著作用。

对于以含氢物质为燃料,以空气或氧气为氧化剂的质子导体燃料电池来说,阳极处于还原气氛下,阴极处于氧化气氛下,电解质内的电荷传输既包括质子传导又包括电子空穴传导。电子空穴首先在阴极生成,然后在电势的作用下穿越电解质,形成内部导电(漏电);当电子空穴到达阳极时,被含氢燃料释放的电子捕获并终止。电子空穴形成的电池内部导电会降低电池的外部输出电压,从而恶化电池性能。Nakamura等人[5]针对一个简单的电池模型,采用电化学方法研究了电解质中质子和电子空穴电导率对电池效率和功率密度的影响,提出了对电池设计、工作条件和电解质材料选择的设想,以提升H-SOFC的开发工作,但其电池模型过于简单。

Zhu等人[6]应用缺陷化学理论,通过耦合Nernst-Planck-Poisson方程,构建了混合导电质子陶瓷燃料电池性能分析的理论模型。但模型过于复杂,仅在不考虑活化极化和浓差极化的前提下,求得了质子陶瓷电池的开路电压。

Zhang等人[7]基于带电粒子传输的Nernst-Planck方程,通过假定4步的电化学反应,导出了电子空穴传导的电流密度方程,形成了比较实用的质子和电子空穴混合传导质子固体氧化物电池电化学性能分析的理论模型;Putilov等人[8,9]注意到了实际使用的电池沿电解质横截面和沿电池沟道流动方向气体组分的不均匀变化,从电化学角度研究了电池横截面和沟道流动方向的电池参数的变化规律,并提出了电子空穴有效电导率的概念;Zhang等人[10,11]发展了Putilov等的电子空穴有效电导率的概念,通过构建等效电路,从理论和实验角度确定了电子空穴电导率等材料性质参数,使电池的性能模拟工作具有更普遍和更实用的意义。

Zhang等人[7]的工作建立了电解质中电荷微观传输理论与电池宏观性能计算,具有理论开创意义,但常数的电子空穴电导率的使用理论不够全面。文献[8]和[9]提出了电子空穴有效电导率等概念。然而,这些文献中假设两侧恒定输出电压和电池温度一致,这与电池的实际工作状况存在差异。另外,文献[10]和[11]采用了电子空穴有效电导率等参数,并提出了通过等效电路确定有效参数的做法,这是值得肯定的,但这些文献提出的电池活化极化过电势的公式过于复杂。

基于文献[7]的理论框架,采用电荷有效参数的概念,参照文献[12]提出的分析纯质子传导的质子导体固体氧化物燃料电池的电化学模型的做法,构建了带电子空穴传导的H-SOFC的电化学性能分析模型,并将电池模拟研究分成电池电化学性能分析和电池堆性能模拟两个方面。在电池电化学性能分析中,通常只考虑电池本身的性能,不考虑沿电池沟道流动方向的温度变化。而在电池堆性能模拟中,需要同时考虑沿电池沟道流动方向的气体组分和温度的变化,这样可以更全面地了解电池的性能。

1 电荷有效电导率定义与使用

Zhang等人[7]研究了阳极为Ni-BZY、电解质为BZY、阴极为LSCF电池的电化学行为。在总结文献的基础上,概括了该类电池的4步电化学反应机理。

4步电化学反应过程如下。

以假定质子和电子空穴的电导率是常数为前提,通过求解Nernst-Planck方程,Zhang等人[7]导出了电子空穴传导电流密度方程:

(1)

式中,PH2,a、PH2,c分别为阳极和阴极的氢气分压,Pa;Jext为外电路的电流密度,A/m2;dele为电解质的厚度,μm;σh*、σH+分别为电解质的电子空穴和质子电导率,S/m,可进一步表示为[11]

(2)

(3)

式中,σ0h、Eh、σ0H、EH分别为电子空穴和质子电导率的指前因子和活化能;PO2、PH2O、P0分别为氧气、水蒸气和环境压力;T为温度;R为气体常数。

从式(2)和式(3)可见电解质的电子空穴电导率σh*和质子电导率σH+是气体组成和电解质温度的函数。对实际工作的电池来说,电解质横截面上和沿沟道流动方向气体的组分是不均匀的。常数电子空穴和质子电导率不够严谨。按某种方式取电解质横截面或沿沟道气流方向平均值的做法是合理的。Zhang等人[10,11]采纳了Putilov[8,9]的设想,取电解质横截面上电导率的平均值进行计算,并定义为有效电导率,使之从实验求得的σ0h、Eh、σ0H、EH成为材料的特性参数。电荷(质子和电子空穴)的有效电导率σk,eff定义如下:

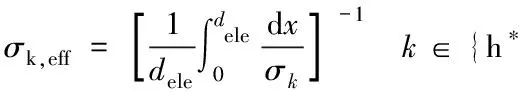
(4)

式(4)中,x为电解质厚度方向。式(4)表示有效电导率是电解质厚度方向的电导率的平均值。

式(4)定义的有效电导率可通过数值积分方法求得。当电导率不是空间位置的函数时,问题退化为常数电导率问题。

在算得电子空穴和质子的有效电导率后,由式(1)可算出电子空穴的电流密度Jh*。

由图1的电荷传导模型可知,质子传导的电流密度JH+与电子空穴的电流密度Jh*有如下关系:

JH+=-(Jh*+Jext)

(5)

Jext可由外电路测得。在确定外部电流密度Jext后,根据事先确定的电解质材料参数σ0h、Eh、σ0H、EH、电池温度和电池两侧的气体组分,由式(2)、式(3)、式(4)可算出电子空穴和质子的有效电导率,由式(1)和式(5)可分别求出电子空穴和质子的电流密度,进而可进行电池的电化学性能分析。

2 电化学模型与电池效率

2.1 电化学模型

由H2与O2反应的总反应方程,可得H-SOFC的可逆电势E为

(6)

式中,E0为标准电动势,是温度的函数[7];PH2O,c、PO2,c分别为阴极通道中H2O、O2的分压;PH2,a为阳极通道中的H2分压。

电池输出电压V是电池可逆电势减去各类极化损失后的值[7,11,12]。

V=E-(ηconc,a+ηconc,c+ηact,a+ηact,c+ηohm)

(7)

式中,ηohm为欧姆极化损失;ηconc,a、ηconc,c、ηact,a、ηact,c分别为阳极、阴极浓差极化损失和活化极化损失。

2.1.1 欧姆极化损失

欧姆极化损失包括质子和电子在电极层的传导阻力和电解质内的传导阻力。一般来说,电极层的传导阻力很小,可忽略。传导阻力可用欧姆定律描述。电解质的欧姆电压降(ηohm)与电流密度(JH+)和电导率(σH+,eff)之间有如下关系。

ηohm=JH+dele/σH+,eff

(8)

质子的有效电导率可由式(2)—式(4)计算。

2.1.2 浓差极化损失

电化学反应发生在阴极、阳极与电解质三相界面上。由于扩散传质阻力,通道内气体组分的浓度有别于三相界面的浓度,会产生电势损失。

浓差极化损失与气体在通道中的平均浓度和三相界面的浓度有如下关系:

(9)

(10)

式中,CH2,a、CH2,TPB分别为H2在阳极通道和三相界面的浓度;CO2,c、CO2,TPB分别为O2在阴极通道和三相界面的浓度;CH2O,c、CH2O,TPB分别为H2O在阴极通道和三相界面的浓度。

三相界面的气体组分浓度可通过分析气体组分在通道和电极层中的传质过程得到。气体组分在多孔材料的传质过程是一个复杂的问题,不同的研究者有不同的处理方法,文献[7]用尘气模型(dusty gas model,DGM)关联三相界面气体组成与沟道内气体组分之间的关系。文中假设气体组分在通道的流动为柱塞流动,在电极材料层中的传质为一维扩散传质,应用Fick扩散定律,导出了如下关系[12-13]:

(11)

(12)

(13)

式中,δa、δc分别为阳极和阴极厚度;DH2,eff为H2在阳极通道的有效扩散系数;DO2,eff、DH2O,eff分别为O2、H2O在阴极通道内的有效扩散系数[12]。

2.1.3 活化极化损失

发生在电极表面的电化学反应需要克服一定的势垒才能进行,会导致一定的电势损失。活化极化损失通常用Butler-Volmer电流密度方程描述,其一般形式为

(14)

式中,n为转移的电子数;α为电荷转移系数,通常取0.5;j0为交换电流密度,阴、阳极的交换电流密度如下[7]。

j0,a=γaexp(-Eact,a/RT)

(15)

j0,c=γcexp(-Eact,c/RT)

(16)

整理式(14),对阳极,有

应用双曲正弦函数的定义,sinh(x)=(ex-e-x)/2,

取反函数,整理有

(17)

(18)

综合阴阳极,有

(19)

electrode∈{a,c}

2.2 电池效率

2.2.1 Faraday效率

Faraday效率原指离子电流占总电流的比例。在带电子空穴传导的H-SOFC电池中,主要有电池外部电流密度Jext和电子空穴传导形成的内部电流密度(即漏电电流密度Jh*)。为了讨论方便,将Faraday效率定义为电池的外部电流密度Jext与总电流密度(Jext+Jh*)的比值[7,11],其间接反映了电子空穴传导的导电效率。

(20)

当没有电子空穴传导时,流过电池内部的电流密度与外部的电流密度相等,Faraday效率等于1。当有电子空穴传导(漏电)时,外部电流密度小于总电流密度,Faraday效率小于1。Faraday效率越接近0,电子空穴传导作用越大,电池漏电越厉害。

2.2.2 能源利用效率

燃料电池的作用是通过电化学反应消耗燃料通道中的燃料(如H2)对外发电。燃料电池的能源利用效率ηegy可用式(21)表达[7,8]。

(21)

式中,ΔHH2,DW为H2燃烧低位热值,kJ/mol;NH2为燃料通道消耗的H2,可用下式描述。

(4)创新驱动效应偏低，自主研发能力有待加强。湖北省汽车零部件产业集聚了很多仅有组装生产功能而无研发能力的零部件企业，但技术研发能力强、营业规模超10亿元级的龙头企业还很少。另外，还缺乏汽车零部件方面的公共创新服务平台，导致整体创新驱动效应明显不足，汽车零部件技术研发、检验检测、产业孵化等公共配套服务缺乏，无法有效促进整体汽车零部件技术和生产工艺的提升。

(22)

上述方程构成了带电子空穴传导的H-SOFC电池性能分析模型。输入相关参数,计算可得电池输出电压、电势损失,进而分析电池效率。

3 结果与讨论

应用上述模型对带电子空穴传导的H-SOFC电池进行了计算研究。计算中用到的物性参数取自文献[7],电池气体组成和电极特性参数取自文献[12],如表1所示。

3.1 电池基本性能

当温度为650 ℃、电解质厚度为20 μm时,电池的输出电压和电势损失如图1所示。

表1 计算中用到的物性参数和电池参数[7,12]Table 1 The material physical properties and cell parameters used in our calculations[7,12]

续表

图1 电池输出电压和各种电势损失随输出电流密度的变化Fig.1 The change of output voltage and various potential losses with output current density

从图1中可见,带电子空穴传导的H-SOFC输出电压和各种电势损失随外部(输出)电流密度的变化规律与纯质子传导的H-SOFC的变化规律一致[12]。随着输出电流密度的增大,电池的输出电压降低,各种极化损失增加。与此同时,浓差极化损失较小,电池的主要电势损失来自电解质的欧姆极化损失和电极的活化极化损失。然而,与纯质子传导的H-SOFC相比,带电子空穴传导的H-SOFC具有更低的开路电压(图1中开路电压约为0.9 V,低于文献[12]中的1.0 V)。这主要是由于电子空穴传导引起了漏电现象。

电子空穴传导的H-SOFC的漏电电流密度与电池输出电池密度和电池温度的关系如图2所示。

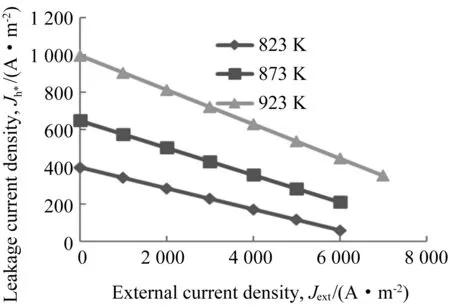
图2 漏电电流密度随输出电流密度的变化Fig.2 The change of leakage current density with output current density

由图2可知,随着输出电流密度的增大,带电子空穴传导的H-SOFC的漏电电流密度逐渐减小,这与公式(1)是相符的。

当输出电流(外部电流)为零时,漏电电流密度达到最大值。外部电流为零意味着电池处于开路状态,这说明带电子空穴传导的H-SOFC的漏电主要发生在接近开路的时候。由图2还可知,电池温度越高,漏电越严重。因此,带电子空穴传导的H-SOFC不宜在高温中工作。

电池Faraday效率和能源利用效率如图3所示。从图中可知,Faraday效率随着输出电流密度的增大而逐步增大。在低电流密度下,效率的增大比较明显。在输出电流密度约为2 000 A/m2时,Faraday效率达70%。随后,Faraday效率的增长逐渐减缓,并最终趋于100%。这表明,在输出电流密度较小时,漏电现象最为明显,接近于开路状态。

图3 电池效率与输出电流密度的关系Fig.3 The curve of cell efficiency with output current density

由图3还可知,随着输出电流密度的增大,电池的能源利用效率会先迅速增大,达到最大值后又逐渐降低。这说明从能源利用效率的角度来看,电池应该在较小的输出电流密度范围内工作。在文中研究的条件下,当输出电流密度约为1 800 A/m2时,能源利用效率达到最大值,约35%,此时对应的输出电压约为0.65 V。

3.2 电池温度的影响

前已述及,质子导体固体氧化物燃料电池的主要电势损失包括电解质的欧姆损失和电极的活化极化损失。欧姆极化损失主要受到材料的电导率和电解质厚度的影响,而电导率与电池温度直接相关。为此,研究了电池温度对欧姆极化损失的影响。

图4 电池温度对电势损失和电池效率的影响Fig.4 The influence of operating temperature on various potential losses and cell efficiency

由图4(a)和图4(b)可知,随着输出电流密度的增大,欧姆极化和活化极化损失逐渐增大。同时,电池温度对这两种损失也有影响,即温度越高,欧姆极化和活化极化损失越小。输出电流密度较小(约800 A/m2)时,欧姆极化损失出现反常现象:当输出电流密度小于800 A/m2时,温度越高,欧姆极化损失越大。这主要是因为输出电流密度较小时(接近电池开路),漏电电流随温度升高而迅速增大(图2)。因此,对于工作在小输出电流密度的电池来说,其温度不宜过高。

由图4(c)可知,温度越高,Faraday效率越低。随着温度的升高,电池外部电流密度在总电流密度中占的比重下降,即高温下的漏电作用更加明显。

由图4(d)可知,在一定温度下,能源利用效率随着输出电流密度的增大呈现先迅速升高,达到最大值后再逐渐降低的趋势,最大能源利用效率的值增大,且对应的输出电流密度向较小的值偏移。例如,在923 K时,最大效率为35%,对应的输出电流密度为2 000 A/m2;在873 K、823 K时,对应的最大效率分别为38%、40%,输出电流密度分别为1 000 A/m2、800 A/m2。

3.3 电解质厚度的影响

电解质厚度对Faraday效率和能源利用效率的影响如图5所示。

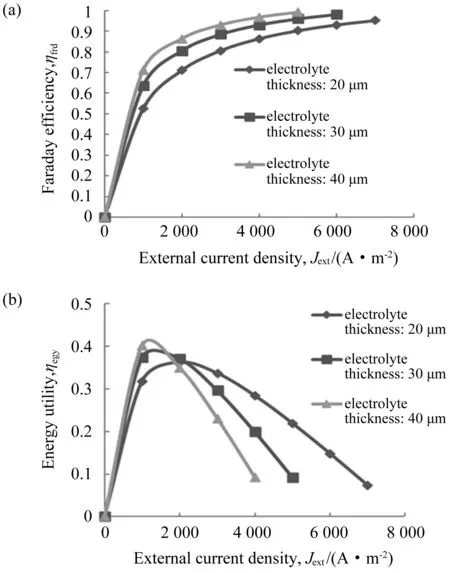
图5 电解质厚度对电池效率的影响Fig.5 The influence of electrolyte thickness on cell efficiency

由图5(a)可知,电解质越薄,电池Faraday效率越低,即外部电流密度所占比重越小,漏电作用越明显。

由图5(b)可知,电解质越厚,其对应的最大能源利用效率越高。同时,达到最大效率时对应的输出电流密度会变小。根据文中研究的条件,电解质厚度为20 μm、30 μm和40 μm时,所对应的最大能源利用效率分别为35%、38%、42%,输出电流密度分别为2 000 A/m2、1 400 A/m2、1 200 A/m2。

综上所述,带电子空穴传导的H-SOFC的漏电行为主要发生在小的输出电流密度,即接近开路电压的时候,电池温度越高,电解质越薄,越容易发生漏电。

从能源利用效率角度考虑漏电行为,电池应工作在较小的输出电流密度和适中的工作温度区域,同时电解质的厚度不宜太薄。根据文中的研究条件,当电池在600 ℃的工作温度下,外部电流密度为1 400 A/m2,电解质厚度为30 μm时,电池的能源利用效率约为40%。