一类特殊凸体的照亮与覆盖

何 婵, 赵艳萍, 吴森林

(中北大学 数学学院,山西 太原 030051)

0 引 言

集合K⊂n的相对内部、相对边界、内部和边界分别记作relintK,relbdK,intK和bdK.对于任意大于1的整数m,用[m]表示集合{1,2,…,m}.设K⊂n,若存在K1,K2,…,Km满足K⊂∪i∈[m]Ki,则称K1,K2,…,Km是K的一个覆盖.设x,y∈n,把经过x和y的直线记作〈x,y〉,即

把连接x和y的线段记作[x,y],即

若对K中任意2点x和y,有[x,y]⊂K,则称K为一个凸集.若凸集K是一个含内点的紧集,则称K是一个凸体.用Kn表示n中所有凸体构成的集合,用o表示n的原点.

设K∈Kn.用c(K)表示覆盖K所需的K的内部的平移的最小数目,简称覆盖数.关于c(K)的上界,源于文献[1]的关于凸体覆盖的Hadwiger猜想(简称为H-猜想):

H-猜想对任一K∈Kn,有

c(K)≤2n,

且c(K)=2n当且仅当K是一个仿立方体.该猜想分成2部分:一是不等式部分,即“c(K)≤2n,∀K∈Kn”;二是等式部分,即“c(K)=2n当且仅当K是一个仿立方体”.H-猜想在n=2时被完全解决:Levi[2]证明了对任意的二维凸体K,c(K)≤4并且c(K)=4当且仅当K一个是平行四边形.但在n=3时H-猜想就已是很困难的公开问题.目前,在三维空间中H-猜想已经有了一些重要的进展.例如,Lassak[3]证明了c(K)≤6对三维空间中的等宽体均成立;此外,Lassak[4]还证明了c(K)≤8对三维空间中任意中心对称的凸体均成立;Papadoperakis[5]证明了c(K)≤16对任意的三维凸体均成立.关于H-猜想及相关问题的其他重要工作可参见[6-14].

设K⊂n,包含K的最小仿射集的维数称为K的仿射维数,记作dimK.设K⊂n是一个紧凸子集,x∈relbdK,u是n中异于原点o的一个向量(称为一个方向).若存在λ>0使得x+λu∈relintK,则称x被方向u照亮.令D是由若干方向构成的集合,若relbdK中的每个点均可被D中的某个方向照亮,则称D可以照亮relbdK.关于凸体覆盖和照亮的一个经典的结果指出,c(K)等于照亮relbdK所需的方向的最小的数目.若方向集D能够照亮relbdK并且D的基数等于c(K),则称D是K的一个照亮系统.注意到,当K是一个凸体时,K的相对内部与内部等价.

本文中,笔者主要考虑一类特殊的三维凸体的照亮问题,并给出该类凸体的覆盖数的上界.

1 准备工作

引理1[15]若K∈n是一个紧凸集,p∈relintK,D={vi|i∈[m]}是K的一个照亮系统,则存在2个实数λ>0和α∈(0,1),使得对于每个x∈K,均存在i∈[m]满足

x+λvi∈α(relintK)+(1-α)p.

引理2[16]若K∈Kn,且D是由若干方向构成的集合,则D可以照亮K的边界当且仅当D可以照亮K的每个端点.

引理 3设K∈Kn,a,b∈bdK.若线段[a,b]⊂bdK且z∈[a,b]{a,b},则对于K的每个过z点的支撑超平面H均有[a,b]⊂H.

证设H是K的一个过z点的支撑超平面,则存在非零向量c∈n和实数α使得

H={x∈n|x·c=α},

其中x·c是向量x与c的数量积.显然,z·c=α.不失一般性,假设对于任意的x∈K,有x·c≤α.由于z∈[a,b]{a,b},故存在μ∈(0,1)使得z=μa+(1-μ)b,从而

z·c=(μa+(1-μ)b)·c=μa·c+(1-μ)b·c≤α.

因此a,b∈H,这意味着[a,b]⊂H.

定义1[17]设K是一个紧凸集,a,b∈K且a≠b.若存在K的一对平行的支撑超平面H+和H-使得a∈H+且b∈H-,则称[a,b]是K的一条仿射直径,称a和b是一对对径点.

引理4[17]设K∈Kn,a,b∈K,则[a,b]是K的一条仿射直径当且仅当[a,b]是含于K且平行于直线〈a,b〉的最长的线段.

引理5[18]设K∈Kn,x,y∈bdK.若x和y不是对径点,则存在一个同时照亮这2点的方向.

设K∈Kn且o∈intK.由于K的闵科夫斯基泛函‖·‖K在n中是连续的,从而有下列结论:

命题1设C是K⊂n的一个紧凸子集,u是n中的一个方向.如果对于每个x∈C,都存在λx>0使得x+λxu∈intK,那么存在一个正数λ满足x+λu∈intK,∀x∈C.

证对于每个x∈C,令

Λ(x)=sup {η≥0|x+ηu∈intK},

Λ=inf {Λ(x)|x∈C}.

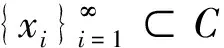
矛盾,从而Λ>0.令λ=Λ/2,则x+λu∈intK,∀x∈C.

2 主要结果

定理1设K∈K3,若存在一个过原点o的超平面H以及H中的3个方向d1,d2,d3,使得对任意平行于H且与intK相交的超平面H′,H′∩K的任一相对边界点均可被d1,d2,d3其中之一照亮,则照亮bdK至多需要9个方向.

H′∩intK≠∅,dim(H′∩K)=2,x∈relbd(H′∩K).

根据文献[12],有relint(H′∩K)=intK∩H′.因此,存在i∈[3]使得x能够被di照亮.

接下来,将根据T和B的仿射维数分成以下6种情形来讨论bdK的照亮问题.

情形1 dimT=dimB=0.

不妨设T={a},B={b}.令

d4=-a,d5=-b,

则bdK能被方向集{di|i∈[5]}照亮.

情形2 {dimT,dimB}={0,1}.

不妨设T=[a,c],B={b}.令

d4=-a,d5=-b,d6=-c,

由引理2可知bdK能被方向集{di|i∈[6]}照亮.

情形3 dimT=dimB=1.

不妨设T=[a,c],B=[b,d],令

d4=-a,d5=-b,d6=-c,d7=-d,

则bdK能被方向集{di|i∈[7]}照亮.

情形4 {dimT,dimB}={0,2}.

不妨设T={a},dimB=2.用o(B)表示含于B的面积最大的椭球的中心点.令

由于每个平面凸体的照亮系统中最多包含4个方向[8],设D={vi|i∈[4]}是由4个方向构成的集合并且满足对每个x∈relbdB,存在vi∈D,λ>0和α∈(0,1)使得

x+λvi∈αB+(1-α)o(B)⊂relintB.

由引理1可知这样的λ和α是存在的.令y是αB+(1-α)o(B)中的任意一点,则存在γy>0使得y+γyu∈intK.否则,〈y-u,y+u〉是K的一条过y点的支撑直线,这与K只存在唯一一个过y点的支撑超平面矛盾.因此由命题1可知,存在一个公共的实数γ>0使得对每个y∈αB+(1-α)o(B),均有y+γu∈intK.令

则对任意的x∈relbdB,有

x+λv′i=x+λvi+γu∈intK,

这意味着x作为K的边界点可被v′i照亮.令d4=-a,则方向集{di|i∈[4]}∪{v′i|i∈[4]}可以照亮K的边界.

情形5 {dimT,dimB}={1,2}.

不妨设dimT=1,dimB=2.若B不是平行四边形,则B作为一个平面凸体只需要3个方向就可被照亮[8].基于情形3的证明,照亮bdK最多需要8个方向.

接下来,考虑B是平行四边形的情况.令

B=conv{a,b,c,d},T=[e,f].

如果a,b,c,d,e,f中存在2个点是非对径点,那么由引理2和引理5可知,bdK可被8个方向照亮.如果这些点都是两两对径的,由平行四边形的性质可知[a,d]与[(a+b)/2,(c+d)/2]等长且二者所在直线平行,故由引理4可知(a+b)/2和(c+d)/2是对径点,从而存在K的一组过这两个点的平行的支撑超平面H3和H4,根据引理3有

[a,b]⊂H3,[c,d]⊂H4.

同理,(a+d)/2和(b+c)/2也是对径点,从而存在K的一组分别过点(a+d)/2和(b+c)/2的平行的支撑超平面H5和H6满足

[a,d]⊂H5,[b,c]⊂H6.

令P表示由H1,H2,H3,H4,H5,H6决定的平行六面体,则K⊂P,B是P的一个真面,且a,b,c,d是P的4个顶点.令a′,b′,c′,d′表示P的其余顶点,如图1,则T⊂T′=conv{a′,b′,c′,d′}.令

图1 平行六面体P Fig.1 The Parallelepiped P

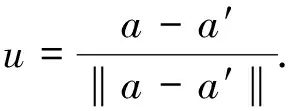
对于任意的x∈P,令xu表示x点沿着u方向在B上的投影.由于e和f是对径点,故e,f∈relbdT′.那么,eu∈relbdB,[e,eu]⊂bdK.令

则存在γ>0,dj∈{d1,d2,d3}和λ1>0使得e′=e+γu,e′+λ1dj∈intK.不妨设dj=d1.

令

接下来,构造可以照亮bdK的方向.令

w1=d1+utanθ,w2=d2,w3=d3,w4=-f,

w5=-a,w6=-b,w7=-c,w8=-d.

则点f,a,b,c,d可以分别被w4,w5,w6,w7,w8照亮.对于点e,根据w1的构造,有

e+λ1w1=e+λ1d1+γu∈intK,

这就意味着e能够被w1照亮.对于bdK{T,B}中的任意一点x,存在λx>0和i∈{1,2,3}满足x+λxdi=z∈intK.如果di等于d2或者d3,那么w2或者w3可以照亮x.如果di=d1,将证明w1可以照亮x.

注意到[x,xu]⊂bdK或者[x,xu]{x,xu}⊂intK,并且对任意的μ∈(0,1],

μz+(1-μ)zu∈intK.

令A表示以x,z,zu,xu为顶点的4边形,显然A是平行四边形.根据文献[19]中的定理 2.36,有

relintA⊂intK.

由w1的构造可知,从x出发沿w1方向的射线必与relintA相交,故存在λ>0使得

x+λw1∈intK.

因此,bdK能被方向集{wi|i∈[8]}照亮.

情形6 dimT=dimB=2.

根据T和B的形状下面分为3种情况进行讨论.

1)T和B中只有一个是平行四边形.不妨设B是平行四边形,a,b,c,d是B的4个顶点.如果这些顶点中存在非对径点,不失一般性,假设a和b不是对径点,那么c和d也不是对径点,从而由引理5可知照亮bdK至多需要8个方向.如果这4个顶点是两两对径的,那么根据情形5,K含于一个以B为基底的平行六面体P′中,如图2.令a′,b′,c′,d′表示P′的除a,b,c,d外的4个顶点,T′=conv{a′,b′,c′,d′}=H1∩P′,u=(a-a′)/‖a-a′‖,则T⊂T′,并且对于任意的x∈relbdT,存在γx>0,λx>0和i∈{1,2,3}使得

图2 平行六面体P′Fig.2 The Parallelepiped P′

x+γxu=x′∈KB,x′+λxdi∈intK.

令

wi=di+utanθ,i∈[3],

w4=-a,w5=-b,w6=-c,w7=-d.

类似地,可以证明{w1,w2,…,w7}能够照亮bdK.

2)T和B均为平行四边形.设a,b,c,d是B的4个顶点,e,f,g,h是T的4个顶点.故在a,b,c,d,e,f,g,h中必存在一组非对径点.否则,K是一个平行六面体,与定理条件矛盾.

不失一般性,假设e和f不是对径点,那么g和h也不是对径点.如果B的顶点中也存在一组非对径点,则照亮bdK至多需要7个方向.假设B的顶点两两对径,则K含于以B为基底的平行六面体中,接下来的证明与(1)类似.因此,在这种情形下至多需要7个方向就可把bdK照亮.

3)T和B均不是平行四边形.由于照亮一个非平行四边形的平面凸体只需3个方向,故T和B可分别被3个方向照亮.因此,bdK可被9个方向照亮.证毕.

注事实上,对满足定理1的条件的凸体K,有c(K)≤9.由定理1的证明可看到,除T和B均不是平行四边形的情况外,其余情况下照亮凸体K均至多需要8个方向,从而证明了在这些情况下Hadwiger猜想不等式部分的正确性.