基于数据融合技术的电力系统鲁棒动态状态估计方法
2023-11-10马玉玲李朝祥曹中枢杨昌华
马玉玲,李朝祥,曹中枢,潘 龙,杨昌华,杨 哲
(1.国网宁夏电力有限公司培训中心,宁夏银川 750000;2.三峡大学电气与新能源学院,湖北宜昌 443000)
0 引言
相量量测单元(Phasor Measurement Unit,PMU)在电力系统中的广泛布置,但又无法完全替代传统的监控与数据采集系统(Supervisory Control And Data Acquisition,SCADA),故而在很长一段时间内,PMU 和SCADA 的采集数据将共存于电力系统[1-4]。在状态估计领域,如何充分有效地将SCADA 数据和PMU 数据结合使用,最大化估计性能,是当前研究的一个重点[5-10]。总体而言,将SCADA 数据和PMU数据结合使用的主流方法有2 种:一种是将SCADA与PMU 数据直接混合,不对数据源、特点和精度等进行区分,直接用于电力系统状态估计[11-15];另一种是将SCADA 与PMU 数据在2 个阶段分开使用,进行两阶段的状态估计[16-17]。
文献[5-7]基于混合数据处理方法,直接将PMU与SCADA 数据混合使用,该方法直接简单,易于实施,然而却需要将程序中的雅可比矩阵等关键部位进行修改,使得其程序扩展性不强[18-22]。同时,在每一断面进行滤波时,采用PMU 和SCADA 数据混合共同构造量测方程进行滤波处理,将造成PMU 和SCADA 数据相互影响,使得量测精度较低的SCADA数据对量测精度较高的PMU 数据造成污染[19-25]。
文献[8-10]基于两阶段处理方法,在第一阶段利用预测值与SCADA 数据相结合进行滤波处理,得到一阶段估计值,然后将一阶段估计值与PMU数据结合作为第二阶段量测进行滤波估计,并得到最终结果。该方法虽然有效避免了混合数据处理过程中PMU 和SCADA 数据的相互影响,但由于在每一断面的处理中都需要进行两阶段的滤波,在连续多断面处理中,损失了计算效率。数据融合理论[22-27]主要用于处理非同源的数据信息或状态,并将其以最佳方式进行融合,以获得最优结果。从研究意义上,相对于从单方面获取的单一的独立源信息,由数据融合理论得到的最终融合信息,其质量将得到明显提高。
为此,本文针对在连续多断面动态状态估计(Dynamic State Estimation,DSE)中,现有混合数据处理方法存在的两者数据相互影响以及两阶段处理方法存在的效率低下问题,提出了一种基于数据融合技术的电力系统鲁棒DSE 方法。本文创新点主要有2 个:1)在文献[27]基础上,对第三步进行了改进,提出了基于改进变点重复检测的方法以确定PMU 的最优缓冲长度,从而将PMU 和SCADA 数据归一到同一断面下。本文相对文献[27]的改进之处为不再是两两之间进行变点检测,而是系统性的扩大子集变点检测,有利于系统性的变点检测;2)本文采用数据融合技术,在每一断面内,分别用预测值与SCADA 数据、预测值与PMU 数据基于指数权估计进行独立并行滤波计算,然后将滤波后的两组估计值基于数据融合技术进行状态融合,得到最佳估计值。本文所提方法不仅能够有效避免精度较低的SCADA 数据对精度较高的PMU 数据的影响,且两组滤波可独立进行,极大提高了算法的效率。
1 无迹卡尔曼动态状态估计方法
1.1 动态状态和量测模型
电力系统中,动态状态和量测模型可表示为[13-14]:
式中:k为k时刻;Xk为状态向量;Zk为量测向量;f为预测函数;h为量测方程;ωk为系统状态噪声;νk为量测噪声。
1.2 两参数平滑预测法
使用两参数(α,β)平滑预测法进行状态预测,预测函数f()为:
式中:,为k时刻状态预测值向量和估计值向量;ak,bk为k时刻水平预测分量向量和倾斜预测分量向量;α,β为平滑参数,位于0~1 之间。
1.3 无迹变换
1.3.1 构造Sigma点集
在初始状态,若已知n维状态估计值与n×n维方差阵Px,0,Sigma 点集{} 可按式(3)构造[15-17]:
式中:Px,k为k时刻n×n维方差阵;为构造的Sigma 点。
1.3.2 非线性预测变换
使用预测函数f(·)对Sigma 点集{} 做非线性预测变换[18-19]:
1.3.3 统计预测均值与方差
式中:ωi=1/2nk+1为预测状态量。
+1的方差为:
式中:,k+1为k+1 时刻预测状态方差阵。
定义+1与真值xk+1误差为e1,k+1,有:
式中:xk+1为k+1 时刻状态真值;e1,k+1为k+1 时刻状态预测误差。
2 基于改进变点重复检测的断面归一化处理
由于PMU 和SCADA 数据的采样频率不同,为将两者数据有效结合,首先须将时间尺度统一到同一断面下,进行断面归一化处理[20-21]。本文在文献[27]基础上,对第三步进行了改进,提出了基于改进变点重复检测的方法以确定PMU 的最优缓冲长度,从而将PMU 和SCADA 数据归一到同一断面下,具体步骤如下:
1)假设SCADA 采样数据时间间隔为Nt秒,PMU 每秒采样数为n个,在SCADA 采样间隙内,PMU 缓冲区采样数目为N=Nt×nr个,将其分成nsubset个子集(nsubset=Nt),每个子集采样数目为nmeas=n,可表示为:Z(1),Z(2),…,Z(nsubset)。
2)首先对Z(nsubset) 进行变点检测。计算Z(nsubset)内nmeas采样量测的标准差,并与阈值比较,若小于阈值,则无变点,Z(nsubset)均位于最优缓冲区,转步骤(3);否则,取Z(nsubset)内最新的一个PMU采样量测,作为该PMU 测点的量测值,计算中止。
3)基于Matlab 内嵌函数ttest2 对Z(nsubset) 与Z(nsubset-1),[Z(nsubset),Z(nsubset-1)]与Z(nsubset-2),…,[Z(nsubset),Z(nsubset-2),…,Z(2)]与Z(1)分别进行变点检测。本文相对文献[27]的改进之处为不再是两两之间进行变点检测,而是系统性的扩大子集变点检测,有利于系统性的变点检测。
最优缓冲长度计算式为:
式中:Nop_bf为最优PMU 缓冲长度;hi(i=1,2,…,nsubset-1)为变点检验结果;上横线为逻辑非运算。
对各PMU 测点,分别按这3 个步骤确定最优缓冲长度,并统计最优缓冲区内PMU 的均值与方差,作为与SCADA 数据等效断面的PMU 数据,实现断面归一化处理。
3 基于数据融合的鲁棒DSE方法
本文所提基于数据融合的电力系统鲁棒DSE方法,将归一化后的PMU 和SCADA 数据分别作为独立的数据源,在每一断面内,分别用预测值与SCADA 数据、预测值与PMU 数据基于指数权估计进行独立并行滤波计算,然后将滤波后的两组估计值基于数据融合技术进行状态融合,得到最佳估计值。两组滤波可独立进行,极大提高了算法的效率。
3.1 基于指数权估计的SCADA滤波
利用k+1 时刻的预测值k+1和SCADA 量测z1,k+1构成第一组量测,量测方程为:
k+1时刻,第一组量测误差方差阵Σ1,k+1为:
式中:R1,k+1为v1,k+1的方差阵。
基于指数权估计方法,目标函数构造如下:
式中:z为量测量;h(x)为量测方程;W为指数权函数;c(x)为等式约束。
利用Lagrange 乘子法和Newton 法求解,得第j次迭代状态修正方程为:
收敛判据为:
收敛后,k+1 时刻第一组量测的状态估计值为(1,k+1),状态误差方差阵Γ1,k+1为:
3.2 基于指数权估计的PMU滤波
利用k+1 时刻的预测值k+1和PMU 量测z2,k+1构成第二组量测,量测方程为:
可简写为:
k+1时刻,第二组量测误差方差阵Σ2,k+1为:
式中:R2,k+1为k+1时刻v2,k+1的方差阵。
同理,基于指数权估计建立目标函数并求解,得状态更新方程为:
收敛判据为:
收敛后,k+1 时刻第二组量测的状态估计值为(2,k+1),状态误差方差阵Γ2,k+1为:
3.3 基于数据融合技术的状态融合
数据融合技术是一个较为新颖的研究方向和领域,该理论主要用于处理不同类的数据信息或状态,并将其进行数据信息融合,以获得最优融合结果。相对于从单方面获取的单一独立源信息,由数据融合理论得到的最终融合信息,其质量将得到明显提高。本文在状态估计领域,借鉴数据融合技术[11-12],旨在结合SCADA 和PMU 数据,将SCADA 和PMU 测量视为2 个独立的信息源并加以处理,并将所得结果进行融合,以获得最优融合结果。
由基于SCADA 数据的状态估计值(1,k+1)和方差Γ1,k+1、基于PMU 数据的状态估计值(2,k+1)和方差Γ2,k+1,通过下式进行融合,得到k+1时刻的最终估计值:
基于数据融合技术的并行滤波计算,不仅充分利用了PMU 和SCADA 数据,有效避免了混合数据滤波中精度较低的SCADA 数据对精度较高的PMU数据的影响,且有效提高了算法的计算效率。
3.4 鲁棒DSE方法计算步骤
基于数据融合的鲁棒DSE 方法详细计算流程如图1 所示。

图1 基于数据融合的改进鲁棒动态估计流程图Fig.1 Flow chart of improved robust DSE based data fusion
4 算例仿真与分析
4.1 基础数据与仿真条件
基于文献[27]中的IEEE-39 节点标准系统,对本文所提方法进行仿真分析,图2 为该系统拓扑结构图,图3 为某实际电网日负荷288 断面有功曲线。
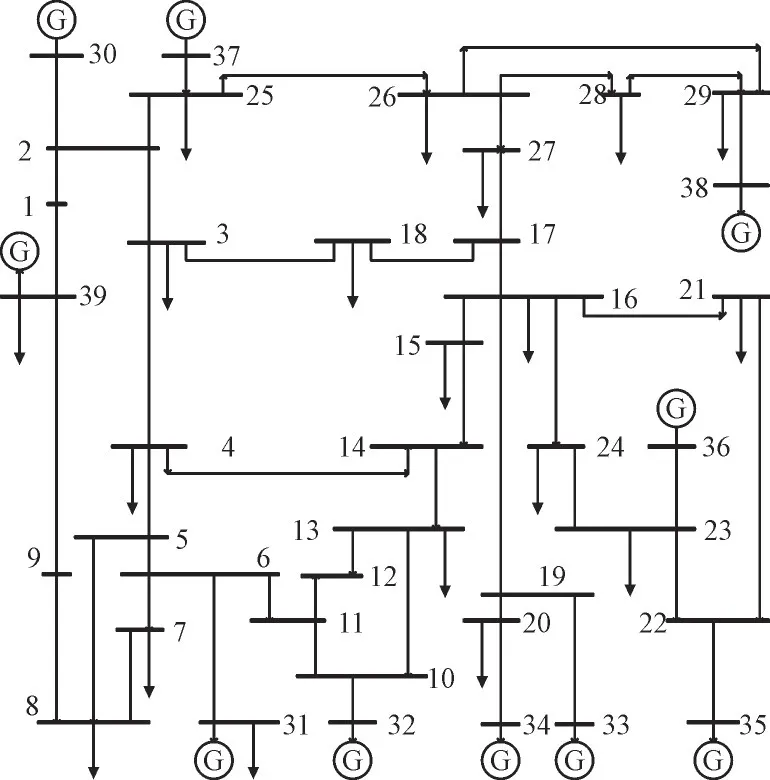
图2 IEEE-39节点标准系统结构图Fig.2 IEEE 39-node standard system structure diagram
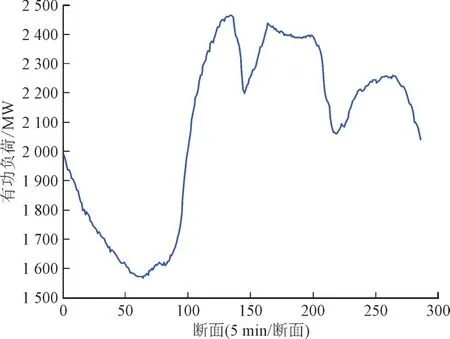
图3 某实际电网288断面日负荷曲线Fig.3 Daily load curve of 288 sections of an actual power grid
以图3 曲线在标准系统上模拟实际动态变化,在潮流真值基础上,叠加Gauss 噪声以模拟实际量测,相关仿真参数设置与文献[22]相同。
为验证本文所提基于数据融合的鲁棒动态状态估计方法的有效性,设置如下5 种仿真方案进行对比。方案一:文献[25]中普通迹卡尔曼滤波(Unscented Kalman Filter,UKF)方法;方案二:文献[26]中改进无UKF 方法;方案三:文献[27]中混合数据滤波方法;方案四:文献[27]所提两阶段鲁棒DSE方法;方案五:本文所提基于数据融合的鲁棒DSE方法。
设置如下2 种仿真条件:1)无坏数据;2)有坏数据,且坏数据的设置为令第50,70 断面10 号节点的SACDA,PMU 的电压模值测量变成100 倍。
4.2 仿真结果与分析
4.2.1 估计精度分析
使用均方根误差(Root Mean Square Error,RMSE)作为估计结果的性能评价指标,RMSE 计算式为:
式中:为k时刻第i个真值;xk,i为k时刻第i个估计值;n为状态个数;ERMS(k),ERMSmax和ERMSmean为k时刻RMSE 的值、RMSE 的最大和RMSE 的平均值;max 表示取最大值;mean 表示取均值。
对以上5 种仿真方案分别在有无坏数据情况下进行仿真,仿真结果如表1 和表2 所示。
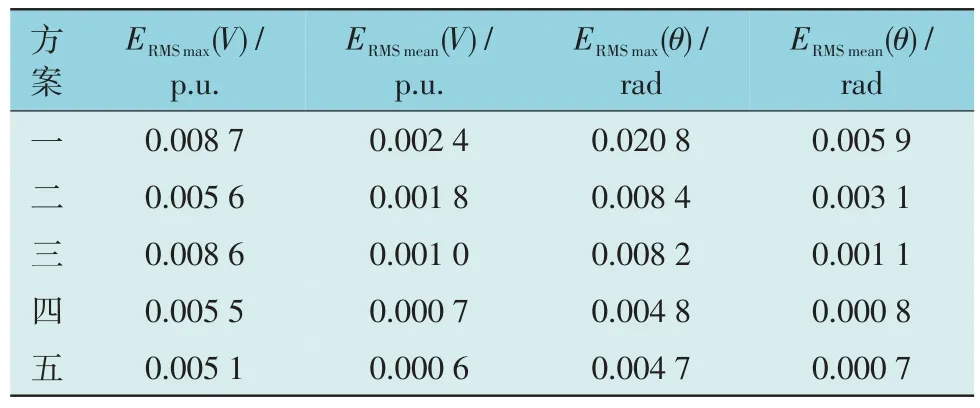
表1 无坏数据时IEEE-39节点标准系统RMSE结果Table 1 RMSE results of IEEE 39-node standard system without bad data
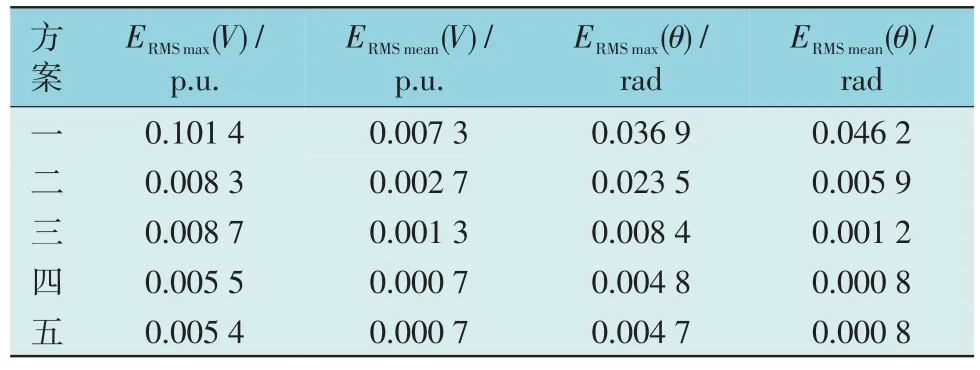
表2 有坏数据时IEEE-39节点标准系统RMSE结果Table 2 RMSE results of IEEE 39-node standard system with bad data
由表1 可知:无坏数据时,5 种仿真方案的估计结果RMSE 指标均较小,估计精度均较高,但方案四的两阶段滤波和本文所提基于数据融合理论的鲁棒DSE 方法中,最大/平均电压幅值RMSE 指标和最大/平均电压相角RMSE 指标分别为0.005 5/0.000 7 p.u.和0.004 8/0.000 8 p.u.以 及0.005 1/0.000 6 p.u.和0.004 7/0.000 7 p.u.,两者结果基本一致,且均比方案一的普通UKF、方案二的改进UKF和方案三的混合数据滤波的结果更好。主要原因在于,两阶段滤波和本文所提基于数据融合方法的并行鲁棒滤波,在每一断面进行滤波时,分别对SCADA 数据和PMU 数据单独进行滤波处理,消除了精度较低的SCADA 量测对精度较高的PMU 量测的影响。且本文所提方法在并行滤波过程中得到两组滤波结果,并将两组滤波结果采用数据融合方法得到最佳估计值,作为该断面的最终估计结果,仿真结果表明本文所提方法估计结果RMSE 指标最小,估计精度最高。
由表2 可知:有坏数据时,普通UKF 和改进UKF 的RMSE 指标相对于无数据时均有所大,鲁棒性较差。然而,方案四的两阶段滤波和本文所提基于数据融合理论的鲁棒DSE 方法的RMSE 指标相对于无数据时基本不变,鲁棒性较好。主要原因在于,两阶段滤波和本文所提基于数据融合技术的鲁棒DSE 方法在DSE 过程中,将无迹变换与指数权抗差估计结合,可对坏数据进行有效处理,鲁棒性较好。
4.2.2 计算效率分析
在无坏数据和有坏数据条件下,分别统计连续288 断面DSE 计算中混合数据滤波、两阶段滤波和本文所提基于数据融合的鲁棒DSE 方法计算时间,如表3 所示。
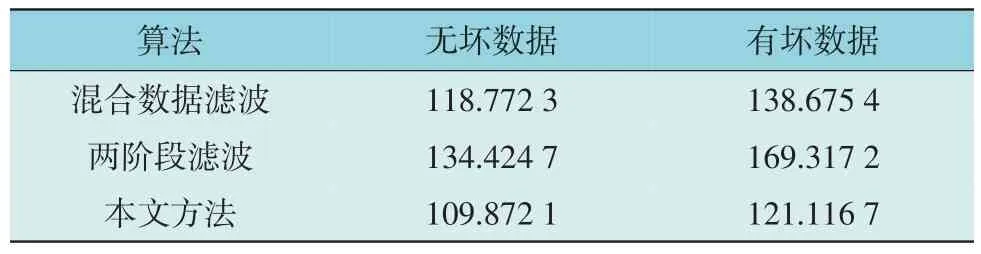
表3 IEEE-39节点标准系统288断面DSE计算时间Table 3 DSE computation time of 288 sections of IEEE 39-node standard system s
由表3 可知,在无坏数据情况下,混合数据滤波、两阶段滤波和本文所提方法的288 断面DSE 计算时间分别为118.772 3 s、134.424 7 s 和109.872 1 s;在有坏数据情况下,混合数据滤波、两阶段滤波和本文所提方法的288 断面DSE 计算时间分别为138.675 4 s、169.317 2 s 和121.116 7 s。由此可知,两阶段滤波DSE 计算所需时间最长计算效率最低,其次是混合数据滤波,而本文所提方法DSE 计算时间最短。
两阶段滤波DSE 计算在每一断面的滤波过程中,为充分利用PMU 和SCADA 数据,要进行两次滤波,故而增加了算法所用时间,计算效率较差。混合数据滤波虽只需执行1 次滤波计算,但由于将PMU 和SCADA 数据混合使用,单次计算处理量测数据量较大,雅可比矩阵计算维度较大,所需时间也仍较多,且存在SCADA 和PMU 数据相互影响的问题,降低了估计精度。本文所提方法基于数据融合理论,对PMU 和SCADA 数据分别进行并行滤波处理,在充分结合利用PMU 和SCADA 数据增大估计精度的同时,可大大增加计算效率,减少算法所用时间,有利于DSE 的实际应用。
5 结论
本文针对电力系统在连续多断面DSE 中,现有混合数据处理方法存在的两者数据相互影响以及两阶段处理方法存在的效率低下问题,提出了基于数据融合技术的电力系统鲁棒DSE 方法,该方法具有以下特点:
1)基于改进变点重复检测方法计算最优缓冲长度,将SCADA 和PMU 数据进行断面归一化处理。
2)基于数据融合理论,在每一断面分别对SCADA 和PMU 数据进行并行滤波处理,得到两组结果,并将两组滤波结果采用数据融合技术得到最佳估计值,有效避免精度较低的SCADA 数据对精度较高的PMU 数据的影响。
3)基于数据融合技术的状态融合方法,在进行并行滤波处理的同时大大提高了算法的执行效率,有利于DSE 方法的实际应用。
