支撑电网频率稳定的双馈风机一次调频控制需求分析

2023-11-10屈兴武马天诚黄云辉熊斌宇周克亮

智慧电力 2023年10期

屈兴武，王栋，马天诚，黄云辉，熊斌宇，周克亮

（水路交通控制全国重点实验室（武汉理工大学），湖北武汉 430000）

0 引言

在双碳背景下，我国风力发电技术蓬勃发展[1]。截至2023 年4 月底，我国累计风电装机容量达到3.8 亿千瓦，同比增长11.8%[2]。大规模风力发电机组替代常规火力发电机组接入电网，系统也要求其提供频率支撑能力。对此，学术界提出了减载与一次调频控制相结合的快速调频控制方案，得到广泛认可[3-5]。然而，随着大量风电机组配备调频支撑技术之后，会通过影响风机动态来改变电力系统频率动态甚至稳定特性。因此有必要对当前风电机组的调频策略和系统频率稳定需求进行适配分析。

随着双馈风力发电机（Doubly-Fed Induction Generator，DFIG）的广泛应用，其调频策略的研究较为丰富[6-8]。有研究学者提出通过下垂控制来模拟同步发电机的调差特性，当电网出现频率扰动事件时，可以提取风力发电机的备用功率，向电网提供有功支撑[9-10]。还有学者提出一种风电机组变速变桨协调减载的调频控制方法，根据减载率划分风速区间，灵活采用超速法和变桨法，确保风机保留一定备用功率，并结合附加的频率控制模块，使风电机组在调频初期提高或降低功率输出，以减小系统频率变化率和最大频率偏差[11-12]。文献[13]针对DFIG 频率问题，在功率控制环中额外附加频率控制，利用风力机存储的动能提供调频作用并参与到电网频率的恢复中。文献[14]主要研究配置了惯量控制和一次调频控制的双馈风机，使建立的模型能够脱离电网信息来反应装备的动态特性，但是未考虑电网侧特征，建立起能够反映加入调频和惯量控制之后对系统表征的物理特性。综上，当前风电机组参与一次调频的控制策略包含减载预留备用及引入调频控制提取备用功率2 个环节，但该策略更多是从装备支撑电网调频角度考虑设计的，未评估其加入对系统频率动态的影响。

当前多个并网标准，诸如《华中区域并网发电厂辅助服务管理实施细则》[15]、《并网电源一次调频技术规定及试验导则》[16]及《GB/T 19963.1-2021 风电场接入电力系统技术规定第1 部分:陆上风电》[17]，已经对风电场参与调频的响应速度及稳态精度等指标提出了量化要求。文献[18]以暂态稳定为约束条件研究系统可接纳最大风机容量，然而该方法未考虑风机机组动态。文献[19]建立了风电一次调频传递函数模型，采用解析法求解出频率约束下风电占比极限值，但建模时依旧忽略了转速及桨距角控制等动态环节，而文献[20]研究表明这些机组自身控制对风机频率响应是有显著影响。因此，对于电力系统频率特性分析而言，尚缺乏精准的含调频控制风机的建模。

本文对含调频控制的双馈风机展开分析：首先，考虑风机调桨、调速等机电控制的影响，建立了精准刻画DFIG 调频响应动态的动力学模型。继而，解析推导DFIG 一次调频、桨距角/转速控制等环节与其调频尺度等效惯量、阻尼的关联，并分析了相应控制参数的影响。最后，基于提出的风机动力学模型进一步建立了系统平均频率响应分析模型，以电网频率稳定为约束推导了对风机调频控制的量化要求。并在Matlab/Simulink 平台仿真验证了所提模型及分析方法的准确性。

1 含DFIG调频的电力系统频率响应模型构建

1.1 含DFIG调频的电力系统频率分析模型建模

在一个含有n台同步发电机（Synchronous Generator，SG）的系统中计入m台双馈风力发电机，当系统出现功率不平衡的时候，SG 的内电势频率由其摇摆方程可表示为：

式中：Δωi为SG 的内电势频率变化量，ΔPmSG_i，ΔPLSG_i，MSG_i分别为第i台同步机的输入机械功率变化量、输出电磁功率变化量和惯量；s为微分算子。

定义Meqw_j（s）为第j台双馈风机系统的等效惯量，表示为：

式中：MDFIG_j，DDFIG_j分别为第j台双馈风机的惯量和阻尼。

由于DFIG 将输入的机械功率进行了折算，DFIG 的内电势频率可以表述为：

式中：Δωj为DFIG 的内电势频率变化量；ΔPLW_j为第j台双馈风机输出的电磁功率变化量。

DFIG 和SG 在共同面对同一功率缺额ΔPL时，两者分别承担的电磁功率的等量关系为：

加入DFIG 的频率分析模型主要关注频率动态过程中的共模成分Δωˉ，即所有设备的平均频率。这样，同步机的摇摆方程和DFIG 的机械功率方程分别为：

联立式（5）—式（6）得到：

此时，由于只考虑共模的成分，可得：

定义系统的等效惯量为式（9）中的分母：

输入的机械功率近似为：

式中：Ggov_i（s）为第i台同步机调速器的传递函数。

根据式（10）推导的等效惯量，对于含DFIG 调频的系统建立各设备端口功率-频率响应关系，可得到如图1 所示的含DFIG 调频的电力系统平均频率分析模型。图1 中ΔPm为系统输入机械功率；Ggov_w（s）为DFIG 一次调频传递函数。

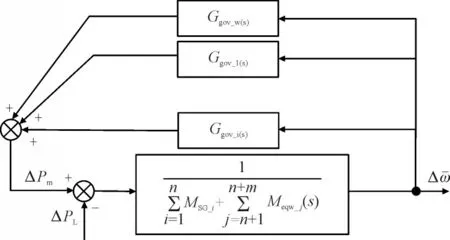
图1 含DFIG调频的电力系统平均频率分析模型Fig.1 Average frequency analysis model of power system with DFIG frequency regulation

1.2 DFIG频率响应模型建模

在含DFIG 调频系统的频率调节的过程中，风机内电势的频率Δω主要由不平衡的有功功率决定[21]，这样，简化的DFIG 频率响应模型如图2 所示，图2 中Meqw（s）为风机的等效惯量；Kf（s）为风机一次调频传递函数；Δω，Δδ分别为内电势频率和相位的微增量。

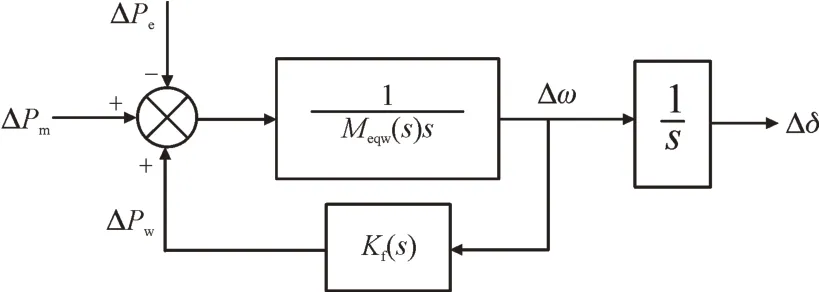
图2 简化的DFIG频率响应模型Fig.2 Simplified frequency response model of DFIG

类似于同步机，文献[22]将风机并网看做定子内电势经定子电抗接入的形式，可定义DFIG 机电时间尺度下内电势矢量为：

式中：E为d，q同步旋转坐标系下内电势矢量；ir为转子电流；Xm为定转子互感电抗。

通过定义DFIG 内电势，将风机采用的控制方式都统一转化为内电势输入输出的功率不平衡与内电势状态间的动态关系，为推导DFIG 运动方程模型，获取其等效惯量提供了基础。

2 DFIG 调桨减载一次调频系统运动方程建模

2.1 DFIG调桨减载一次调频系统运动方程建模

DFIG 机电时间尺度控制基本控制如图3 所示。

图3 DFIG机电时间尺度控制框图Fig.3 Electromechanical time scale control block diagram of DFIG

图3 中，vwind为风速，ωr，分别为转子转速及其指令值；ωPLL，θPLL，ωb分别为锁相环（Phase Locked Loop，PLL）输出角速度、相位和角速度基准值；ωw，kpp分别为叶片旋转角速度、桨距角控制器比例系数；β，βp，βpc分别为桨距角实际值、指令值、补偿指令值；，Pe，Pref分别为电磁转矩指令值、风机输出的电磁功率及其指令值，Kf，Pw分别为一次调频系数和一次调频功率补偿量；PIc，PIw，PIv分别为桨距角补偿控制器、转速控制器和端电压控制器；ir，is，ig分别为定子电流、转子电流和网侧电流；Eg，Us，Udc分别为网侧内电势、电网电压和直流母线电容电压；，分别为转子电流d，q轴分量、端电压和其指令值；Ls，Lm，ψs分别为定子等效绕组自感、定转子等效绕组之间的互感和定子磁链矢量；LPF 为低通滤波器（Low Pass Filter，LPF）；Lf为滤波电感。

在高风速时，DFIG 可采用调桨减载一次调频控制，通过减小有功功率指令值Pref来调整桨距角，使DFIG 预留有功备用。减载后，风机运行在次优功率曲线上，初始减载率为d%时，满足：

式中：Pmeas为该风速下风机最大可获取功率；Pref为风机减载运行时的有功功率指令值。

对风力机线性化可得：

式中：下标0 表示该物理量的稳态值。

对于单质量块的传动链模型进行线性化可得：

DFIG 采取调桨减载一次调频控制时，桨距角控制的输出的实际值由桨距角控制和桨距角补偿2个部分构成，皆为PI 控制，桨距角实际值可以表示为：

桨距角控制指令值为：

当系统频率变化时，一次调频控制以PLL 测量的转速与转速指令值偏差为输入，改变桨距角补偿指令值来改变桨距角控制的输出的实际值，继而调节原动机机械功率，此时桨距角补偿控制可表示为：

式中：kpc，kic为桨距角补偿控制器比例与积分系数。

对式（17）—式（20）进行线性化可得：

转速控制器可以表示为：

式中：kpw，kiw变为转速控制器比例与积分系数。

将式（22）线性化可得：

PLL 测量输入为端电压相位θt，输出测量相位θPLL，可表示为：

式中：kpPLL，kiPLL为锁相环控制器比例与积分系数。线性化可得：

式中：GPLL（s）为锁相环传递函数。

综合所有方程，可以得到DFIG 功率扰动-内电势相位/幅值的框图为如图4 所示。

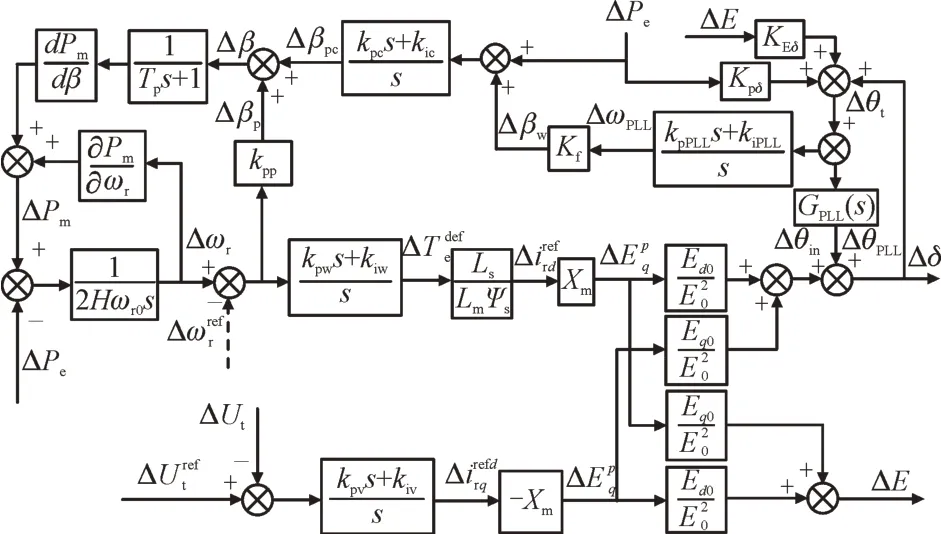
图4 DFIG桨调桨减载一次调频线性化模型Fig.4 Linearization model of primary frequency regulation of DFIG pitch load shedding

图4 中Δ代表该物理量的增量，下标含0 的表示该物理量的稳态值；上标p和下标d，q表示对应变量在锁相环旋转坐标系下的d，q轴分量；E，θin，，分别为内电势在锁相环坐标系下的幅值、相位以及d，q轴分量；kpv，kiv为端电压控制器控制系数；KEδ，KPδ分别为对应变量的传递参数；δ为风机内电势在公共坐标系下的相位；H为转子惯性时间常数；Tp为桨距角控制延迟时间常数。

由图4 线性化框图可推导出双馈风机的等效惯量用化简后的传递函数形式表示为：

风机一次调频传递函数表示为：

2.2 模型验证

为了验证建立的含DFIG 调频的系统频率动态响应分析模型的正确性和可靠性，在MATLAB 中搭建了双机系统时域仿真模型与频率动态分析模型对照，研究的模型拓扑结构如图5 所示。双机系统工况设置为Pew=0.9 p.u.，PeSG=0.55 p.u.，风机一次调频系数Kf=20，风电机组使用聚合模型。

图5 双机系统示意图Fig.5 Schematic diagram of two machine system

基于双机系统，在100 s 时在负荷上增加12.5%的阶跃扰动，得到了如图6 所示的频率动态分析模型和时域模型的频率响应曲线图。从两模型的频率响应曲线对比中可以看出，时域模型的仿真结果与所建立的频率动态分析模型的频率曲线基本一致。

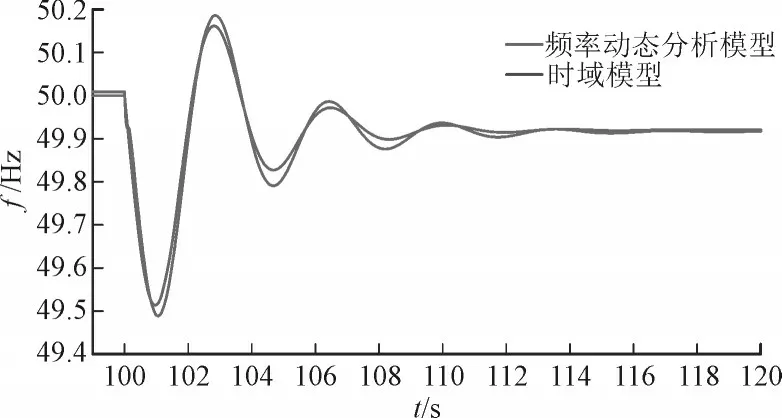
图6 频率动态分析模型与时域模型仿真验证Fig.6 Frequency response curves of frequency dynamic analysis model and time-domain model

3 DFIG 一次调频对系统频率响应特性影响分析

3.1 DFIG一次调频对系统频率响应特性影响

由式（26）得出了DFIG 调桨减载一次调频控制方式下的等效惯量频域表达式，对其进行幅频特性分析，频域下，设s=jw，风机的等效惯量可表示为：

Meqw在虚轴上投影的长短（虚部）反映了阻尼的强弱，在正阻尼区，投影越长风机调频控制环节提供的正阻尼越强，对系统稳定更有利，反之则不利；类似地，Meqw在实轴上投影的长短（实部）反映了惯量的大小。因此，通过分析等效惯量Meqw的实部和虚部，可以近似量化风机的惯量和阻尼大小，进而解释DFIG 不同控制环节对系统频率动态的影响。

图7 为改变不同控制环节下风机等效惯量变化伯德图。

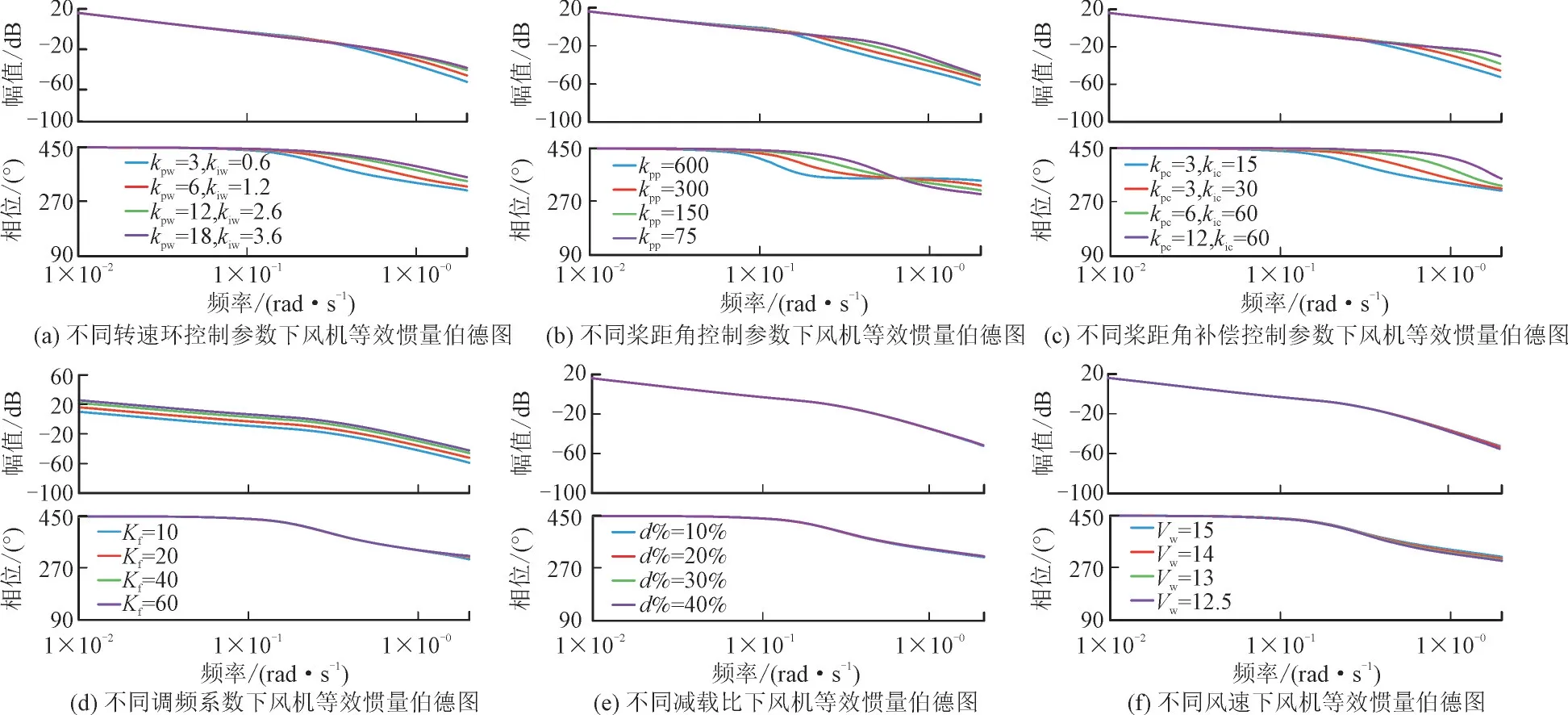
图7 改变不同控制环节下风机等效惯量变化伯德图Fig.7 Bode diagram of equivalent inertia change of DFIG under different control links

图7（a）给出了风速15 m/s 下，风机转速环PI控制控制增益在kpw=3，kiw=0.6 基础上倍增1～4 倍风机等效惯量的伯德图，可以看出随着转速控制增益变大，低频段，即频率响应模式振荡区间，惯量增益也变大，说明一定程度上可以提高风机惯量水平。同时在也逐渐接近360°方向，说明风机提供的负阻尼也在增加。

类似地，图7（b）为桨距角控制增益变化时风机等效惯量的伯德图，随着桨距角增益变大，风机惯量增益变化不大，但是在低频振荡区间阻尼增大。图7（c）为桨距角补偿控制增益变化时风机等效惯量的伯德图，可以看出桨距角补偿控制增益变大，惯量会增大，同时低频振荡频段的负阻尼增大。图7（d）为调频系数对风机等效惯量影响的伯德图，可以直观看出，调频系数越大，风机惯量增大。图7（e）为风机不同预留备用时等效惯量的伯德图，可以看出在满足调频容量的前提下，改变减载比对风机等效惯量影响几乎可以忽略。图7（f）为高风速时不同风速下风机等效惯量的伯德图，由于风机转速已达到额定值，稳态功率达到最大值，可知风机运行在高风速时风速变化对系统惯量和阻尼的影响较小。

3.2 时域仿真验证

图8 为改变风机不同控制环节时系统的频率响应图。图8（a）为不同转速控制下系统频率的时域仿真波形，可以看出转速控制增益变大，频率最低点略有上升，说明了风机惯量的增大。此外，系统低频段的振荡也在加剧，这是由于风机提供了更多的负阻尼，该时域仿真现象同频率的惯量分析结果一致。

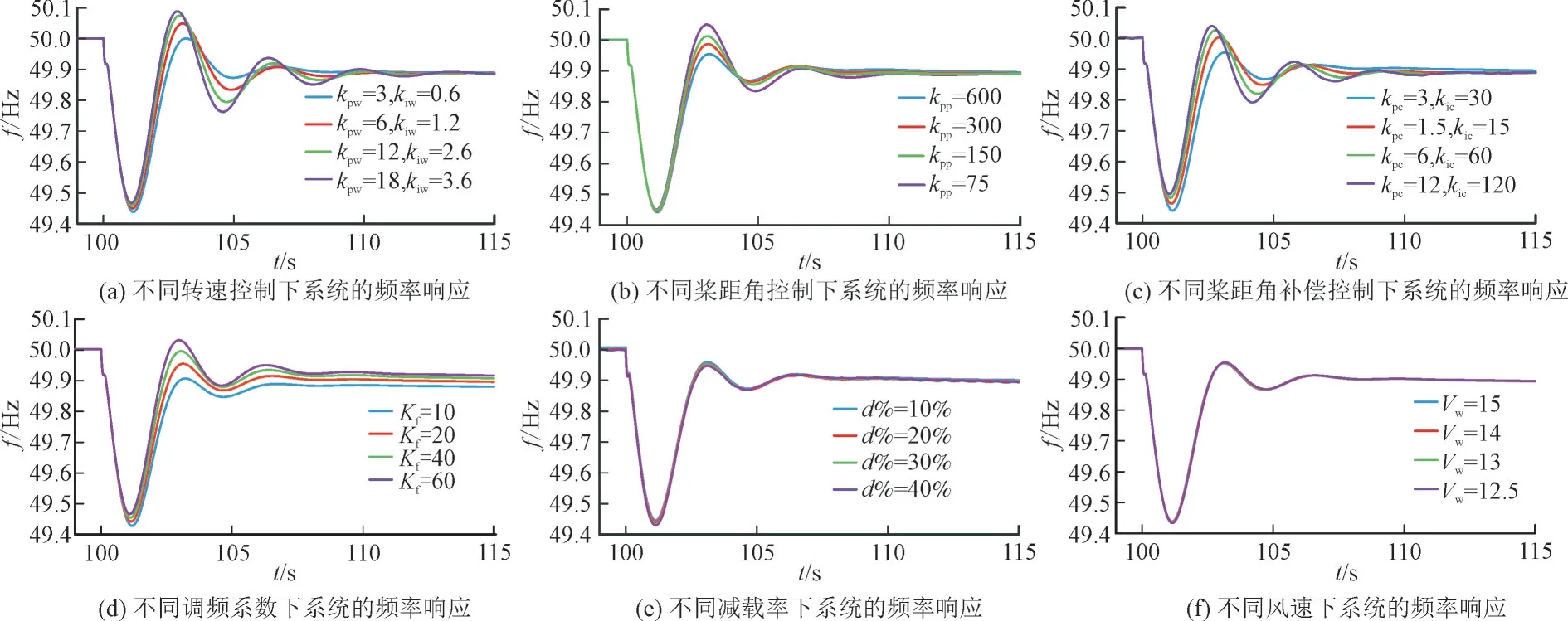
图8 改变风机不同控制环节时系统的频率响应Fig.8 Frequency response of system when changing different control links of DFIG

类似地，图8（b）为不同桨距角控制参数对应时域仿真波形，可以看出桨距角控制对频率跌落最低点影响较小，但增大控制增益有利于低频振荡的衰减，说明系统的阻尼在增大。图8（c）为不同桨距角补偿控制下系统频率的仿真波形，可以看出频率最低点减小，可见风机惯量在增大。但是系统振荡阻尼也在变小，振荡变得更为严重。图8（d）为不同调频系数下系统频率的仿真波形，可以看出，调频系数越大，风机惯量增大，同时，增大一次调频系数能提升频率跌落最低点，但系统的阻尼有所减小，振荡变得更加剧烈。图8（e）为不同减载率下系统频率的仿真波形，可以看出改变减载比几乎不影响系统的频率动态响应特性。图8（f）为不同风速下系统频率的时域仿真波形，可以看出高风速时风速变化对系统运行点影响较小，因此对系统频率动态几乎没有影响。时域仿真现象同频率的惯量分析结果一致，验证了图7 中所得结论。

4 满足电网频率约束的DFIG一次调频控制需求分析

4.1 理论约束分析

稳态频率偏差是指电力系统长时间运行时频率相对于标准频率的偏离程度，超过一定限度的频率偏差会引发电力系统不稳定、电力质量等问题。我国电力系统的正常频率偏差允许值为±0.2 Hz[23]。频率变化率（Rate of Change of Frequency，ROCOF）是评估电力系统稳定性的重要指标，我国电力系统的频率变化率限制为每分钟不超过0.2 Hz/s[24]。基于以上系统频率响应标准（稳态频率偏差和频率变化率）的限制，本节计算中，将频率偏差限定为0.2 Hz 以内，频率变化率边界可限定为0.5 Hz/s 以内。

考虑负荷功率为阶跃扰动时，时域扰动功率ΔPL与频域扰动功率ΔPd的数学关系为：

式中：ΔPL，ΔPd分别为时域下和频域下的扰动功率；SN为系统容量；s 为微分算子。

同时，依据图1 中的含DFIG 调频的系统频率响应分析模型可以得到系统稳态频率偏差的解析表达：

根据终值定理以及初值定理关系：

式中：f(t)为时域下的函数；F(s)为频域下的函数。

可以计算得到大扰动条件下，风电机组频率响应的瞬时变化率和最终稳态值可以表示为：

式中：ROCOFmax为系统的频率变化率；Δf为稳态频率偏差。

考虑到系统稳态频率偏差和频率变化率约束对DFIG 调频的要求，结合式（31）、式（34）和式（35）之间的关系，可以求取给定场景下对DFIG 调频如下垂系数、最小备用容量等的技术要求。

4.2 算例验证

本节将以典型频率大扰动事件下系统频率响应标准（稳态频率偏差、频率变化率等）为约束，从调频系数、最小调频备用容量、风机渗透率等多个角度，对调桨减载方式下的风电机组的一次调频技术要求进行研究，研究的模型结构如图9 所示。

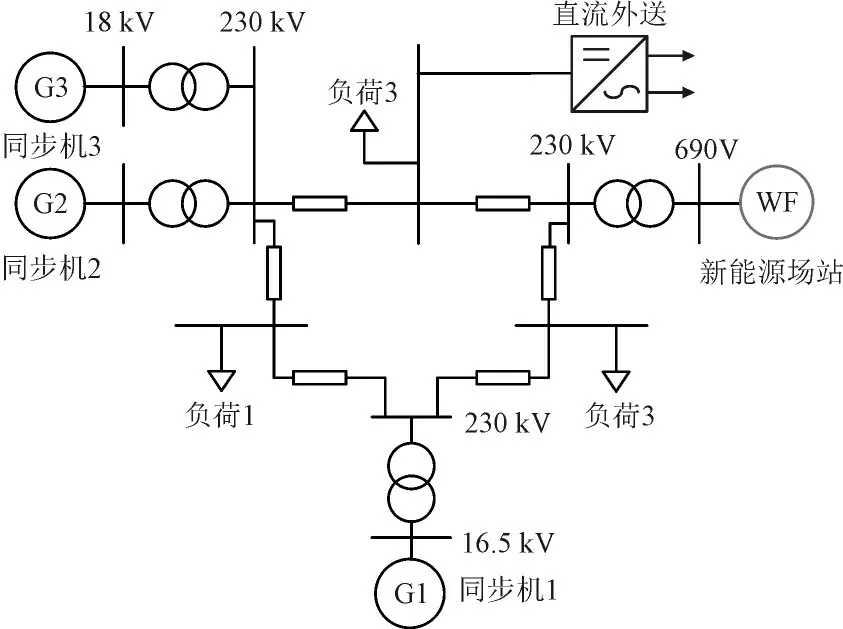
图9 拓展的三机九节点电力系统示意图Fig.9 Schematic diagram of expanded three machine nine-node power system

其中同步机1为容量为247.5MW，出力37.62MW，同步机2 和同步机3 的容量都为192 MW，同步机2 出力57.6 MW，同步机3 出力76.8 MW，风机容量为129 MW，设定减载比为0.1。风机出力116 MW，初始渗透率16.96%。

1）Case1：不加入调频控制，一定负荷扰动下保证频率动态要求风电机组的最大渗透率。

100 s 时，给定负荷突增50/760.5（dPd/SN占比），改变系统风机渗透率，得到在负荷扰动一定时的临界风机渗透率能够使系统的频率偏差满足Δf＜0.2 Hz的频率偏差标准。通过式（34）—式（35）的理论计算原理可以得到理论的临界风机渗透率为21.35%，不同风机渗透率下同步机G2 出口的频率变化波形如图10 所示。

图10 不同风机渗透率时同步机G2出口的频率响应Fig.10 Frequency response of G2 outlet of synchronous machines with different wind turbine penetrations

由图10 可知，实际风机仿真所测得的临界风机渗透率为21.95%，当系统风电渗透率降低时，系统的频率偏差将小于0.2 Hz，当渗透率进一步升高时系统的频率偏差将超过0.2 Hz，不满足电网运行标准。同样可以观察到的风机渗透率升高之后系统的频率振荡逐渐变大。由此可以由此得到在一定负荷下的风机最大渗透率约为21.35%。

2）Case2：风电机组采用调桨减载方式时，在负荷扰动突增下的最小调频系数和最小备用容量。

100 s 时，给定负荷突增dPd/SN=60/760.5，改变调频控制的调频系数，可得出让系统频率偏差Δf＜0.2 Hz 的调频系数范围、临界值、和风机在以上设定能够满足电网运行标准的最小的备用容量。时域仿真中同步机G2 出口频率变化如图11 所示。

图11 100 s时负荷扰动突增同步机G2出口频率响应Fig.11 Frequency response of G2 outlet for a sudden load increase at 100 seconds

当不加入一次调频时频率响应为图11 所示蓝色曲线，通过测量得到扰动初始时刻频率变化率最大值为0.347 8 Hz/s，通过式（34）—式（35）计算出此时理论频率变化率应为0.343 0 Hz/s，和仿真实际值基本吻合。未加入调频时稳态频率偏差0.24 Hz，超过了Δf＜0.2 Hz 的频率偏差标准。加入一次调频之后，系统有功功率增加频率偏差减小。且当Kf系数越大效果越明显。当时域Kf=20 时达到临界，能够让系统频率偏差达到Δf=0.2 Hz 的标准。通过式（34）—式（35）理论计算临界值为18，和时域仿真基本符合。即最小调频系数为Kf=20，此时可以计算出最小调频备用容量为10.32 MW。

3）Case3：风电机组采用调桨减载方式时，在系统有功负荷突减下的最小调频系数。

考虑到电网频率约束包括上下边界，100 s 时，给定负荷突减dPd/SN=60/760.5，改变调频控制的调频系数，可得出让系统频率正偏差Δf＜0.2 Hz 的调频系数范围和临界值。时域仿真中同步机G2 出口频率变化如图12 所示。

图12 100 s时负荷扰动突减同步机G2出口频率响应Fig.12 Frequency response of G2 outlet for a sudden load reduction at 100 seconds

不加入一次调频的频率响应仿真结果如图12中的蓝色曲线，通过测量得到其扰动初始时刻频率变化率最大值为0.347 0 Hz/s，通过式（34）—式（35）计算出此时频率变化率应为0.344 5 Hz/s，和仿真实际值基本吻合，验证了风电机组频率响应瞬时变化率计算的准确性。

此外，由图12 可以看出，未加入调频时稳态频率正偏差约为0.24 Hz，超过了Δf＜0.2 Hz 的频率偏差标准。加入一次调频之后，风电输出减少，调频备用容量增加，系统频率偏差减小，且当Kf系数越大效果越明显，当时域Kf=20 时达到临界，能够刚好让系统频率偏差达到Δf=0.2 Hz 的标准。通过式（34）—式（35）理论计算临界值为18.2，和时域仿真基本符合。即最小调频系数为Kf=20。