基于“认知结构”发展的数学教学分析
——以“数列通项公式”解题模块的组建与应用为例
2023-11-10江苏省宜兴市第二高级中学杨晶晶
江苏省宜兴市第二高级中学 杨晶晶
认知心理学研究发现:学习过程实则为不断构建与完善认知结构的过程,认知结构对数学教学有着至关重要的影响.奥苏贝尔提出:认知结构是指学生头脑中的知识结构,从广义的角度来看,它指一种观念的全部内容;从狭义的角度来看,认知结构是学习者在某一特定领域的观念或组织.解题模块属于重要的认知结构,对学生的解题能力发展具有直接影响.
1 组建解题模块
教学中,常会遇到这样一种现象:教师反复强调并讲了几遍的内容,学生却屡屡出错;还有一些学生课堂上能够对答如流,课后作业却漏洞百出.出现这些现象的主要原因就在于学生并没有将新知纳入到自己的认知结构中,还没有形成良好的解题模块.研究发现,解题模块能将某些杂乱无章的解题过程变得有法可依、有据可循,降低解题的难度.
要求解数列问题,首先就要对这部分知识结构有一个明确的认识.应将教材中与数列通项公式相关的知识罗列到一起,再分门别类地进行归纳,这样在解题时就能够从中探寻出相应的方法.
数列通项公式的相关问题,若题干条件中不存在递推公式,可将它分为“通过列举数字、图形与图象表示”“已知数列的某几项的值”“已知某个数列的前几项和与值”三类;若题干条件中存在递推公式,可分为多类情况(见图1).
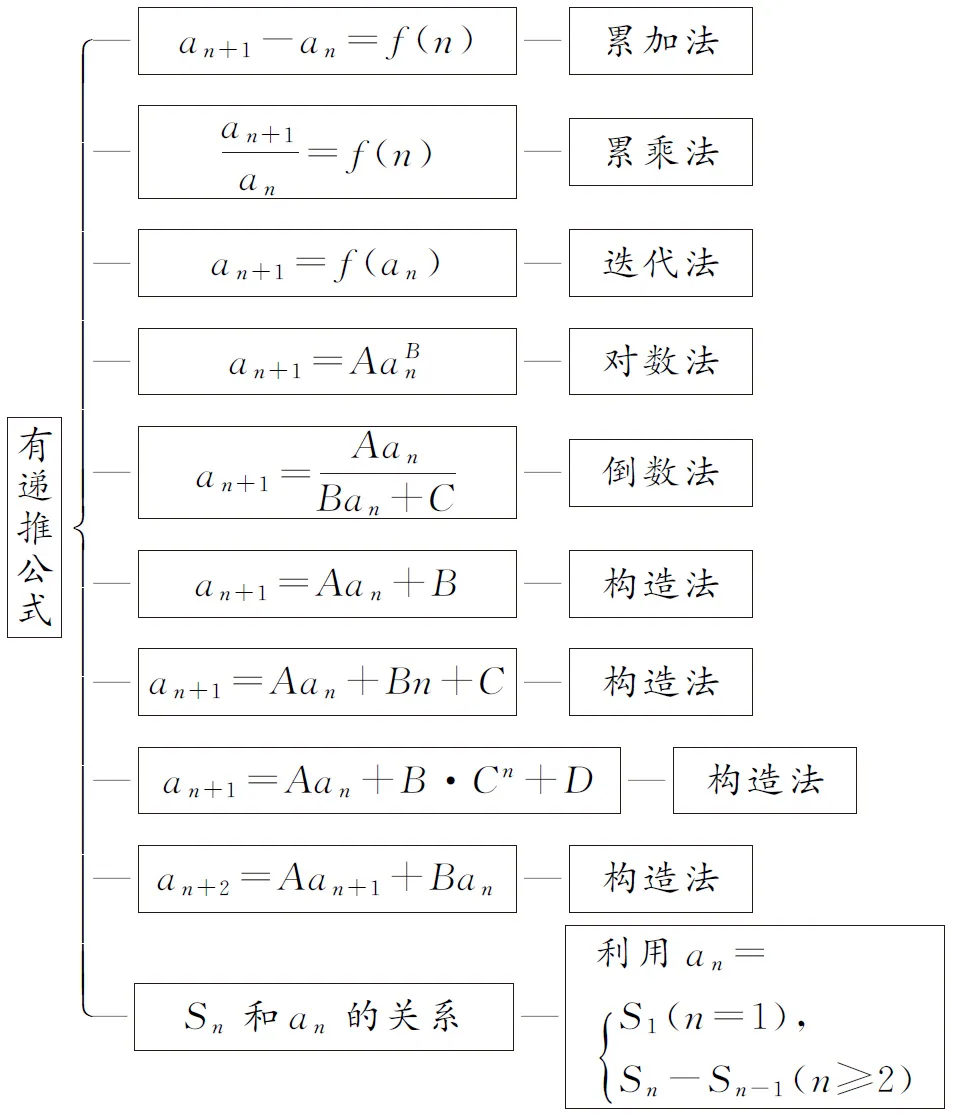
图1
一般情况下,解决无递推公式的数列问题,可应用公式法与观察法,这类问题的难度系数偏小,比较容易获得结论;而有递推公式的数列问题类型多样且灵活,高中阶段常接触到的有图1中的十类情况,且每一类情况都存在相对应的解法.这就组成了解数列通项公式的解题模块,模块的形成为解决相应的问题提供了帮助.
2 应用解题模块
张景中院士对于解数学问题提出了如下看法:无招胜有招是练武的最高境界,但练武依然需要从一招一式开始,解数学问题亦如此,都要通过一点一滴的训练与建构,才能达到“无招胜有招”的境界.对于大部分学生而言,需要充分重视变式训练,学会将数学问题分门别类,以探寻出可机械执行的巧法,也就是算法.
由此可以看出,组建解题模块是实施快速解题的上上之策,即帮助学生在脑海中建构解决一类问题的认知结构.实施解题存在多种方法,如将题干中一些隐性的条件显露出来,将一些杂乱无章、冗长繁杂的解答过程变得条理清晰、简洁明了等,可从最大程度上降低解题的难度.
(1)无递推公式类
例1已知等比数列{an}中的a1,a2,a3分别为表1第一、二、三行中的某个数,并且a1,a2,a3中的任何两个数不处于同一列,求该数列的通项公式.

表1
观察发现,本题并未给出递推公式,而且以图表法展示题干,对应解题模块可通过“观察法”来探寻数字间所存在的规律.
解:当a1=3时,与题意不符;当a1=2时,有且仅有a2=6,a3=18,与题意相符;当a1=10时,与题意不符.由此可以确定a1=2,a2=6,a3=18,那么等比数列{an}的公比q=3,其通项公式为an=2·3n-1.
(2)有递推公式,如an+1=Aan+B·Cn+D类型
例2已知数列{an}中的a1=1,an+1=2an+3n+1,求该数列的通项公式.
分析:题干有递推公式,且属于an+1=Aan+B·Cn+D型,对照图1的解题模块,可以考虑应用构造法实施解题.具体解法如下.
解法1:设存在实数λ,使得an+1+λ·3n+1=2(an+λ·3n),即an+1=2an-λ·3n,计算得λ=-3,那么an+1-3n+2=2(an-3n+1).令bn=an-3n+1,则由a1=1可知数列{bn}为一个等比数列,其首项为-8,公比为2,因此可获得数列{an}的通项公式为an=3n+1-2n+2.
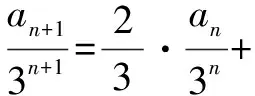
例3(1)定义首项为1,公比为正数的等比数列是“M-数列”.{an}(n∈N*)为等比数列,且满足a3-4a2+4a1=0,a2a4=a5,请证明:数列{an}为“M-数列”.

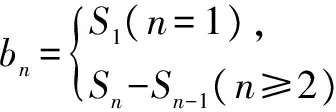
解:(1)证明略.
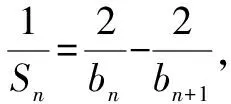
3 注意事项
3.1 理解解题模块是应用的前提
应用解题模块实施解题,并不是所有的问题都能够归结到相应的类型.如一些开放题或证明题等,并没有通用通法可以直接套用.教师不能直接带领学生识记解题模块,而应与学生一起探索解题模块形成的前因后果,让学生对解题模块的形成过程、蕴含的数学思想方法等有一定的了解,在此基础上再进行记忆与应用.
3.2 联系实例记忆解题模块
一个完整的解题模块应包含有利于学生理解的具体实例,以便于学生记忆与应用.这里所提到的实例必须具有典型性与代表性,当学生遇到与之类似的问题时,能够从解题模块中的典例着手分析,实现知识的正迁移,提高解题能力.
3.3 在“通法”的基础上补充“巧法”
解题模块作为解题的通性通法确实能有效提高解题效率,而“通法”的应用并不排斥其他新的更巧妙的方法的应用.应用解题模块进行解题教学的过程中,适当地补充一些更巧妙的方法,还能进一步发展学生的数学思维,完善学生的认知结构.
达尔文认为:与方法相关的知识是最有价值的知识.师生通过解题训练总结解题经验方法的过程中,可有针对性地完善不同题型与类别的解题模块,以促使知识的正迁移,让学生能更快、更准地将解题模块应用在实际解题中.
事实证明,解题模块的引入与应用不仅提高了学生的解题能力,还有效促进了学生反思习惯的形成.当学生面对一些错题时,会不由自主地探寻问题所归属的类别,并想方设法来解决它,甚至有学生会自主创建出新的解题模块,形成良好的认知结构.
