基于高中数学思维能力培养的“全景式”数学问题设计研究*

山东省桓台第一中学 苏同安 李晓玲

基于高中数学思维能力培养的“全景式”数学问题设计的研究,是针对高中数学各章节内容,研究设计出体现知识性质、思想方法、思维过程之全景的“全景式数学问题”(简称“一题释全景”).旨在用“全景问题”解决“题海战术”带来的弊端,减轻师生负担,提高学生学习兴趣和教学效率效果,从而全面有效地培养学生的数学思维能力,促进各层面学生核心素养的提升和全面成长;同时,也为相关的教育教学理论落实运用提供“载体”支持.

1 全景式数学问题的概念

(1)全景

全景是指所涉及内容的基本知识性质、基本问题类型、基本思想方法、动态思维过程的全部或问题由易到难、层层递进的结构全貌.

(2)全景式数学问题

全景式问题是针对某阶段(本研究是高中阶段)的数学各章节内容,能体现“知识问题、思想方法、思维过程”的全景且由易到难、层层递进的“一道题”或“一个系列问题”,简称“一题释全景”.

有的全景问题主要体现该章节的知识性质或问题类型的全景,有的主要体现思想方法或思维过程的全景,有的则兼而有之.教学中应根据各章节内容特点及关系研究设计全景问题,考虑是需要一个全景问题,还是需要多个或一系列全景问题来逐步体现各类全景.

2 全景式数学问题设计的意义

全景式数学问题设计的意义如下:

(1)培养数学思维能力,提升数学核心素养.

(2)优化数学思维品质,突破数学思维障碍.

(3)研创理论运用载体,支持相关方略落实.

(4)破解数学题海战术,减轻师生教学负担.

(5)激发学生学习兴趣,提高学生学习效率.

(6)满足各层学生需求,提升学生学习效果.

(7)提高教师研创能力,助推教师专业成长.

3 全景式数学问题设计的原则

(1)科学性

全景问题的设计,要遵循教育教学的科学规律,以相应的教育理论为指导,以高中数学课程标准为依据,运用科学合理的思想和方法;要充分体现高中数学教学的基本理念和内容目标,注重培养数学思维能力,提升数学核心素养;要符合高中学生的认知特点,有利于学生的成长和发展.

(2)全面性

《普通高中数学课程标准(2017年版)》的基本理念中要求:高中数学课程要面向全体学生,实现“人人都能获得良好的数学教育,不同的人在数学上得到不同的发展”[1].

全景问题设计的“全面性”包括三个方面:一是针对所有学生,促进各层面学生全面成长;二是问题要全面,各章节都要设计出全景问题;三是问题要体现以上所述的全景.

(3)层次性

全景问题设计的“层次性”体现在三个方面:一是适合各层面学生的学习和探究,体现“最近发展区”等相关理论的有效落实运用;二是问题难易的层层递进;三是数学思维的层层递进.全景问题既可展现知识性质、思想方法的逐步生成和逐层联系,体现知识性质、思想方法之全景,又可基于当前问题,进行追根求源、纵横拓展的全面学习和逐步思悟,体现思维过程之全景.

(4)多元性

人们的数学思维方式和智能都是“多元”的,而且数学思维能力是数学核心素养的具体体现.比如,“抽象概括思维能力”可体现“数学抽象”核心素养;“逻辑思维能力”可体现“逻辑推理”核心素养;“形象思维能力”及“空间想象能力”可体现“直观想象”核心素养;“数学运算能力”可体现“数学运算”核心素养;等等.数学核心素养、数学思维能力的提升和多元智能的全面发展是一个不可分割的有机整体,全景问题的设计应满足这个整体的提升和发展.

(5)探究性

“数学问题”是培养学生素养与能力的重要“载体”.利用数学问题进行学习思考的本质就是一种重要的、有意义的数学探究活动.探究活动的质量不在于“题量”的多少,关键在于激发学生的探究愿望以及“思维量”的大小,所以设计的全景问题,要能充分体现激发学生“思维量”的探究性过程.

(6)创新性

全景问题设计要在体现教材的基本内容、要求的基础上,渗透“大单元教学理念”,体现问题模式的创新.同时为相关教育理论方略的落实提供全面的课程资源支持,在理论方面体现出创新性.

实践方面的创新性.可解决“题海战术”带来的弊端,提高学生学习兴趣和效率,减轻师生负担,全面有效地培养学生的数学思维能力[2].

4 全景式数学问题设计的策略

(1)设计“知识问题”方面的全景问题,体现数学思维全面性的培养

《普通高中数学课程标准(2017年版)》的基本理念中,特别强调了提升、发展学生“数学学科核心素养”的重要性.

数学思维能力是对数学学科核心素养所包含的六个维度要求的具体体现,并形成一个有机整体,教学中应注重数学思维能力的全面培养,不能追求片面.

设计“知识问题”方面的全景问题,融入数学思维这个有机整体,全面体现出对逻辑推理能力、抽象概括能力、空间想象能力、数学运算能力等数学思维能力的培养,助推学生数学思维品质的全面提升.

(2)设计“思想方法”方面的全景问题,体现数学思维灵活性的培养

数学思维的灵活性是指能根据客观条件或事物的发展变化,善于多方位思考,及时恰当转变思维方向、摆脱思维定式,提出解决问题的新方略或寻找新的解题途径.体现出从不同角度、方面,用多种方法来分析、解决问题的能力[3].

数学思维的灵活性占据数学思维品质的重要位置,体现数学思维能力培养和灵活运用知识分析问题、解决问题的情况,对其培养非常重要.

设计“思想方法”方面的全景问题,可培养学生的数学思维能力,提升数学思维灵活性的品质.

(3)设计“思维过程”方面的全景问题,体现数学思维深刻性的培养

数学思维的深刻性是指思维活动的抽象程度和逻辑水平,以及思维活动的广度、深度和难度.体现把握问题本质,对数学问题进行追根求源、纵横拓展的思维能力,并在此基础上进行探索创新的能力.

数学思维的深刻性占据数学思维品质的核心位置,体现透过现象看本质及举一反三、触类旁通的思维水平.对数学思维深刻性进行培养非常重要.

设计“思维过程”方面的全景问题,可培养学生的数学思维能力,提升数学思维深刻性的品质.

说明：由于数学思维的各种品质是一个有机的整体,因此设计全景问题,对思维的灵活性、深刻性进行培养,定会同步提升其他的思维品质,如思维的发散性、敏捷性、创新性及批判性.上文只是以思维的灵活性、深刻性为重点进行分析说明.

5 高中数学全景问题设计举例及设计说明

针对高中数学各章节内容,依据全景问题设计模式,设计出对应的全景式问题.下面以立体几何为例,设计一个立体几何全景问题,并给出设计说明.

5.1 全景式问题案例

如图1,四边形ABCD是直角梯形,CD⊥BC,且AD∥BC,BC=2AD;四边形BCEG是梯形,且BG∥CE,CE=2BG;四边形DCEF是平行四边形.

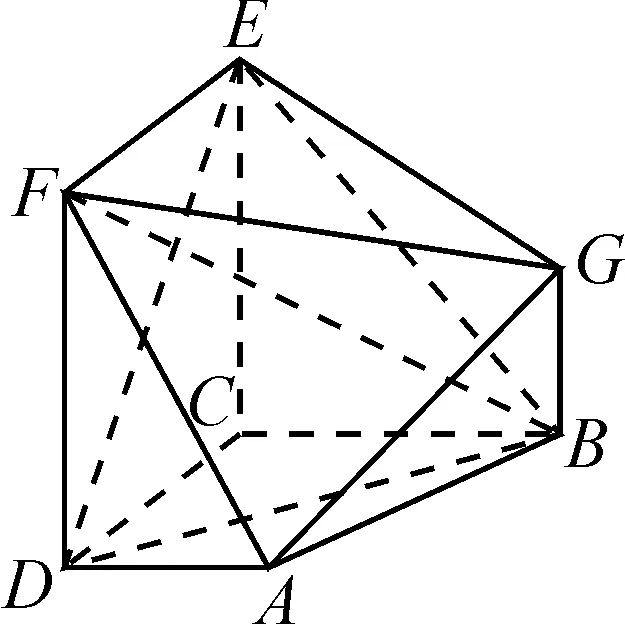
图1

(1)求证:AG∥平面BDE.

(2)若BE=4BG,且∠EBG=60°,求证:平面DCEF⊥平面ABCD.

(3)在(2)的条件下,FB⊥DE,∠FDC=60°.求AG与平面BEF所成角的正弦值和二面角B-EF-D的余弦值.

(4)在(3)的条件下,线段AG上是否存在一点M,使得CM∥平面EFG?若存在,确定M的位置;若不存在,请说明理由.

(6)在(5)的条件下,且BG=1.若N是线段BE上一点,且二面角N-AC-B的大小为30°,试确定点N的位置,并求点N到平面FCB的距离及三棱锥N-FCB的体积.

(7)在(6)的条件下,若P是直线EF上的点,求EA与平面PBC所成角正切值的最大值;若P是以DC,DA,DF分别为长、宽、高的长方体棱上的一点,且满足|PD|+|PE|=m(m>0)的点P的个数为4,求m的取值范围.

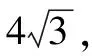
(9)在(6)的条件下,取BC中点Q,动点W在以CD为底面半径的圆锥BC的底面内(包括圆周),若DQ⊥WQ,求点W形成的轨迹长度;取BD中点S,求四面体EBCS外接球的体积及该球被几何体的面ABCD,CDFE所截得的圆弧长之比;取CE中点T,若四面体TBCS内切球的内接圆锥(其高过球心)与内接正三棱柱的底面在同一平面内,求该圆锥的侧面积与该正三棱柱的体积之比的最小值.

5.2 案例设计说明

该全景问题,以一个可变的“组合体”为载体,以两条互融的“知识线”为导向,自然融合了点、线、面、体等的知识性质,动态展现了它们之间的各种关系及演变,形成知识性质全景,并层层递进演变出问题类型全景,进而诠释出思想方法、思维过程全景.

主线之一是重要的“平面图形”与“点、线、面”的融合及关系演变.问题中的“四边形EFDC”随着问题的层层推进逐步演变为平行四边形、菱形、矩形、正方形等各种四边形;另一重要图形“梯形ABCD”也相伴同行;直线CE与平面ABCD、平面EFDC与平面ABCD的关系也随之形成“从不垂直到垂直的演变”.各要素演变与线线、线面、面面关系及演变密切相连.

主线之二是重要的“几何体”与“点、线、面”的融合及关系演变.在重要的平面图形与点线面关系的支持下,逐步演变出棱锥、棱柱、圆锥、球等重要几何体及相关几何体的“接切”关系,相关的重要元素如体积、面积、圆弧、侧棱也相伴相随.对这些重要元素的研究与求解,与点、线、面关系中的“距离”“角度”等重要量又紧密相连、不可分割.

(1)建构知识问题全景,体现思维全面性的培养

问题类型全景与知识性质全景同行,既有判断、论证各种关系的基本问题,又有利用各种关系进行综合性推理论证的问题;既有关于距离、角、面积、体积等重要量的运算求解问题,又有关于距离、角、面积、体积等要素的范围最值的探究性问题;既有“正向型”典型问题,又有“逆向型”开放问题.这些问题不仅包含立体几何各要素,还与代数要素产生密切联系.

问题(1)与(2),是关于“平行垂直”的正向推理论证的基本问题,问题(3)～(5)是关于“平行垂直”的逆向推理运用与“异面角”“线面角”“二面角”的运算求解相融合的问题,证中有算,算中有证,充分体现出对逻辑推理、数学运算、空间想象等能力的全面培养;综合问题(6)～(9),逐步融入多面体与旋转体,加入关于距离、长度、面积、体积等元素的分析计算和相关量最值范围的推演探究,在培养逻辑推理、数学运算、空间想象等能力的基础上,体现对抽象概括能力、数据分析能力的培养,助推数学思维品质的全面提升.

(2)融入思想方法全景,体现思维灵活性的培养

该全景问题,以全面丰富、包容开放的背景和设问,融入了数学思想方法的全景,体现出对数学思想方法的对比选择和全面思悟.

问题(1)的论证,线线平行法、面面平行法、向量法均可体现,各方法中还有不同思路的选择;问题(2)中的垂直论证,可融入“算”的方法;问题(3)～(5)的解决,则是“几何推演”与“向量运算”两种主要思想方法的碰撞与融合;问题(6)～(9)中关于最值范围的问题,更是与函数、三角、不等式,甚至是圆锥曲线等数学核心知识相结合,广泛体现了等价转化、函数与方程、数形结合等数学主要思想方法的运用及本质联系.

此全景问题,可体现从不同角度用多种方法或选择恰当方法分析解决问题的能力,助力突破思维定式障碍,提升数学思维灵活性的品质.

(3)生成思维过程全景,体现思维深刻性的培养

“思维量”比“题量”更重要,由可变组合体和两条互融的知识线及问题与方法的全景,可体悟到全景问题设计注重数学思维的生成过程,关注数学思维的逻辑性、连续性和递进性.

问题(7)中求m的范围问题,既可看作从三维空间到二维平面的追根求源,又可纵横拓展将问题一般化、抽象化,总结规律方法,还可与代数、三角产生联系,展现数学知识的广泛联系和本质内涵,体现数学思维及思想方法的广泛性、灵活性和深刻性.

该全景问题,能够让学习者对立体几何、空间向量及相关的数学知识性质、思想方法,有一个全景式思悟和全面深刻的理解把握,进而做到举一反三、熟练灵活运用,推动数学思维走向广泛和深刻.