“二元一次不等式确定平面区域”方法的优化探究

江苏省苏州市田家炳实验高级中学 邓志敏 江苏省苏州市桃坞高级中学 缪诣欣

1 对教材意义的认识

“简单的线性规划问题”是数学实际应用的典范,是培养学生“数学建模”思想和能力的重要理想素材.对于高中学子而言,简单的二元变量线性规划问题贴近生活实际,让他们觉得数学“并不遥远”.而且,高中阶段“线性规划”问题一般涉及在一定条件下合理配置资源,为使某种目的达到最佳,统筹人力、物力等作出最优决策而提供数学解决依据.因此,该学习内容能够激发学生学习数学的兴趣,提高运用所学知识解决实际问题的积极性,并在问题解决中获得“成功体验”.该内容能进一步加深学生对“函数”的理解,多角度锻炼学生“数形结合”能力,培养学生“应用数学”意识,是增强学生分析、解决问题能力的良好载体[1].

2 问题的提出、解决及结论的推广

2.1 问题的提出

关于二元一次不等式(组)所表示的平面区域的确定,以Ax+By+C>0或Ax+By+C<0,A2+B2≠0为例,一般有以下三种方法:

(1)取点判别法:直线定边界,一点定区域,“合则在,不合则不在”.

(2)B符号判别法:直线定边界,符号定区域,“同上异下”.

(3)A符号判别法:直线定边界,符号定区域,“同右异左”.

其中后两种判别法具体叙述如下:已知二元一次函数f(x,y)=Ax+By+C(A2+B2≠0).

①B符号判别法:若B≠0,则有点P1(x1,y1)在直线Ax+By+C=0上方⟺B与f(x1,y1)同号;点P1(x1,y1)在直线Ax+By+C=0下方⟺B与f(x1,y1)异号.

②A符号判别法:若A≠0,则有点P1(x1,y1)在直线Ax+By+C=0右侧⟺A与f(x1,y1)同号;点P1(x1,y1)在直线Ax+By+C=0左侧⟺A与f(x1,y1)异号.

良好的教学载体往往蕴含着丰富的数学思想和深刻的教育内涵.笔者对这部分内容作了一些研究,在研究和教学实践过程中一直思索如下三个问题:一是哪种方法更贴近学生实际?二是怎样揭示数学本质的思维,培养学生能力?三是怎样让学生快速、有效记忆数学知识和结论,以达到切实理解和准确运用?

2.2 问题的解决

方法：左右侧判定法.

背景:在平面直角坐标系中,一旦直线Ax+By+C=0(A2+B2≠0)的位置确定,则直线把平面区域分为“左上、右下”和“左下、右上”两大类情况,如图1、图2.

图1

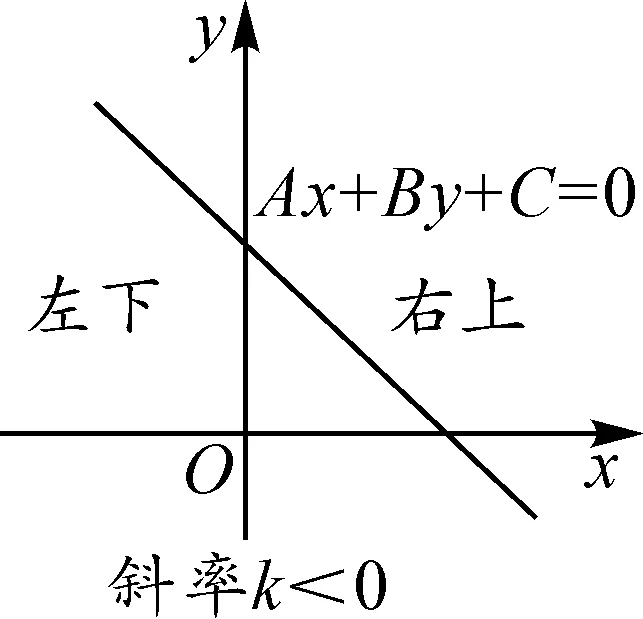
图2

结论1对于二元一次不等式Ax+By+C>0或Ax+By+C<0(A2+B2≠0),若A>0,则有:

不等式Ax+By+C<0表示的区域,在直线Ax+By+C=0的“左侧”(含左上、左下);

不等式Ax+By+C>0表示的区域,在直线Ax+By+C=0的“右侧”(含右上、右下).

背诵口诀:(在A>0的前提下)不等号小于零,区域在直线左侧;不等号大于零,区域在直线右侧.简称“左小右大”!

证明及思维引导(以斜率为正的情况为例):

设f(x,y)=Ax+By+C(A2+B2≠0).

(1)在直线左侧任取一点P1(x1,y1),则它离直线“有一小段距离”,想一想怎样才能“刻画或计算”这个距离?

(2)引导学生作直线y=y1交直线l于点P0,设P0的坐标为(x0,y1),如图3,则“距离”可以考虑用与“x1-x0”相关的式子来表示.

图3

(3)进一步思考,怎样计算能够出现“x1-x0”?

(4)由P0(x0,y1)在直线l上,则f(x0,y1)=0.

考虑f(x1,y1)=f(x1,y1)-f(x0,y1)=(Ax1+By1+C)—(Ax0+By1+C)=A(x1-x0).

因为P1(x1,y1)在直线l左侧,所以x1-x0<0,而A>0,则f(x1,y1)-f(x0,y1)<0,故f(x1,y1)<0,即直线左侧区域的点(x,y)必满足Ax+By+C<0.

因此A>0时,不等式Ax+By+C<0表示的区域在直线Ax+By+C=0的“左侧”.

同理,若在直线右侧取点,则x1-x0>0,由A>0,得f(x1,y1)-f(x0,y1)>0,故f(x1,y1)>0,即直线右侧区域的点(x,y)必满足Ax+By+C>0.

因此当A>0时,不等式Ax+By+C>0表示的区域在直线Ax+By+C=0的“右侧”.

2.3 结论的推广

根据结论1不难得出直线l同侧的两个点对应的二元函数的值符号相同,异侧的两个点对应的二元函数值符号相反,于是有如下结论:

结论2已知二元一次函数f(x,y)=Ax+By+C(A2+B2≠0),则有:

①点P1(x1,y1),P2(x2,y2)在直线Ax+By+C=0同侧⟺f(x1,y1)·f(x2,y2)>0;

②点P1(x1,y1),P2(x2,y2)在直线Ax+By+C=0异侧⟺f(x1,y1)·f(x2,y2)<0.

证明略,可以留作学生思考.相信在结论1的基础上,结论2很容易被学生接受.

3 方法对比和体会

“取点判别法”,即取特殊点,计算函数值,判断点与直线的位置关系再确定平面区域.而“A,B符号判别法”需由A(或B)的符号与不等式的符号的异同来确定平面区域,其口诀“同上异下”“同右异左”的理解具有一定的难度.

相比之下,笔者认为“左右侧判定法”是对“A符号判定法”的深化和进一步简便,优势在于:

(1)从根本上避免了“取点判别法”和“A,B符号判别法”中代入求f(x1,y1)的计算过程;

(2)先将不等式(或直线)的系数A化为“正”,符合直线的“一般式方程”系数A为正的要求,以及学生的一般思维习惯;

(3)对于给定的二元一次不等式(组),要快速判定相关区域得到线性规划问题的“可行域”只需两步:①在坐标系中快速画出直线Ax+By+C=0(A2+B2≠0).②依据结论1的口诀“左小右大”,快速确定相关区域.

4 运用举例

解：在坐标系中分别作出两条直线(如图4),则x-3y+6<0表示的平面区域在直线x-3y+6=0(虚线)左上侧,x-y+2≥0表示的区域在直线x-y+2=0(实线)的右下侧,故可行域应是图中的阴影区域,且两直线的交点坐标为(0,2).

图4

设z=2x+y,得y=-2x+z,当斜率为-2的直线经过点(0,2)时,纵截距z最小,且zmin=2×0+2=2.

故2x+y的取值范围是(2,+∞).