解题中化归转化的“五种策略”

江苏省苏州市吴江中学 贺姣妮

数学解题的实质是数学知识与数学思维的化归与转化过程.因而在实际解题过程中,要从题设条件入手,朝着结论的方向,从不同视角、不同侧面、不同知识等方面去探讨问题的破解,寻求合理有效的解题途径与方法.在此过程中,要遵循化归与转化过程中的熟悉化原则、简单化原则、直观化原则等一些基本原则.本文中结合实例,就解题过程中化归转化的基本解题策略加以剖析.

1 正向向逆向的转化

问题的题设和结论之间往往存在着一定的因果关系和辩证关系.具体解题时,若从问题的正面入手切入时思维受阻,可以反其道,从它的反面出发,借助逆向思维,经常可以收获不错的效果,另辟捷径.

例1(2022年高考数学新高考Ⅱ卷·5)甲、乙、丙、丁、戊5名同学站成一排参加文艺汇演,若甲不站在两端,丙和丁相邻,则不同的排列方式共有( ).

A.12种 B.24种 C.36种 D.48种

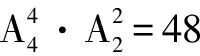
所以甲不站在两端,丙和丁相邻的不同排列方式有48-24=24种.

故选择答案:B.

点评：从正面入手,情况比较复杂,不易操作;合理转化,从反面视角切入,确定“甲站在两端”的不同排列方式,进而利用补集思维进行分析,处理起来更加直接有效.在破解一些涉及“不”“至少或至多”等相关问题时,经常借助补集思维,通过正向向逆向转化来分析与处理.

2 局部向整体的转化

问题往往由局部与整体进行合理有效的组合而形成,在解决一些比较复杂的数学问题时,可以从总体角度加以把握,从整体入手,秉持全局观念,不单打独斗,往往会有不错的收获.

例2(2021年云南省玉溪市峨山一中高考数学三模试卷)为了给数学家帕西奥利的《神圣的比例》画插图,列奥纳多·达·芬奇绘制了一些多面体,如图1的多面体就是其中之一.它是由一个正方体沿着各棱的中点截去八个三棱锥后剩下的部分,这个多面体的各棱长均为2,则该多面体外接球的体积为( ).

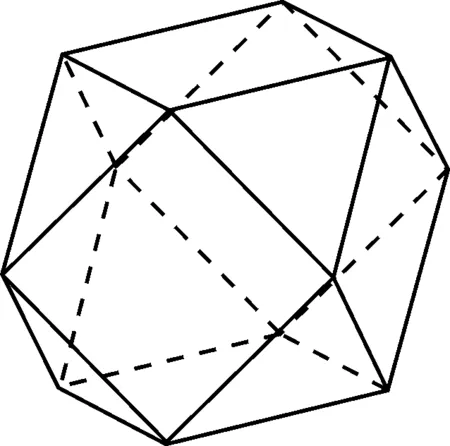
图1

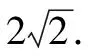
图2

此时正方体的中心即为多面体外接球的球心.

故选择答案:D.

点评：从条件入手直接利用多面体外接球的性质来处理,不易找到突破口,容易出错;而把多面体还原补形为正方体,进而确定正方体的中心即为多面体的外接球的球心,从局部还原到整体,合理化归与转化.从局部上升到整体,从另一个视角来分析,往往会有不错的效果.

3 未知向已知的转化

类比化归与转化是知识迁移与学习能力提升的一种基本途径.数学解题中,往往要抓住题目中已知关键信息,将未知的结论与已知的条件进行类比转化与类比推理,答案往往就在其中,巧中取胜.

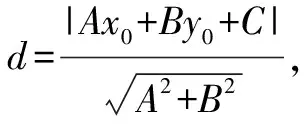
点评：从平面中点到直线的距离公式这一已知信息入手,通过合理化归与转化,利用类比推理可得空间中点到平面的距离公式,化未知为已知,实现问题的转化与突破.类比推理往往可以实现低维度向高维度的化归与转化,实现未知向已知的过渡与转变,突破界限.

4 抽象向具体的转化

对于一些抽象的数学问题,可以结合抽象问题的几何意义或其他特征,合理具体化,构建联系,建立与之对应的数学模型,将其转化为熟知的数学问题,从而启迪解题思路,寻找解决问题的突破口[1].

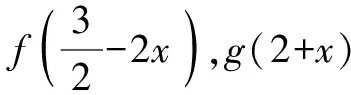
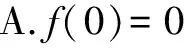
C.f(-1)=f(4) D.g(-1)=g(2)

分析：依题意,通过特值法,探寻特殊的函数,结合原函数与导函数所对应的函数均是偶函数,引入三角函数加以合理构造.

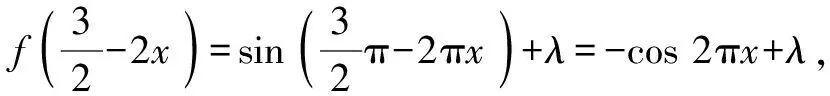
而g(x)=f′(x)=πcos πx,则有g(2+x)=πcos(2π+πx)=πcos πx,故g(2+x)也是偶函数.

因此,以上构造的特殊函数f(x)满足题目条件.

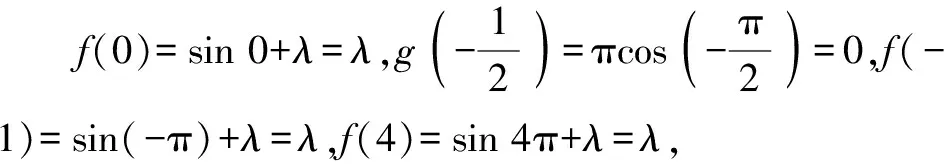
综上分析,选项BC正确.故选择答案:BC.

点评：由抽象函数的基本性质,构建与之相应的具体的特殊函数,实现抽象向具体的转化,进而利用特殊函数进行求值与判断.构建满足题设条件的数学模型,是实现抽象向具体转化的一种基本手段,也是破解数学小题比较常用的一种特殊技巧方法.

5 个别向一般的转化

华罗庚说过:“善于退,足够地退,退到最原始而不失去重要性的地方,是学好数学的决窍.”具体解题时,可以借助特殊现象的研究,再借助类比、分析、归纳、迁移等去概括一般性的规律,由此实现问题的解决.

A.-3 B.-2 C.0 D.1

解析：令x=1,y=0,则有f(1)+f(1)=f(1)·f(0),结合f(1)=1,可得f(0)=2.

令y=1,可得f(x+1)+f(x-1)=f(x)f(1)=f(x),即f(x+1)=f(x)-f(x-1),所以

f(2)=f(1)-f(0)=-1,f(3)=f(2)-f(1)=-2,

f(4)=f(3)-f(2)=-1,f(5)=f(4)-f(3)=1,

f(6)=f(5)-f(4)=2,f(7)=f(6)-f(5)=1,归纳可知f(x)的周期为6.

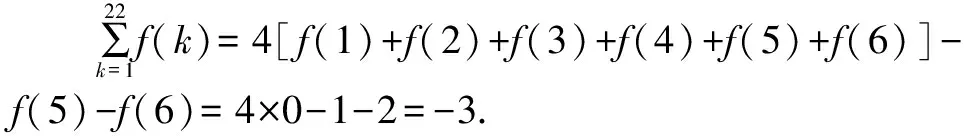
故选择答案:A.

点评：根据题设抽象函数所满足的关系式,借助特殊赋值法处理,构建相应的函数递推关系式,利用前若干项函数值的求解,由个别到一般加以转化,通过归纳来确定函数的周期性,进而利用函数的周期性来分析与求解.归纳推理往往可以达到从个别到一般的转化与应用,也是破解问题常用的一种推理方式.

著名的数学家、莫斯科大学教授C.A.雅洁卡娅曾在一次向数学奥林匹克参赛者发表《什么叫解题》的演讲时提出:“解题就是把要解题转化为已经解过的题.”在实际的数学解题过程中,其实质就是从未知向已知、从复杂到简单、从抽象到具体等的转化.合理熟练掌握一些基本的解题转化策略,可以开拓数学思维,优化数学品质,提升数学能力,培养数学核心素养[2].