抛物线中“切点三角形”性质的探究及应用

安徽省铜陵市义安区教育体育局教研室 陶 俊

1 抛物线“切点三角形”及其性质

过抛物线外一点P(x0,y0)作抛物线y=ax2+bx+c的两条切线PA,PB,A,B为切点(如图1),M为AB的中点,连PM交抛物线于点N,称△PAB为“切点三角形”,它具有如下性质:

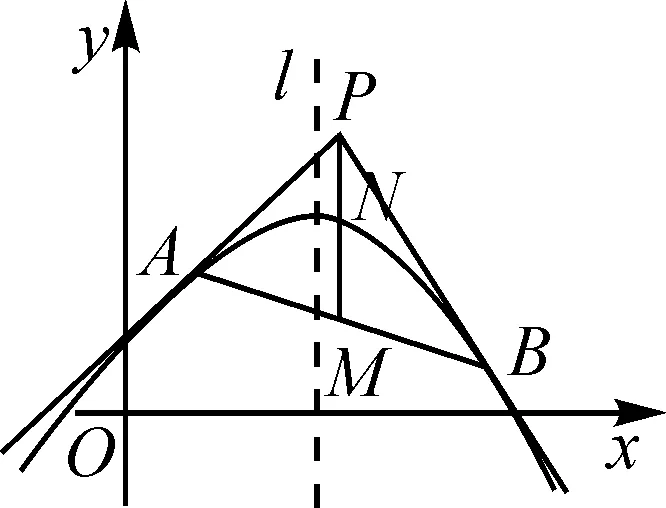
图1

性质1“切点三角形”的一条中线平行抛物线的对称轴l,即PM∥l.

性质2“切点三角形”的一条中线被抛物线平分,即PN=MN.

这里f(x0)是当x=x0时抛物线y=ax2+bx+c(a≠0)的值f(x0)=ax02+bx0+c.

图2

2 抛物线“切点三角形”性质的证明

设其切线方程为y-y0=k(x-x0),与抛物线方程联立,整理得到

ax2+(b-k)x+c+kxo-y0=0.

由PA,PB与抛物线y=ax2+bx+c相切,得Δ=0,即(b-k)2-4a(kx0-y0+c)=0,亦即k2-(2b+4ax0)k+b2+4ay0-4ac=0,则

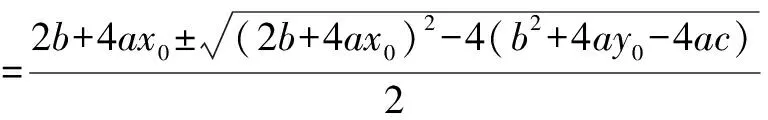
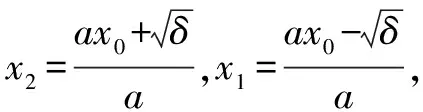
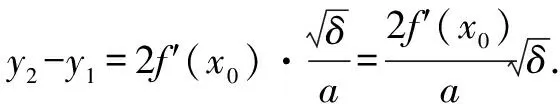
整理,得y+y0=2ax0x+bx+bx0+2c=f′(x0)x+bx0+2c.

所以直线AB的方程为y=f′(x0)x+bx0-y0+2c.

又点A,B在抛物线上,联立方程消去y,得

ax2+bx+c=f′(x0)x+bx0+2c-y0.

故AB的中点坐标为M(x0,2f(x0)-y0),又P的坐标为(x0,y0),则PM∥l.性质1得证.

这里,PN2=(f(x0)-y0)2,

所以,有

①

由平面几何可知,在△PAB中,PM是AB边上的中线,根据三角形中线定理,可得

②

由①②式,可得4PN2=PM2,即2|PN|=|PM|.所以N是PM的中点,PN=MN.性质2得证.

3 抛物线“切点三角形”性质的应用

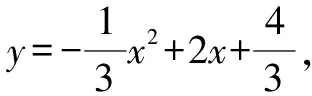
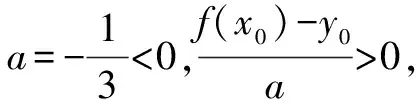
所以△PAB的面积为18.

例2如图3,从抛物线上A(1,3),B(3,-1)两点分别作抛物线的切线交于点P,若△ABP的面积为10,求抛物线的解析式.

图3

解析：取AB中点M并连接PM交抛物线于点N,由切点三角形性质1,可知PM平行于y轴,N为PM的中点.由A(1,3),B(3,-1),得M(2,1).

所以P(2,-9),N(2,-4).

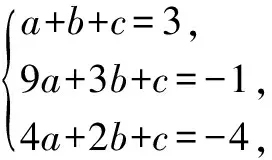
因此抛物线的解析式为y=5x2-22x+20.

对于例1用常规方法,可以先计算两切点A,B的坐标,再利用三点坐标求三角形PAB的面积.这显然大费周折,用上面的方法要简便很多.对于例2也许用普通的方法就不好应对了,而用抛物线切点三角形的性质1则可迎刃而解,似乎“山重水复疑无路,柳暗花明又一村”.