锂离子电池均衡控制策略

2023-11-09刘自南吴铁洲

实验室研究与探索 2023年8期

刘自南，王斌，吴铁洲

（1.重庆科技学院电气工程学院，重庆 401331；2.重庆机场集团有限公司扩建指挥部，重庆 401120；3.湖北工业大学太阳能高效利用及储能运行控制湖北省重点实验室，武汉 430068）

0 引言

锂离子电池被广泛应用于电动汽车，无人机，风力/光伏发电等储能系统［1］。通常情况下，一节锂离子电池的电压以及容量有限，很难满足实际应用场景的需求，所以更多情况下需要将多节锂离子电池串联以及并联来满足负载需求。然而，锂离子电池串并联使用多次后，由于制造以及使用环境存在差异，使得电池出现较大的不一致，而这种不一致会增加电池出现安全隐患的概率，并且会极大缩短电池使用寿命，电池均衡是目前常用的解决方案［2］。

在电池均衡中，通常会根据电池两端的电压，判断电池是否需要均衡［3］。这是因为电池两端的电压非常容易获得，并且它与电池荷电状态（State of Charge，SOC）存在一定关系［4］。虽然有部分文献提出以电池SOC为指标比电压更合适［5］，但是估算电池组间所有电池的SOC是不切实际的，电池端电压并不能完全反应电池SOC，这是因为电池端电压不仅仅与SOC 有关，还与电池温度，电池充放电电流等因素有关［6］。同时，电池间电压之差通常很小，而上述因素对电池电压的影响，相较于电池之间电压之差不可忽略，这就导致目前的均衡控制策略可能无法对电池进行较好地均衡。

针对上述问题，有很多学者对此做了大量研究，梁光胜等［7］通过电流等参数，估算出电池开路电压（Open Circuit Voltage，OCV），以电池间OCV 之差为指标进行均衡，Wang 等［8］通过增加额外的指标对电池间电压之差进行修正，Kim 等［9］则是提出一种新的策略，通过将电池间电压之差转换为SOC 之差进行均衡。上述文献都有一定的正面效果，但是在实施方面却非常复杂，并不适合实际使用。

本文通过分析电池均衡末期端电压变化与均衡电流的关系，基于电池直流内阻，在电池均衡末期增加额外的均衡电流压降补偿，以获取比目前通用的均衡策略更优的均衡效果。

1 均衡策略原理

1.1 电池二阶模型

为了解电池均衡策略原理，需要建立等效电路模型。二阶等效电路模型已被证实能够较好地兼顾精度以及计算量，且被广泛应用［10］，故本文也使用二阶模型进行分析。

图1 所示为二阶等效电路，由图可知，UOCV是电池的OCV电压，R0是电池的欧姆内阻，R1、R2、C1和C2分别是电池的极化电阻和极化电容，而U则是电池的端电压，I为电池充放电电流。根据文献［11］中的推导，UOCV可表示为

图1 二阶等效电路

式中：UP1（0）和UP2（0）分别为R1/C1以及R2/C2上0时刻的极化电压；t为时刻；τ1和τ2为时间常数，即

1.2 均衡电流压降补偿

一般来说，当传感器测得两节电池端电压之差大于某一阈值时，电池管理系统（Battery Management System，BMS）会启动均衡，而当这两节电池电压之差相等时，BMS 会关闭均衡［12］，假设电池组中电池A 的SOC最高，电池B的SOC最低，当满足

BMS会关闭均衡。

电池在成组之前都会经过严格的老化筛选流程，所以可以认为电池在出厂前参数是一致的［13］。而电池均衡的本质是通过改变电池的充放电电流大小进而让SOC 高的单体电池放电更快或充电更慢，实现与SOC低的单体电池SOC 一致的目的。若电池A 和B均在放电，而BMS通过均衡电路为电池B提供额外的充电均衡电流，若满足

BMS会关闭均衡。式中，Ibal为均衡电流。通常情况下，对于除磷酸铁锂电池的其他锂离子电池，其时间常数一般在1 min 内［14］，假设电池τ1和τ2均为1 min，则4 min后，电池由于极化电容所导致的极化电压只有初始状态的0.018 倍。通常情况下，电池均衡并不是一个很快的过程，一般需要十几分钟甚至数小时才能实现电池均衡的目标［15］，所以，在电池均衡末期，可以认为均衡电流给电池带来的影响已进入稳态，电池A与B的压差可由下式表示：

式中：UA、UB分别为电池A、B 的端电压。Rd为电池直流电阻，其值为R0及R1和R2之和，Rd是电池在成组之前会筛选的量［16］，可以默认是已知的。

1.3 控制流程图

所提出的均衡策略控制流程如图2 所示。图中，Us为设定的均衡开启阈值。由图可知，提出的均衡控制策略非常简单，与通用均衡策略相比，提出均衡控制策略额外需要的量为Ibal以及Rd，而Ibal是BMS在运行过程中需要采集的重要参数，Rd则是在电池出厂前就会获得的参数，所以相较于目前常用的均衡控制策略，所提出的均衡控制策略基本上没有任何工作量，非常易于实施。

图2 均衡策略控制流程

2 均衡电路

为验证所提出控制策略的优越性，图3 所示为进行验证使用的均衡电路。由图可知，所用的均衡电路非常简单，对于电池组，有2 个开关控制均衡电源正负极以及电池正负极相连，进而控制均衡。同时电流传感器会采集均衡电流大小，实时提供数据供BMS分析判断。

本文使用7 串5 并共35 节三元锂离子组成的电池组进行实验测试，电池组标称电压为26.6 V，容量为10 Ah。主控芯片采用MC9S12XET256，电压采集芯片使用LTC6803。当电池组中有单体电池电压过低，需要被均衡时，由充电机为需要被均衡的电池提供5 V/2 A的电源充电，为进行充电，在均衡通道中，使用ACS712-05 芯片采集电池的均衡电流。所有的数据通过控制器局域网（Controller Area Network CAN）发送到上位机，均衡开启以及结束过程，当连续多次判断出BMS应该均衡或停止均衡时，BMS 才会动作，否则维持状态不变，BMS硬件电路如图4 所示。

图4 BMS硬件电路

实验通过上位机接收并保存BMS上报的数据，上位机界面如图5 所示。

图5 上位机界面

3 实验结果与分析

3.1 放电状态下实验结果与分析

（1）7 节电池通用均衡策略。一般电池组处于放电状态时，检测电池间端电压一致时停止均衡，电池组中7 节电池的电压变化如图6 所示。

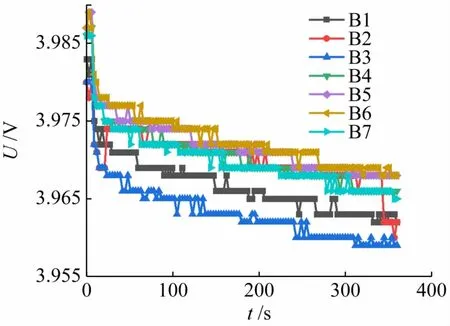
图6 电池组中7节电池的电压变化

（2）2 节电池通用均衡策略。为方便分析，只展示前所述的电池A与B的电压变化情况，应用通用均衡策略电池组放电时，电池A与B 的电压变化如图7所示。当电池刚刚处于放电状态时，电池电压出现了较大幅度的下降，这是电池欧姆压降以及极化压降所导致的。在10 s 左右，开启恒流源开关，恒流源将为电池B进行充电均衡，此时电池B 的电压有明显上升，但是在此瞬间，电池的SOC并没有变化，印证了之前的分析，在电池结束均衡前，需要将均衡电流带来的电压误差进行消除。之后，电池电压在缓慢下降，到约第340 s，BMS结束均衡，此时电池B与A的端电压一致，但停止均衡后，电池B 的电压出现较大的回落，导致与电池A的电压之间具有较大的差异，最终二者电压之差约为7 mV。

图7 通用均衡策略下电池组放电时电池A与B电压变化

（3）本文均衡策略。应用本文均衡策略电池组放电时，电池A与B的电压变化如图8 所示。在放电期间电池A和B的电压变化情况与图7 相似，只不过在约第180 s，即使电池A和B的电压几乎相等，但BMS并没有停止均衡，由于所提出的策略增加了额外的均衡电流补偿，这就使得电池B在与电池A电压相等的基础上，还要额外增加均衡电流补偿的电压值，才会认为电池B被较好地均衡。到约第460 s，BMS停止均衡，此时电池B的电压要比电池A 的电压高，但是当均衡停止后，电池B 的电压出现回落，使得其电压低于电池A的电压，最终二者压差约2 mV。

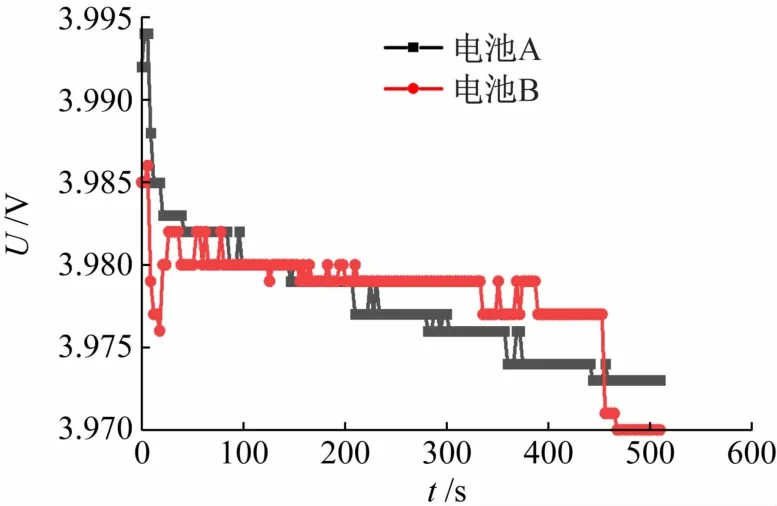
图8 本文均衡策略下电池组放电时电池A与B的电压变化

3.2 静置状态下实验结果与分析

（1）通用均衡策略。应用通用策略电池组静置时，电池A与B的电压变化如图9 所示。在约第10 s，开启恒流源后，电池B 的电压存在较大幅度的上升，之后由于恒流源的存在，电池B 的电压在缓慢上升，直至约第80 s，BMS才停止均衡。在约第60 s，电池B与A的电压一致，但此处并没有连续多次达到均衡关闭条件，故被芯片滤掉，BMS 并没有动作。BMS 停止均衡后，电池B 的电压出现较大回落，最终与电池A的电压差约为9 mV。

（2）本文均衡策略。应用本文策略电池组静置时，电池A与B的电压变化如图10 所示。在约第380 s，电池B的电压远高于电池A的电压时，BMS 才结束均衡，而在约第50 s至约第380 s，即使电池B的电压高于电池A的电压，造成“过均衡”的假象，BMS 却并没有动作。当BMS停止均衡后，电池B的电压出现较大回落，最终趋于稳定，电池B和A的最终压差约为2 mV。

图10 本文均衡策略下电池组静置时电池A与B的电压变化

3.3 本文所提出策略性能分析

当均衡目标都是实现电池电压一致时，使用通用的电压均衡控制策略，其最终误差分别为7 与9 mV，而本文的补偿策略均为2 mV，其在性能上要优于常用的均衡控制策略。在实施上，根据前面的分析，所提出的均衡控制策略只需要均衡电流以及直流电阻2 个量，而均衡电流是可以通过传感器直接获取的，直流电阻则是可以通过电池在出厂前筛选配组获得的，所以这2 个量在获取过程中没有任何难度，也就是说，所提出的策略跟目前通用的策略一样简单，但是却可以获得更优的性能表现。