磷酸铁锂并联电池组充电安全性界定

王丽梅，盘朝奉，刘 良

(江苏大学汽车工程研究院，江苏镇江212013)

磷酸铁锂电池因其长寿命和高稳定性，在储能系统及电动汽车领域被广泛关注，但成组后动力电池组寿命及安全问题却制约其进一步应用和发展[1]。电池截止电压及容量作为电池安全充放电控制的基本参数，是避免电池过充/放，确保电池安全、提高电池使用寿命的基础[2]。

为了达到较高的可用容量，动力电池组一般是将多个单体电池并联成单节电池[3]。若单体电池间不存在差异，单节电池容量可通过单体电池容量与并联单体电池数乘积得到。不一致的使用环境会导致单体电池间老化速率的差异[4]。单节电池容量需重新定义为充电截止电压到放电截止电压间总放出容量。单体电池间老化差异表现为容量及内阻的差异，此差异会导致流经单节电池内各单体电池电流不一致，即单体电池充放电速率存在差异，影响单节电池充电截止电压，进而影响单节电池容量。本文基于单体电池使用安全性，围绕单体电池老化对单节电池充电截止电压的影响进行研究。

1 电池模型建立及验证

采用实验的方法，很难得到具有特定老化状态的单体电池，因此研究工作借助仿真技术进行。在众多仿真模型中，一阶、二阶RC等效电路模型计算简单、参数提取方便，因而比较适合描述锂电池电化学行为[5]，文献[6]指出一阶RC等效电路模型即可恰当地描述电池使用过程中的动态特性。

一阶RC等效电路模型原理如图1所示。图中：Voc为电池开路电压；R0为电池欧姆内阻；R1及C1分别为电池极化内阻与电容；I为流过电池的总电流；V为电池端电压。文献[7]指出Voc、R0、R1、C1与电池荷电状态(state ofcharge,SOC)及温度有关。

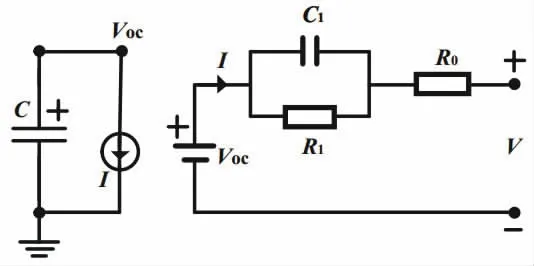
图1 一阶RC等效电路模型原理

一阶 RC 等效电路模型中模型参数Voc、R0、R1、C1常基于查表方式实现，表格的输入参数为电池温度及SOC，输出参数为电池模型参数。电池温度计算基于能量守恒定律，SOC估算采用安时积分法。依据上述原理，利用Simscape语言建立图2所示单体电池仿真模型，并基于该仿真模型构建了不同拓扑结构的串、并联电池组模型，具体模型建立及验证参见文献[6]，仿真与实测结果最大误差不超过1%，表明基于Simscape平台建立的单体电池模型可用于不同拓扑结构电池组模型构建。

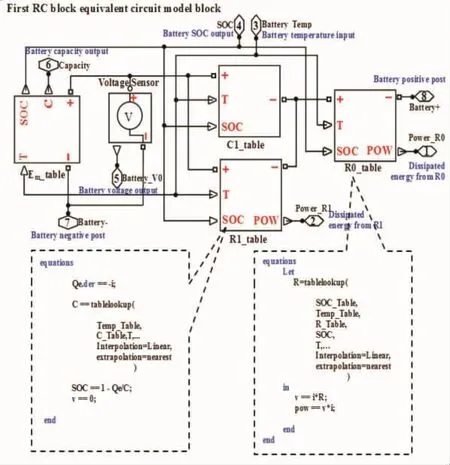
图2 单体电池仿真模型

2 单体电池老化对单节电池性能的影响

图3显示了常温下实测的JL-8Ah磷酸铁锂单体电池容量和欧姆内阻随电池循环次数变化的情况。由图3可见，随着循环次数的增加，电池容量及欧姆内阻呈近似线性的变化规律，这与文献[8]的结论类似。每循环100次，电池内阻增加约3.86%，容量衰减约1.18%。

图3 单体电池容量及内阻随循环次数的变化曲线

因电池放电过程受制于运行工况，电流变化剧烈，间隙性的放电电流导致并联单体电池间存在自均衡现象；而充电过程中电流一般恒定，因此本文选择充电过程中单体电池老化对电池组性能的影响进行讨论。

为描述方便，定义拓扑结构“p-s”表示p节单体电池并联构成单节电池，s串单节电池串联构成电池组。文献[9]指出，当电池容量降至初始容量的80%时，电池不宜再作动力电池使用。拓扑结构为“20-2”的7.2 V、160 Ah电池组模型，假设某一单体电池因老化容量降为初始容量的80%，分析该单体电池对充电过程中单节电池性能的影响。为了便于描述，定义这一容量衰减的单体电池为“老化单体电池”，包含“老化单体电池”的单节电池为“老化单节电池”，内部单体电池容量均未出现衰减的单节电池为“正常单节电池”。

参考充电电流0.3C～1C的建议[10]，选择了1C(160 A)仿真充电电流，初始状态单节电池SOC为0，结束条件为某一单体电池SOC为0.995(假设此时单节电池充满电)，图4显示了相应的仿真结果。由图4(a)所示的不同单节电池的端电压变化曲线可知，“老化单节电池”与“正常单节电池”的端电压差值在电压平台期基本稳定，充电末期则有较大差异。单节电池端电压主要受制于电池开路电压、欧姆内阻、极化内阻及电流，“老化单节电池”在充电末期欧姆内阻与极化内阻增加，从而出现了其端电压与“正常单节电池”端电压差值大幅增加的现象，故可利用充电过程末期单节电池端电压差异识别“老化单节电池”。

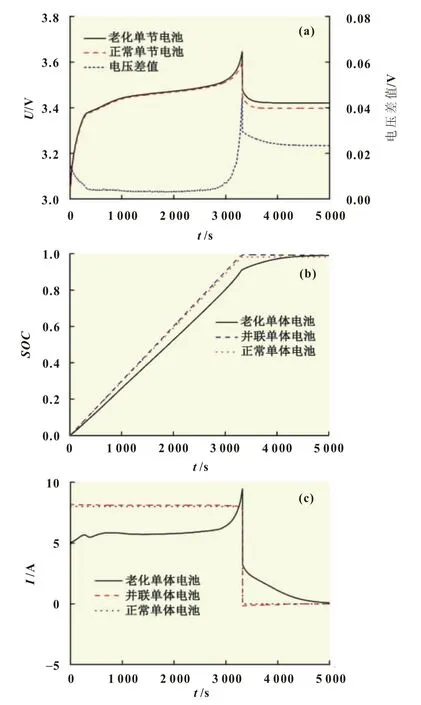
图4 某一单体电池容量为初始容量80%的仿真结果

图4(b)显示了充电过程中不同单体电池SOC的变化曲线。“正常单节电池”内各单体电池参数接近，其特征参数可表征其内部各“正常单体电池”特征参数。随着充电过程进行，与“老化单体电池”并联的“并联单体电池”较“正常单体电池”率先进入过充电状态，而“老化单体电池”SOC上升速率较其他单体电池低。充电结束时，“并联单体电池”SOC为0.995，“老化单体电池”SOC为0.910，此时“正常单体电池”SOC为0.981。参照图4(c)可看出“并联单体电池”因流经其电流较大，SOC上升速度增加，最先进入过充电状态；与“正常单体电池”相比，“老化单体电池”SOC上升速度较慢，这是因为相对于电池容量降低，单体电池内阻增加对SOC的影响占主导地位。

从图4(b)还可以看出，充电过程中“老化单节电池”内各单体电池SOC间最大偏差达0.085，故利用“老化单节电池”SOC表征其内部各单体电池SOC并不合适。本文仅针对拓扑结构为“20-2”的电池组假设某一单体电池处于老化状态的情况展开分析，若单节电池内并联单体电池数降低或老化单体电池数增加，“老化单节电池”内各单体电池SOC间偏差将进一步增大。实际使用过程中，无法对流经并联单节电池内部所有单体电池的电流进行监测，故为保证单体电池安全，需根据电池老化状态重新调整单节电池充电截止电压。

3 单节电池安全充电截止电压讨论

实际应用过程中，单节电池老化状态难以确定。为保证电池组中各单体电池使用安全，需对不同老化状态下的单节电池充电截止电压变化规律进行分析，以确定包容“老化单节电池”的安全充电截止电压限值。

同样是拓扑结构为“20-2”的7.2 V、160 Ah电池组模型，仿真充电电流为1C，初始状态为单节电池SOC为0，结束条件是某一单体电池SOC为0.995。设定电池组中“老化单体电池”容量均为初始容量的80%。图5对比了“老化单节电池”中包含不同“老化单体电池”数目，充电结束时“老化单节电池”及“正常单节电池”的电压值。由图5可见，充电结束时，“老化单节电池”端电压随“老化单体电池”数目的增加而降低。全寿命周期范围内“老化单节电池”最低充电截止电压为3.60 V，此时单节电池SOC为0.982。考虑到实际使用过程中难以判断每节单体电池的具体老化状态，可将整个循环寿命过程中出现的最低充电截止电压界定为单节电池安全充电截止电压。

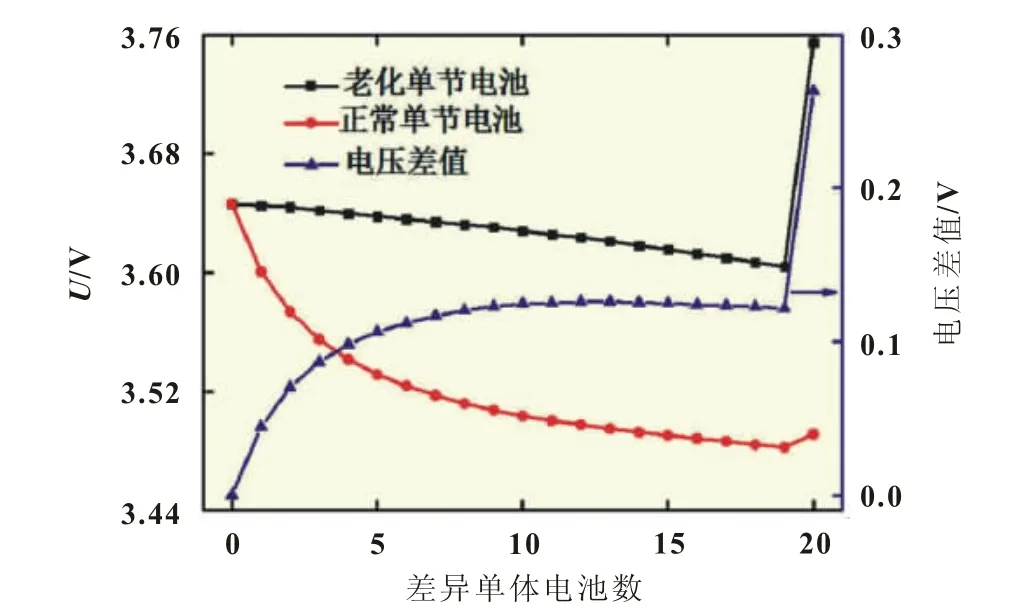
图5 不同差异单体电池数的仿真结果

由图4(b)可知，充电过程中，与“老化单体电池”并联的“正常单体电池”SOC率先达到0.995，当“老化单体电池”整体内阻最大时，流经“并联单体电池”的电流最大，此时安全充电截止电压最低。“老化单体电池”整体内阻呈最大值的条件为各差异单体电池具有相同的老化状态，即老化后的容量与内阻相同。

从图5中可以看出，“老化单节电池”最低充电截止电压出现在老化单体电池数为19，即“老化单节电池”内仅包含一只“正常单体电池”的情况下。仍取单节电池容量为初始容量的80%左右作为动力电池应用限值，包含n节单体电池的单节电池的安全充电截止电压将出现在其包含n－1节“老化单体电池”，各“老化单体电池”容量均降为初始容量的极限状态下。以这种极限状态为约束，对不同充电电流及并联单体电池数下的单节电池安全充电截止电压进行了仿真，图6显示了相应的仿真结果。

从图6可以看出，随着充电电流增大，仿真得到的安全充电截止电压呈先降低后上升趋势。流经并联单体电池间的电流差异随充电电流的降低而降低，使得充入单节电池的容量增大，最终带来安全充电截止电压的增大。参考图4(c)可知，充电电流的增大易导致“并联单体电池”过早进入充电末端，而此时“老化单体电池”仍处于充电平台期。充电末端“并联单体电池”内阻将进一步增大，此时流经两电池的电流差异将缩小，进而出现安全充电截止电压随充电电流增大而增加的现象。故实际使用过程中，安全充电截止电压随电流变化的影响可以忽视，仅考虑单节电池结构，以极限状态下的单节电池充电截止电压界定安全充电截止电压。

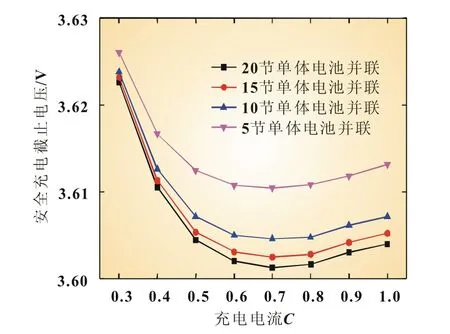
图6 不同充电电流和并联单体电池数下的单节电池安全充电截止电压

4 结论

本文基于Matlab/Simscape平台开发了电池仿真模型，利用此模型仿真分析单体电池老化对充电过程中并联电池组性能的影响，结果表明：

(1)与“老化单体电池”并联的单体电池因充电电流较大，其SOC上升速率高于其余单体电池，为了保证并联单体电池安全，需依据单节电池老化状态重新调整电池充电截止电压。

(2)包含n节单体电池的单节电池最低充电截止电压出现在单节电池内部只有一节正常单体电池，其余单体电池容量均降为初始容量的极限状态下。

(3)实际使用过程中，可以忽视充电电流对安全充电截止电压的影响，仅考虑并联单体电池数，以极限状态下的单节电池充电截止电压界定安全充电截止电压。

[1]张维戈,时玮,张言茹,等.大容量锂离子电池的并联性能评估与等价性分析[J].电网技术,2014,38(6):1499-1504.

[2]郑岳久.车用锂离子动力电池组的一致性研究[D].北京:清华大学,2014.

[3]MAO S W,CHANG Y L.Numerical simulation for the discharge behaviors of batteries in series and/or parallel-connected battery pack[J].Electrochimica Acta,2006,52:1349-1357.

[4]KENNEY B,DARCOVICH K.Modelling the impact of variations in electrode manufacturing on lithium-ion battery modules[J].Journal of Power Sources,2012,213:391-401.

[5]TARUN H.High fidelity electrical model with thermal dependence for characterization and simulation of high power lithium battery cells[C]//Proceedings of 2012 IEEE Electric Vehicle Conference(IEVC).Greenville,South Carolina,USA:IEVC,2012:1-8.

[6]WANG L M,ZHAO X L,LIU L,et al.Battery pack topology structure on state-of-charge estimation accuracy in electric vehicles[J].Electrochimica Acta,2016,219:711-720.

[7]MASSIMO C,GIOVANNI L,TARUN H.Experimentally determined models for high-power lithium batteries[C]//SAE Paper.Detroit,Michigan,USA:Advanced Battery Technology,2011:2011-01-1365.

[8]李哲.纯电动汽车磷酸铁锂电池性能研究[D].北京:清华大学,2011.

[9]HUBBMAN J.Battery Reference Book[M].Missouri,USA:Bitrode Corporation,2001.

[10]文锋,姜久春,张维戈,等.电动汽车用锂离子电池组充电方法[J].汽车工程,2008,30(9):792-795.