基于群智能算法优化LSTM的催化裂化预测研究

2023-11-09洪娟田文德

山东化工 2023年18期

洪娟,田文德

(青岛科技大学化工学院,山东青岛 266042)

在中国,催化裂化装置生产的柴油和汽油分别占成品油的30%和70%[1]。催化裂化装置是炼油厂汽油和柴油的核心生产装置,是炼油厂的重要创收来源[2]。催化裂化过程的数字化和智能化在DCS的辅助下得到了大力发展[3]。利用大数据处理技术对积累得到的大量催化裂化操作数据进行数据挖掘分析,对其进行主要控制变量预测,可以提升催化裂化装置运行的平稳安全性。近年来,基于深度网络实现对过程参数的有效预测效果研究得到了广泛关注[4]。LSTM是一种能够有效地提取得到时间序列数据间依赖关系的神经网络[5]。

Zhao等人[6]通过使用不一样时间尺度的数据分别训练神经网络,获得不一样时间尺度的时间序列特征,并将其应用于时间序列预测,此方法有效提高了预测精度。Liu[7]曾提出基于主成分分析和反向传播神经网络(BP)的预测模型。通过主成分分析去除了影响因素之间的线性相关性,并将主成分分析得到结果当作BP神经网络的输入。Tao等人[8]提出使用TreNet模型来预测多模态融合的未来趋势,通过CNN学习得到当前时间序列特征,通过LSTM学习得到时间序列的趋势特征,这个研究方法拥有更强的特征提取学习能力。

长短期记忆神经网络预测模型包含着许多网络参数,如核函数、学习率和神经元数量等,这些参数都会影响LSTM模型的预测精度,因这些参数过分依赖于经验设置致使其预测精度不稳定。与此同时,随着参数设置的不同,LSTM模型的训练时间长度也会发生变化。利用粒子群算法对LSTM模型的部分网络参数进行搜索,可以解决人工选择参数的问题。针对人工参数设置导致模型的精度低、泛化能力弱等问题,采用搜索范围广、收敛速度快的粒子群算法(PSO)和布谷鸟算法(CS)对LSTM的一些超参数进行优化,构建PSO-LSTM模型和CS-LSTM模型,寻找到LSTM的最优参数集,从而更好地提高模型预测精度。

1 研究方法

1.1 数据预处理

数量级的差异会导致较大数量级的属性占据主导地位,并且迭代收敛速度缓慢。对数据进行预处理,以消除具有不同量纲的影响,选用Z-Scores标准化处理,变换后的数据均值为0,标准差为1,如式(1)所示。

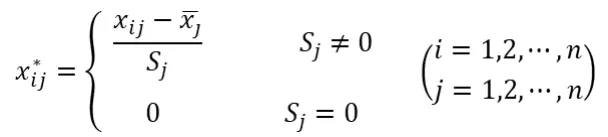
(1)

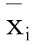
1.2 特征选择

1.2.1 相关分析

相关分析是探究具有特定相似关系的变量之间的相关程度和方向,研究变量之间是否存在一定的相似关系。相关分析的研究主要是研究两个变量之间的密切程度,是研究随机变量的一种统计方法。Spearman秩相关系数是一种非参数度量,用于数据在两个变量之间不是正态分布时。它被定义是两个等级随机变量之间的Pearson相关系数,记录着每个数据点的正等级和负等级之间的差异,如式(2)所示。

(2)

其中,di是xi和yi的秩次差。

1.2.2 系统聚类方法

R型系统聚类方法是将差异较大的变量分离出来,将相似的变量聚在一起。可以从相似的变量中选择出具有代表性的变量,以达到减少变量数量和降维的目的。本文采用的R型聚类方法是凝聚聚类方法。凝聚聚类的过程如下:首先,每个观测到的个体被分成一个类别,然后根据组间平均链锁距离法测量所有个体之间的亲密程度,将亲近的个体分成一个小簇。接下来,再次测量剩下的观察个体和子类之间的亲密程度,并将当前亲密的个体和子类归为一个簇。上述过程重复进行,直到所有个体组合在一起,形成最大的簇[9]。R型聚类方法的流程图[10]如图1所示。

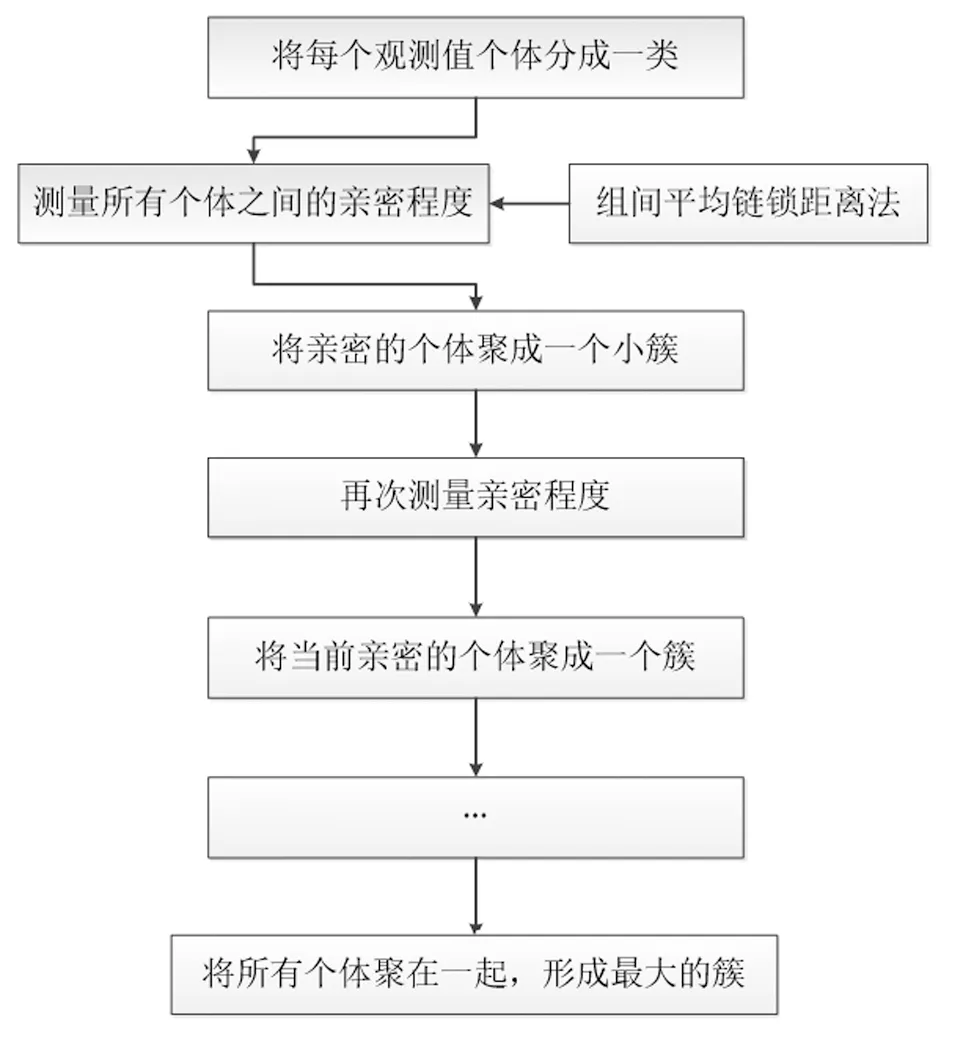
图1 R型聚类方法流程图

1.3 粒子群算法优化LSTM预测模型

长短期记忆神经网络预测模型包含着许多网络参数,如核函数、学习率和神经元数量等,这些参数都会影响LSTM模型的预测精度,因这些参数过分依赖于经验设置致使其预测精度不稳定。与此同时,随着参数设置的不同,LSTM模型的训练时间长度也会发生变化。利用粒子群算法对LSTM模型的部分网络参数进行搜索,可以解决人工选择参数的问题。针对人工参数设置导致模型的精度低、泛化能力弱等问题,本节采用搜索范围广、收敛速度快的PSO算法对LSTM的一些超参数进行优化,构建PSO-LSTM模型,寻找到LSTM的最优参数集,从而更好地提高模型预测精度。PSO-LSTM模型流程图如图2所示。

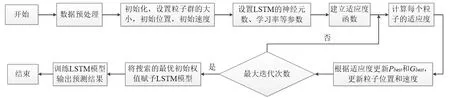
图2 PSO-LSTM模型流程图

PSO-LSTM 预测模型构建的具体操作步骤如下:

步骤1:数据预处理。对变量数据进行采集,通过数据预处理得到模型的训练集与测试集。

步骤2:参数初始化。对PSO的参数进行初始化,比如学习因子、迭代次数、粒子数量等参数。与此同时,对LSTM中的学习率、时间步长、批处理量、隐藏层单元数等参数寻优范围进行设置。

步骤3:评价粒子。把测试集在 LSTM 模型中得到的真实值和预测值间的MAE和RMSE的平均值当作粒子适应度值。将得到的值和初始值Pbest、Gbest进行比较,得到最优的Pbest、Gbest。

步骤4:对粒子的位置和速度进行更新。

步骤5:判定终止条件。如果迭代次数达到了预设值,那么停止搜索,输出得到最优参数组;如果未达到,那么返回到步骤3进行迭代寻优。

粒子群优化算法在初始化粒子的速度和位置后,通过不断地迭代更新自身的位置来得到模型最优解。PSO算法对于多维空间函数优化和多目标优化具有鲁棒性好、收敛速度快等优势,适用于神经网络中某些超参数的优化,为模型组合提供了理论依据[]。经过粒子群算法优化后的PSO-LSTM预测模型通过不断迭代,在给定参数范围内搜索到参数的最优值,达到了最佳的预测效果。

1.4 布谷鸟算法优化LSTM预测模型

针对人工设置参数设置导致模型的精度低、泛化能力弱等问题,本节采用具有很好的全局和局部的搜索能力、收敛速度较快的CS算法对LSTM的一些超级参数进行优化,构建CS-LSTM模型,寻找到LSTM的最优参数集,从而更好地提高模型预测精度。CS-LSTM模型流程图如图3所示。

图3 CS-LSTM模型流程图

CS-LSTM 预测模型构建的具体操作步骤如下:

步骤1:数据预处理。对变量数据进行采集,通过数据预处理得到模型的训练集与测试集。

步骤2:参数初始化。对CS的参数进行初始化,比如学习因子、迭代次数等参数。与此同时,对LSTM中的学习率、时间步长、批处理量、隐藏层单元数等参数寻优范围进行设置。

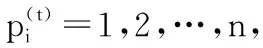
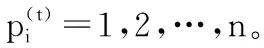
步骤5:将上代的最优适应度函数值做比较,更新得到该代的最优解的位置Gbest。对算法是否满足收敛条件进行判断,如果满足收敛条件,输出最优的位置Gbest;否则,跳转回到步骤4,重复优化迭代,直至完成L次迭代。

步骤6:判定终止条件。如果满足终止条件,那么停止搜索,输出得到最优参数组;如果未达到,那么返回进行迭代寻优。

1.5 预测性能评价指标

为了更加全面地、准确地评估模型的预测效果,本文主要选取决定系数(R2)、平均绝对百分比误差(MAPE)、均方根误差(RMSE)和平均绝对误差(MAE)四个指标作为模型评价指标,计算公式如下[12]:

1.5.1 决定系数

R2即决定系数,是衡量预测值对真实值拟合好坏的程度。R2的范围在(0～1)之间,越接近1,说明模型拟合的越好。

1.5.2 平均绝对误差

平均绝对误差可以通过直接计算残差的平均值得到,其表示的是预测值和观测值之间的绝对误差平均值。平均绝对误差是一种线性分数,其中所有观测值个体差异都在平均值上加权。计算公式如式(3)所示。

(3)

1.5.3 均方根误差

均方根误差是有数据的估计值和真实值之差在求取平方后得到的期望值的平方根。均方根误差是指每个数据偏离真实值的距离平方和后计算平均值再开方。其指标越小,表示精度越高。计算公式如式(4)所示。

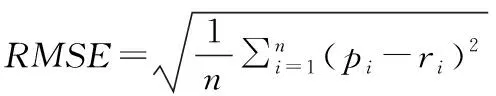
(4)

1.5.4 平均绝对百分比误差

平均绝对百分比误差得到的是百分比值,即相对误差损失的期望值,是绝对误差与真值的百分比。在模型预测中,平均绝对百分比误差值越小,说明模型的精度越好。计算公式如式(5)所示。

(5)

其中,n是样本的个数;ri是实际值;pi是预测值。

2 案例分析

2.1 催化裂化流程介绍

以某石化企业催化裂化装置吸收稳定系统为例,采集了两年347 520个观测值数据,数据每3 min收集一次。对于系统的不同部分,收集时间相同。催化裂化装置吸收稳定系统流程图如图4所示,系统包括吸收塔C-101、解吸塔C-103、再吸收塔C-102、稳定塔C-104等。FEED1为粗汽油,FEED2为高压富气。OUT1为干气,OUT2为富吸收性油,OUT3为液化气,OUT4为稳定汽油。

吸收稳定系统是催化裂化过程的重要组成部分。它的主要任务是将工艺产生的粗汽油和高压富气分离成干气、液化气、稳定汽油等产品。同时尽可能降低干气中C3及以上重组分的含量,保证液化气体和稳定汽油满足产品质量要求。该系统主要由以下设备组成:吸收塔、解吸塔、重吸收塔、稳定塔等。吸收过程的状态对整个装置的良好运行至关重要。解吸塔的运行对吸收稳定系统的运行有很大的影响。过度的解吸不仅会导致冷凝油罐液位上升,还会导致解吸塔热源的浪费,大量的解吸气体重新进入风冷和水冷。同时,吸收塔的负荷也会增加,装置的能耗也会大大增加。解吸不足会导致稳定塔压力过高,影响稳定塔的正常运行。解吸效果与解吸塔底再沸器返回温度有很大关系,该温度的控制是通过调节热源控制阀来实现的。

2.2 解吸塔底再沸器返塔温度主要相关变量数据预处理

在催化裂化的整个过程中有很多变量。本文只考虑与解吸塔底再沸器返塔温度有关的变量。通过专家经验选择了19个变量。采用Z-Scores标准化处理,消除了量纲不同带来的影响。转换后的数据标准差为1,均值为0。

2.3 解吸塔底再沸器返塔温度主要相关变量特征选择

TIC3003与其相关变量间的Spearman秩相关系数值如表1所示,TIC3003相关变量之间R型聚类结果如图5所示。

表1 TIC3003相关变量列表

通过表1中TIC3003与其相关变量间的Spearman秩相关系数值和图5中TIC3003相关变量之间R型聚类结果,直观地反映了解吸塔底再沸器返塔温度与其相关变量之间的关系。从图5中的纵坐标可以看出变量之间的聚类顺序,结合TIC3003与其相关变量间的Spearman秩相关系数值结果、TIC3003相关变量之间R型聚类结果及专家经验,经过特征选择和提取,共得到10个变量,如表2所示。通过特征选择和提取,数据变量被有效降维。

表2 特征选择后的TIC3003主要相关变量列表

2.4 解吸塔底再沸器返塔温度预测案例

在主要控制变量解吸塔底再沸器返塔温度的预测中,选用经过特征提取与选择后的9个变量为输入变量,如表2所示。在对正常工况F类的预测中,选用2 400个连续时间序列数据组成,分别包括有2 000个数据用于训练集,400个数据用于测试集。TIC3003测试集在不同指标下的预测结果评价如表3所示。

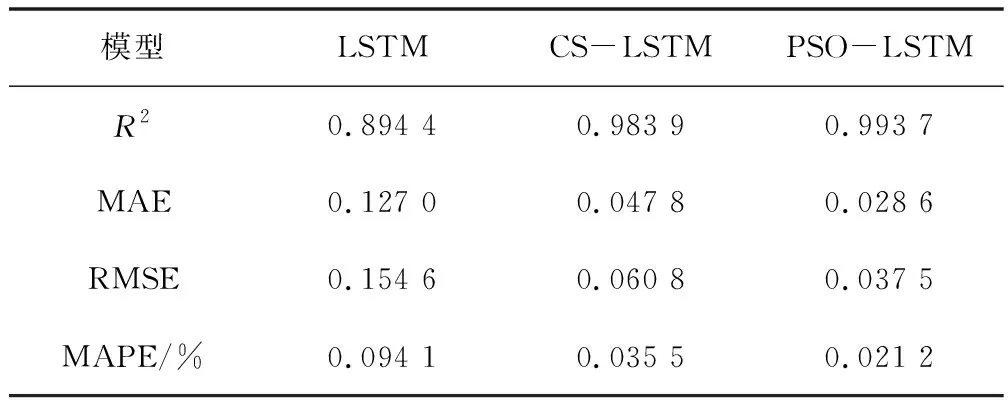
表3 不同指标预测结果评价

如表3所示,TIC3003的预测结果中,TIC3003的预测结果中,PSO-LSTM模型和CS-LSTM模型的训练集、测试集都得到了很好的预测结果,PSO-LSTM模型预测值曲线和真实值之间接近重合,PSO-LSTM模型的R2值为0.993 7,MAE值为0.028 6,RMSE值为0.037 5,MAPE值为0.021 2%,得到了很好的模型预测结果。在与LSTM模型的预测结果比较中,R2指标平均提高11.38%;CS-LSTM模型预测值曲线和真实值之间也接近重合,CS-LSTM模型的R2值为0.983 9,MAE值为0.047 8,RMSE值为0.060 8,MAPE值为0.035 5%,R2指标平均提高9.50%,得到了很好的模型预测结果。在不同模型的预测结果比较中可以看出,PSO-LSTM模型的预测结果更优异,误差更小。