基于动态贝叶斯网络的液压系统可靠性研究
2023-11-09钱存华花飞
钱存华,花飞
(南京工业大学经济与管理学院,江苏南京211816 )
0 前言
液压系统是以液压油为介质,通过操纵控制系统及相关构件,利用油液的压力作用到执行系统上工作的机械装置[1],在油田化工、机械制造、交通运输、建筑工程等方面都有广泛的应用。开放式液压系统在机械化工等工业领域主要用来提供较大的机械力,关系到企业生产安全和效率,其组成结构复杂,检修难度大且维修成本高[2]。若能对液压系统中潜在的故障进行事前预防或者事后快速准确识别,将有效降低故障发生概率并且节约维修时间及费用[3]。因此,液压系统可靠性评估对企业生产的安全性和经济性具有十分重要的现实意义。
贝叶斯网络模型被广泛应用于系统可靠性研究中:罗小芳等[4]通过贝叶斯网络模型分析半潜式钻井平台钻井设备系统的可靠性;陈长飞、白国强[5]基于贝叶斯网络对不同启泵方式的消防系统进行可靠性分析;陈东宁等[6]利用贝叶斯网络分析多性能、多故障状态液压驱动系统的可靠性问题;MARTZ等[7]探究贝叶斯方法在串联系统以及串并联混合系统中健康状态评估的应用。但在实际应用中,贝叶斯网络的构建复杂,计算量大,通过故障树的映射关系转换能有效解决此问题,因此,HACENE、HAMZA[8]就系统可靠性和安全性分析了贝叶斯网络对于故障树的优势;陈喜峰等[9]运用桶消元法简化的贝叶斯网络结合故障树模型理论研究智能电能表的可靠性。贝叶斯网络主要针对的是静态系统,无法描述液压系统可靠性在运行过程中随时间推移的变化情况,并且系统的可维修性更是无法体现。动态贝叶斯网络作为建立在静态贝叶斯网络和隐马尔可夫模型[10]基础上、具备反推理功能的图结构模型,不仅可以描述因素间的逻辑关系和敏感程度,而且加入时间维度理论,可以很好地描述液压系统可靠性随时间的动态演变情况。
鉴于此,本文作者将故障树与动态贝叶斯网络相结合构建液压系统的可靠性分析模型,通过故障树映射关系构建动态贝叶斯网络,利用动态贝叶斯的推理功能评估液压系统在一段时间内的可靠度和可用度变化情况,并且分析液压系统中各部件的故障发生概率,找出系统中容易发生故障的组成部件,以此制定有针对性的检修和维修策略,提升液压系统的可靠性。
1 DBN简介及建模
1.1 动态贝叶斯基本原理
贝叶斯网络(Bayesian Network,BN)是描述一系列变量联合概率分布函数的结构模型,是由根节点、中间节点以及叶节点通过有向边连接构成的无环图。其模型如图1所示,连接变量节点的有向边代表节点间的结构关系,变量节点间的关联强度则通过条件概率体现。
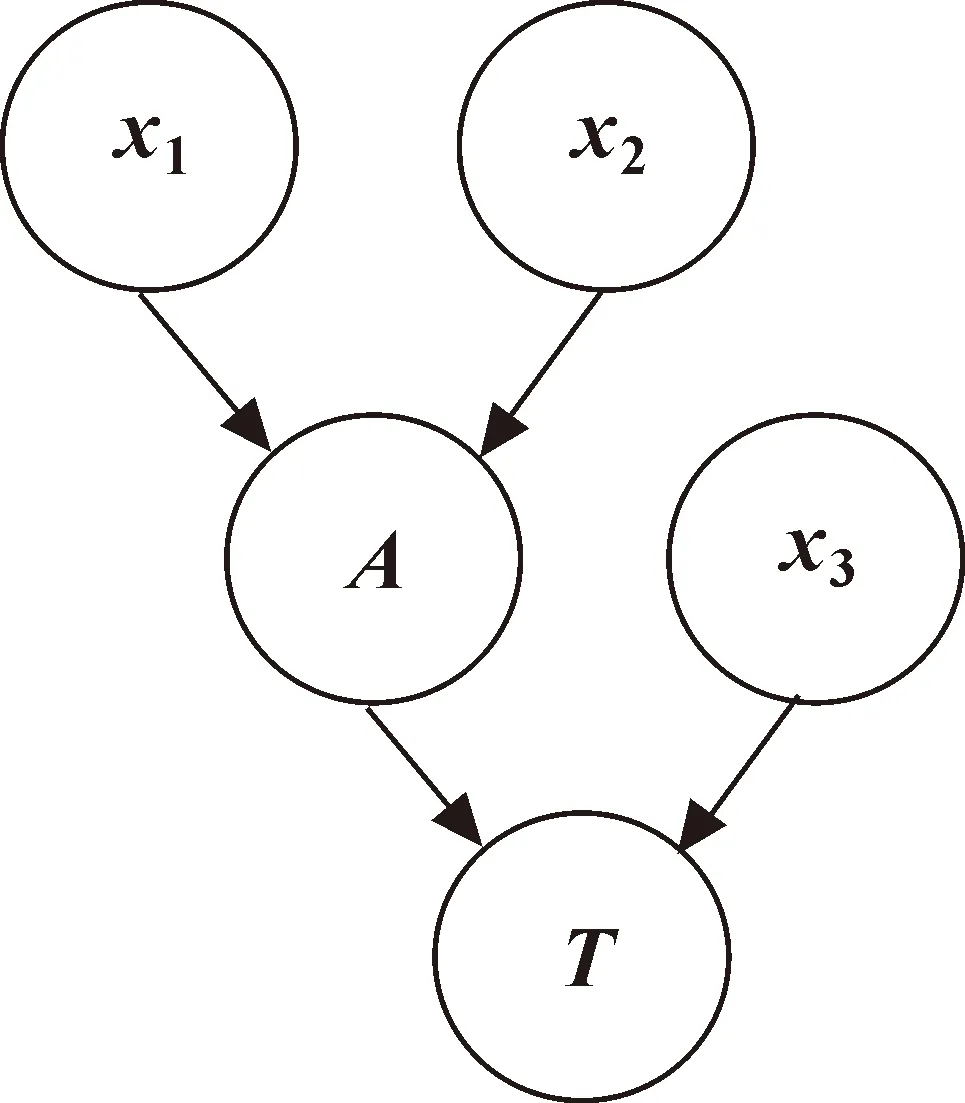
图1 BN模型
动态贝叶斯网络(Dynamic Bayesian Network,DBN)是结合静态贝叶斯网络以及时间维度理论构建的联合概率分布模型,不仅可以描述变量节点间的关系,而且还可以描述变量概率分布随时间推移的变化情况。DBN可定义为(G1,G→),其中:G1是确定了先验概率的初始贝叶斯网络;G→是转移网络,包含了两个相邻时刻的BN。其概率分布P(Xt|Xt-1)如公式(1)所示:
(1)
其中:xt,i为第t个时刻的第i个节点;πt,i为第t个时刻的第i个节点的父节点;N为该DBN中的节点数。
通过对两个相邻时刻BN的延伸,便可以得到具有T个时间片的动态贝叶斯网络,其联合概率分布公式如式(2)所示:
(2)
1.2 动态贝叶斯网络建模
在动态贝叶斯网络模型中,造成系统故障的因素源可由根节点表示,因素源的状态可由节点属性表示,而且因素源之间的逻辑关系通过条件概率表示,所以动态贝叶斯网络模型可再现风险传递过程。DBN模型的构建包括结构学习和参数学习两个部分。结构学习包含初始贝叶斯网络和转移网络的建立;而参数学习需要确定初始网络中根节点的初始概率以及设置转移网络中的条件概率。贝叶斯网络模型的构建是以风险故障树为基础,两者存在映射关系,贝叶斯网络模型中的根节点与故障树中基本事件相对应,各节点间的逻辑关系是以故障树中逻辑门和事件间的关系得到的[11]。此外,由于DBN引入时间维度理论,DBN中各节点的顺序需要根据故障树中对应的基本事件的先后顺序确定。具体的映射转换规则如图2所示,A(t+Δt)、B(t+Δt)、T(t+Δt)分别为节点A、节点B和节点T在时间点t+Δt的概率分布情况,随着时间片段的延伸,便可以得到多个时间片段内的动态贝叶斯网络模型。
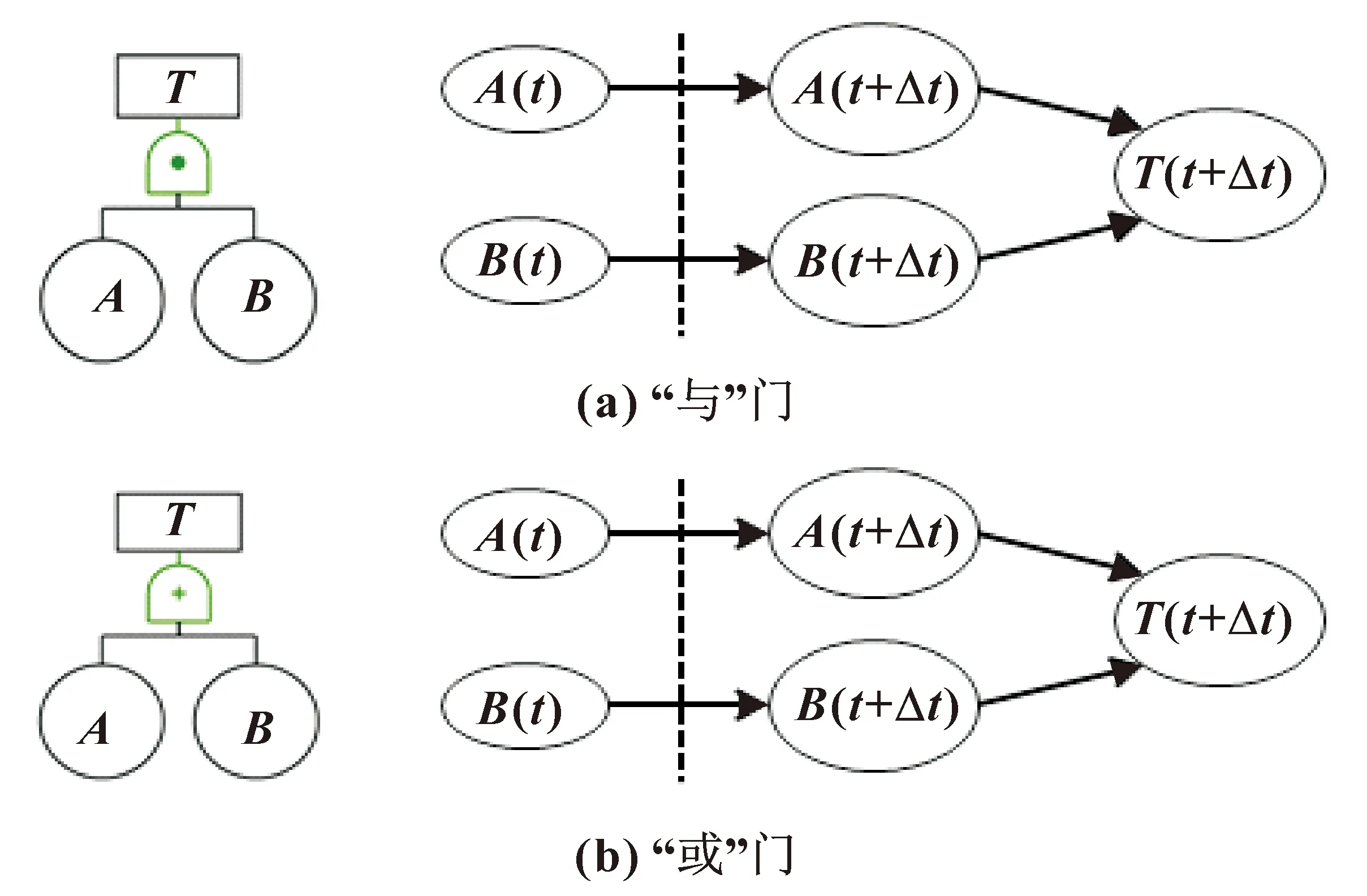
图2 FTA逻辑门的DBN转换规则
2 液压系统DBN模型
2.1 液压系统研究框架
液压系统可靠性研究模型包括液压系统结构以及相关数据处理、液压系统故障树构建以及液压系统动态贝叶斯网络模型分析3个部分[12]。通过对液压系统组成部件、部件间的结构关系以及运行的历史数据整理分析,根据系统构件间的逻辑关系构建液压系统故障树模型,依据故障树与贝叶斯的映射转换规则建立液压动态贝叶斯网络模型进行风险评估,得出系统可靠度和可用度随时间的动态变化情况和各部件故障发生概率,并以此制定相关的预防策略和维修措施。研究模型如图3所示。
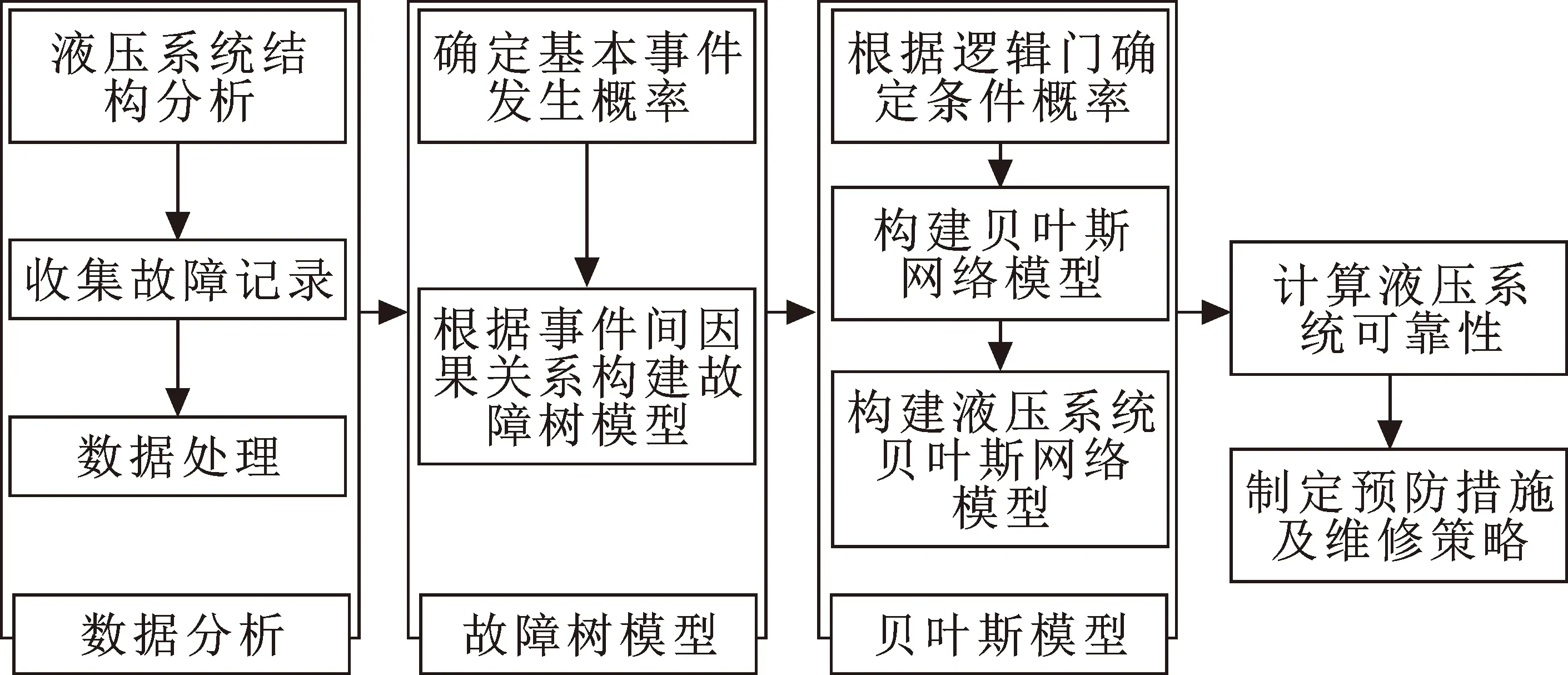
图3 液压系统可靠性研究框架
2.2 液压系统故障树模型
在调研相关文献与资料的基础上,确定以开放式液压系统为例进行研究。开放式液压系统主要由动力系统、执行系统、控制系统、辅助系统4个部分构成,而每个部分又由独立的部件构成,且所有的子系统与部件都是以串联的形式连接,都有着不可替代的作用[13]。因此,系统中任何一个部件的损坏都会导致整个液压系统失效。在故障树模型中,液压系统失效用T表示,将造成液压系统失效的构件以及子系统分别用基本事件Xi和中间事件Yi表示,并且由于串联的形式,各事件间的逻辑关系均用“或”门连接,构建的液压系统故障树模型如图4所示。
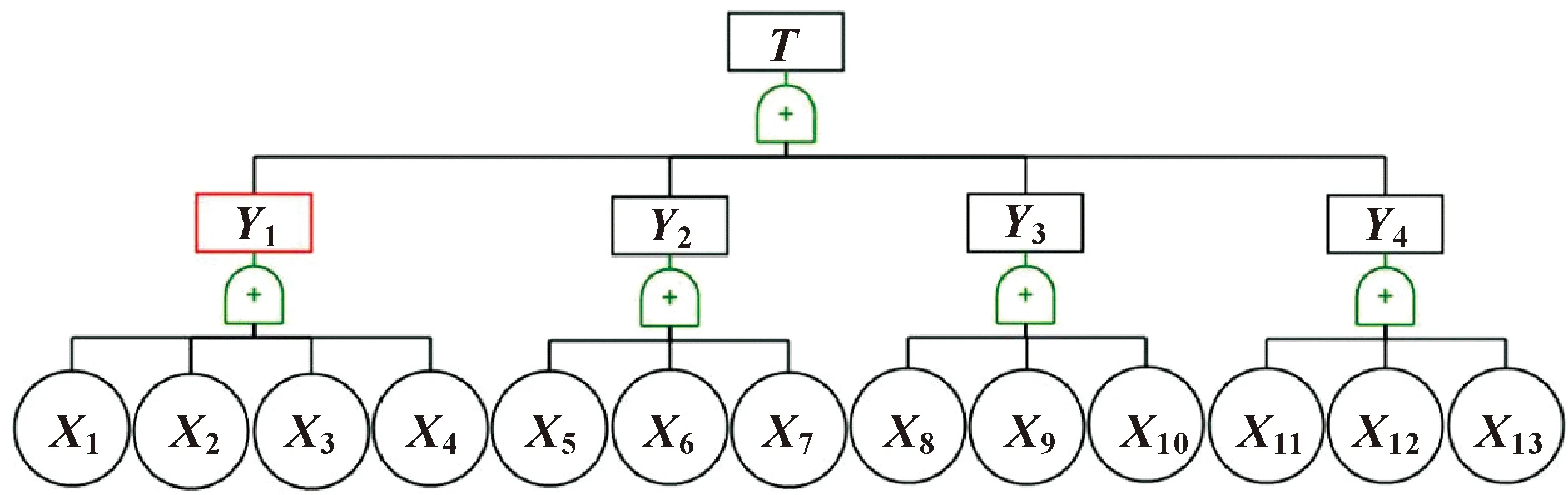
图4 液压系统故障树模型
2.3 DBN模型结构学习
由于液压系统的运行是一个动态的过程,各系统以及构件的可靠性都会随着时间的推移而发生变化,因此需要动态贝叶斯网络模型进行模拟。考虑到动态贝叶斯网络模型连续型变量的复杂性以及液压系统运行的实际情况,本文作者对液压系统进行了划分,使得模型中节点变量离散化,简化问题。DBN模型结构的学习以液压系统故障树模型为基础,运用图2的映射规则转换,构建的液压系统动态贝叶斯网络拓扑图如图5所示,其中,为描述DBN模型的动态性,建立了两个相邻时间片段间的转移网络,通过根节点Xi当前时刻产生的结果对下一个时刻自身产生的影响体现。
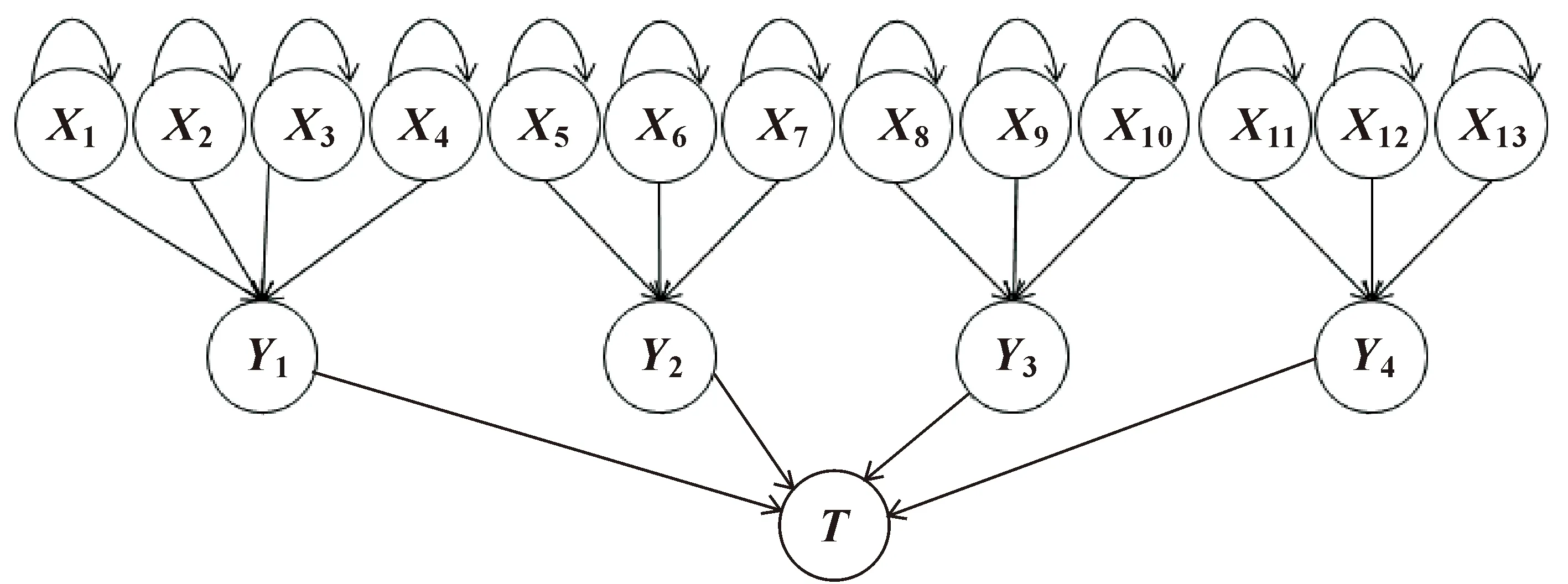
图5 液压系统可靠性DBN模型
2.4 DBN模型参数学习
根据液压系统的实际情况,将前文故障树中各基本事件状态转换到液压系统动态贝叶斯网络模型中的对应根节点,液压系统各部件的失效率λ(月-1)以及维修率μ(h-1)数据来源于可靠性手册《IEEE STD-493》,文中部件失效名称以及选取的参数如表1所示。
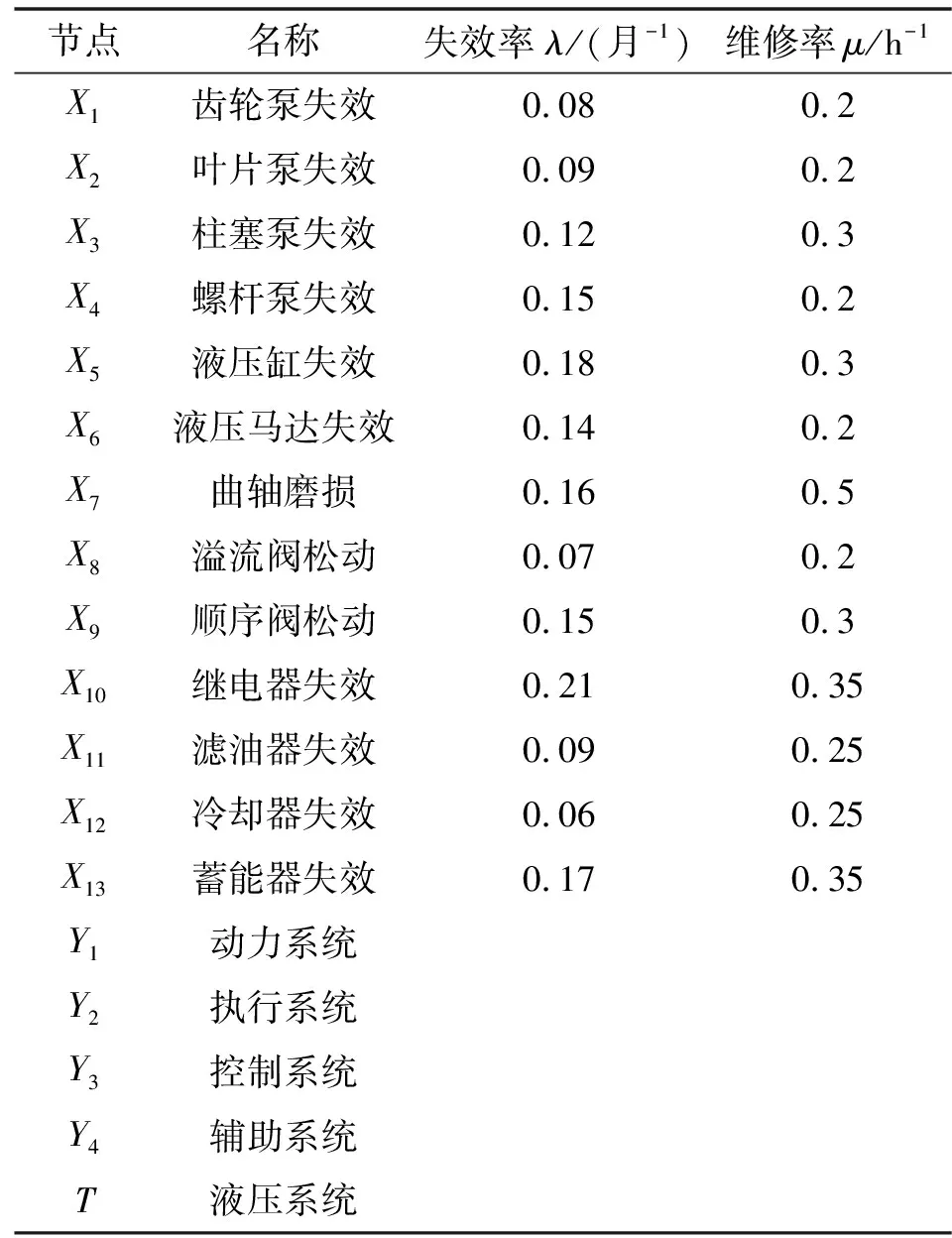
表1 风险因素基本参数
文中假设液压系统及其各组成部件均只存在“正常运行”和“设备故障”两种状态,分别用“0”和“1”表示。且设定液压系统运行时间以及维修时间均服从指数分布,则得到故障发生概率密度函数为fi(t)=λie-λit,以及故障发生后设备维修概率密度函数为gi(t)=μie-μit,通过图2的转化规则可以得到根节点Xi条件概率表达式如公式(3)所示:
(3)
其中:Δt取值为1个月;λ和μ取值如表1所示。文中研究涉及是否考虑维修因素两种情况下液压系统可靠性的比较分析,对于不考虑维修因素的液压系统,μi=0,则系统中某一部件发生故障后,下一时刻此部件仍有故障的概率为1。通过构建的动态贝叶斯网络结合先验概率,便可计算出系统中各部件的故障概率。
3 液压系统可靠性分析
液压可靠性研究主要分析液压系统中各子系统以及部件在一段时间内的运行情况,运用GENIE软件进行建模[14],实现液压系统运行的动态模拟。假设在t=0时刻,所有部件均正常运行,即P(Xi=0)=1时,系统运行一段时间后,通过DBN推理功能可以得出液压系统可靠度及可用性随时间推移的变化情况以及液压系统中各部件的故障概率,确定系统中容易发故障的组成部件,进而评估液压系统的可靠性。
3.1 可靠度分析
对于未考虑维修因素的液压系统动态贝叶斯网络模型,在t=0时刻,液压系统正常工作,运行一段时间后便可得到系统可靠度随时间推移的变化情况。文中模拟液压系统正常运行10个月,在这期间,系统可靠度随时间的推移而逐渐降低,并且下降的速率很快,在较短的时间内趋于0,结果如图6所示。其中,动力系统、执行系统、控制系统、辅助系统4个子系统的可靠度也均随着时间的推移降低,并且不同子系统可靠度下降的速率不同。执行系统可靠度降低速率最快,对液压系统可靠度的影响程度最大,其次是辅助系统和动力系统。因此在日常维护工作中,需要根据各子系统可靠度变化规律制定有针对性的检修策略,重视执行系统。
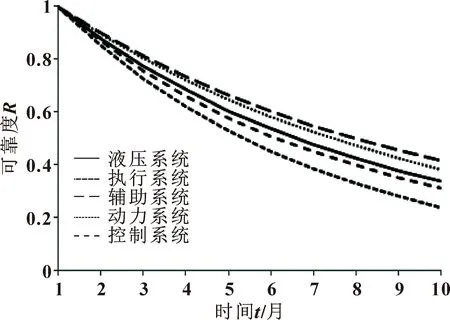
图6 液压系统可靠度变化曲线(不考虑维修因素)
对于考虑维修因素的液压系统动态贝叶斯网络模型,采取同样的初始数据模拟,得到结论是液压系统可靠度也会随时间的推移呈现下降趋势,但下降的速率明显有所减缓,最终会在较高的水平趋于稳定,如图7所示。对比两种情况下可靠度变化规律,可知日常的维护和检修对保障液压系统的可靠性有重要的作用。
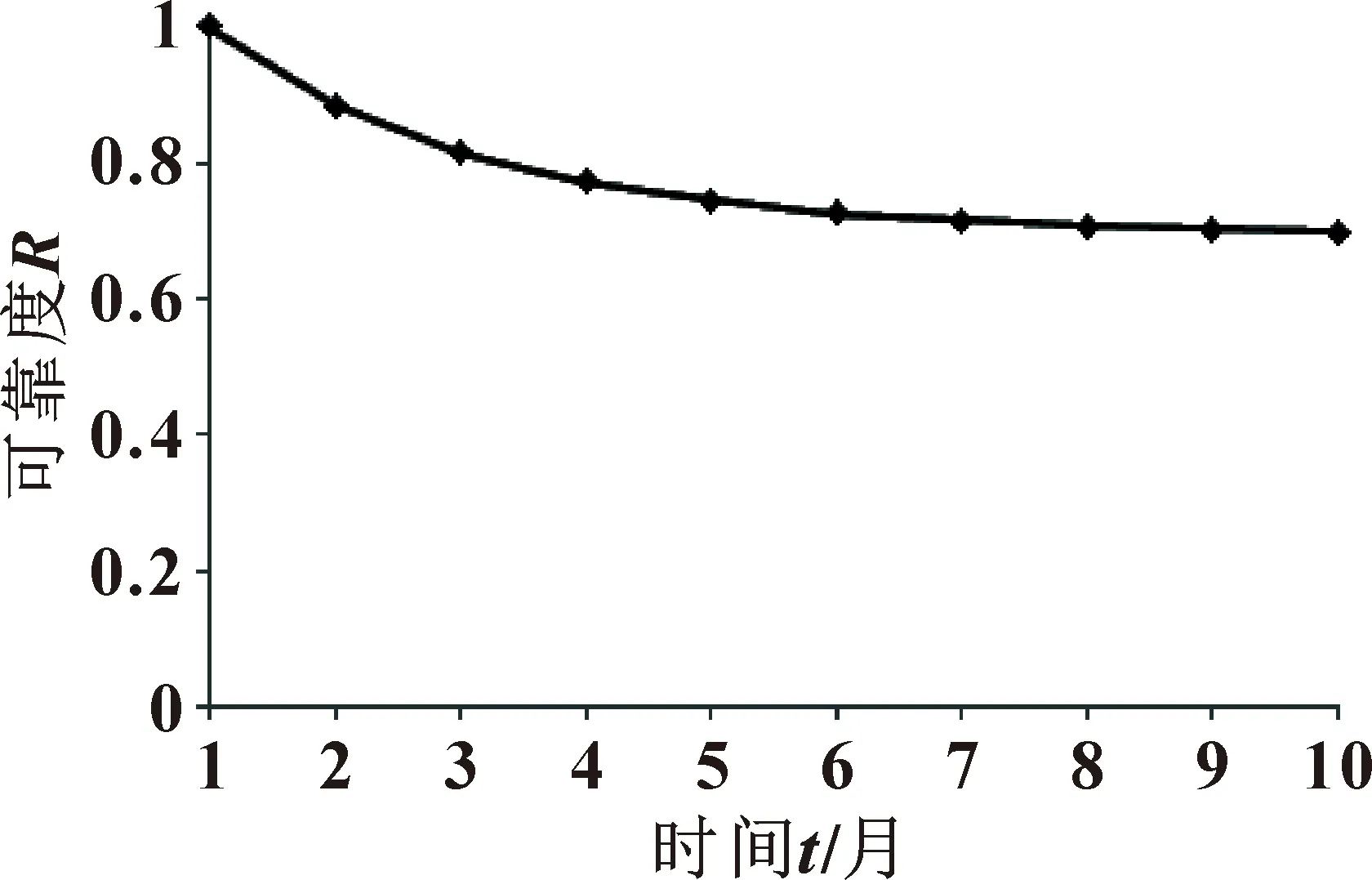
图7 液压系统可靠度变化曲线(考虑维修因素)
3.2 可用度分析
在考虑维修因素的液压系统动态贝叶斯网络模型中,考虑液压系统的运行过程,设备的平均维修时间为2 h。在t=0时刻,液压系统处于正常工作状态,运行一段时间后便可得到系统可用度随时间推移的变化情况。在系统刚开始运行的短时间内,液压系统的可用度会呈现下降趋势,但引入维修因素后,系统的可用度在21 h后逐渐趋于稳定,其值约为0.975 368 635,结果如图8所示。往复式液压系统在实验过程中具有较高的可用度,但设备在现实工作的情况下,可能会因为工作环境、使用方式、维修策略的不同,进而导致液压系统的可用度发生变化。
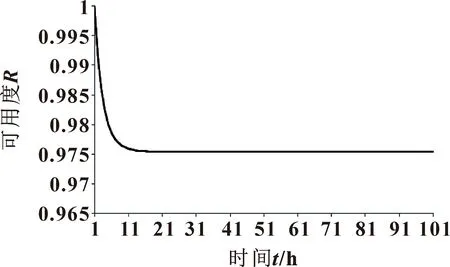
图8 液压系统可用度变化曲线
3.3 后验概率
通过分析液压系统中各部件的后验概率,可知它们在系统中发生故障的可能性,进而确定关键的结构部件。采用贝叶斯网络的逆向推理功能进行故障诊断,分析液压系统失效P(T=1)的情况下,各部件发生概率情况[15]。后验概率计算表达式如公式(4)所示:
(4)
其中:T表示液压系统发生失效;Xi表示发生故障的节点;N表示根节点个数。
文中将液压系统在t=0时刻,所有部件正常工作的前提条件下运行一个月后的各部件故障概率作为先验概率,然后利用贝叶斯的逆向推理功能得到各部件的后验概率,即P(Xi(t)=1|T(t)=1)=1,相关参数如表2所示,可以看出在所有子系统中,执行系统失效的概率最高。这是由于系统中液压缸、液压马达和曲轴等部件一直处于高频率工作,容易发生失效现象。此外,在辅助系统中,蓄能器发生故障的概率也较高,所以在日常检修和维修中可以从执行系统部分开始检查。
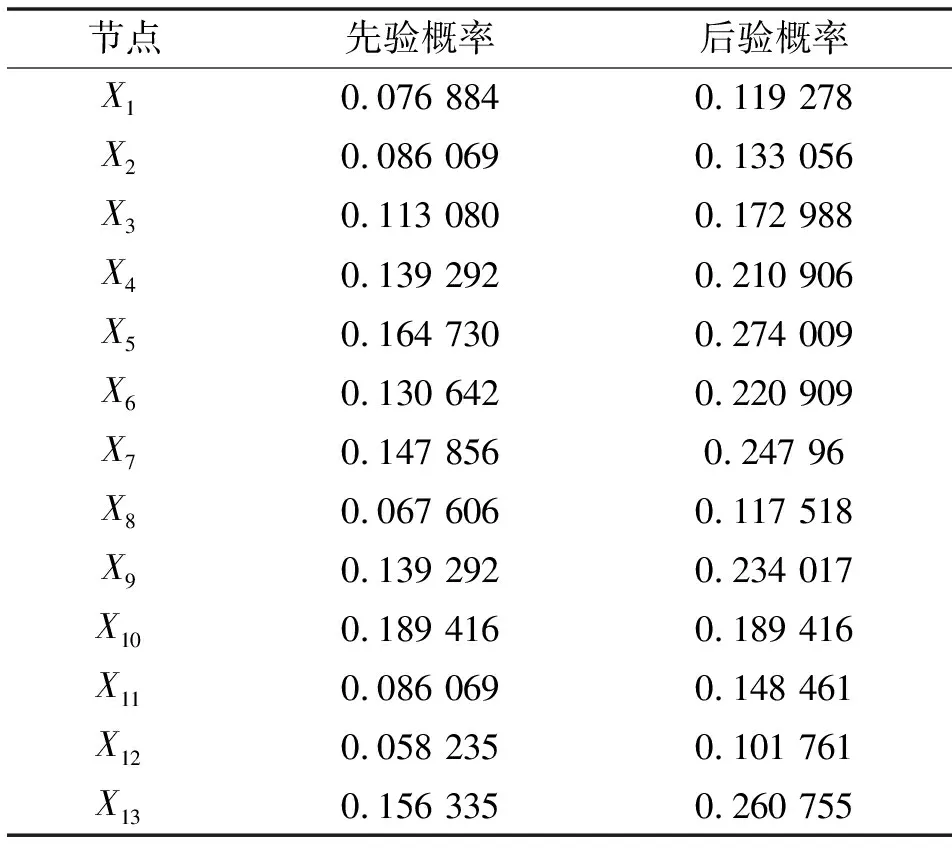
表2 后验概率
3.4 灵敏度分析
在动态贝叶斯网络模型中,根节点先验概率变化会对液压系统故障发生概率产生影响,但不同的根节点相同概率变化率引起的液压系统故障发生概率变化程度不一样,这一程度可以用敏感度衡量,计算公式如式(5)所示:
|P(Pk=pk|Sk=sk)-P(Pk=pk|Sk=0)|
(5)
其中:N表示系统中根节点的数量;sk表示根节点Sk的状态。当节点Pk处于pk状态下,便可得到根节点Sk的敏感度。
由文中液压系统动态贝叶斯网络模型中各节点的相关参数均由零件失效率和维修率计算得出,敏感度可以通过调整零件的输入参数得到,所以假设系统中零件失效率存在不确定性,其值设定为10%[16],利用GENIE软件可以实现敏感性分析,分析结果如图9所示。可以看出执行系统仍是最容易失效的子系统,其中的液压缸失效、液压马达失效和曲轴失效都是液压系统中的敏感风险源。此外,敏感度分析得出的结论与逆向推理结论一致,进一步论证了文中液压系统动态贝叶斯网络模型的正确性。
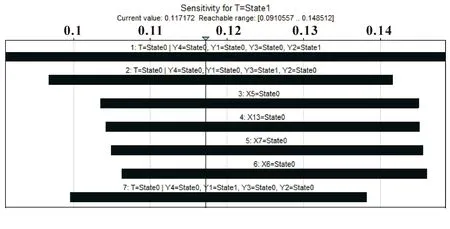
图9 液压系统灵敏度分析
3.5 DBN 模型验证
对建立的液压动态贝叶斯网络模型进行验证分析。液压系统从t=0时刻开始,正常工作1个月后,考虑未考虑维修因素和考虑维修因素的部件X1故障发生概率均为0.076 884,模型运行4个月之后,对于未采取维修措施的液压系统,部件X1故障发生概率升至0.273 851,系统故障发生概率从0.120 347升至0.394 989;对于采取了预防措施的液压系统,部件X1故障发生概率升至0.207 62,系统故障发生概率从0.117 172升至0.256 273。实验结论均符合DBN模型验证的3条公理,因此文中动态贝叶斯网络模型的可行性得到验证。
4 结论
(1)通过建立的液压系统可靠性研究模型对液压系统失效风险进行全面分析,包括梳理液压系统结构组成,根据部件间的结构关系构建故障树模型,建立动态贝叶斯网络风险评估模型。并以此提出事前预防和事后维修策略,确保研究模型的科学性。
(2)利用映射关系及转换规则将故障树与动态贝叶斯网络相结合应用于液压系统的可靠性分析中,有效弥补故障树法无法描述液压系统运行具有动态特征的缺陷,并且引入了维修因素,使得模型更加贴近现实应用,有效地评估液压系统运行的可靠性。
(3)利用液压系统动态贝叶斯模型的推理功能可以得到液压系统可靠性变化规律:液压系统的可靠度会随时间推移而呈现下降趋势,且下降速率较快,但引入维修因素后,液压系统的可用度可以维持在较高水平,所以定期的检修和维护可以保障液压系统的可靠性。
(4)DBN的推理功能可以实现液压系统故障诊断,找出容易发生故障的部件。实验结果表明:液压缸、液压马达、曲轴和蓄能器是液压系统容易发生故障的薄弱环节,在维修过程中要加以重视。同时后验概率和灵敏度分析结论也验证了文中DBN模型的正确性。
