基于自抗扰控制的分布式铰接车辆转向控制
2023-11-09曹国栋王铁吉志勇马好娜刘兆基
曹国栋,王铁,吉志勇,马好娜,刘兆基
(太原理工大学车辆工程系,山西太原 030024)
0 前言
随着国内外智能驾驶技术的快速发展,为保障矿运车辆安全、可靠地行驶,无人驾驶矿运车辆应运而生。分布式铰接车辆作为矿运车辆的典型代表,具有承载能力高、机动性强、成本低等特点,在实际运输作业中被广泛应用。然而,铰接车辆通过两车体间的相对运动实现转向,转向过程中整车姿态持续变化,因此转向稳定性差、路径跟踪困难。
近年来,为提高铰接车辆路径跟踪控制精度,在深入研究其非线性动力学特性的基础上,发展出多种铰接车辆路径跟踪控制技术,典型的控制方法有比例-积分-微分(PID)控制、模糊控制(Fuzzy Control)、最优控制、模型预测控制(Model Predictive Control,MPC)等[1-2]。文献[3]设计出不依赖铰接车辆精确模型的PID路径跟踪器;文献[4]设计了模糊控制器,并以PID控制器为对照组,进一步缩短了铰接车辆进入稳定转向状态的时间;文献[5]提出基于线性二次型调节器(Linear Quadratic Regulator,LQR)的铰接车路径跟踪控制器,虽然该控制器的鲁棒性较强,但不能适应路径曲率变化较大的路况;文献[6]基于线性化的铰接车辆三自由度动力学模型,应用模型预测控制器对铰接车辆的转向驱动力矩进行控制,提高了车辆在纵向车速恒定状态下的路径跟踪精度,但是没有考虑铰接车辆的非线性动态特性。在建立铰接车辆路径跟踪控制器过程中,通常将液压转向系统等效为转向驱动力矩,很少考虑转向系统自身特性对铰接车辆行驶稳定性的影响。
转向系统的核心是在满足转向稳定性的前提下,灵活改变车辆的行驶方向。由于铰接车辆转向阻力矩较大,通常采用液压转向系统提供转向驱动力矩[7]。文献[8]建立了基于PID控制的双阀控非对称缸液压转向系统仿真模型,并通过试验证明了所建模型的准确性;文献[9]建立了基于二自由度拖拉机动力学模型的液压转向系统模糊控制器,将车辆转向角度误差控制在0.017 rad以内;文献[10]针对液压系统扰动的不确定性,设计了基于模糊滑模控制的全液压转向系统控制器,在一定程度上抑制了转向控制系统的抖动,提高了液压转向系统的鲁棒性。上述文献在建立液压转向系统模型过程中,对流量-压力特性进行了线性化处理,无法反映液压系统的非线性动力学特性;同时,没有考虑前馈控制,不能及时消除系统扰动,降低了液压转向系统的抗扰动性能。
ADRC(Active Disturbance Rejection Control )控制器继承了PID控制器基于误差来消除误差的核心思想,采用扩张状态观测器测量并消除被控对象中的各种非线性干扰后,形成一个积分串联型PID控制器,提高控制系统稳定性[11-12]。铰接车辆转向时受转向阻力矩变化、质心位置偏移和路面不平度等非线性干扰的影响[13-14],可采用ADRC控制器提高车辆的抗扰动性能。
本文作者首先建立包括车身模型、轮胎模型和液压转向系统模型在内的铰接车辆11自由度非线性动力学模型,而后设计了考虑铰接车辆转向时转向阻力矩变化、质心位置偏移和路面不平度等非线性干扰因素的自抗扰控制器(ADRC),最后通过MATLAB/Simulink仿真验证所设计的液压转向控制系统的性能。
1 分布式铰接车辆动力学建模
1.1 车身动力学模型
为研究铰接车辆行驶过程中前后车体各自的运动状态,对其两车体进行如图1所示受力分析。
图中:OXY为绝对坐标系;O1X1Y1为原点固结在前车体质心上的随动坐标系,X1轴与前车体纵向轴线重合;O2X2Y2为原点固结在后车体质心上的随动坐标系,X2轴与后车体纵向轴线重合;ui为车体质心纵向速度(i=1,2);vi为车体质心侧向速度(i=1,2);Fxij为轮胎纵向力(i=1,2;j=1,2);Fyij为轮胎侧向力(i=1,2;j=1,2);Ti为转向驱动力矩(i=1,2);Rx为铰接点处沿车体纵向轴线方向作用力;Ry为铰接点处沿车体侧向轴线方向作用力;γ1为前车体质心处横摆角速度;γ2为后车体质心处横摆角速度;L11为铰接点至前车体质心距离;L12为前车体质心至前桥距离;L21为铰接点至后车体质心距离;L22为后车体质心至后桥距离;Lf为前车体轮距;Lr为后车体轮距。其中:(i=1,2)分别表示前车体和后车体;(j=1,2)分别表示车体左侧和右侧。
铰接车辆两车体质心间的运动学关系为
(1)
依据牛顿-欧拉法对前后车体进行动力学分析可知,前车体和后车体质心处的纵向运动、横向运动和横摆运动的表达式分别为式(2)和式(3):
(2)
(3)
式中:I1、I2分别为前车体和后车体的转动惯量;T1、T2分别为前车体和后车体的转向驱动力矩;m1、m2分别为前车体和后车体的质量。
联立式(1)—(3)可得X=[u1,v1,u2,v2,γ1,γ2]为状态变量、u=[Fx11,Fx12,Fx21,Fx22,Fy11,Fy12,Fy21,Fy22]为输入、Y=[u1,v1,u2,v2,γ1,γ2]为输出的非线性铰接车辆车身动力学模型。
1.2 液压转向系统模型
铰接车辆液压转向系统采用恒压油源,主要由三位四通比例换向阀和两个非对称液压缸组成,结构简图如图2所示。
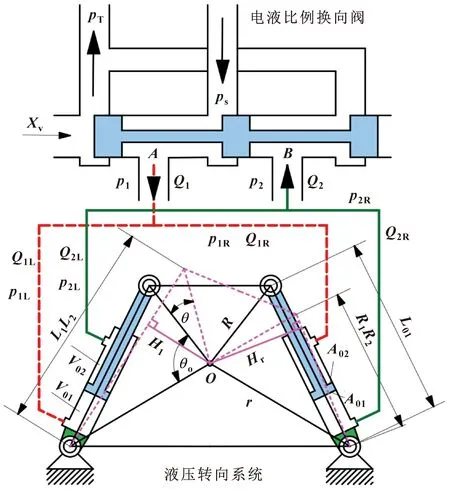
图2 铰接车辆液压转向系统结构简图
图中:ps为液压系统油源供油压力;pT为液压系统回油压力;p1、p2分别为换向阀A口和B口压力;p1L、p2L分别为左侧液压缸无杆腔和有杆腔压力;p1R、p2R分别为右侧液压缸有杆腔和无杆腔压力;Q1、Q2分别为换向阀A口和B口流量;Q1L、Q2L分别为左侧液压缸无杆腔和有杆腔流量;Q1R、Q2R分别为右侧液压缸有杆腔和无杆腔流量;A01、A02分别为液压缸无杆腔和有杆腔工作面积;V01、V02分别为液压缸无杆腔和有杆腔初始容积;θ0为两侧液压缸初始安装角;θ为铰接车转向角度;L01为两侧液压缸初始长度;L1L2、R1R2分别为左侧液压缸和右侧液压缸实时工作长度;R、r分别为铰接点至液压缸与前、后车体连接点距离;Hl、Hr分别为左侧液压缸和右侧液压缸对铰接点O的作用力臂。
液压缸在车体两侧对称布置,通过改变换向阀的阀芯位移,调整液压油流入液压缸的流量和方向,控制车辆转向行驶。车辆转向过程中,液压缸实时长度为
(4)
液压缸活塞杆位移量为
(5)
液压缸作用力臂为
(6)
液压杆位移和铰接角间的运动学关系:
(7)
换向阀A阀口和B阀口的流量分别为:
(1)阀芯位移Xv> 0时,铰接车辆正向转向
(8)
(9)
式中:Cd为流量系数;ω为面积梯度;ρ为液体密度。
(2)阀芯位移Xv<0时,铰接车辆反向转向
(10)
其中:Q1=Q1L+Q1R;Q2=Q2L+Q2R。
铰接车辆转向时,液压缸流量连续方程为
(11)
式中:βe为体积弹性模量;液压缸内泄漏系数Cip和液压缸外泄漏系数Cep取值均为5×10-3;A01=3.10×10-3m2,A02=2.20×10-3m2,V01=4.39×10-4m3,V02=3.42×10-4m3。
转向驱动力矩和液压缸压力之间的关系为
T1=(A01Hl+A02Hr)p1-(A02Hl+A01Hr)p2-
sign(Xv)Tt
(12)
式中:Tt为转向阻力矩。
铰接车辆空载转向时,前车体质量小,以前车体转向为主,转向阻力矩为
(13)
式中:L=L11+L12;L=L11+L12+L21+L22;n为系数;μ为滑动附着系数;Lw为轮胎宽度;f为滚动阻力系数。
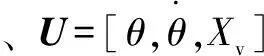
1.3 Fiala轮胎模型
Fiala非线性轮胎模型将胎体与路面之间的相互作用关系简化为弹性梁结构,具有计算量小、通用性强的特点[15]。该模型中的纵向滑移率Sx与纵向力Fx间的关系为
(14)
式中:Kx为轮胎纵滑刚度;Ss为轮胎纵向滑移率;Ssc为轮胎接地印记内纵向滚滑临界点;μ1为复合摩擦因数;Fz为轮胎垂向力。
侧偏角α与侧向力Fy间的关系为
(15)
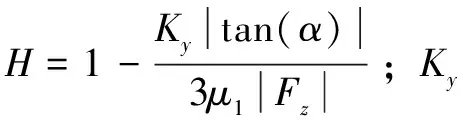
2 ADRC控制器设计
ADRC控制器由跟踪-微分器(TD)、非线性误差反馈控制律(NLSEF)和非线性扩张状态观测器(NLESO)组成。首先应用跟踪-微分器对输入的转向控制信号进行跟踪和滤波,然后应用非线性扩张状态观测器对铰接车辆的运动状态和运动干扰量进行观测,最后将两者的输出信号输送至非线性误差反馈控制律中,经运算后输出液压转向系统控制信号Xv。
2.1 跟踪-微分器
跟踪-微分器的主要作用是快速、无超调地跟踪期望转向角度和期望转向角速度控制信号,并对两控制信号起到一定的滤波作用,降低控制信号的噪声干扰,提高控制信号稳定性。其跟踪算法为
(16)
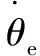
最速综合函数fhan(·)的算法为
(17)
其中:
(18)
(19)
式(18)中:θt为期望转向角度。
2.2 非线性误差反馈控制律
非线性误差反馈控制律为非线性的比例-微分(PD)组合,其控制参数可以在既定的变动范围内进行非线性组合,从而达到更高的控制要求。此算法中应用的非线性函数fal(·)为
(20)
式中:i=1,2,3,4;ai为非线性函数控制参数;di为线性区间的长度。
非线性误差反馈控制算法为
(21)

2.3 非线性扩张状态观测器
ADRC控制器的核心是非线性扩张状态观测器:一方面,通过它可以计算出铰接车辆实际转向角度和转向角速度的观测值,并将结果引入非线性误差反馈控制律中形成闭环控制;另一方面,液压转向系统中的流量、压力、工作温度、机械磨损等内部状态变量和路面不平度、前后车体相对运动干涉等外部状态变量,被统一作为扰动量ω(k),前馈至非线性误差反馈控制律中消除。非线性扩张状态观测器的主要算法为
(22)
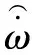
依据上述数学模型,在MATLAB/Simulink中搭建的ADRC控制器如图3所示。
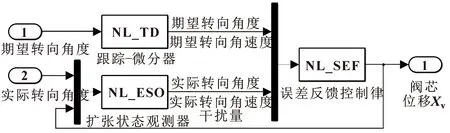
图3 ADRC控制器结构
3 分布式铰接车辆转向特性仿真分析
3.1 整车仿真模型
分布式铰接车辆整车模型主要包括非线性车身动力学模型、非线性液压转向系统动力学模型、非线性轮胎模型和液压转向系统控制器,该模型包括前车体速度闭环控制和整车转向角度闭环控制。在MATLAB/Simulink中搭建的仿真模型如图4所示。
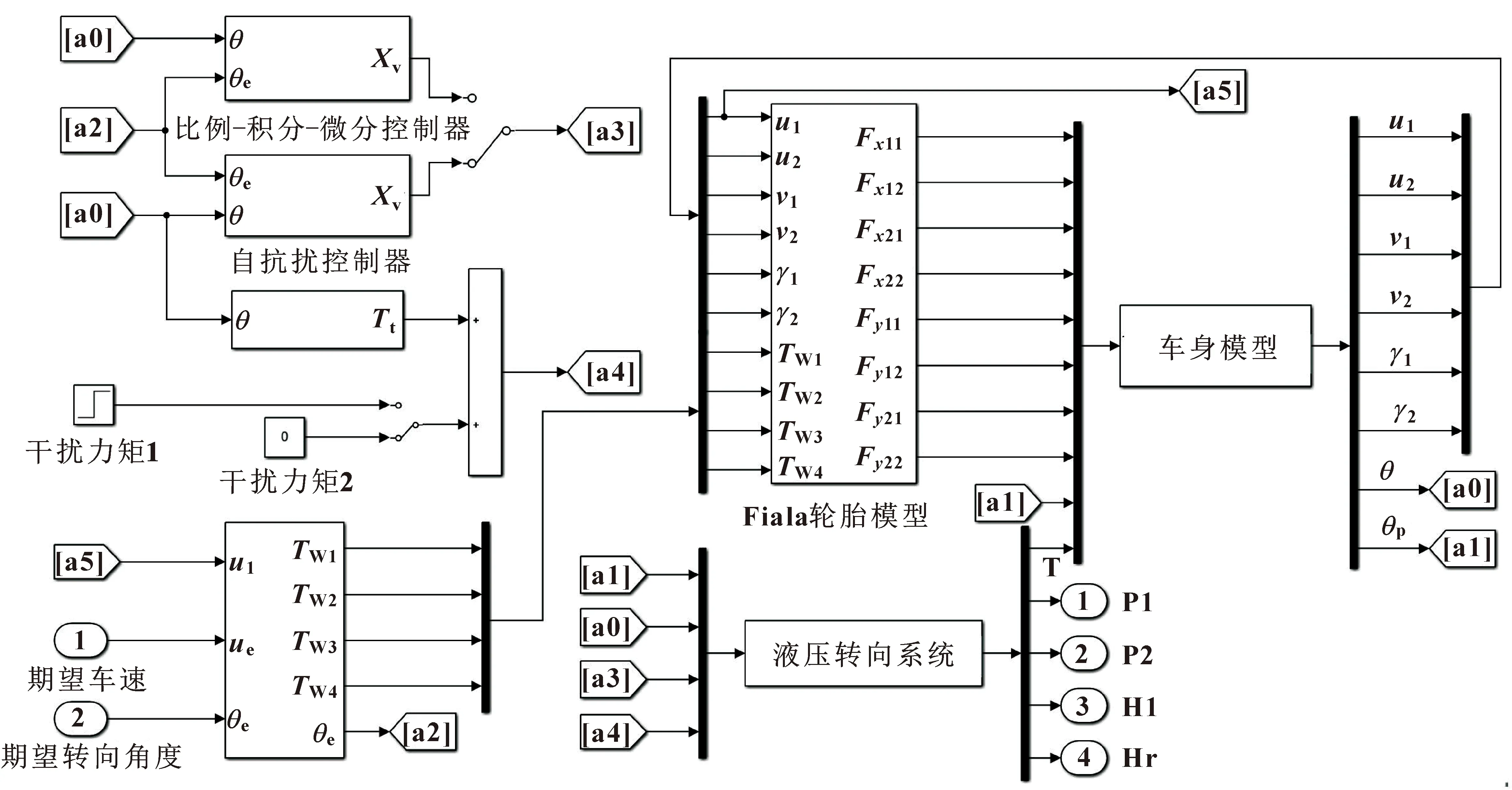
图4 铰接车辆整车仿真模型
3.2 铰接车辆转向特性仿真分析
为验证ADRC控制器在铰接车辆液压转向控制系统中的应用效果,分析铰接车辆的转向特性,基于上述模型,分别采用ADRC控制器和PID控制器作为液压转向系统控制器,进行初始车速为2.5 m/s的转向分析。前车体质心在绝对坐标系中的运动轨迹如图5所示,PID参数取KP=10、KI=0.02、KD=0.02,液压转向系统主要参数如表1所示,ADRC控制器参数如表2所示。

表1 液压系统主要参数
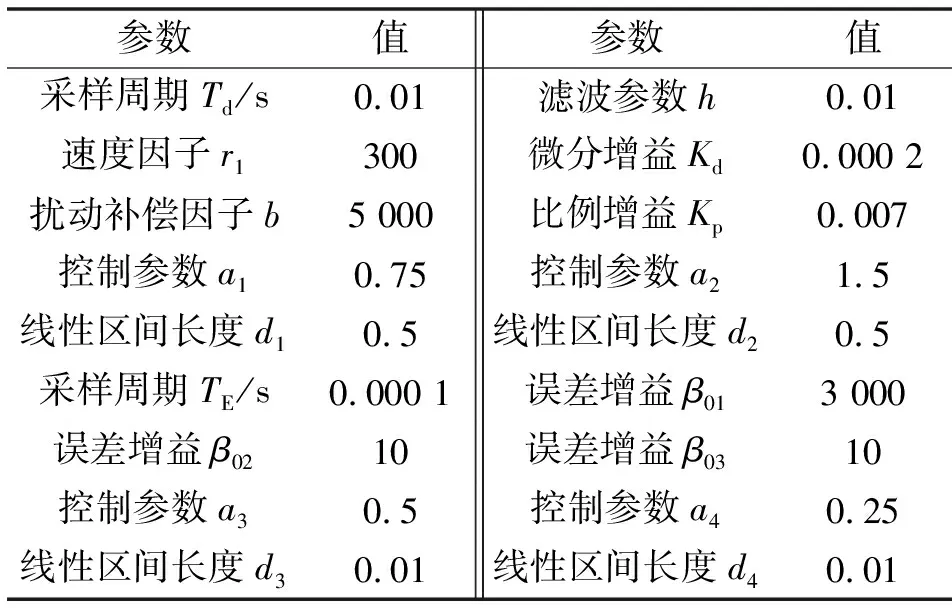
表2 ADRC控制器参数
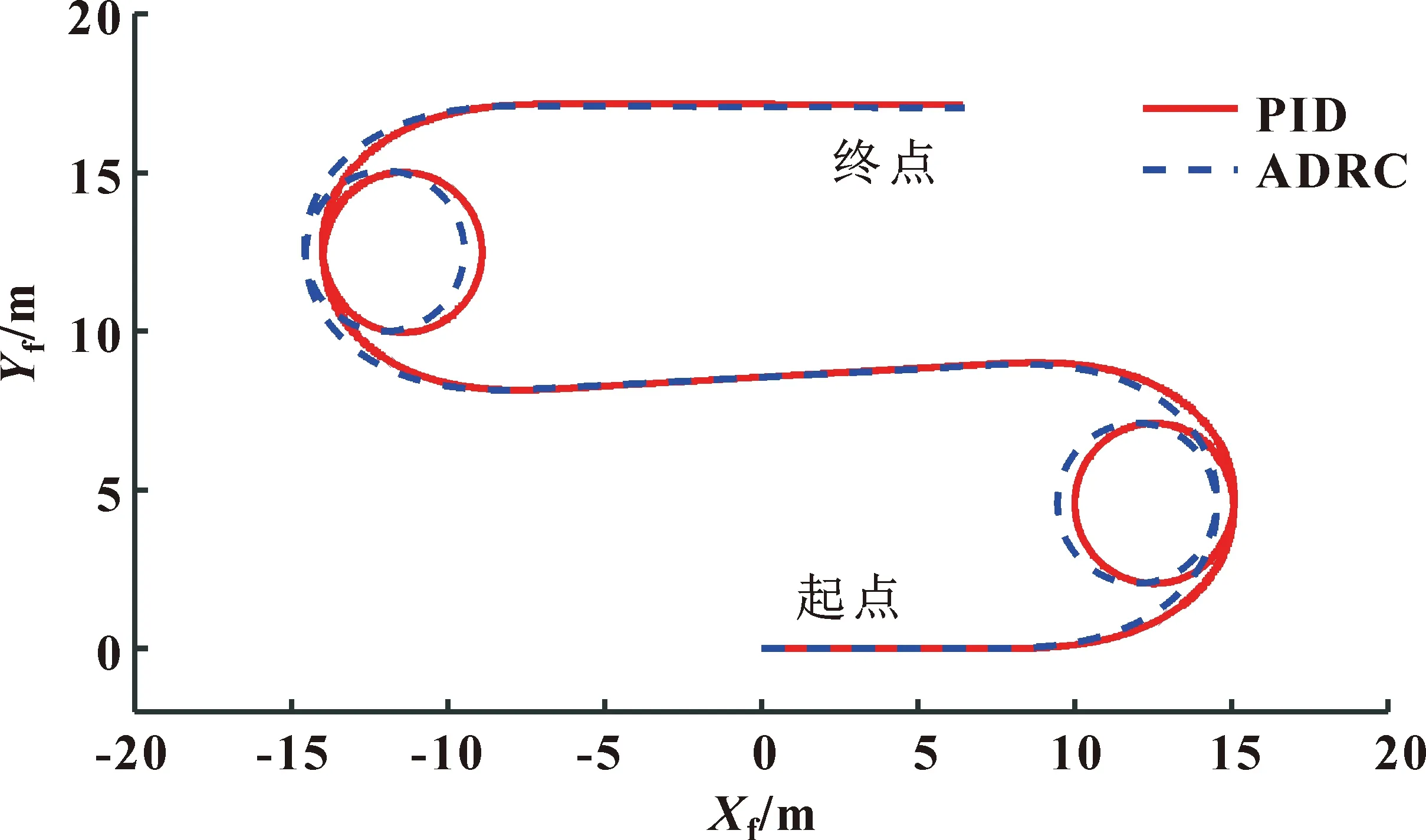
图5 前车体质心运动轨迹
(1)铰接车辆转向运动学分析
仿真过程中,0~5 s内车辆处于摆正位,转向角度为0 rad,此阶段控制车速由0 m/s提升至2.5 m/s左右;5 s后车辆进行转向行驶,最大转向角度为0.8 rad。铰接车辆的运动学状态如图6所示。
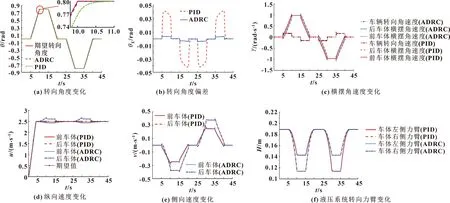
图6 铰接车辆运动学分析
由图6知:5~10 s内铰接车辆转向角度由0 rad转至0.8 rad,转向角速度为0.16 rad/s,与预设转向角速度基本相符,前后车体的横摆角速度数值均逐渐增大,差值在0.14~0.16 rad/s间;为达到预设转向角速度,后车体纵向速度上升,由于驱动力跟踪滞后,前车体纵向速度下降;前车体侧向速度下降,后车体侧向速度先上升后下降;转向系统两侧的转向力臂长度呈逐渐减小趋势,且左侧转向力臂长于右侧,符合铰接车辆前后车体相对转动的特点。10~15 s内车辆的转向角度稳定在0.8 rad,其他状态曲线均保持平稳。15~20 s内车辆转向角度仍以0.16 rad/s回转至0 rad,各状态曲线变化趋势与5~10 s内相反,25~40 s内车辆运动状态与5~20 s内相反。结果表明:相对于PID控制,基于ADRC控制的液压转向系统同样可以满足铰接车辆0.8 rad转向角度需求,车辆转向角度调整更快,转向角度实时跟踪误差更小,控制在0.017 rad以内,当期望转向角度曲率改变后,车辆在0.1 s左右进入稳定行驶状态,转向角度控制精度更高。
(2)铰接车辆转向动力学分析
铰接车辆转向过程中所受作用力主要有转向阻力矩、前后车体侧向力、转向驱动力矩和车体两侧的液压缸压力,各作用力变化趋势如图7所示。

图7 铰接车辆动力学分析
结合图6与图7可知:铰接车辆直线行驶时,转向阻力矩最小,两车体的侧向力和转向驱动力矩在0值附近,液压缸压力差基本稳定,用于抵消转向阻力矩,维持铰接车辆直线行驶状态;转向行驶时,随着转向角度的增加,转向阻力矩逐渐增大,前后车体的侧向力、车辆两侧液压缸的压差均逐渐增大,前车体转向驱动力矩值呈上升趋势,后车体转向驱动力矩与前车体等大反向,相对于PID控制,基于ADRC控制下的车体侧向力、转向驱动力矩和液压缸压力调整速度更快,同时波动也较明显;车辆以最大转向角度稳定转向时,各作用力状态稳定,液压转向系统动力学稳定性好。
3.3 ADRC与PID控制下的转向稳定性对比分析
为研究液压转向系统控制精度对铰接车辆行驶稳定性的影响,以前文所述仿真条件为基础,在第12 s时加入500 N·m转向干扰力矩Tf,然后分别基于ADRC控制器和PID控制器进行铰接车辆转向抗干扰能力仿真分析。转向干扰力矩信号如图8所示,液压转向系统运动学与动力学仿真结果如图9所示。
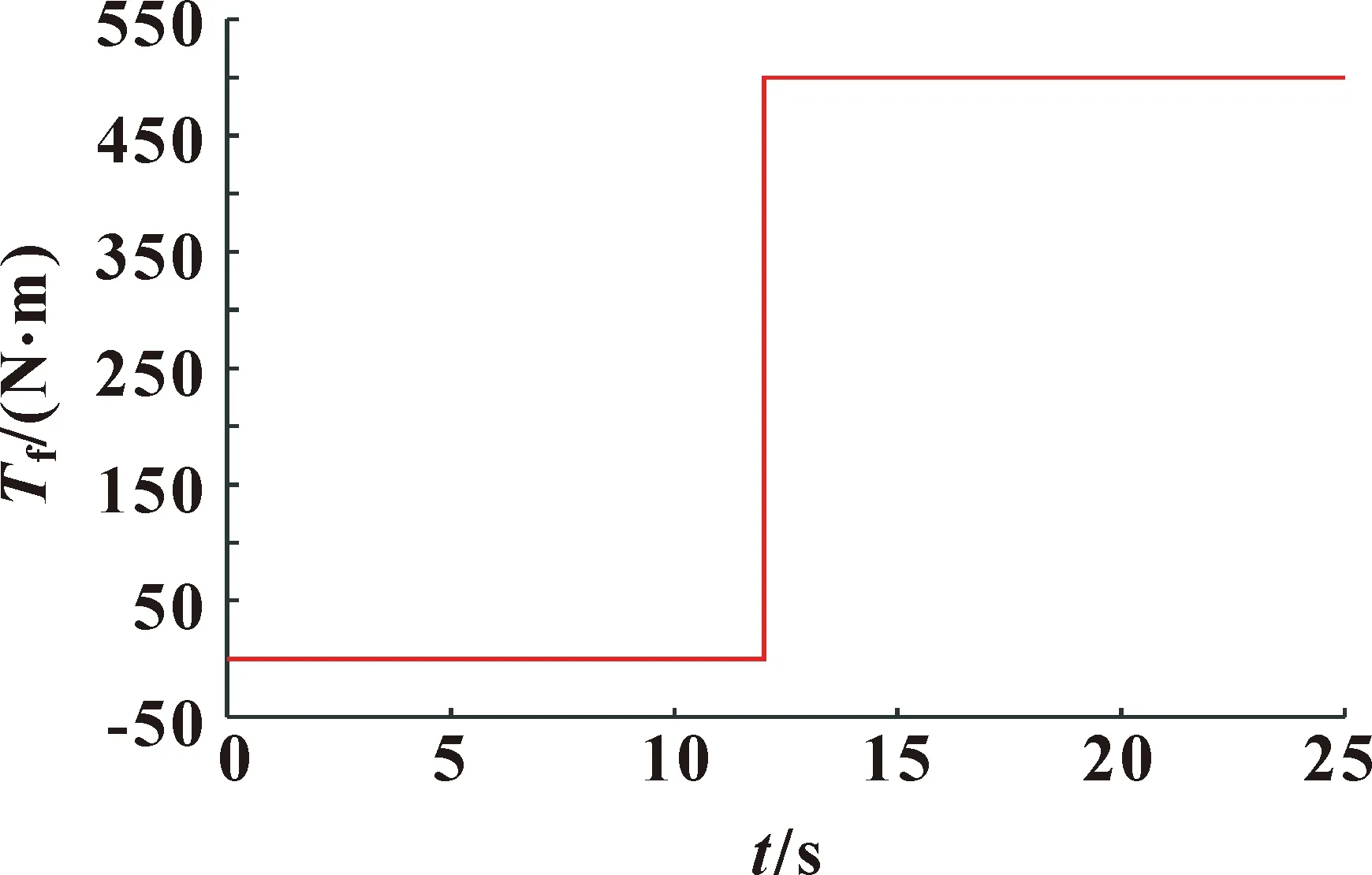
图8 外界干扰力矩变化
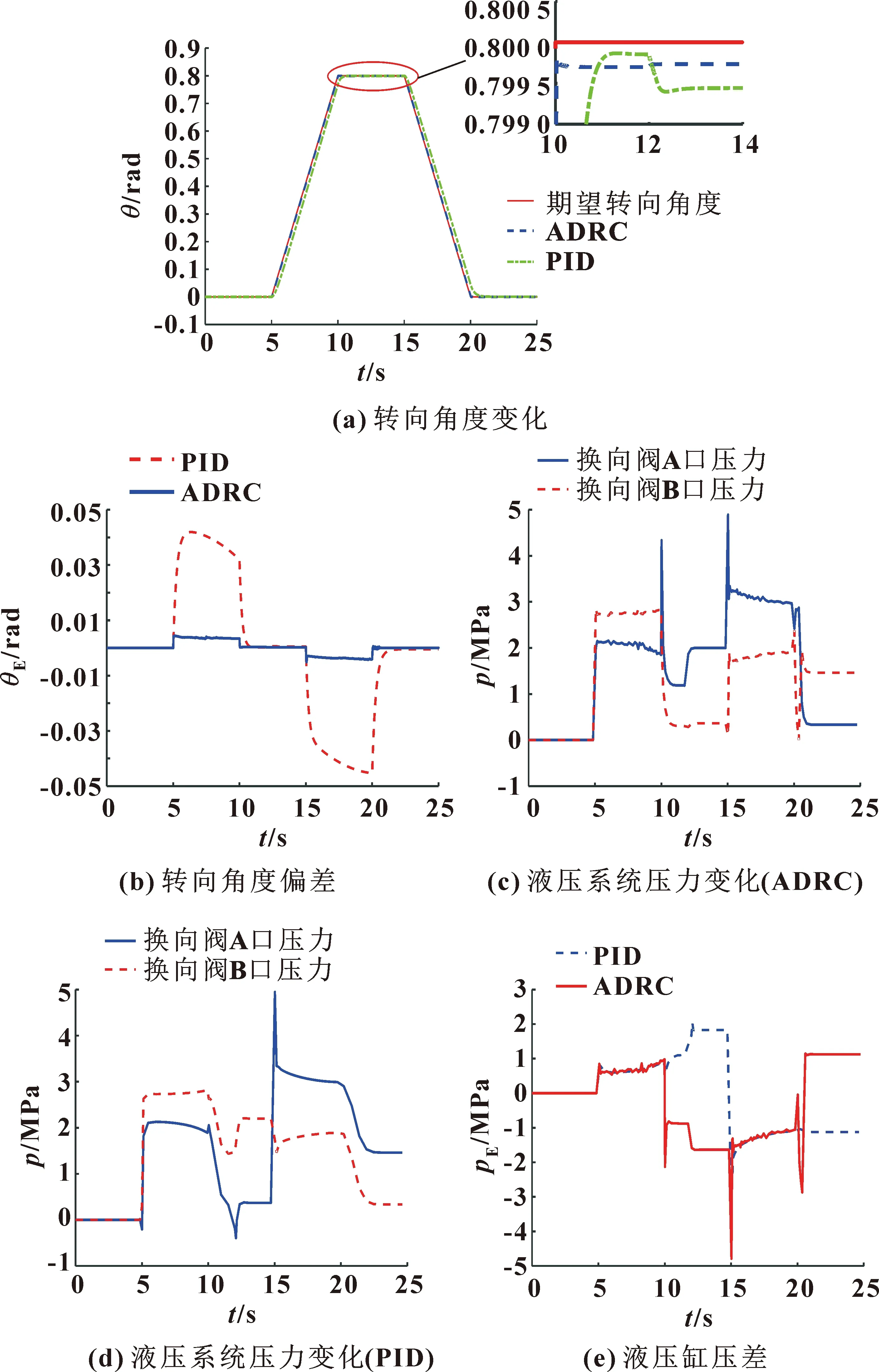
图9 转向控制器性能对比分析
由图9可看出:在5~10 s和15~20 s内,铰接车辆转向角度均处于逐渐变化过程中。液压转向系统在5~10 s受转向阻力矩的作用,在15~20 s同时受转向阻力矩和转向干扰力矩的作用。这两个转向阶段中,基于ADRC控制的转向角度实时跟踪误差小、跟踪速度快。由前文知,12 s时车辆处于以最大转向角度稳定转向过程中,此时加入500 N·m的转向干扰力矩后,为将车辆的实际转向角度快速稳定在目标值,换向阀A口与B口间的压差随之增大,且ADRC控制下的转向角度和液压缸压力以更快的速度趋于稳定。结果表明:相对于PID控制,基于ADRC控制的液压转向系统抗扰动性能更好,可以提高铰接车辆的转向稳定性和路径跟踪精度。
4 结语
根据铰接车辆行驶过程中前后车体的力学特性,结合其运动学特点,基于MATLAB/Simulink建立包括非线性轮胎模型、非线性车身模型、非线性液压转向系统模型和ADRC控制器在内的铰接车辆整车模型,并进行转向运动学和动力学仿真分析。由分析可知,基于ADRC控制的液压转向系统可快速、稳定、无超调地跟踪铰接车辆的期望转向角度,实时转向角度误差在0.017 rad以内,具有更好的抗扰动性能,可提高铰接车辆的转向稳定性和路径跟踪控制精度;同时注意到,液压缸压力在铰接车辆转向角度变化过程中存在波动,且在转向角度曲率改变的瞬间,波动较明显。这两种现象与ADRC控制器参数的整定精度、车轮驱动力分配和液压系统油液弹性模量等因素有关,后续将深入研究。
