工程机械用开关磁阻电机绕组电感计算与分析
2023-11-09冉维斌赵博张存山鲁炳林杨鹏初宇康
冉维斌,赵博,张存山,鲁炳林,杨鹏,初宇康
(1.山东理工大学电气与电子工程学院,山东淄博 255000;2.山东山博电机集团有限公司,山东淄博 255200)
0 前言
随着环境污染与能源枯竭等问题的产生,电传动工程机械逐渐替代内燃式工程机械成为主流[1]。起重机作为升降和移动重物的工程机械,需要循环完成定点取物、起升重物、定点卸载和空载降落,要求频繁起停[2]。现今,驱动源采用异步电机和永磁同步电机,但异步电机长期低速运行下损耗大、效率低;永磁同步电机高温退磁会降低电机使用寿命,且永磁体材料珍贵,制造成本高[3]。开关磁阻电机结构简单、无永磁体、起动转矩高、起动电流小,很好地满足了起重机这类工程机械的需求。
开关磁阻电机独特的双凸极结构,使磁路存在非线性化与局部饱和现象,电磁关系复杂[4]。为描述电感等特性,大多通过有限元仿真来实现[5-7],但在设计初期为满足电机额定性能,需多次调整结构参数,有限元仿真耗时长,无法快速反应,故在设计初期采用磁路解析法[8]确定参数。
UNNEWEHR、KOCH[9]最早提出用线性化方法来描述电机性能;吴建华等[10]进行了定转子极临界重合和半重合位置处的解析计算,提出了附加气隙和动态梯形磁极的方法,降低了计算误差;诸嘉慧等[11]改进了磁参数法,精确了磁导分量计算,得到了误差更小的最小电感解析公式;裴丽娜等[12]用磁路分割法推导出了高速4/2极开关磁阻电机磁化曲线计算式,并通过仿真验证了该计算准确性;王永辉[13]详细推导了传统6/4极开关磁阻电机最小电感与最大电感位置处的磁导,得到了符合样机需要的绕组电感和电磁转矩;ZHANG等[14]推导出了外转子开关磁阻电机在考虑磁饱和与端部电感下相电感的计算式;DAVARPANAH、FAIZ[15]提出了气隙磁导的连续模型,能更简便精确地得到电感与转矩的计算值;VERMA等[16]改进磁通管法得到了最小电感与最大电感位置处气隙磁导的计算式。
本文作者对25 kW三相12/8极开关磁阻电机最小电感与最大电感位置处的磁导分量进行解析计算,得到对应位置处电感的实际值,并通过电感与转子位置角的对应关系,得到了电感的解析曲线,最后进行了仿真验证。
1 基本理论
1.1 数学模型
在忽略铁耗与互感的情况下,开关磁阻电机的数学模型[4]如下所示。
(1)电压平衡方程
U=Ri+E
(1)
式中:U为相电压;R为相电阻;i为相电流;E为反电动势,公式如式(2)所示:
(2)
式中:ψ(i,θ)为相绕组磁链;L(i,θ)为相电感。
(2)机械运动方程
(3)
式中:Te为电磁转矩;J为转动惯量;ωr为转子角速度,公式如式(4)所示;θ为转子位置角;B为摩擦因数;TL为负载转矩。
(4)
(3)机电联系方程
(5)
式中:W′为磁共能,公式如式(6)所示:
(6)
假设忽略磁饱和的影响,式(2)和式(6)可分别化简为式(7)和式(8):
(7)
(8)
联合式(5)和式(8),可求得线性模型下的电磁转矩公式,如式(9)所示:
(9)
电磁转矩与电流的平方、电感变换率成正比,电磁转矩方向与电流方向无关,仅由电感变化率决定。若使电机运行于电动状态,则电磁转矩必须为正,由式(9)可知,电流不为零且dL/dθ>0,即电感上升阶段时电流导通,故电机运行于电动状态。
1.2 电感模型
由上述数学模型可知,电感是描述电机性能的基础,实际开关磁阻电机的电感是关于电流和转子位置角的非线性函数。为突出特性简化计算,对电感进行线性假设,使电感仅与转子位置角有关,令坐标原点θ1=0°,电感公式如式(10)所示:
(10)
(11)
式中:Lmin为最小电感;Lmax为最大电感;θ1为定子励磁极中心线与转子槽中心线重合位置;θ2为定子励磁极与转子极临界重合位置;θ3为定子励磁极与转子极临界完全重合位置;θ4为定子励磁极与转子极临界脱离完全重合位置;θ5为定子励磁极与转子极临界相离位置;θ6为定子励磁极中心线与转子槽中心线经过一个电感周期后再次重合位置。
令开通角为θon,关断角为θoff,则相电感与转子位置角的关系曲线以及相电感与相电流的对应曲线如图1所示。由图1(a)可知:若知晓最小电感、最大电感与转子特殊位置角的实际数值,即可求得相电感的解析曲线。
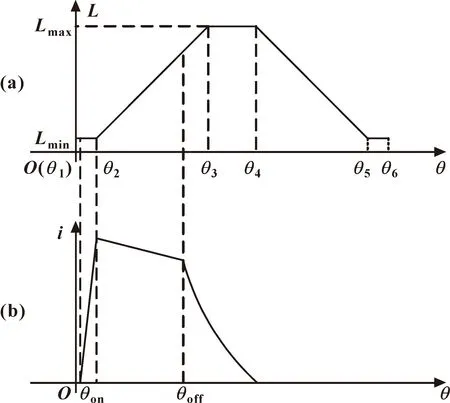
图1 相电感(a)与相电流(b)对应曲线
1.3 电机结构参数
采用三相12/8极开关磁阻电机为研究对象,额定功率为25 kW,额定电压为400 V,额定转速为3 000 r/min,电机结构参数如表1所示。
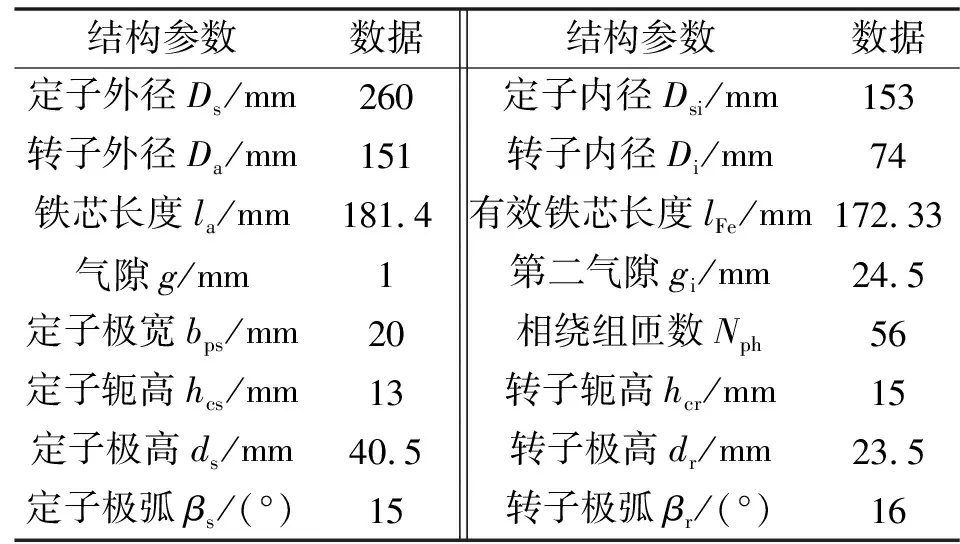
表1 电机结构参数
2 最小电感解析计算
在磁导分量解析计算时,为简化分析,作如下假设[17]:(1)忽略磁饱和与互感,只考虑单相通电情况;(2)忽略端部效应,不计端部电感的影响;(3)假设磁力线由直线和圆弧组成;(4)假设磁极中的磁力线平行于极轴;(5)假设轭中的磁力线为1/4圆弧;(6)假设转轴完全不导磁。
最小电感出现在定子励磁极中心线与转子槽中心线重合位置,磁场关于励磁极呈轴对称分布,由于磁力线在气隙内路径较长,且硅钢片磁导率远大于真空磁导率,故可忽略硅钢片的磁导计算。气隙内的磁力线可分为5种路径,具体分布如图2所示,路径1包含所有的漏磁通,包括从定子励磁极的极边经槽空间到定子轭和定子相邻极的磁通,路径2、3、4、5为主磁通。对各路径的磁导分量分别进行计算。
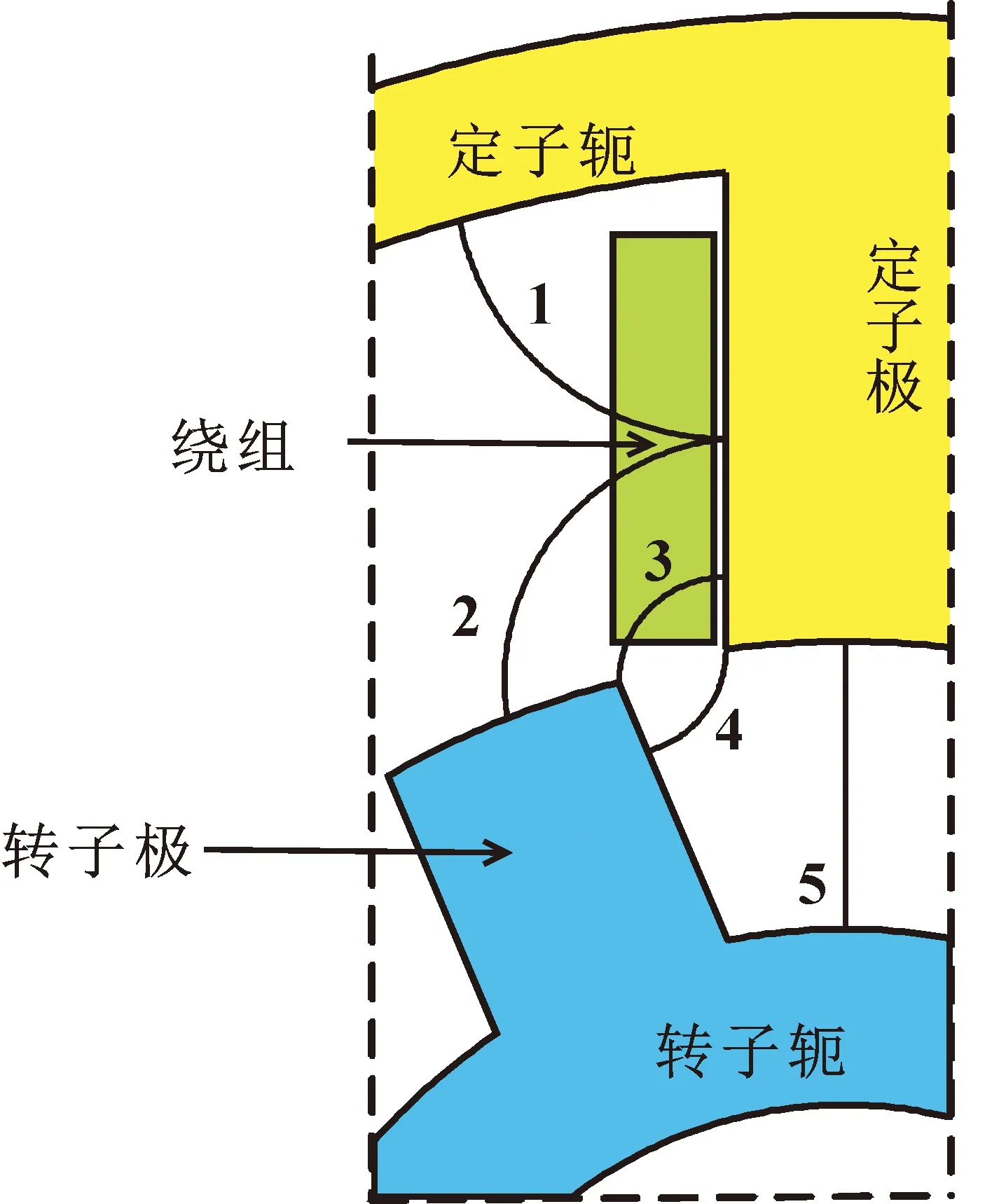
图2 最小电感处等效磁路
每极绕组的磁链为
ψ=2(ψ1+ψ2+ψ3+ψ4+ψ5)
(12)
式中:ψ1、ψ2、ψ3、ψ4、ψ5分别为路径1、2、3、4、5的磁链。
根据图2可求得,相电感为
(13)
式中:Lj为各路径电感;Nph为相绕组匝数;μ0为真空磁导率;Pj为各路径磁导分量。
(14)
2.1 路径1磁导分量计算
图3为路径1的磁路详图,为简化计算用直线段CH替代圆弧CH,假定路径1内充满励磁导体。
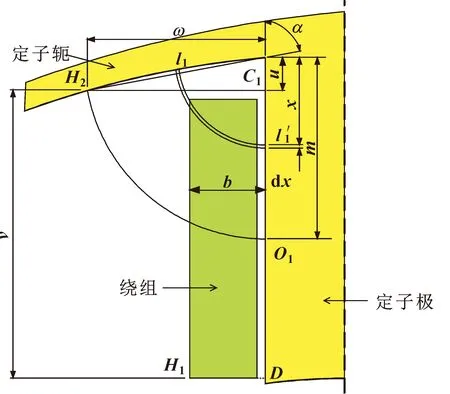
图3 路径1磁路详图
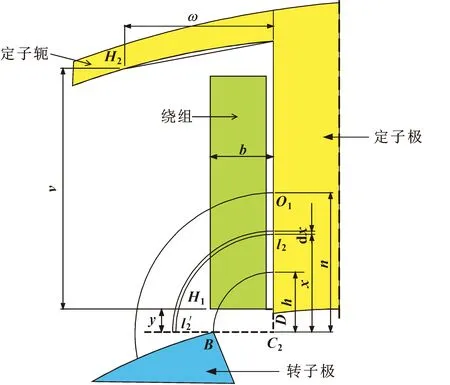
图4 路径2磁路详图
单元磁路l1的长度为
(15)
单元磁路l1的绕组匝数为
(16)
单元磁场强度的通式为
Hx=Nxi/lx
(17)
将式(15)(16)代入式(17)化简得,路径1的单元磁场强度为
(18)
单元磁链的计算通式为
dψx=Nxdφx=NxBxdSx=Nxμ0HxlFedx
(19)
将式(16)和式(18)代入式(19)化简求得,路径1单元磁链的公式为
(20)
将式(20)代入下式可求得路径1的电感为
(21)
将式(21)代入式(14)化简,可求得路径1的磁导分量,如式(22)所示:
(22)
2.2 路径2磁导分量计算
假设路径2是以C2为圆心的同心圆弧,计算步骤与路径1的计算基本一致。
单元磁路l2的长度为
lx=π/2xx∈[h,n]
(23)
单元磁路l2的匝数为
(24)
将式(23)(24)代入式(17)化简可得,单元磁场强度为
(25)
将式(24)(25)代入式(19)可化简求得路径2的单元磁链,如式(26)所示:
(26)
由式(26)可求得路径2的电感,如式(27)所示。根据路径2的电感结合式(14),可求得路径2的磁导分量,如式(28)所示:
(27)
(28)
2.3 路径3磁导分量计算
由图5可知,路径3是由以A、B为圆心的两条圆弧段和垂直于对角线C2C4的直线段组成,其中假设∠ABC2、∠ABA′取值为
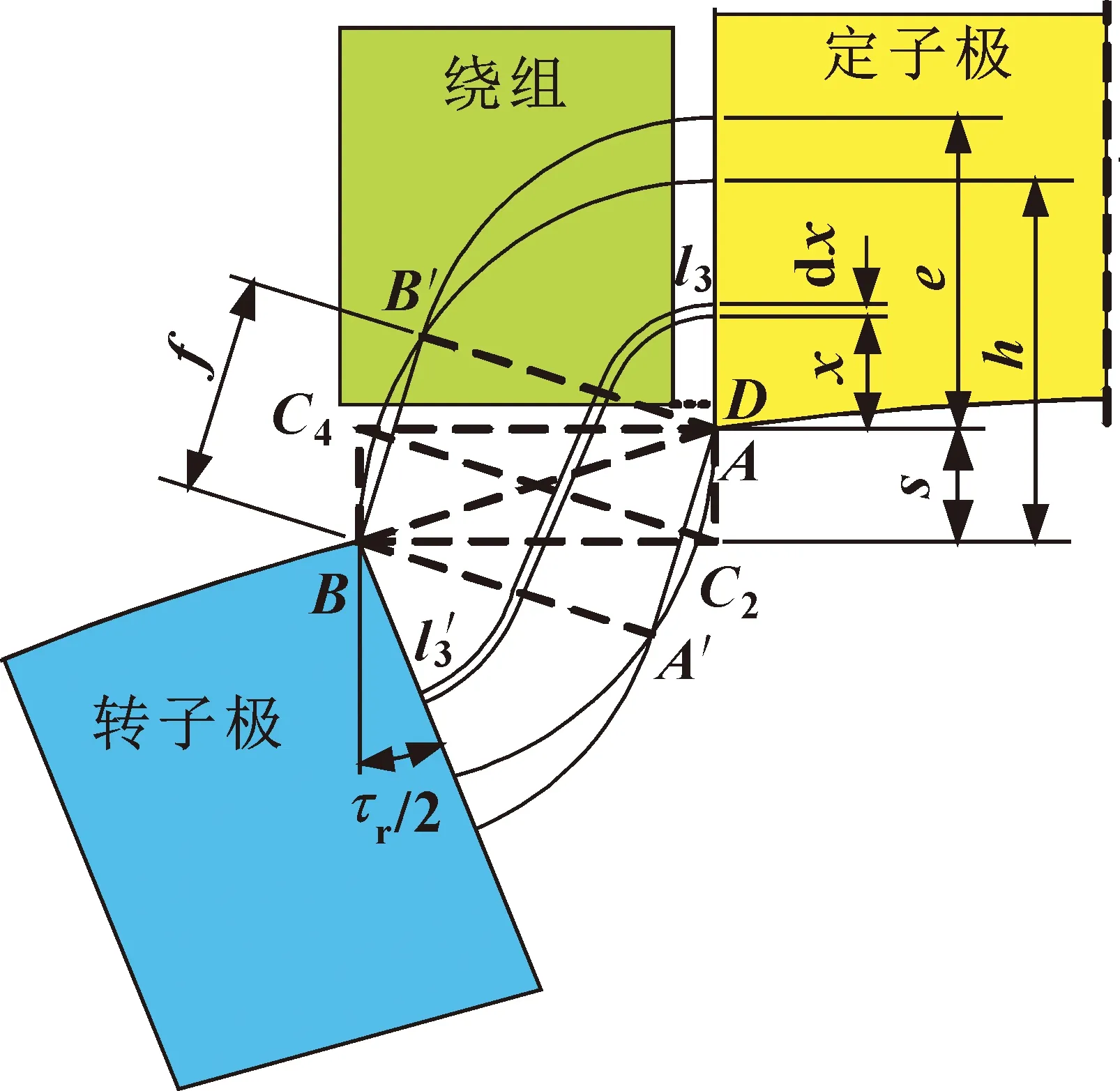
图5 路径3磁路详图
∠ABC2=arctans/h
(29)
∠ABA′=2arctans/h
(30)
故以A、B为圆心的圆弧段半径为
(31)
由图5可知x∈[0,e],单元磁路l3的长度为
(32)
由于磁通路径3所经过的绕组面积比整个绕组面积要小得多,故假定匝数为极绕组匝数。
将式(32)和极绕组匝数代入式(17),结合式(19)可化简求得路径3的单元磁链为
(33)
由式(33)可得,路径3的电感计算式为
(34)
将式(34)代入式(14)化简求得,路径3的磁导分量为
P3=
(35)
2.4 路径4磁导分量计算
路径4的磁路详图如图6所示,图中磁通路径是以C4为圆心的同心圆弧,匝数为极绕组匝数。
结合图5和图6可得,扇形角∠OrC4O2为
∠OrC4O2=arctan(h/s)
(36)
令图6中路径4与路径5的分界条件满足式(37)的要求:
(βr/2+arctan(h/s))t=gi
(37)
由式(37)可得:
(38)
单元磁路l4的长度为
lx=xarctan(h/s)x∈[h,t]
(39)
将式(39)分别代入式(17)和式(19)可求得,路径4的单元磁链为
(40)
由式(40)可得,路径4的电感计算式为
(41)
将式(38)和式(41)代入式(14)化简可得,路径4的磁导分量为
(42)
2.5 路径5磁导分量计算
路径5的磁路详图如图6所示,路径5磁路由一组平行直线组成,匝数为极绕组匝数。
单元磁路l5的长度为
lx=gi
(43)
在图6中可见,路径5所占区域的宽度已知,故可直接求取路径5的电感为
(44)
将式(38)和式(44)代入式(14)化简可得,路径5的磁导分量为
(45)
2.6 最小电感值的求解
通过表1电机结构参数,经测量可得图3—图6中参数的具体数值,如表2所示。
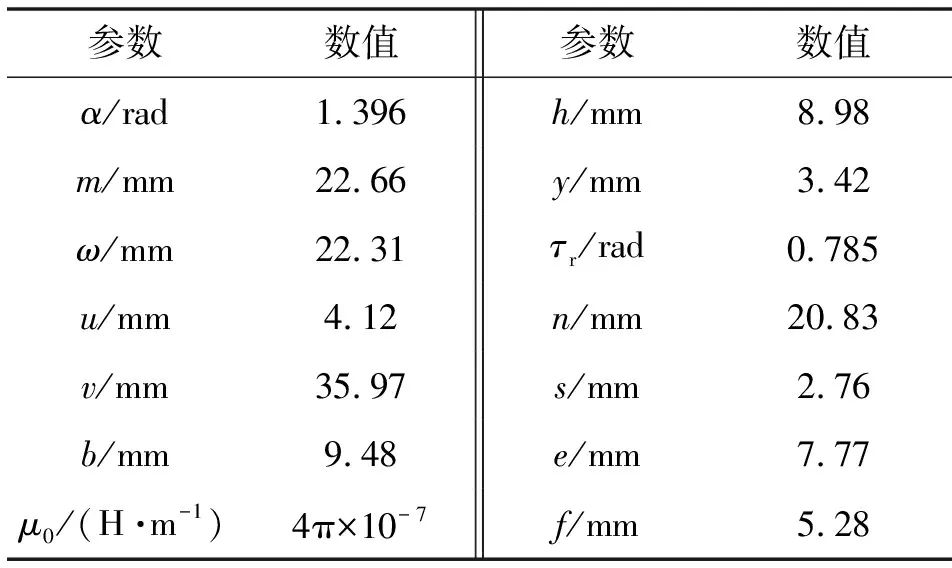
表2 磁导分量计算中各参数的数值
将表2中数据分别代入式(22)(28)(35)(42)(45)可求得各路径磁导分量的值,如表3所示。

表3 磁导分量数值
将计算的各路径磁导分量代入式(13)可求得相电感的最小值为Lmin1=0.531 mH。
由文献[8]可知,端部电感占总电感的比重会随着对齐程度的增大而减小,最小电感位置处的端部电感占总电感的比重大。在上述磁导分量解析计算中忽略了端部电感的影响,因此计算所得的电感偏小,造成较大的计算误差,故用一种等效方法将端部电感计算在内,以此缩小计算误差。
进行等效气隙处理,使其值等于各路径磁路长度的平均值。
(46)
在考虑端部磁场情况下,有效铁芯长度为
le=la+2n(1-σ)
(47)
式中:σ为卡特系数,计算公式如式(48)所示:
(48)
由上述各式可求得考虑端部磁场情况下最小电感为
Lmin=Lmin1(2le/la-1)
(49)
将表1和表2的数据分别代入式(46)—(49)可求得,考虑端部磁场情况下的最小电感值为Lmin=0.667 mH。
3 最大电感解析计算
最大电感出现在定子励磁极与转子极完全重合位置。该磁通路径为短磁路,且由于磁路的对称性,取1/4电机模型的磁路详图进行解析说明。如图7所示,磁力线经定子极、气隙、转子极、转子轭和定子轭形成闭合回路,图中、分别代表电流流入和电流流出,为方便计算假定磁通在磁路中均匀分布且无漏磁。
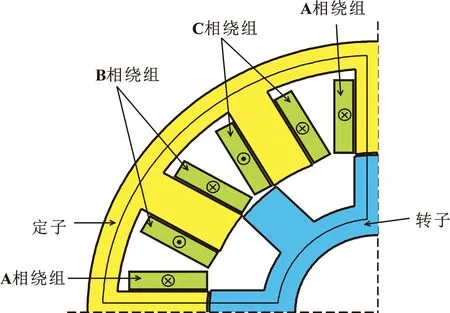
图7 最大电感处磁路详图
定子轭导磁路径长度及导磁截面积为
(50)
Scs=hcslFe
(51)
定子极导磁路径长度及导磁截面积为
lps=2ds
(52)
Sps=1/2bpslFe
(53)
转子极导磁路径长度及导磁截面积为
lpr=2dr
(54)
Spr=1/2bprlFe
(55)
转子轭导磁路径长度及导磁截面积为
lcr=π/4(Di+hcr)
(56)
Scr=hcrlFe
(57)
铁芯的磁导计算式为
Λ=μS/l
(58)
式中:l为铁芯各部分导磁路径长度;μ为铁芯磁导率;S为铁芯各部分导磁截面积。
铁芯处的总电感计算式为
(59)
假定铁芯各部分磁导率均等于μ,将式(50)—(57)代入式(58)求和可得,该磁路下的铁芯总磁导为
(60)
将式(60)代入式(59)可求得,铁芯处的总电感为
(61)
气隙导磁路径长度及导磁截面积为
lg=g
(62)
(63)
由式(62)和式(63)可得,气隙总电感为
(64)
结合上述各式可求得,最大电感为
Lmax=Lcore+Lg=
(65)
该电机采用的硅钢片型号为DW310-35,B-H曲线如图8所示。
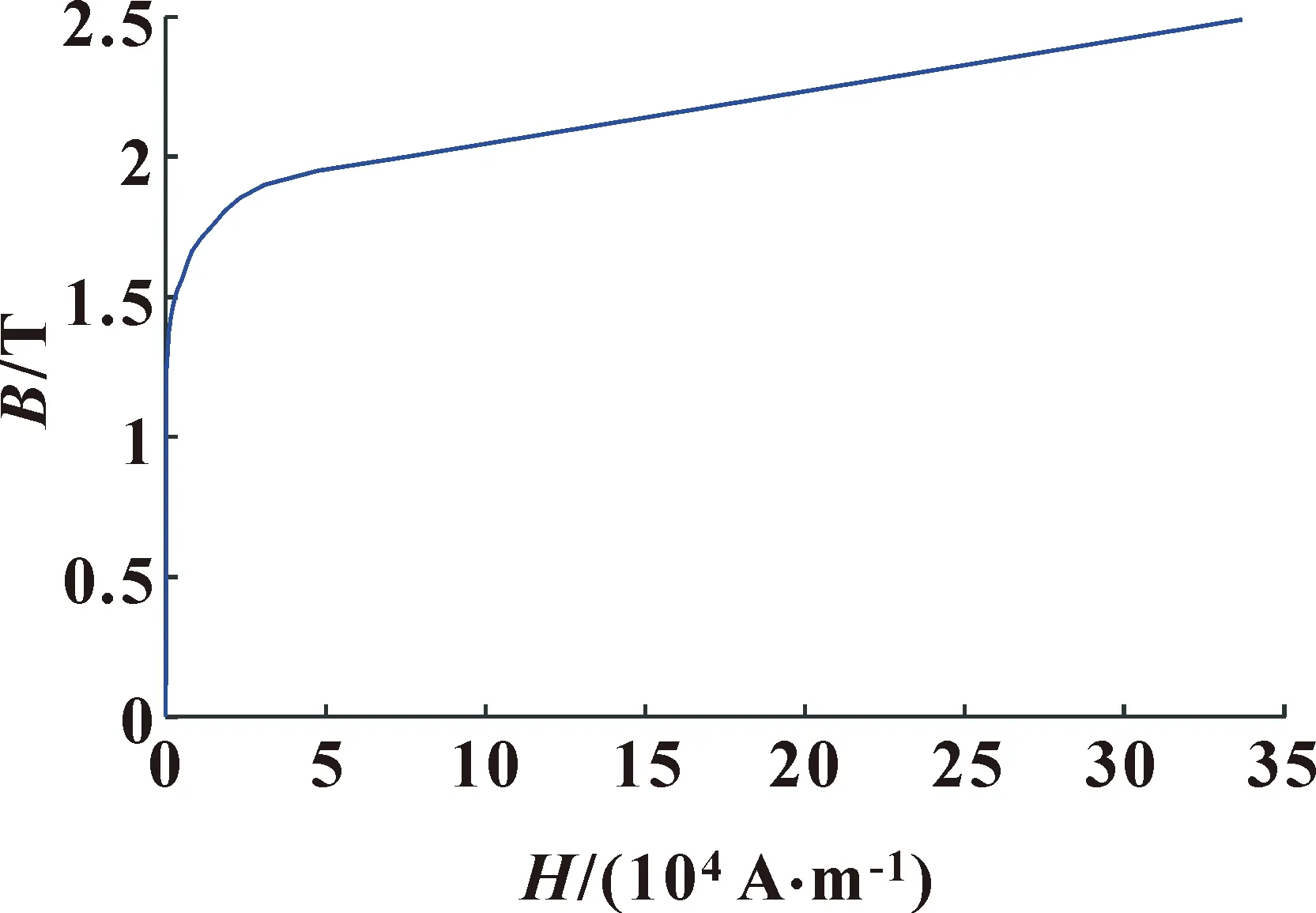
图8 B-H曲线
由图8可知,铁芯磁导率近似取μ=8.53 mH/m,根据表1的数据结合式(61)可求得,最大电感值为Lmax=3.856 mH。
在最大电感位置处,定转子处于完全重合状态,端部电感对总电感的影响要小得多,故在最大电感位置处忽略端部电感的计算。
4 电感曲线解析与仿真验证
4.1 电感曲线解析
根据上述解析计算已求得相电感的最小值和最大值,由式(10)和式(11)可知,只需知晓特殊位置处的转子位置角,即可求得实际的相电感解析曲线。
定子励磁极与转子极临界重合位置θ2为
(66)
式中:Nr为转子极数。
定子励磁极与转子极临界完全重合位置θ3为
(67)
定子励磁极与转子极临界脱离完全重合位置θ4为
(68)
定子励磁极与转子极临界相离位置θ5为
(69)
定子励磁极中心线与转子槽中心线再次重合位置θ6为
(70)
将各特殊位置计算所得的转子位置角、最小电感值和最大电感值代入式(10)可得
(71)
由式(71)可得到电感的解析曲线,如图9所示。
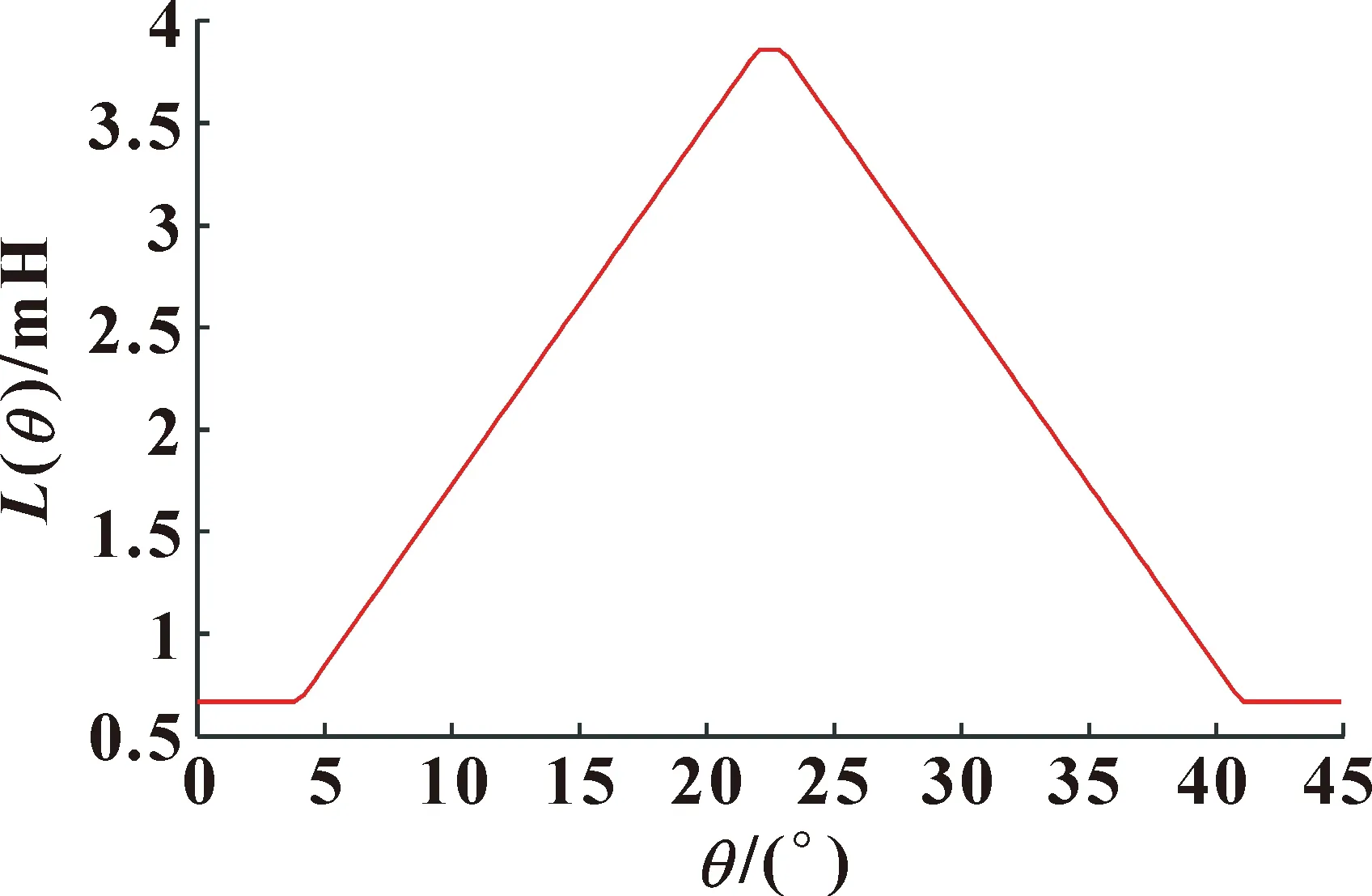
图9 相电感解析曲线
4.2 仿真验证
为避免因仿真设计造成不必要的误差,在仿真时忽略涡流效应,电机采用单相通电。图10为电机最小电感位置和最大电感位置处的磁密云图,由于采用单相通电,电机磁密小,不易出现饱和现象。
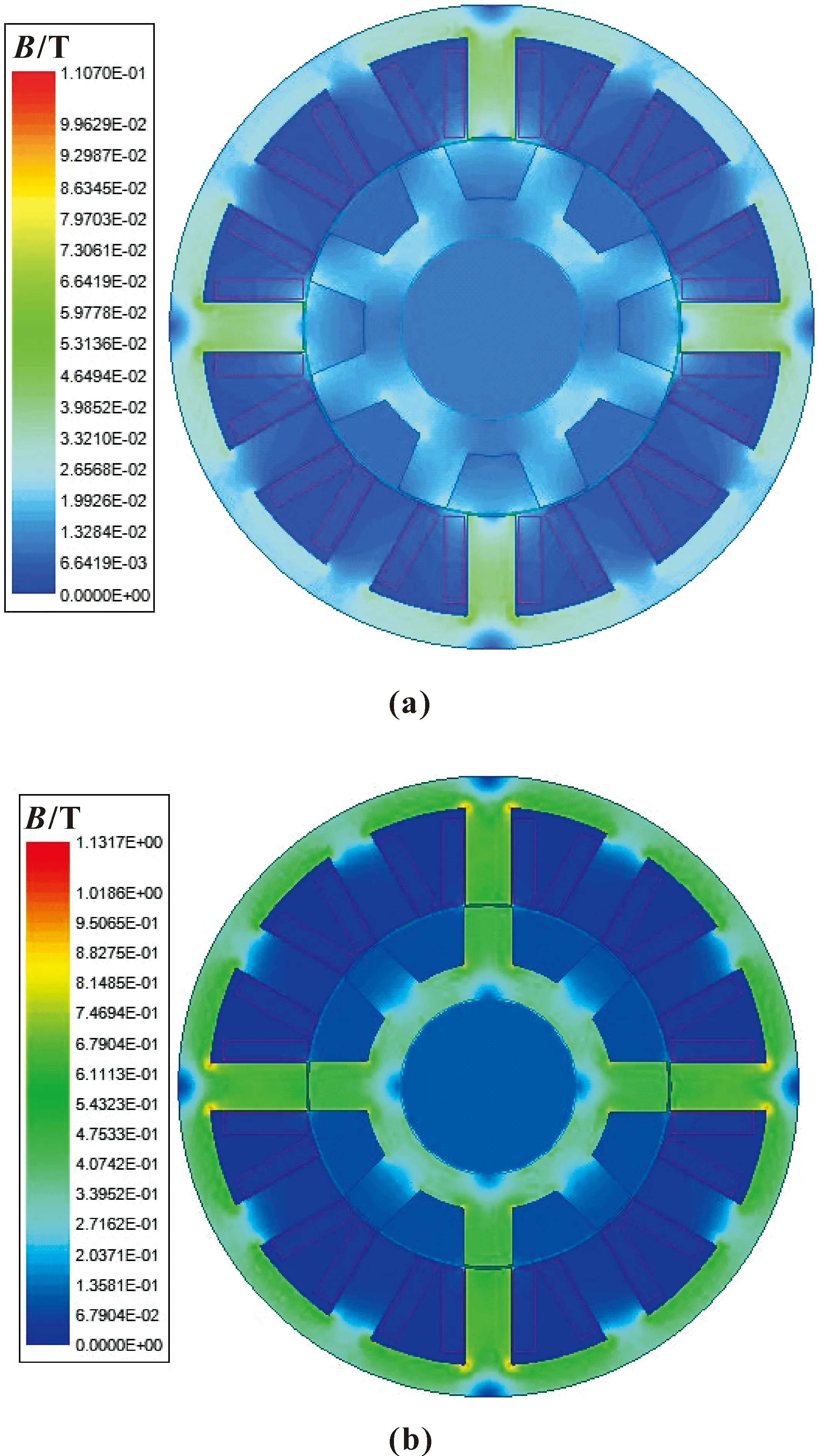
图10 最小(a)、最大(b)电感位置磁密云图
图11为电机最小电感位置和最大电感位置处的磁力线图,由此可见解析计算中磁通路径精确度极高,其中在解析计算中将图11(a)中定子励磁极到定子轭的磁力线和定子励磁极到定子相邻极的磁力线集合在一起共同组成磁通路径1,其他路径均与仿真结果相符。
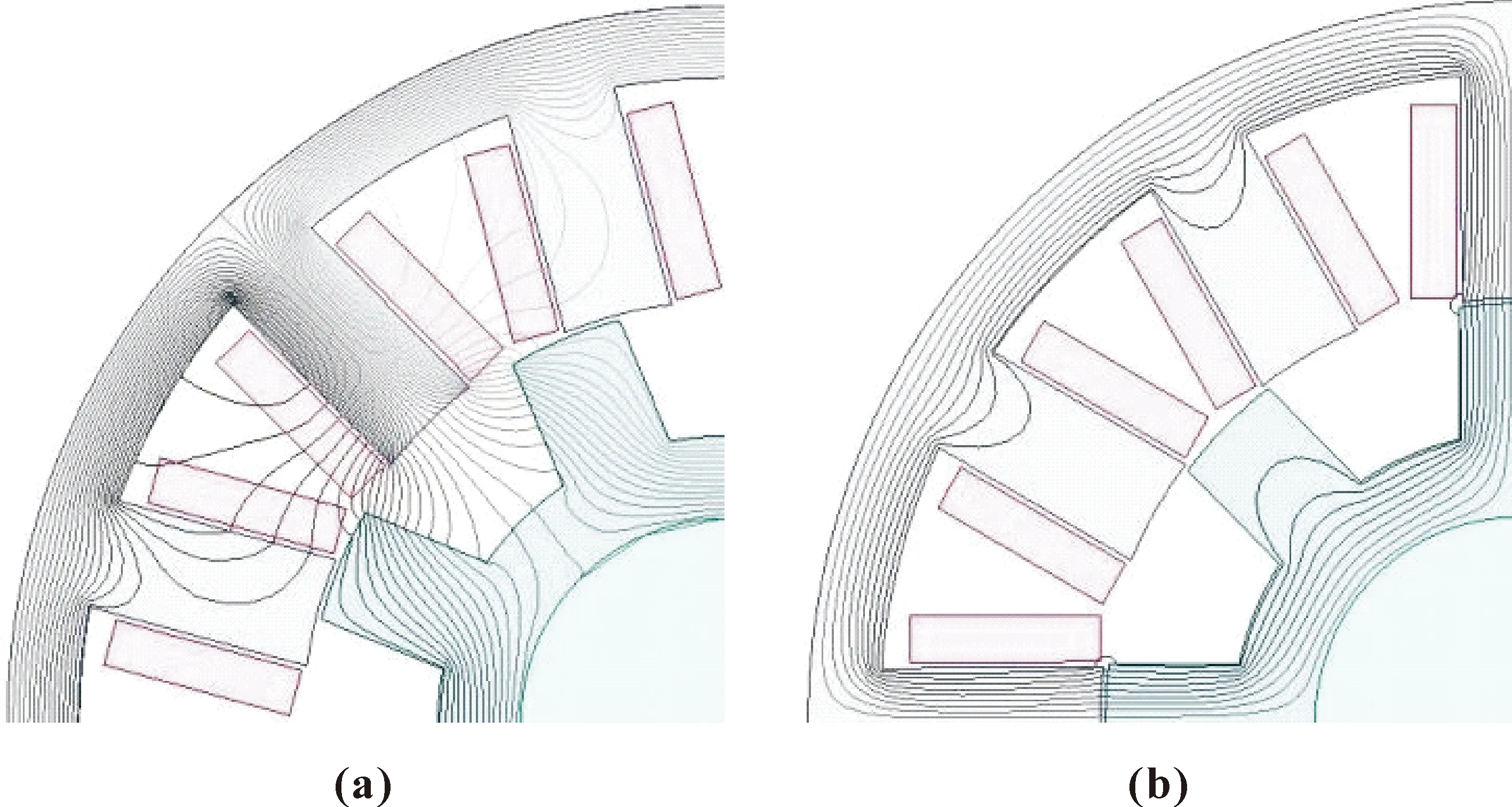
图11 最小(a)、最大(b)电感位置磁力线图
将有限元仿真得到的电机相电感曲线与相电感的解析计算曲线进行比较,如图12所示:在定转子极边临界重合位置处误差较大。这是由于在解析计算时忽略了该处磁场局部饱和的影响,另外该电机转子为平行齿结构,在定转子极的极边重合过程中,与梯形齿维持在最小电感值不变的情况有所不同,平行齿会根据极边重合度的增大而使电感略有提高,故会使临界重合位置处误差偏大。
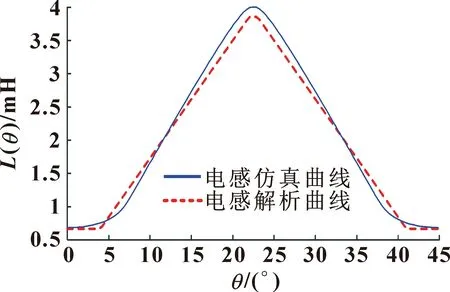
图12 两种计算方法下相电感比较
本文作者主要对最小电感和最大电感位置处进行解析计算,由图12可知,这两种特殊位置处电感的相对误差较小,相对误差计算值如表4所示,误差均在4%以内,基本满足电机设计与优化的要求。
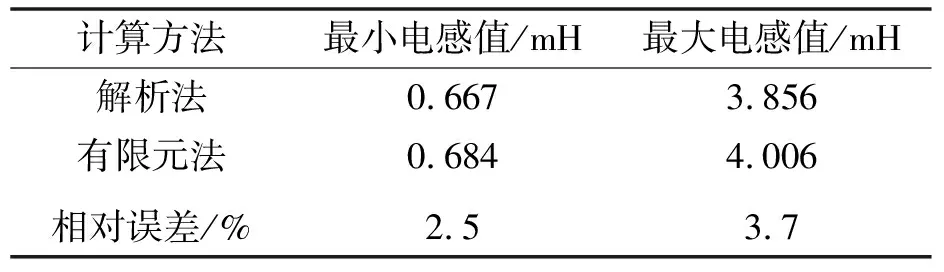
表4 不同方法下电感值的比较
取开通角为0°、关断角为14.5°,由电感可得到磁链的解析曲线,与磁链仿真曲线进行对比。如图13所示:顶点误差为5.1%,且误差最大在10%以内。两种曲线近似吻合,进一步证明了该解析法的准确性。
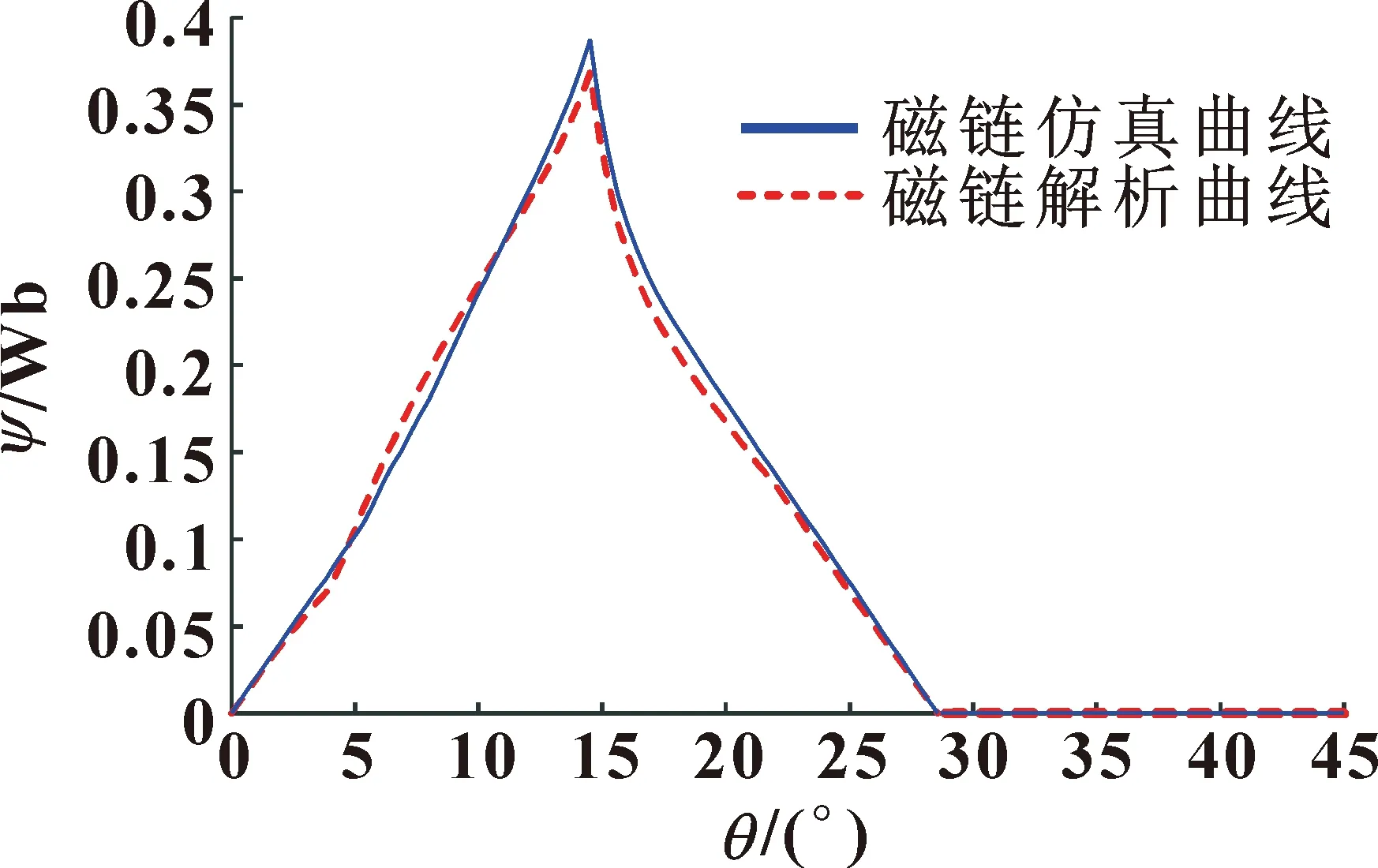
图13 磁链解析曲线与仿真曲线的比较
5 结论
围绕三相12/8极平行齿结构开关磁阻电机展开,以工程机械用开关磁阻电机为实例,通过对磁导分量的解析计算,得到了电机的电感特性,由此得出以下结论:
(1)得到了12/8极开关磁阻电机解析计算的磁路详图,并通过仿真验证了该磁路的准确性;
(2)通过对最小电感与最大电感位置处的磁通路径进行解析,推导出了该电机各磁通路径的磁导分量解析式;
(3)由磁通分量解析式,求得了最小电感与最大电感,并推导出了符合该电机的转子特殊位置角公式,得到了相电感与转子位置角的解析曲线;
(4)通过仿真验证,电感相对误差在4%以内,磁链相对误差在10%以内,证明了该方法具有较高的精确度,达到了预期的设计要求,为电机的初步设计与后期优化提供了理论依据和参考。
