基于机器视觉的曲轴圆度误差评定
2023-11-09李长安张丹隋文涛逯海滨窦亚萍
李长安,张丹,隋文涛,逯海滨,窦亚萍
(1.山东理工大学机械工程学院,山东淄博 255000;2.山东理工大学电气与电子工程学院,山东淄博 255000)
0 前言
曲轴对于保障发动机正常可靠运行意义重大,圆形特征是曲轴最基本的几何元素之一,因此对曲轴进行圆度误差检测至关重要。机器视觉有着高效、非接触、高精度等特点,在测量领域中有着广阔的发展前景[1-2]。前人已做诸多研究:文献[3]在接触式曲轴轴颈同步测量方法的基础上,利用多传感器修正轮廓,测量精度显著提高;文献[4]利用机器视觉系统对各种形状几何公差进行检测但检测精度较低;文献[5]对钢领内圈圆度视觉检测方法进行了研究,采用最小二乘法得到亚像素边缘的理想圆心,但并不符合最优的评定准则。
本文作者使用高分辨率工业相机代替传统检测工具,并利用数字图像重构曲轴截面圆周的离散点模拟接触式测量方式,规避了最优法的收敛问题和大量迭代的计算误差,可以有效准确地计算曲轴圆度误差。
1 圆度视觉评定系统
1.1 硬件组成
文中圆度视觉评定系统实验台如图1所示,由夹紧、滑动和旋转机构以及电机、编码器、背光光源、CMOS相机和计算机组成。三爪卡盘、相机移动台作为动态部件由步进电机驱动,用于控制曲轴的旋转运动和相机的水平、垂直方向运动,并通过电机与编码器耦合控制电机的转速。
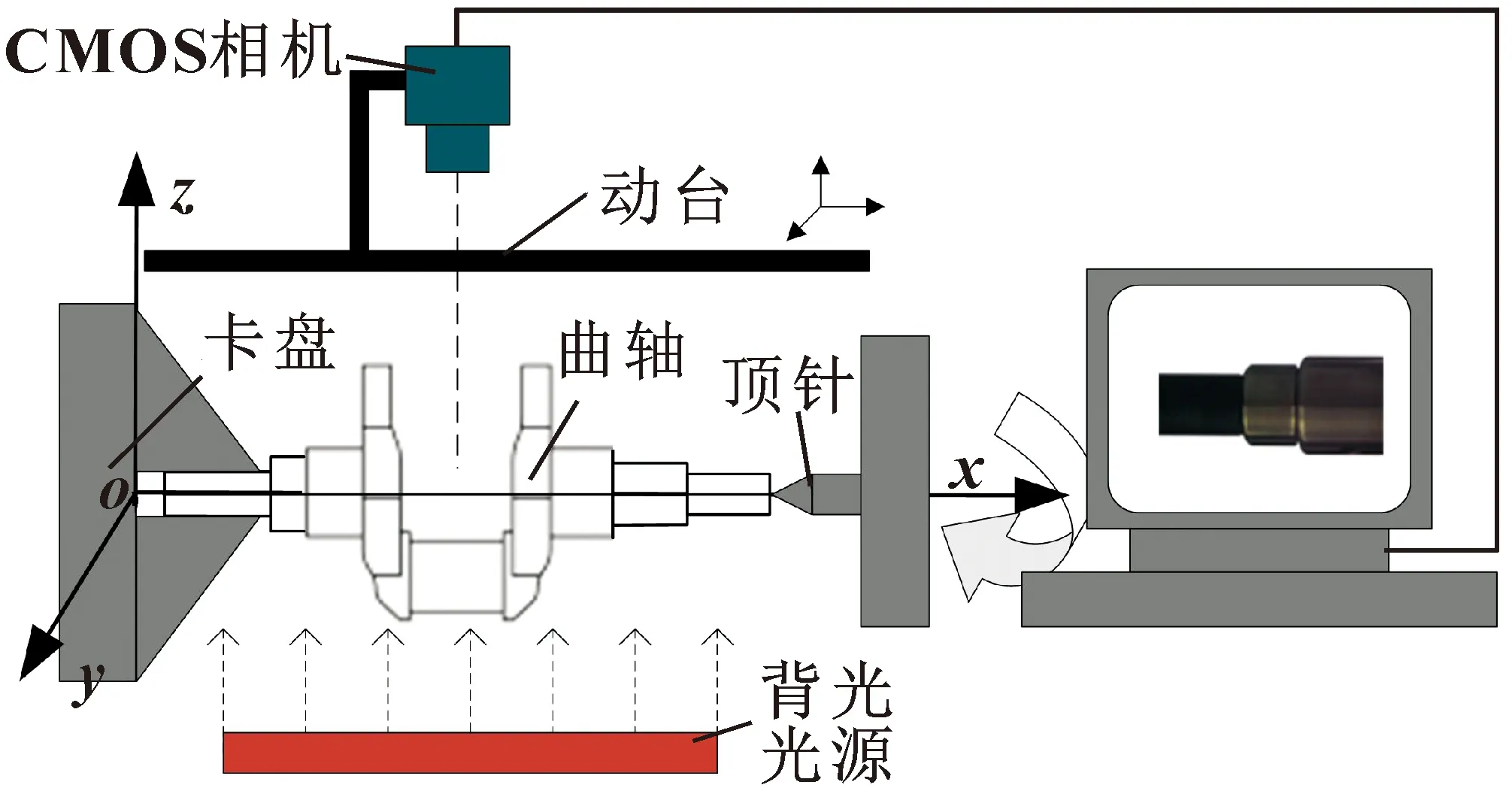
图1 圆度视觉评定系统实验台
1.2 图像处理算法
1.2.1 畸变校正与像素当量计算
为了提高检测精度,需进行相机标定,其具体流程如图2所示。
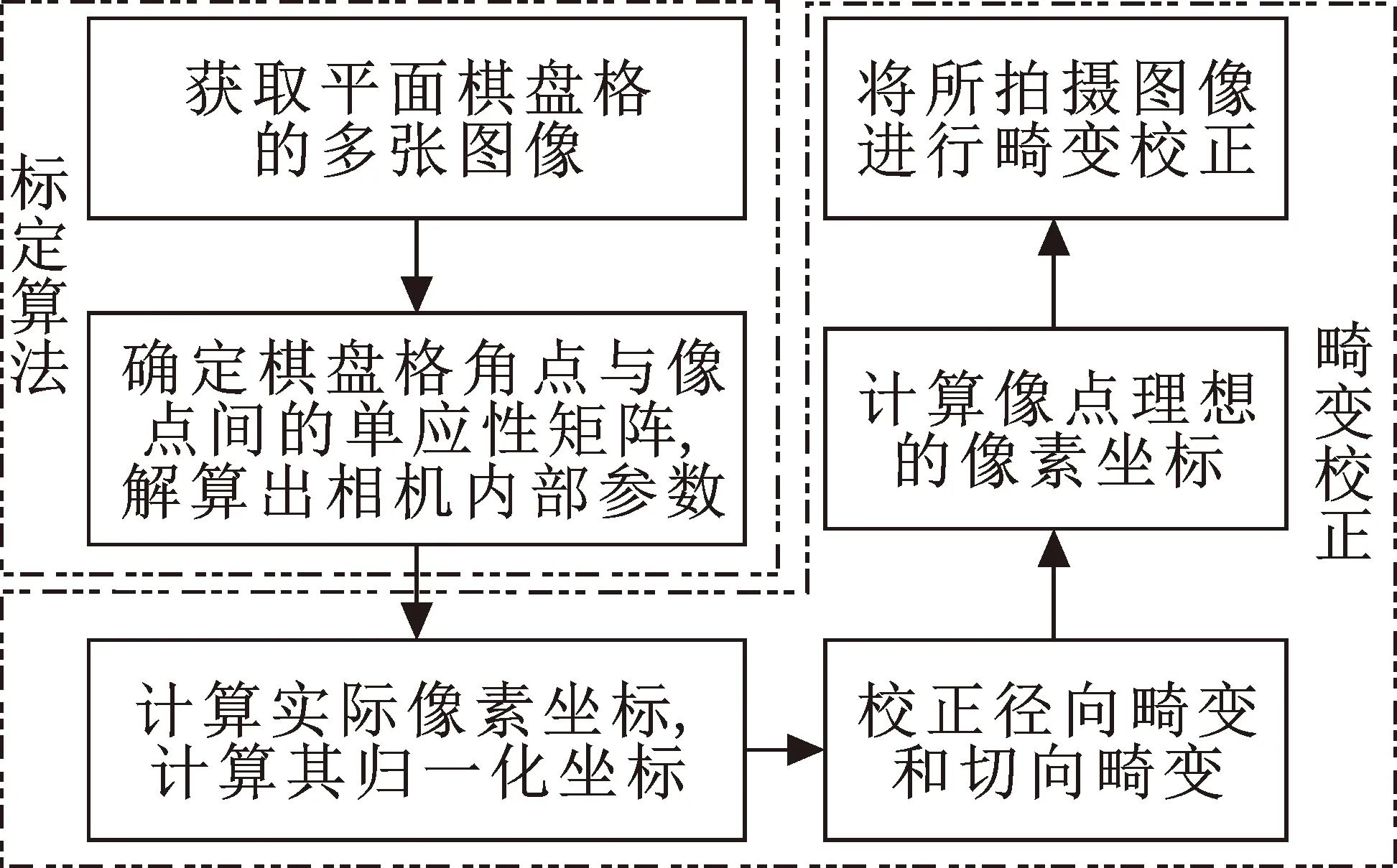
图2 畸变校正流程
在畸变校正过程中,引入Heikkila模型[6],由于系统畸变不大,取泰勒级数展开式前3项,主要公式如下所示:
(1)
式中:k1、k2为径向畸变系数;p1、p2为切向畸变系数;(u0,v0),(u,v)分别为无畸变像点和实际像点坐标。
1.2.2 图像预处理
综上所述,新媒体时代档案文化价值的发掘与传播有着重要的实际作用,而在新媒体时代下对于档案文化的挖掘要根据群众的不同需求进行档案文化挖掘、利用新媒体技术挖掘声像档案文化。另外,在新媒体时代下对档案文化进行传播时要增强档案文化传播意识,激发档案文化影响、大力发展档案文化产业和产品、有效利用新媒体,创新档案文化传播方式,进而有效地对档案文化进行传播。
在计算机获取待测图像后划定感兴趣区域(Region of Interest,ROI)以减少图像数据量,随后对ROI图像进行预处理。采用改进的形态学自适应滤波方法对图像去噪,自适应阈值分割法获得二值图像,Canny算法进行整像素边缘提取,如图3所示。

图3 图像处理
1.2.3 亚像素检测算法
工件的真实边缘并非占满整个像素,需要精确到浮点坐标位置。为达到精密检测的要求,需进行亚像素检测[7]。
首先利用梯度函数(2)获得像素点梯度值,然后代入插值公式(3):
(2)
(3)
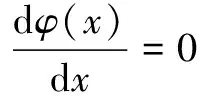
(4)
所得x值代入式(2)获得对应梯度函数,再代入下式:
Xi=x+
(5)
求得x方向的亚像素坐标Xi,同理可求得亚像素坐标Yi。最后对亚像素点(Xi,Yi)进行多项式拟合,如下式所示:
Lm(x)=a0+a1x+a2x2+…+amxm
(6)
亚像素级边缘提取效果如图4所示,可精确到约0.2个像素。
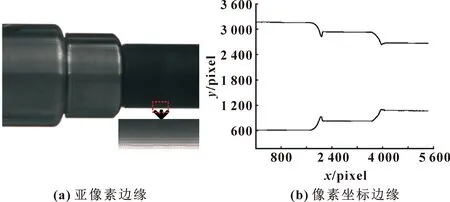
图4 亚像素检测
1.3 倾斜校正
设备的装配误差会导致图像倾斜,从而增大图像边缘位置误差。为了提高检测精度,利用Hough变换[8]对采集图像进行倾斜校正。
首先需要得到经亚像素处理后图像的轴线,如图5所示,在上边缘取点(xi,yi),对应的下边缘点(xj,yj)到其距离应最小,则其对应轴线的坐标为(x,y),如下式所示:
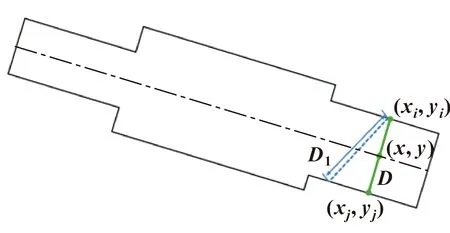
图5 轴线获取示意
(7)
(8)
计算理想轴线倾斜角度,通过旋转补偿倾斜角从而达到校正目的。校正结果如图6所示,实线为水平线,虚线为理想轴线。

图6 倾斜校正
2 圆度评定
2.1 三维重构
圆度评定只需确定截面轮廓信息,文中基于单目视觉进行了确定x坐标的三维重构[9]。
曲轴与相机的位置关系如图7(a)所示,在像素平面中上下边缘点坐标为(yi,zi),利用旋转角度重构关联点。
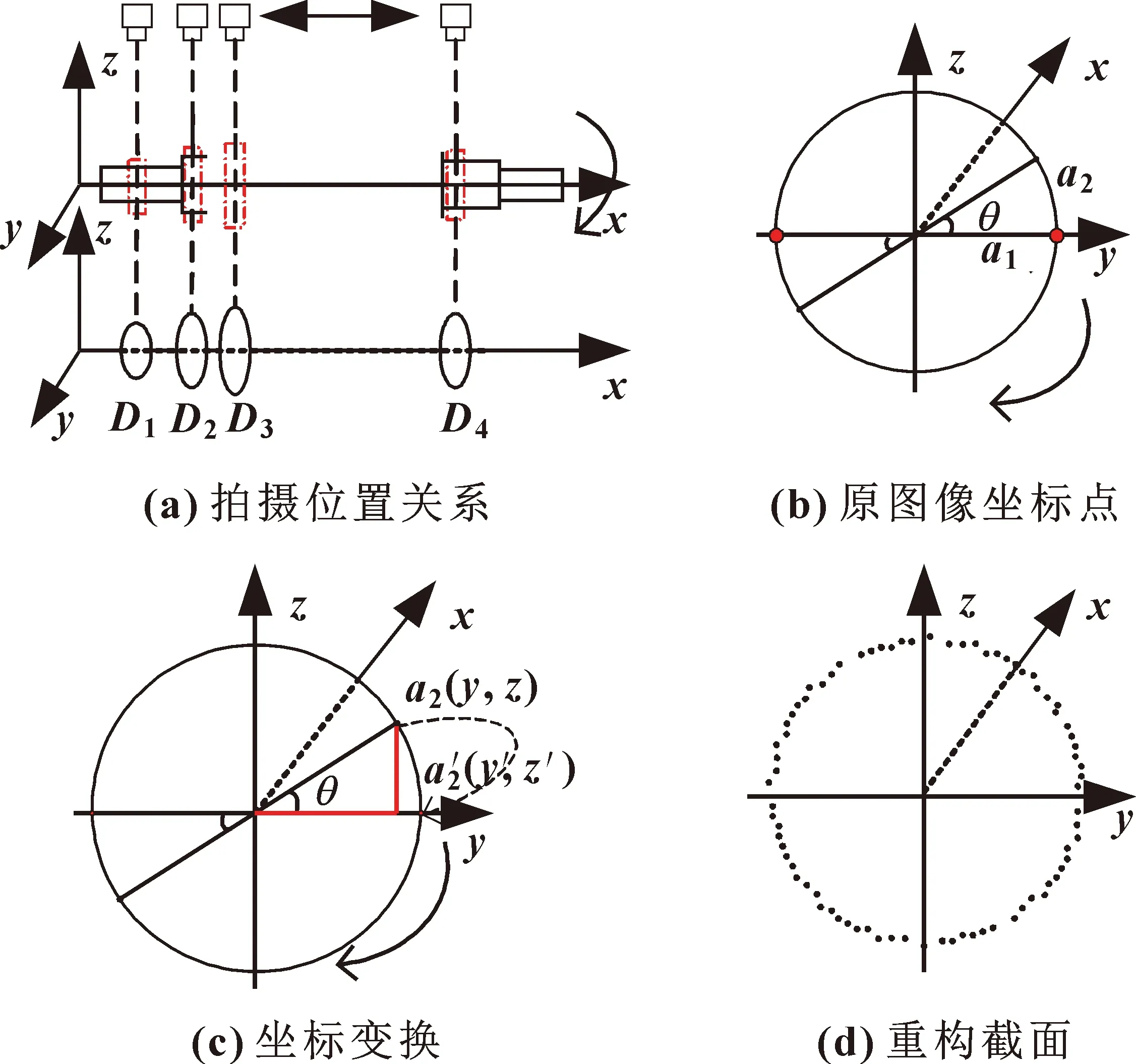
图7 三维重构
图7(b)中a1坐标为(x0,yi,0),相对y轴方向180°点的坐标为(x0,-yi,0),单次旋转角度为θ。旋转后获取当前视角下二维图像,原a2(x0,y2,z2)转到a′2(x0,y′2,z′2),如图7(c)所示,旋转180°后可测得完整圆周,如图7(d)所示。计算重构后的坐标:
yi=y′icos((i-1)θ) (i=0,1,…,180/θ)
zi=z′isin((i-1)θ) (i=0,1,…,180/θ)
(9)
式中:(yi,zi)为实际位置;i为旋转次数;θ为单次旋转角度。
2.2 圆度评定模型
提出一种通过建立曲轴直径与圆度之间的关系来测量曲轴主轴圆度误差的方法,符合最小区域评定准则。确定一对半径差值最小的同心圆C1和C2,使测量点包含在同心圆之间,其中R1和R2分别为C1和C2的半径,中心点位于一点(xc,yc)。
其数学模型可表示为
(10)
具体操作步骤:由第1.3节可得曲轴旋转中心轴线坐标,其到x轴的距离为Yc,从中心轴到图像的上、下两侧的距离分别表示为Yup和Ydown,如图8所示。按固定角增量旋转拍摄,可得不同角度Yup和Ydown,经三维重构复现截面圆周数据。Yup和Ydown的最大值与最小值,即为圆柱体的最大半径Rmax与最小半径Rmin,评定圆度误差如下式所示:
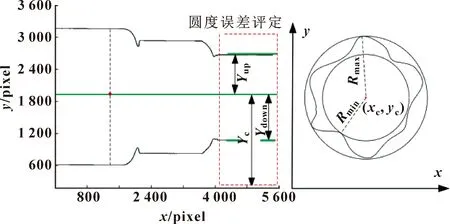
图8 圆度误差评定
eMZC=Rmax-Rmin
(11)
2.3 回转误差补偿
测量平台的旋转部件不可避免会存在回转误差,且测量精度越高其在测量整体误差中所占比例越大。文中通过旋转的方式测量空间直线度,借助已知参数的标准光轴对转台回转误差进行补偿。
将标准光轴按照相同的角增量θ旋转360°,并进行圆度测量。Pi(θ)表示第i步时的测量值,包含转台回转误差Ri(θ)和标准件形状误差Si(θ)。
Ri(θ)=Pi(θ)-Si(θ)
(12)
3 实验分析
通过对棋盘格进行角点检测,计算角点间的距离,测得此系统像素当量:K=0.016 mm/pixel。
(13)
式中:K为系统像素当量;S为相邻角点物理尺寸值;Pi为相邻角点像素数量。
在实验室条件下进行单拐曲轴(170F平键轴,30轴)的圆度误差评定,如图9所示。

图9 实验测量平台
曲轴按照固定增量2°进行旋转运动,在0~180°的行程内可采集90张间隔角度的旋转图像。相机在x方向的水平移动下,可对曲轴不同位置圆度误差进行测量。实验同时使用文中机器视觉测量方法(Machine Vision Measurement Method,MVM)和三坐标测量机 (Coordinate Measuring Machine,CMM)(行程范围800 mm×1 200 mm×600 mm)进行测量对比。以D3为例,数据处理结果如图10、11所示,测量数据如表1所示。
从表1和图12可以看出:在曲轴圆度误差测量对比实验中,MVM相较于CMM均值误差为6 μm,可以较准确测出曲轴圆度误差。同时,MVM的标准偏差和重复性误差都远小于CMM,可见基于机器视觉的圆度误差评定方法稳定性更为出色。
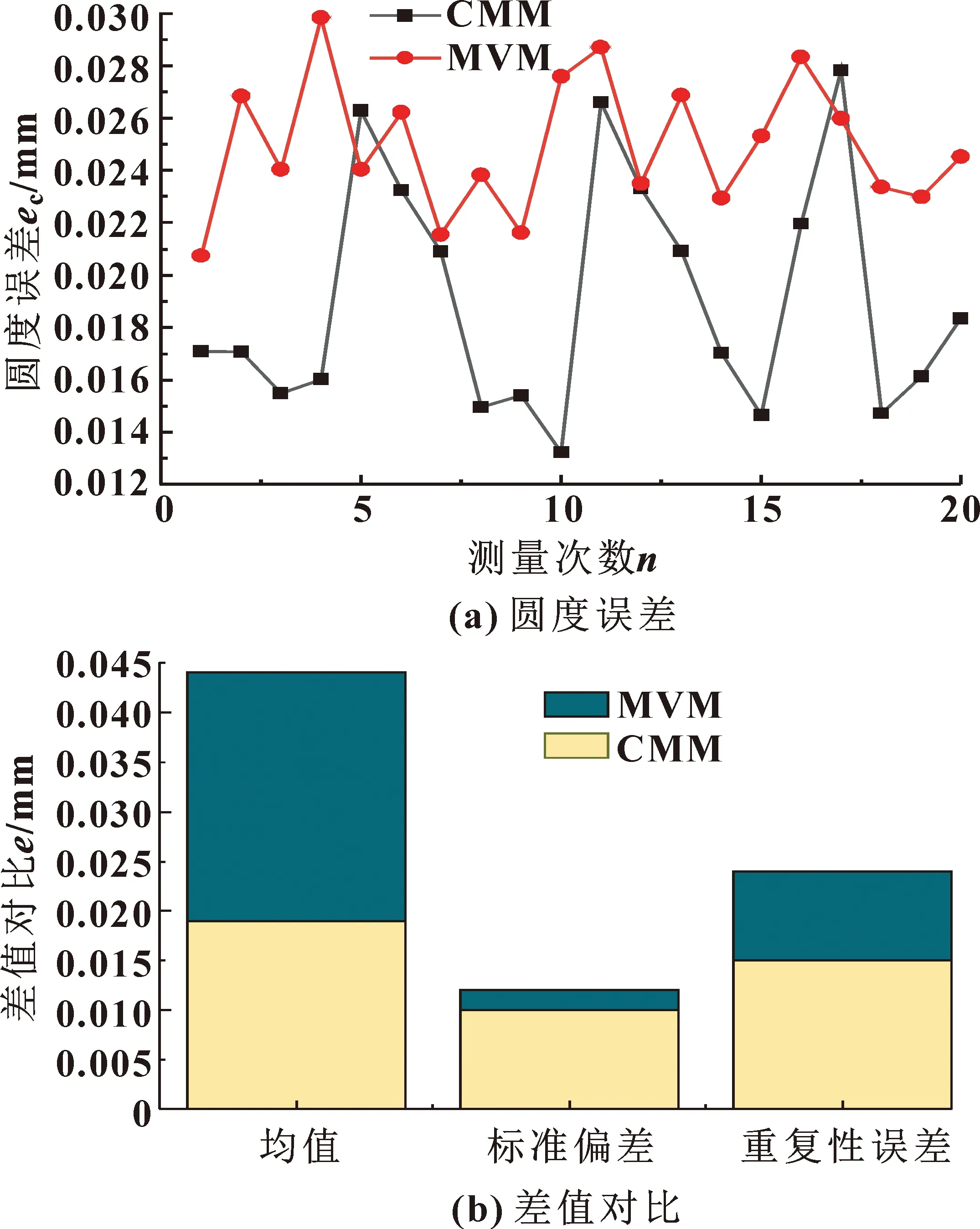
图12 测量数据对比
4 结论
利用相机代替传统检测工具,并重构曲轴截面圆周,提出一种基于机器视觉的曲轴圆度误差评定方法,主要优点是非接触。在曲轴轴径和圆度测量对比实验中,经与CMM对比,验证了视觉测量方案的准确性,表明文中测量评定方法可以实现曲轴圆度误差的精密测量。
