具有压差-位移检测装置的多路阀特性研究
2023-11-09赵冬杨敬
赵冬,杨敬
(太原理工大学机械与运载工程学院,山西太原 030024)
0 前言
多路换向阀作为多执行元件的中心控制元件,通过压力及流量双重控制实现对复杂液压系统不同执行机构的联合控制,在工程机械中的使用尤为广泛[1-2]。抗流量饱和负载敏感系统(LUDV)具有节能高效、精准可靠以及大流量情况之下仍然可以保持执行机构的协同工作等优点,在工程机械中得到大量的使用[3-4]。但是由于LUDV系统中的压力补偿阀以及附带的油路,仍然会带来节流压力以及沿程压力损失[5]。
LISOWSKI等[6]在不使用压力补偿阀及压力反馈传感器的情况下,仅通过改变滑阀阀口的形状,利用液动力实现了压力补偿。随着传感器和控制技术的发展,LUDV系统在进一步提高定位精度、稳定性、安全性以及节能方面表现出较大的研究空间,也使得以电控及阀口参数实时测量控制方式取代原有硬件压力补偿功能得以实现。国内学者对此进行了大量的研究。权龙[7]提出新的流量控制原理,仅用位移力反馈比例节流阀实现了流量与压差变化无关的单调线性控制。武宏伟[8]提出一种电子压力补偿流量匹配的新型液压系统,并对比了负载敏感压力补偿、电子压力补偿流量匹配、电液负载敏感3种系统的能耗情况。都佳等人[9]基于电子压力补偿提出了泵阀协同压力流量复合控制的液压系统。电子压力补偿的方式是基于压力电反馈、通过计算流量来实现阀芯位移的调节,具有精度高的特点,然而阀芯位移受到压力信号剧烈变化时容易发生振荡。
为了提高系统稳定性,本文作者通过压差-位移检测装置替代压力电反馈来检测压差,提高系统的阻尼从而降低阀芯的振荡[10]。首先利用AMESim仿真软件建立基于电子压力补偿流量匹配的泵阀协同复合控制系统仿真模型;然后建立具有该压差-位移检测装置的泵阀协同复合控制系统的仿真模型,通过仿真对压差-位移检测装置进行参数匹配,探讨各参数对系统特性的影响;之后对比具有压差-位移检测装置与单纯采用压力传感器对液压系统特性的影响。
1 压差-位移检测装置的工作原理
流体通过多路阀阀口的流量特性公式为
(1)
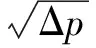
传统抗流量饱和负载敏感系统使用阀后压力补偿(压力补偿阀位于节流口后),通过梭阀将负载最高压力引到各联的压力补偿阀以及负载敏感泵的敏感腔,使多路阀各联的进出口压差Δp保持一个定值,Δp一般为1~2 MPa。根据式(1)可知:抗流量饱和系统的流量Q只与阀口的过流面积A呈单调线性关系[11-12]。
与传统抗流量饱和负载敏感系统不同,电子压力补偿首先经过压力传感器实时检测多路阀进出口压差Δp,然后通过改变阀芯位置补偿因压差变化产生的流量变化,使通过多路阀的流量不随负载压力变化。但由于压力传感器检测到阀口压差高频变化信号时会引起主阀芯振荡,而主阀芯振荡会引起流体的振荡,振荡的流体与阀芯形成非定常流固耦合效应,使得执行元件动态特性变差。所以文中在多路阀结构上取消了压力补偿器,采用电液比例泵取代了原先的负载敏感泵,在阀体上增加一个压差-位移检测装置。与电子压力补偿流量匹配系统相比,压差-位移检测装置取代了多路阀进口与出口安装的2个压力传感器,将多路阀前后的压差信号通过压差-位移检测装置转化成位移信号。控制器根据压差-位移装置的位移信号计算阀口流量,实时调节比例多路阀的阀口开度,从而实现压差补偿,提高了压差波动时抑制阀芯振荡能力。
该压差-位移检测装置主要由力比较活塞、压缩弹簧、位移传感器组成。模型及原理如图1所示。
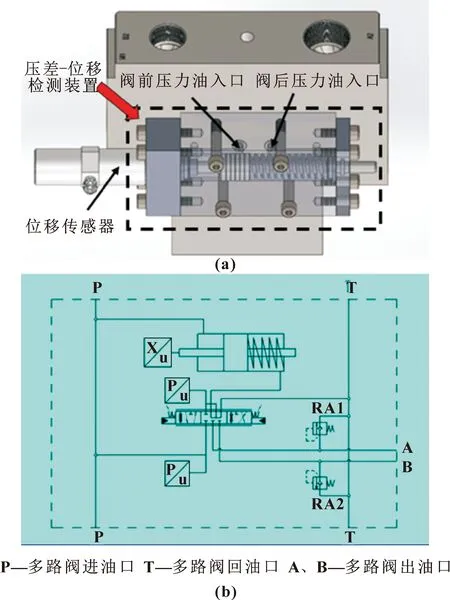
图1 模型(a)及其原理(b)
由图2可以看出:该装置近似为一个质量-弹簧-阻尼系统。力比较活塞和两腔的力平衡方程为
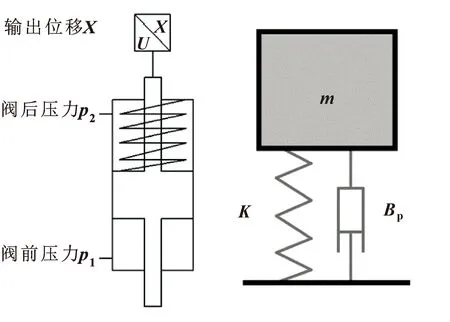
图2 装置简化图
(2)
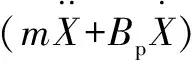
对式(2)进行拉普拉斯变换后为
Δp(s)A=ms2X(s)+BpsX(s)+KX(s)
(3)
得到阀进出口压差与输出位移的传递函数为
(4)
将上式化成标准形式为
(5)
(6)
输出位移
(7)
图3所示为系统框图。由公式(7)可知:文中所述压差-位移检测装置的力比较活塞位移取决于力比较活塞的有效面积A和质量m、压缩弹簧的弹簧刚度K以及黏性阻尼系数Bp。为了研究不同参数对系统的影响,需要初步确定压差-位移检测装置的基本参数。
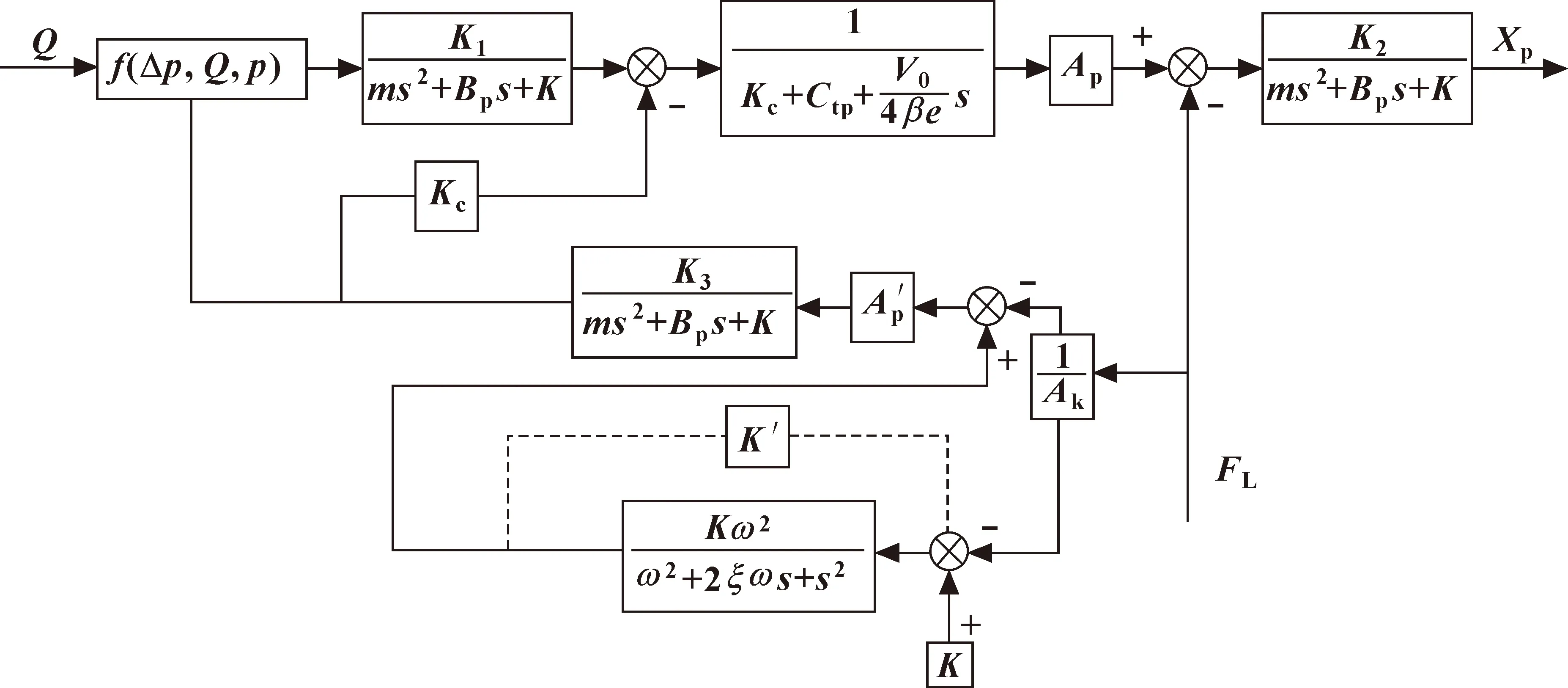
图3 系统框图
首先需要确定力比较活塞的有效面积A,有效面积取决于活塞的直径和杆径。忽略式(2)中质量m和黏性阻尼系数Bp对系统的影响后,力平衡方程为
ΔpA=KX
(8)
输出位移
X=AΔp/K
(9)
由式(9)可知:输出位移X主要取决于多路阀两端压差Δp、有效面积A和弹簧刚度K。因为输出流量只与阀口开度呈线性关系,需维持压差不变。为防止输出位移过大,需要减小有效面积A和增大弹簧刚度K。
考虑装置结构以及弹簧选型,初步确定力比较活塞直径为24 mm、杆径为10 mm。目前液控多路阀响应频率为30 Hz左右,根据典型节流口通流面积曲线确定阀芯微动区间的响应频率为50 Hz左右,以此作为压差-位移检测装置的转折频率。假设压缩弹簧刚度为30 N/mm,用式(6)可初步估算力比较活塞质量为0.2 kg。
2 电子压力补偿泵阀协同复合控制系统AMESim仿真模型的建立和验证
2.1 泵阀协同压力流量复合控制系统AMESim仿真模型的建立
通过AMESim仿真软件建立图4所示电子压力补偿的泵阀协同复合控制系统仿真模型。它由多路阀主阀芯、流量补偿器、负载以及电液比例泵组成。在比例多路阀入口和出口分别安装压力传感器以实时检测进出口压差数据,经流量补偿器从而实现泵阀协同复合控制。图5所示为多路阀的主阀芯实物。根据实物图的尺寸对模型中的主阀芯模型参数进行设定,其他模型参数按照表1进行设置。

表1 仿真模型参数
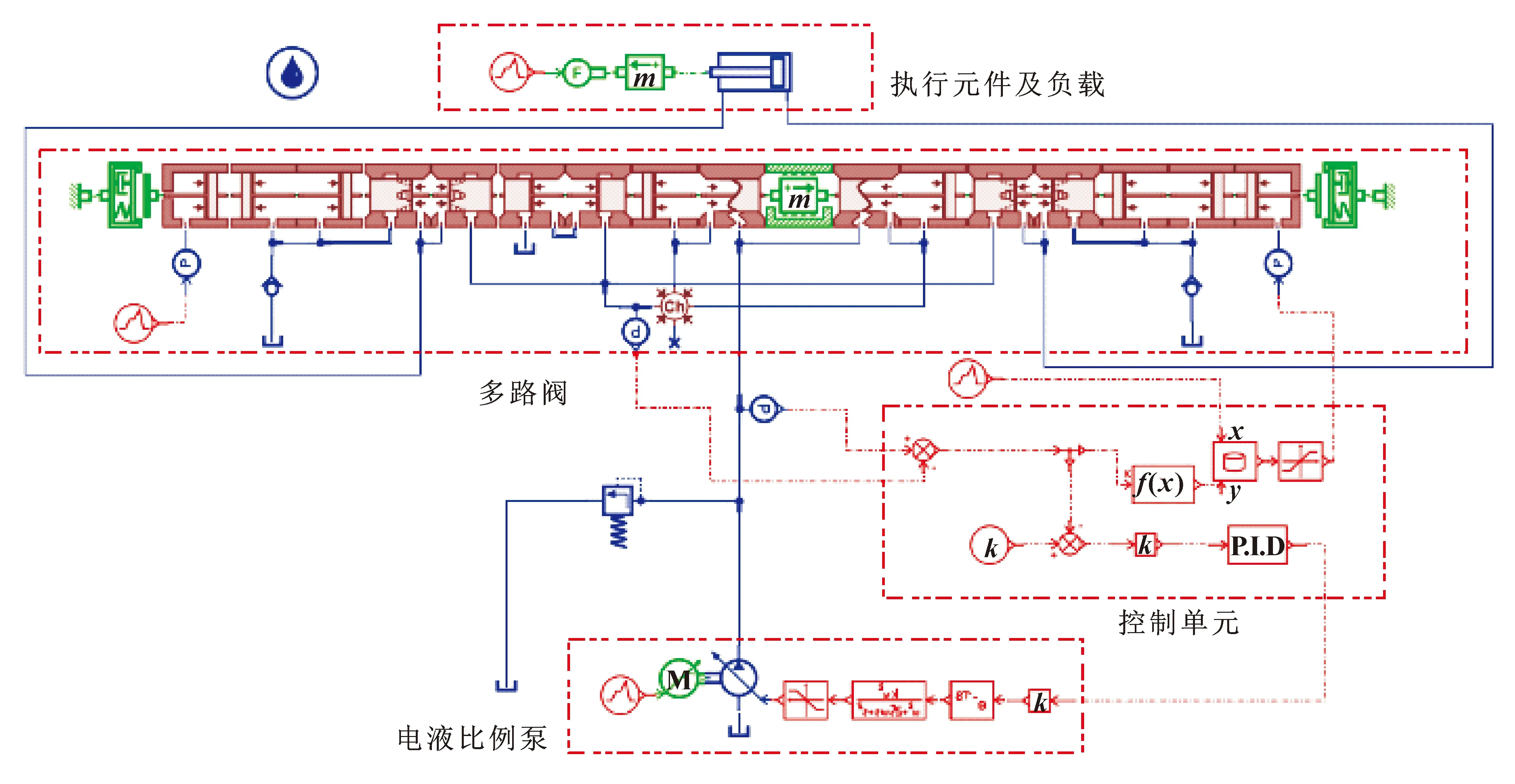
图4 电子压力补偿泵阀协同复合控制系统AMESim仿真模型

图5 多路阀阀芯实物
2.2 试验验证
为了验证建立的起重机泵阀协同复合控制系统仿真模型的准确性,搭建了图6所示的多路阀试验平台。电液比例泵恒定转速为1 900 r/min,比例溢流阀调定电液比例多路阀的阀后压力为负载压力1.2 MPa;先导油腔内的压力取0.8、1.2、1.6 MPa。主阀压力损失试验与仿真结果对比如图7所示。

图6 多路阀试验平台
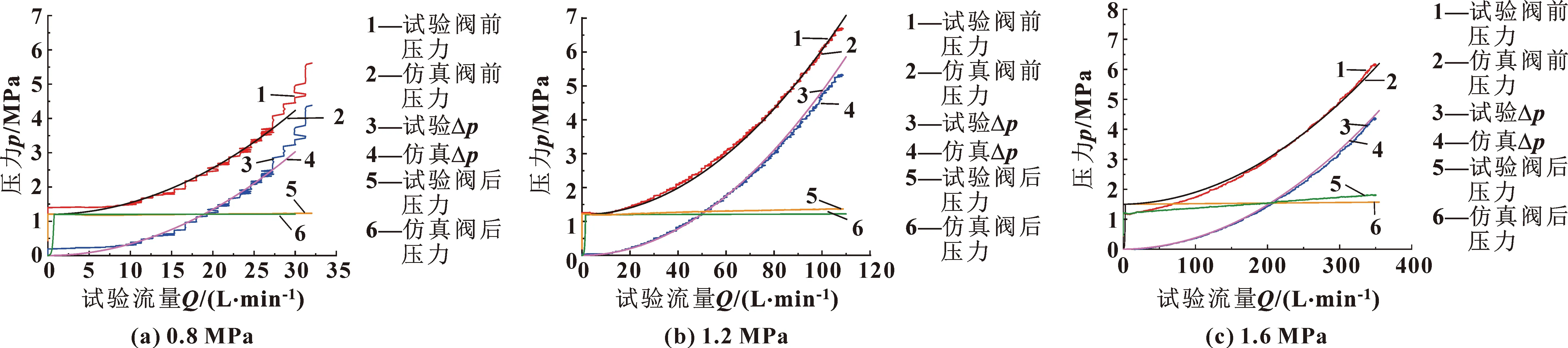
图7 不同先导压力时的主阀压力损失
在各个阀口开度下,仿真与试验的控制特性曲线均能较好地吻合,试验的阀前、后压差与仿真结果基本吻合,证明了建立的大流量电液比例换向阀AMESim模型的准确性。
为验证电液比例泵模型的准确性,对电液比例泵进行动静态特性测试。电液比例泵实物如图8所示。静态特性测试设置电液比例泵的电机转速为1 900 r/min,比例溢流阀调定负载压力的数值为16 MPa。输入手柄信号先从0逐渐增大至700 mA,再从700 mA逐渐降至0,液压泵静态特性曲线如图9所示。动态特性测试设置电液比例泵的电机转速为1 900 r/min,比例溢流阀调定负载压力的数值为1 MPa,手柄信号先从0阶跃变化至500 mA,保持一段时间后手柄信号由500 mA阶跃变化至300 mA,之后手柄信号在500 mA和300 mA之间,先保持一段时间再进行阶跃式的变换。液压泵阶跃响应特性曲线如图10所示。

图8 电液比例泵实物
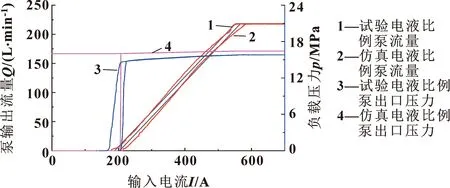
图9 负载压力为16 MPa时泵的静态特性曲线
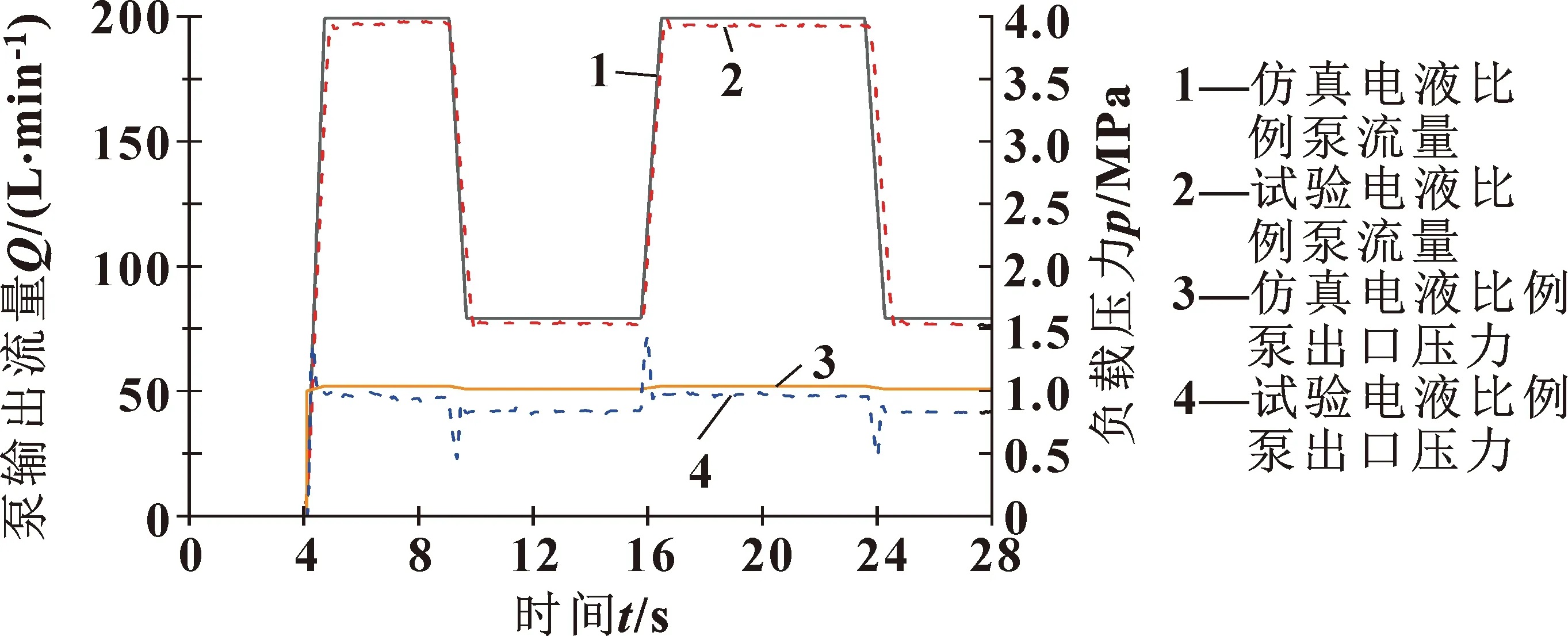
图10 负载压力为1 MPa时泵的阶跃特性曲线
由图9、10可知:试验中的负载压力与设定和仿真存在一定的差异,这是由于实际的溢流阀的启闭特性所造成的。由电液比例泵的试验和仿真结果可知:仿真与试验的输出流量曲线能较好地吻合,说明所建立的仿真模型能比较准确地代表实际的电液比例泵。
3 具有压差-位移检测装置的泵阀协同复合控制系统的AMESim仿真模型的建立与参数匹配研究
3.1 压差-位移检测装置的AMESim仿真模型的建立
根据上节压差-位移检测装置的结构与工作原理,利用AMESim仿真软件中的HCD液压元件设计库建立压差-位移检测装置的AMESim仿真模型,如图11所示。模型中加入单向阀元件的目的是防止阀后压力在某一时刻大于阀前压力时,力比较活塞反向输出位移。
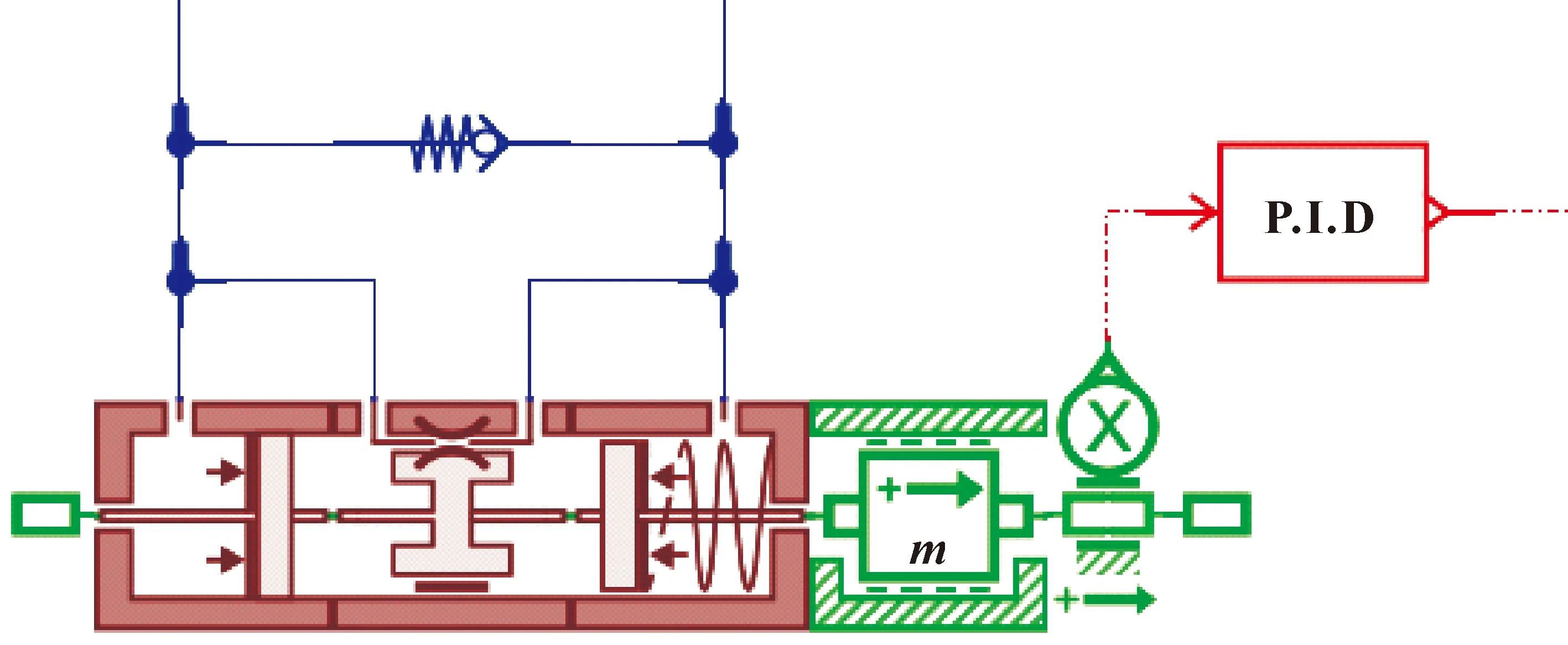
图11 压差-位移检测装置仿真模型
3.2 具有压差-位移检测装置的泵阀协同复合控制系统的AMESim仿真模型的建立
使用AMESim仿真软件建立图12所示的具有压差-位移检测装置的泵阀协同复合控制系统的AMESim仿真模型,包括电液比例泵、比例多路阀、变幅油缸、压差-位移检测装置。根据力源L11VO115L型轴向双联电液比例柱塞泵样本建立液压泵仿真模型。根据起重机变幅油缸的工作特性,在变幅油缸伸出的过程中,负载压力随之减小,因此负载模型设置压力信号在1 s内从120 000 N减小到100 000 N。系统仿真时间为5 s,时间步长为0.001 s。压差-位移检测装置参数设置见表2。

表2 压差-位移检测装置参数
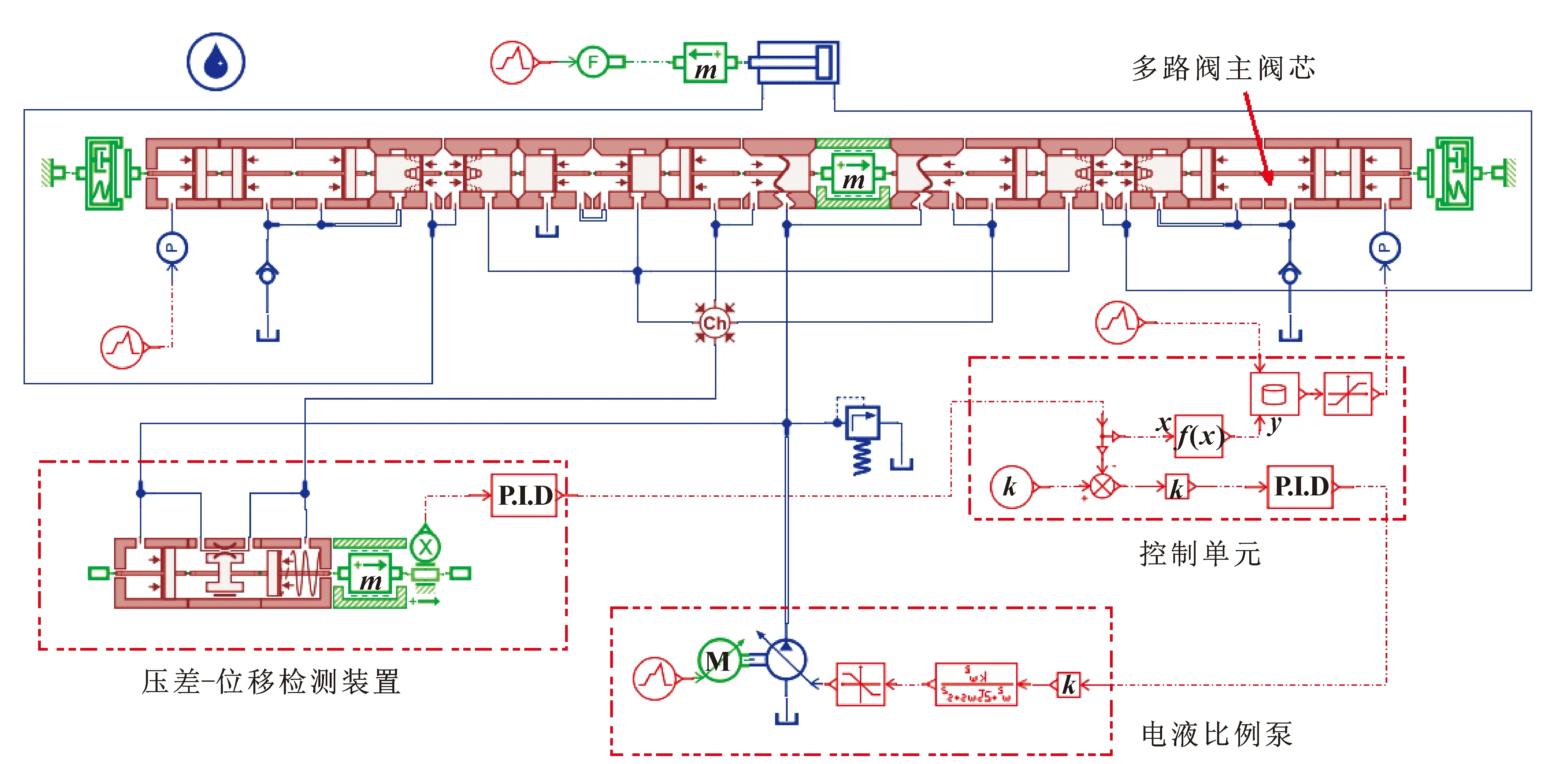
图12 具有压差-位移检测装置的泵阀协同复合控制系统的AMESim仿真模型
3.3 压差-位移检测装置各参数对系统特性的影响
通过AMESim仿真软件的批处理功能模块,分别研究多路阀压差-位移检测装置在不同弹簧刚度K、不同力比较活塞质量m、不同黏性阻尼系数Bp下对多路阀系统特性的影响[14]。液压泵输出最大压力为28 MPa。设定输入流量信号为80 L/min,其他参数相同,运行仿真。
3.3.1 不同弹簧刚度对系统的影响
通过批处理功能设定弹簧刚度K分别为10、20、30 N/mm。为使多路阀前后的压差保持在2 MPa,经计算将压差-检测装置的比例环节分别设定为0.26、0.53、0.81。仿真结果如图13所示。系统响应性能指标对比如表3所示。
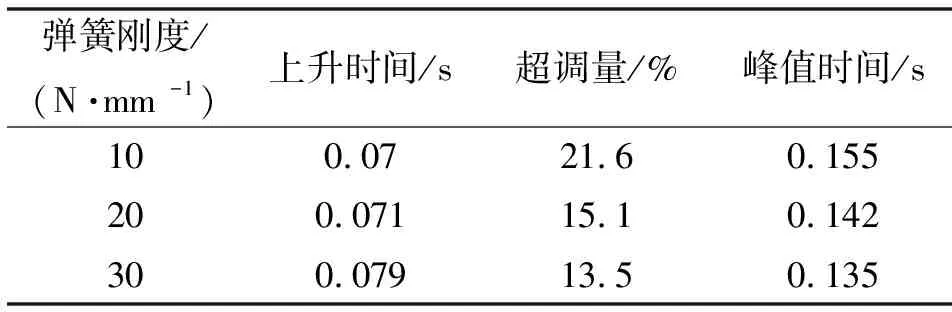
表3 响应性能指标对比(不同弹簧刚度)
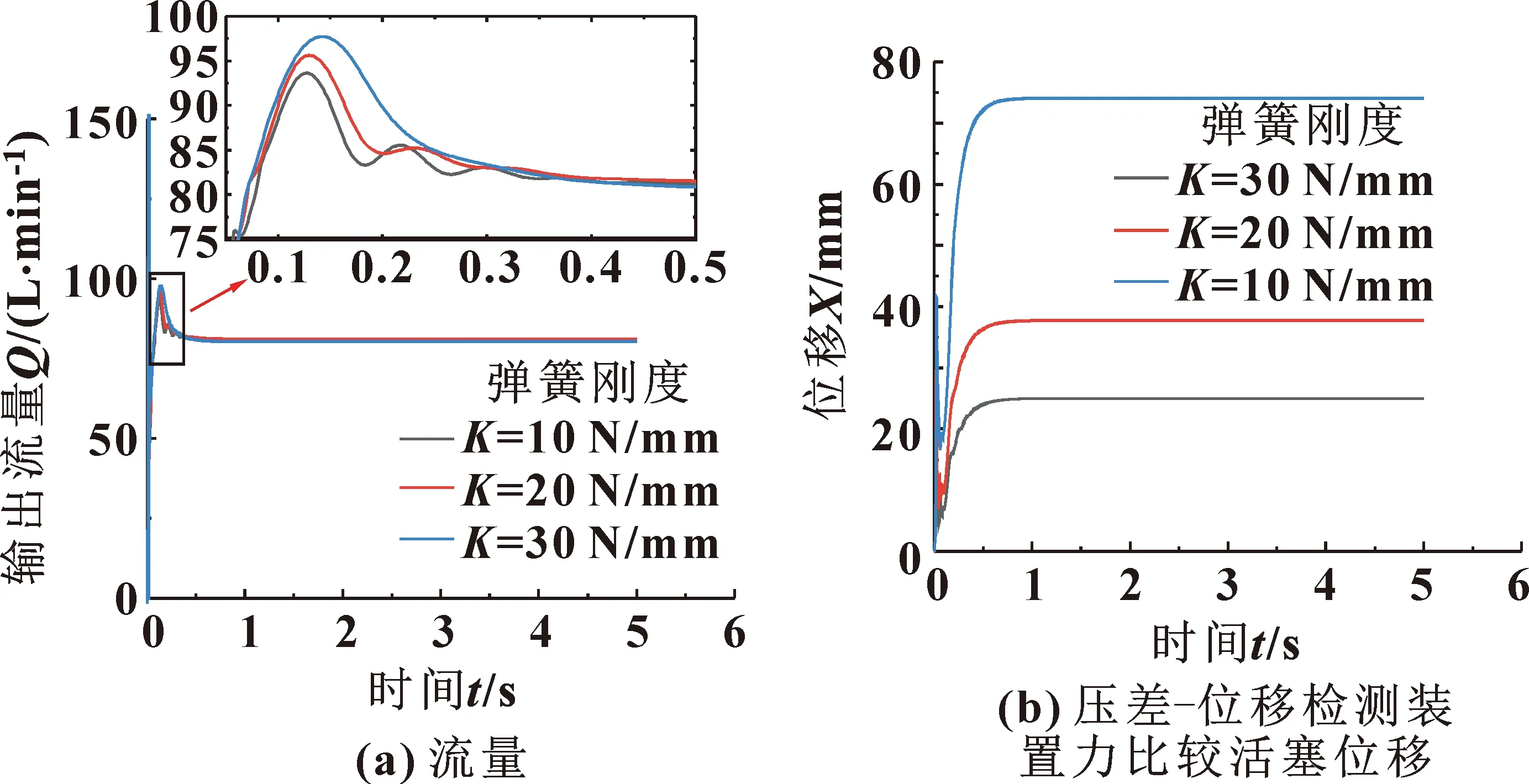
图13 不同弹簧刚度的仿真曲线
从图13(a)中可以看出:压差-位移检测装置的弹簧刚度对系统的动态响应影响较大。可知:随着弹簧刚度从10 N/mm增加到30 N/mm时,系统的上升时间变化了0.009 s,系统的峰值时间变化了0.02 s,系统的超调量变化了8.1%。从图13(b)中可以看出:不同的弹簧刚度对应不同的力比较活塞位移,随着弹簧刚度K的增加,力比较活塞的位移随之减小。适当增加弹簧刚度对于压差-位移检测装置的小型化和减少成本具有一定的帮助。
3.3.2 不同活塞质量对系统的影响
通过批处理功能设定力比较活塞的质量m分别为0.2、0.25、0.3 kg,弹簧刚度设定为30 N/mm,黏性阻尼系数设定为50 N·s/m,其他参数相同,运行仿真,结果如图14所示。系统响应性能指标对比如表4所示。
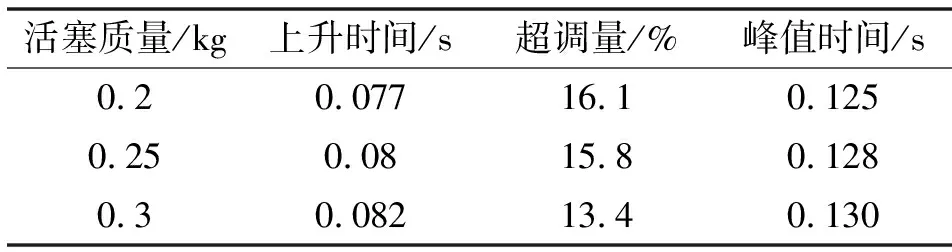
表4 响应性能指标对比(不同活塞质量)
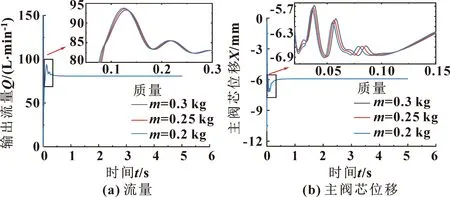
图14 不同活塞质量的仿真曲线
从图14和表4可知:在压缩弹簧刚度和黏性阻尼系数Bp相同的条件下,随着力比较活塞的质量由0.2 kg增加到0.3 kg,上升时间变化了0.005 s,峰值时间变化了0.005 s,超调量减小了2.7%。因此力比较活塞的质量对系统特性的影响较小。
3.3.3 不同黏性阻尼系数对系统的影响
通过批处理功能设定黏性阻尼系数Bp分别为50、100、150 N·s/m。弹簧刚度设定为30 N/mm,活塞质量设定为0.2 kg。仿真时间为5 s,时间步长为0.001 s。其他参数相同,运行仿真,结果如图15所示。系统响应性能指标对比如表5所示。
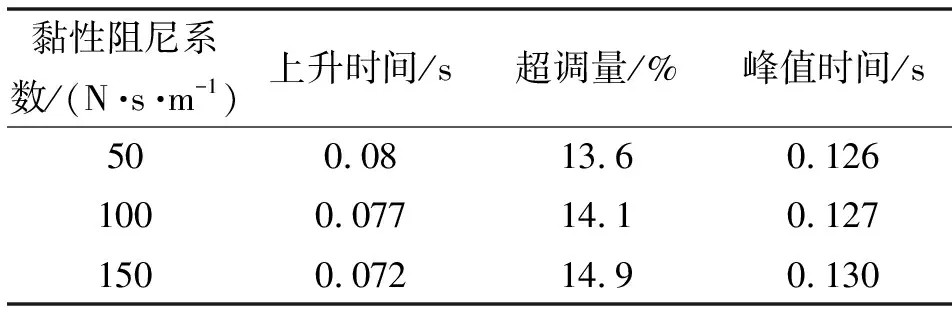
表5 响应性能指标对比(不同黏性阻尼系数)
从图15和表5中可知:在弹簧刚度和力比较活塞质量不变的条件下,随着黏性阻尼系数从50 N·s/m增加到150 N·s/m,上升时间变化了0.008 s,峰值时间变化了0.004 s,超调量变化了1.3%。因此黏性阻尼系数越大,上升时间越小和超调量越大。
最终弹簧刚度K、力比较活塞质量m和黏性阻尼系数Bp参数的确定需要考虑弹簧选型、与活塞内腔的干涉以及活塞长度等因素。因为确定压差-位移检测装置的转折频率为50 Hz,所以压缩弹簧的弹簧刚度K与力比较活塞的质量m一一对应。经过仿真对比在50、100、150 N·s/m 3种黏性阻尼系数下的仿真结果,选取超调量作为对比的指标。
根据表6,序号3所对应的超调量最小。最终确定弹簧刚度为30 N/mm,力比较活塞质量为0.3 kg,黏性阻尼系数为50 N·s/m。
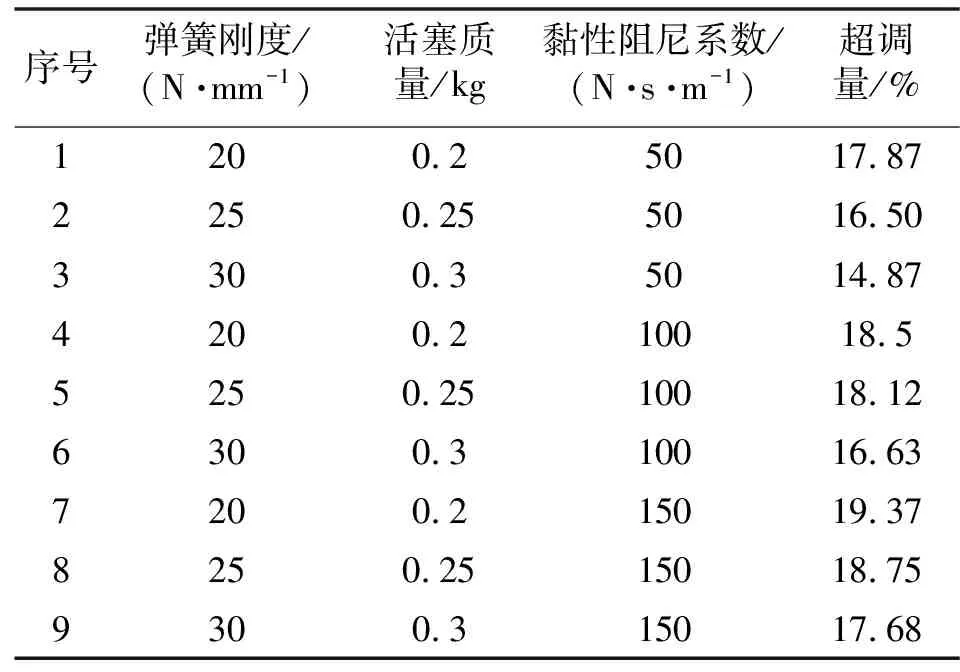
表6 不同黏性阻尼系数下仿真结果对比
3.4 对比分析
为对比有无压差-位移检测装置的条件下多路阀主阀芯的振荡情况,负载压力输入为正弦信号和信号的叠加,信号初始值为100 000,振幅为20 000,频率分别设置为20、30、40、50、60、70、80 Hz。
设定系统仿真运行时间为5 s,时间步长设置为0.001 s。运行仿真,负载频率为20、30、40 Hz时,液压系统输出流量与主阀芯位移曲线如图16所示。负载频率为50~80 Hz负载液压系统流量与主阀芯位移曲线如图17所示。
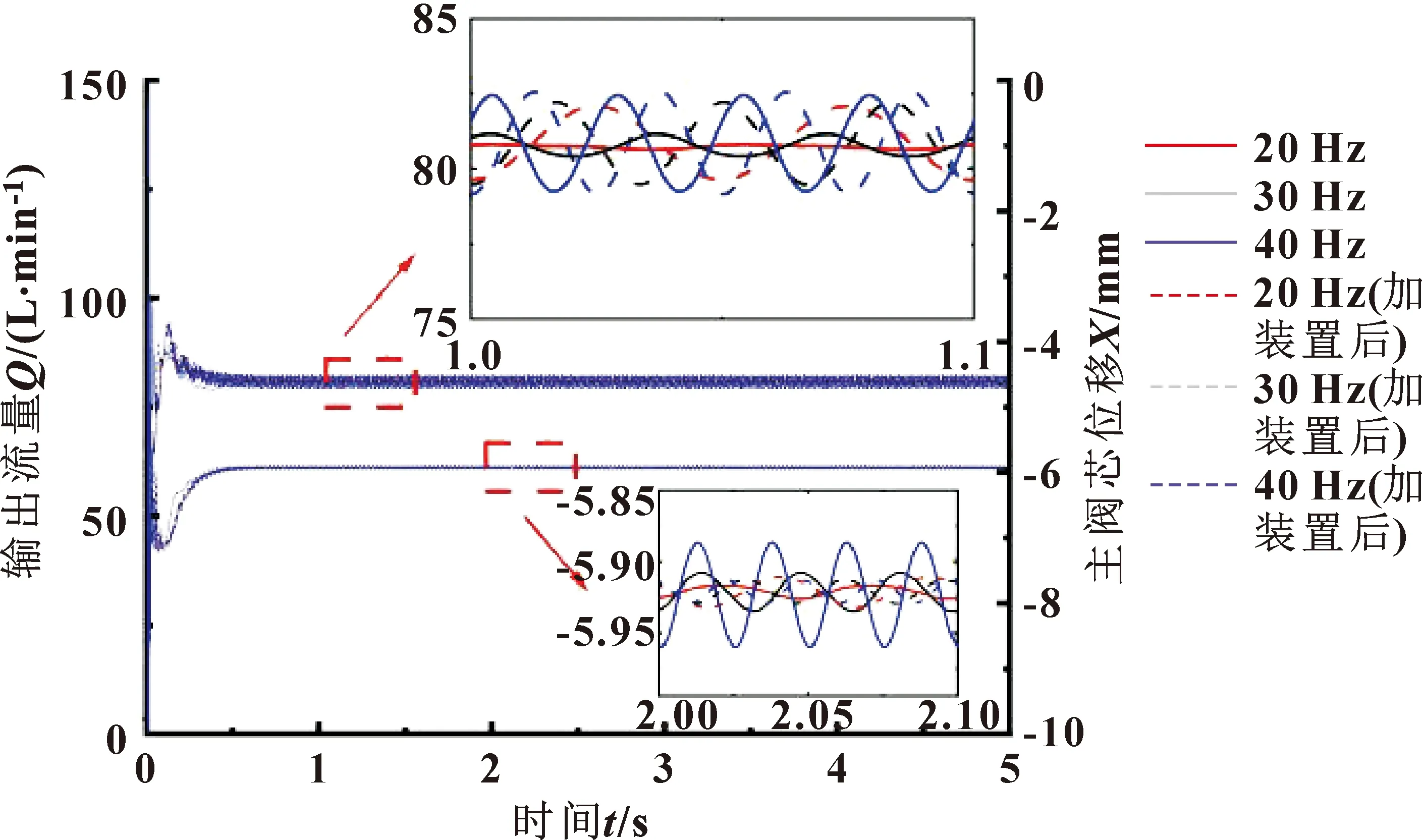
图16 负载频率为20~40 Hz液压系统输出流量与主阀芯位移曲线
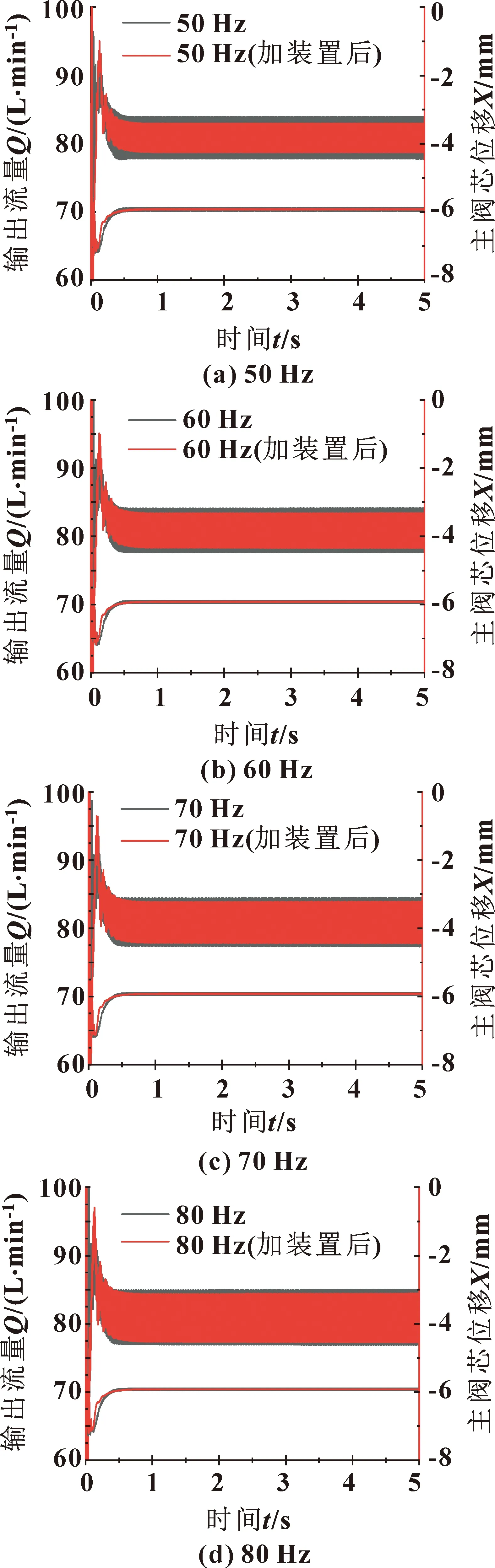
图17 不同负载频率下液压系统输出流量与主阀芯位移曲线
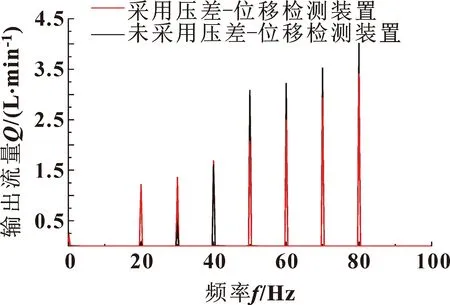
图18 负载频率为20~80 Hz液压系统输出流量FFT曲线
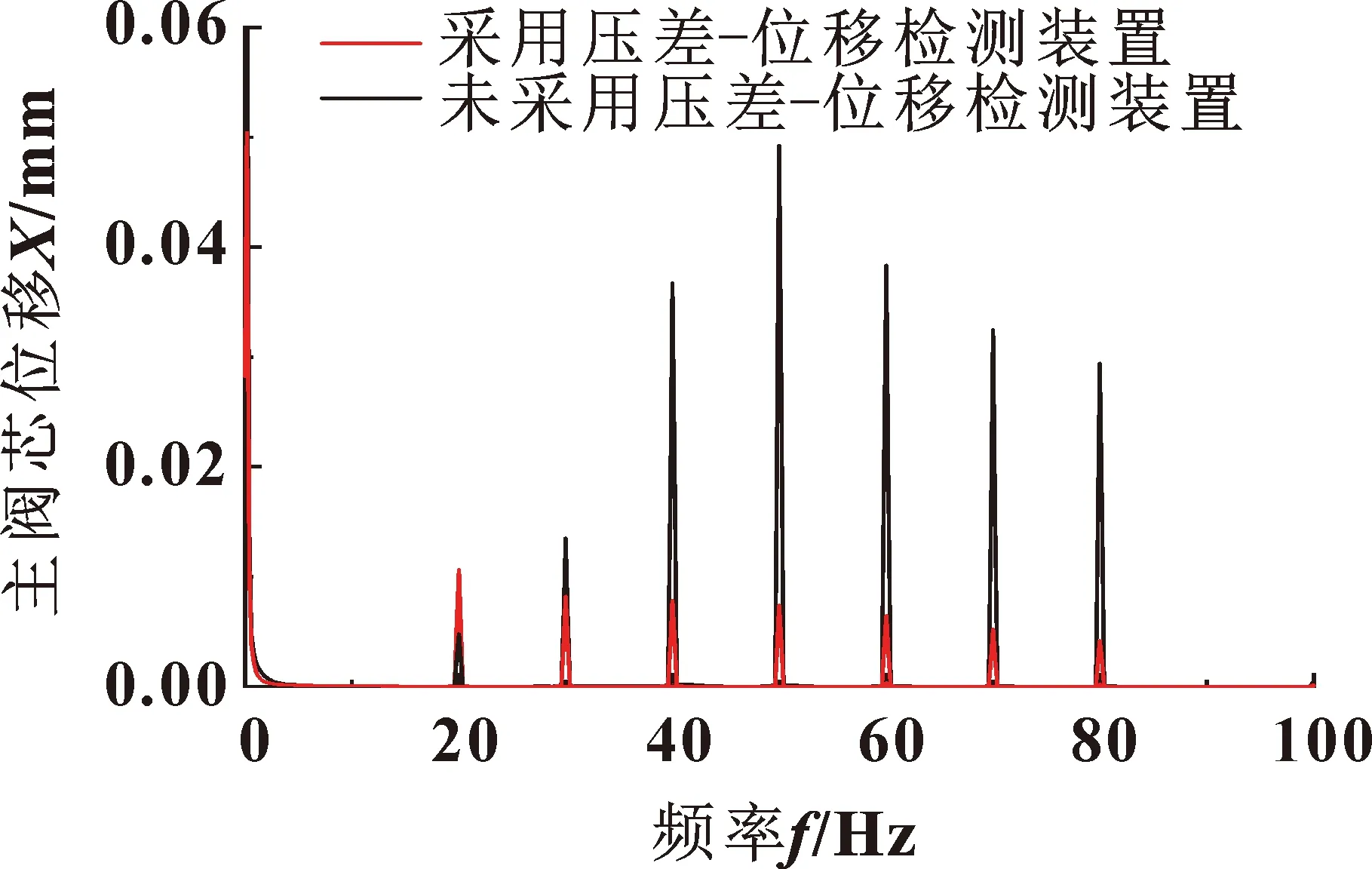
图19 负载频率为20~80 Hz时主阀芯位移FFT曲线
从图16—19中可以看出:当负载频率小于50 Hz时,采用压差-位移检测装置的系统的输出流量相较不稳定和不准确,但是主阀芯的振荡得到了一定程度的抑制。负载频率为20 Hz时,输出流量振荡幅度增大了15倍,主阀芯振荡增大了1倍。负载频率为30 Hz时,输出流量振荡幅度增大了27%,主阀芯振荡减小了38%。负载频率为40 Hz时,输出流量振荡增大了4%,主阀芯振荡减小了73%。
从图17—19中可以看出:当负载频率大于50 Hz时,采用压差-位移检测装置的系统输出流量相较变得更加稳定和主阀芯振荡的问题也会得到抑制。负载频率为50 Hz时,输出流量振荡减小了30%,主阀芯振荡减小了85%。负载频率为60 Hz时,输出流量振荡减小了21%,主阀芯振荡减小了84%。负载频率为70 Hz时,输出流量振荡减小了17%,主阀芯振荡减小了84%。负载频率为80 Hz时,输出流量振荡减小了15%,主阀芯振荡减小了86%。
4 结论
通过对压差-位移检测装置的弹簧刚度、活塞质量以及黏性阻尼系数3个参数分别进行仿真分析,得到结论:该装置压缩弹簧的弹簧刚度、黏性阻尼系数以及力比较活塞质量对系统特性的影响依次减小。通过对比有无压差-位移检测装置时系统特性的不同结果可知:当负载频率以及压力波动小于50 Hz时,采用压力电反馈的控制方式可以保证流量的稳定以及准确。当负载频率以及压力波动在50~80 Hz时,采用压差-位移检测装置,输出流量的波动减小了15%~30%,主阀芯的振荡减小了约85%。
