某型柴油机润滑油原子发射光谱分析经验阈值研究

吴善跃，陈 昕，任凤华，吕 跻

（92957部队，浙江 舟山 316000）

润滑油原子发射光谱分析在船舶动力机械状态监测领域得到了日益广泛应用[1-2]。然而，在实际应用中面临着缺乏明确判别阈值问题，极大制约了油液监测工作深入开展。针对该问题，有必要根据科学理论，利用积累的历史数据统计经验阈值，来指导监测工作开展。对于动力机械原子发射光谱分析监测阈值制定，现已形成多种分析方法，其中三线值法应用最为广泛［1-5］。这些方法的使用有一基本前提，即要求样本应符合正态分布。对于原子发射光谱分析非正态分布样本数据应如何统计经验阈值，文献[5-6]对传统方法做出了改进，但要求样本数据符合t分布。文献[7]所述最大熵值法实质上是一种基于分位数的阈值确定方法，虽对样本分布没有要求，分析简单，但忽略了样本分布规律，所确定阈值较粗糙。

笔者编制某型船用发电柴油机原子发射光谱分析经验阈值时，在大样本分析中发现多数元素样本并不符合正态分布要求，前文所述方法均存在一定局限性。为此，本文拟以该型机为研究对象，分析样本分布规律，探讨不同分布规律样本数据处理及阈值统计方法。

1 原始样本分析

某型船配置有4 台同型发电柴油机，为编制该型船发电柴油机油液光谱分析经验阈值，收集13艘船52 台发电柴油机油液光谱数据，共计1 741条。对上述原始样本，采用频数直方图形式分析质量分数分布。绘制频数直方图时，先获取样本中最大质量分数并取整（记为Xmax），并以该整数作为样本分组数，其分组集合为：

按以上分组绘制主要磨损元素和污染元素质量分数分布频数直方图，图1～图5为各元素质量分数分布频数直方图，分析直方图可发现：①镁元素近似正态分布，而其它元素均为非正态分布；②铁元素近似为对数正态分布；③铝、铬、铜、铅、镍元素分布近似钟形曲线一半；④钠元素为不拘分布，呈明显双峰形态；⑤镍、锡、银、硼元素为不拘分布，高度集中于零值附近。上述元素质量分数分布具有明显右拖尾现象，不仅出现零散分布，而且数值极大，尤其是钠、镁元素。

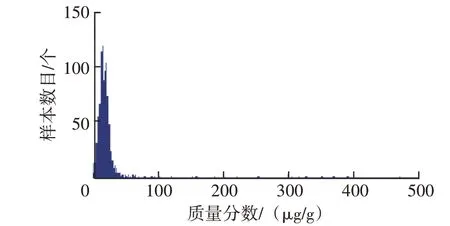
图1 镁元素质量分数分布频数直方图

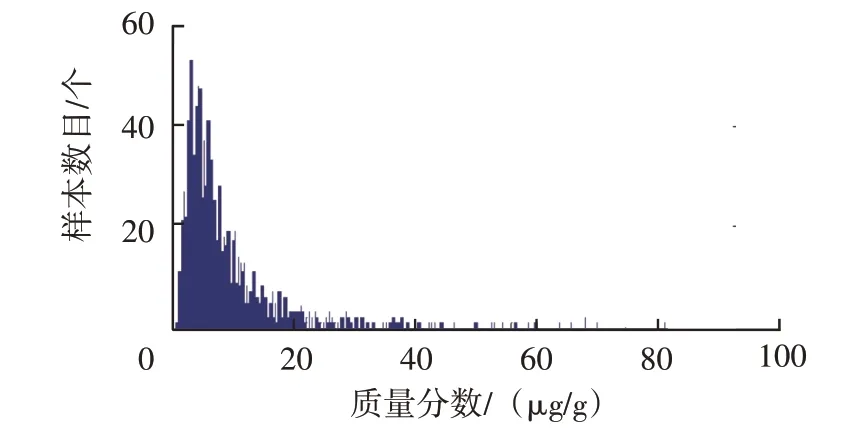
图2 铁元素质量分数分布频数直方图

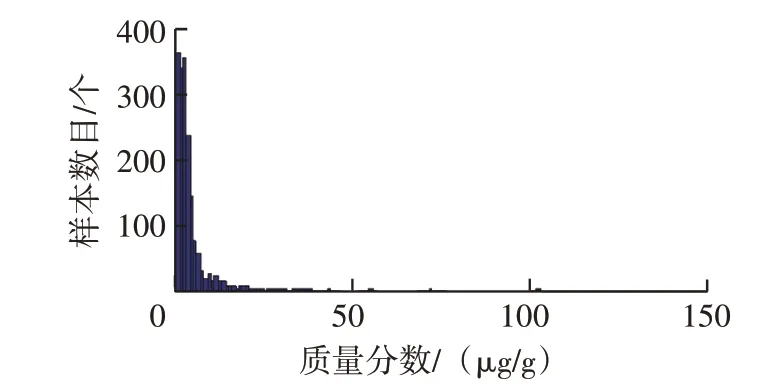
图3 铝元素质量分数分布频数直方图

图4 钠元素质量分数分布频数直方图

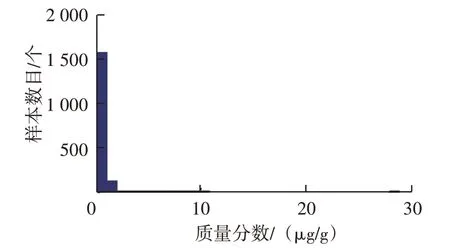
图5 镍元素质量分数分布频数直方图

2 数据处理与阈值统计

图1～图5 代表了5 种不同分布规律原始样本频数直方图，以下分别论述数据处理与阈值统计。

2.1 镁元素

镁元素分布基本呈正态分布，符合三线值方法使用前提。原始样本均值（Xˉ）与均方差（S）分别为21 μg/g 和27 μg/g，以此分别作为正态分布参数μ和σ，绘制正态分布密度函数曲线，用于拟合图1对应频率直方图，镁元素原始样本概率密度拟合曲线见图6。由图6 可知，该正态分布密度函数曲线并不能理想地拟合频率直方图，两者之间存在较大差异。而以此正态曲线为基础确定的三线值法预警阈值（μ+2σ）、报警阈值（μ+3σ）分别为75.0 μg/g和102.0 μg/g，数值明显过大。

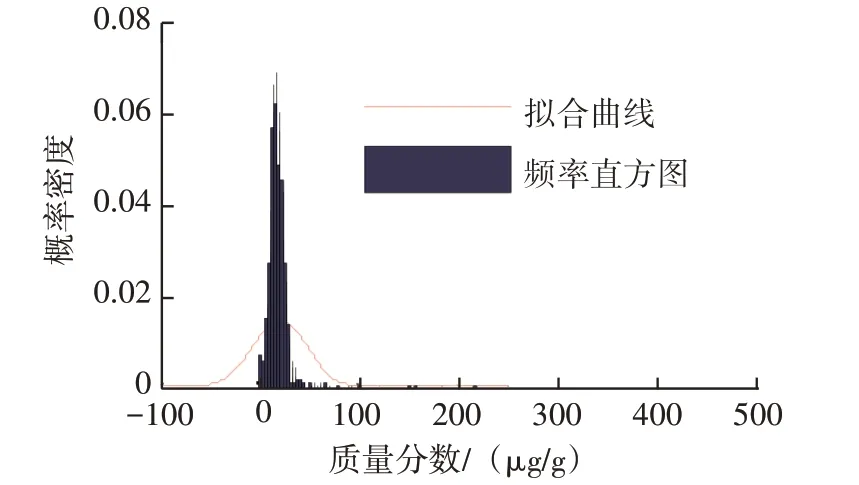
图6 镁元素原始样本概率密度拟合曲线

造成以上问题的基本原因在于样本中具有少数零散极大值数据（最大高达463 μg/g），它们对样本均方差统计具有较大不利影响，应按一定的法则进行合理筛除。基于Xˉ+ 3S的数据筛除循环流程见图7，本文采用图7 筛除极大值数据，其目的是使筛除后的样本均聚集于均值的3倍均方差范围内，更符合正态分布。

图7 基于X+3S的数据筛除循环流程

根据图7 筛除原始样本中极大值数据。其中，变量赋初值情况如下：NMg为463.0 μg/g，MMg为1.0 μg/g 。流程结束时确定的筛除界限值为37.0 μg/g。筛除掉的极大值数据有64 个，约占总数的3.68%。筛除极大值数据后，计算Xˉ、S分别为17.8 μg/g 和6.4 μg/g，以此分别作为正态分布参数μ和σ，绘制正态分布密度函数曲线，就可得到筛除数据后镁元素概率密度拟合曲线见图8。

图8 筛除数据后镁元素概率密度拟合曲线

由图8 可知，正态分布密度函数曲线较好拟合了频率直方图。根据图8确定的正态分布概率密度曲线，可确定镁元素质量分数预警阈值（μ+2σ）、报警阈值（μ+3σ）分别为30.6 μg/g 和37.0 μg/g，远小于图6的相关阈值。

2.2 铁元素

设铁元素质量分数原始样本集合为{ }Xi，对该集合元素进行对数处理后变为集合{ }Yi，其中：

式中，X0为无量纲化处理的基准值，取1 μg/g。

集合{Yi}中最大值为1.96，从0～2.0 以0.05 为间隔将集合{Yi}分为40 组，并以频数直方图形式显示集合{Yi}，铁元素原始样本对数处理后的频数直方图见图9。

图9 铁元素原始样本对数处理后的频数直方图

可采用正态分布密度函数曲线拟合图9 对应的频率直方图。考虑到图9 中略微存在右拖尾现象，采用图7 中流程筛除图9 中极大值数据。其中，变量赋初值情况如下：NFe为1.90，MFe为0.01。流程结束时确定的界限值为1.70。筛除掉的极大值数据有16个，占总数的0.92%。

筛除极大值数据后，计算Xˉ、S的值分别为0.87 和0.28，以此分别作为正态分布参数μ和σ，绘制正态分布密度函数曲线，将该曲线作为频率直方图的拟合曲线，对数处理和筛除数据后铁元素概率密度拟合曲线见图10。

图10 对数处理和筛除数据后铁元素概率密度拟合曲线

由图10 可知，正态分布密度函数曲线较好拟合了频率直方图，故可以由正态分布参数μ和σ确定阈值。所计算的预警阈值（μ+2σ）、报警阈值（μ+3σ）分别为1.42 和1.70，对应于对数变化前的原始值分别为26.3 μg/g、50.1 μg/g，由此最终确定这2个原始值分别为铁元素质量分数的预警阈值和报警阈值。

2.3 铝元素

铝元素分布近似钟形曲线一半（钟形曲线左右对称点数值为零），可考虑在正态分布密度函数曲线基础上构建拟合分布密度函数g(x)。g(x)定义为分段函数：

式中，f(x)是均值为0的正态分布密度函数，即：

设g(x)对应的分布函数为G(x)，即：

当x→∞时，G(x) = 1。g(x)可视为f(x)负半轴部分按零轴对称叠加到正半轴部分。由以上各式关 系 不 难 计 算G(2σ)、G(3σ) 分 别 为0.954 4 和0.997 4，可将2σ、3σ分别作为报预警阈值和报警阈值。

半钟形分布数据筛除循环流程如图11 所示。由于图3样本中存在零散极大值数据，按图11流程筛除极大值数据。其中，变量赋初值情况如下：NAl为104.0 μg/g，MAl为1.0 μg/g。

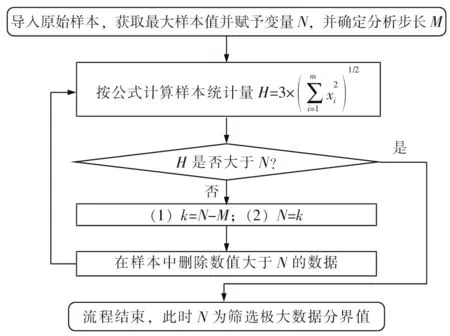
图11 半钟形分布数据筛除循环流程

流程结束时筛除极大值数据的界限值为11.0 μg/g。筛除掉极大值数据112 个，约占总数的6.43%。针对筛除极大值数据后样本，计算2 阶原点矩平方根为3.5 μg/g，将其作为参数σ，绘制f(x)、g(x)函数曲线，铝元素概率密度拟合曲线如图12 所示。由图12 可知，g(x)能较好拟合频率直方图，2σ、3σ的计算值为7.0 μg/g和10.5 μg/g，把该值作为预警阈值和报警阈值。

图12 铝元素概率密度拟合曲线

2.4 钠元素

图4 中钠元素分布具有数值极大的零散数据（最大为3 479.0 μg/g），先采用图7 流程进行极大值数据筛除。其中，变量赋初值情况如下：NNa为3 479.0 μg/g，MNa为1.0 μg/g 。流程结束时筛除极大值数据的界限值为182.0 μg/g。筛除掉的极大值数据有102 个，约占原始样本的5.8%。筛除数据后钠元素频数直方图如图13 所示，样本分布不仅与正态分布相差甚远，而且具有2 个明显聚集区域（分别为0～40.0 μg/g 和70.0～120.0 μg/g）。该样本属于不拘分布，无法使用常见分布密度曲线拟合频率分布直方图。只能直接采用分位数法确定阈值。

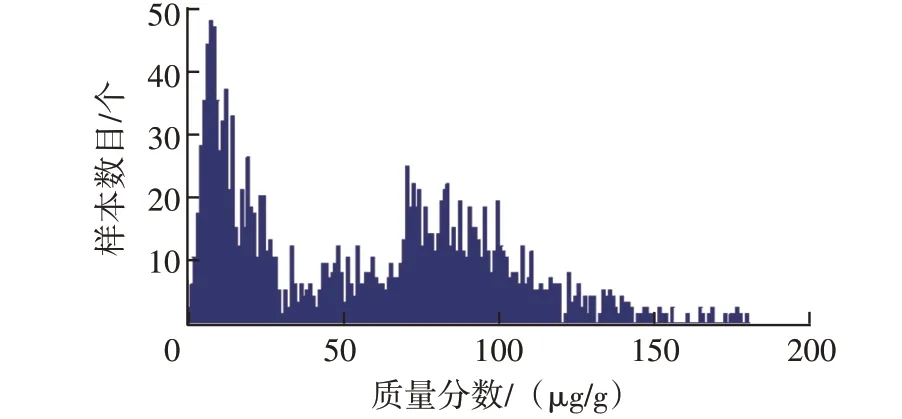
图13 筛除数据后钠元素频数直方图

考 虑 到 在 正 态 分 布 中 区 间[-∞，μ+ 2σ]、[-∞，μ+ 3σ]对应的概率为97.72%和99.87%，可将图13样本中97.72%、99.87%分位数设为预警阈值和报警阈值，分别对应为139.7 μg/g、182.0 μg/g。

2.5 镍元素

考虑到图5 样本高度集中于零值附近，参考图12 流程进行极大值数据筛选。变量赋初值情况如下：NNi为29.0 μg/g，MNi为0.1 μg/g。流程结束时，确定的极大值数据界限值为1.0 μg/g。筛除掉的极大值数据160 个，占总数的9.19%。筛除极大值数值后，在0～1.0 μg/g区间内以0.1 μg/g为间隔显示样本频数直方图，筛除数据后镍元素频数直方图见图14。

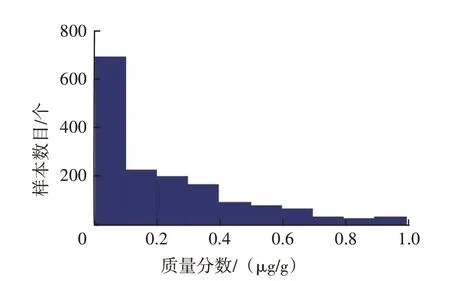
图14 筛除数据后镍元素频数直方图

该样本属于不拘分布，无法使用常见分布密度曲线拟合频率分布直方图。只能直接采用分位数法确定阈值。将97.72%、99.87%分位数设为预警阈值和报警阈值，对应数值分别为0.8 μg/g、1.0 μg/g。

3 讨论分析

各元素阈值见表1。一些从事柴油机油液监测的技术人员在统计经验阈值时，不注重考虑样本分布是否符合正态分布及零散极大值处理，直接通过Xˉ、S确定阈值T1和T2。这一处理方式过于简单，所确定数值与前文所述阈值（见表1 中预警值、报警值）存在较大差异。其中，镁、铝、钠、镍元素的T1 和T2 值，远大于前文确定的预警值和报警值；铁元素T2 值则偏低，明显小于报警值。表1中，T1为Xˉ+ 2S，T2为Xˉ+ 3S。

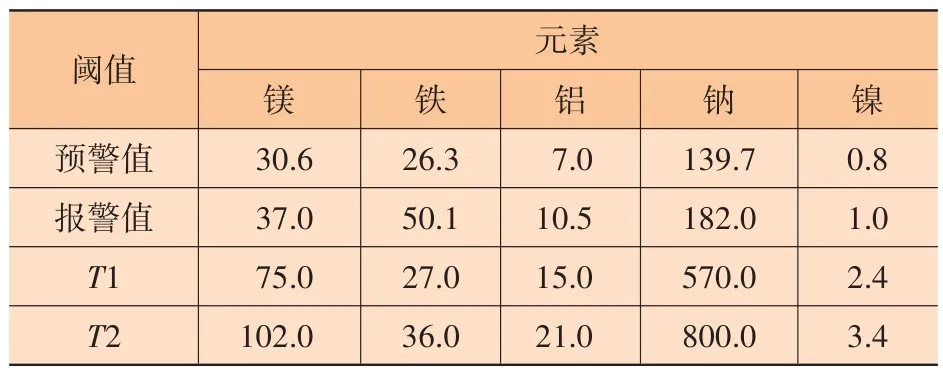
表1 各元素阈值 μg/g

阈值是否合理需通过实践进行分析。一是以故障案例数据为基础的参考分析。例如，我单位监测工作中曾发现润滑油受海水污染案例，其钠、镁元素质量分数分别为240.0 μg/g 和38.1 μg/g，如果用表1 中T1、T2 值作隐患判别，会出现漏报情况。二是关于装备使用及维护保养情况调研分析。例如，对铁元素质量分数位于36.0～50.1 μg/g 之间样本进行调研分析，了解相关船舶取样前后一段时间内装备维护保养情况，并未发现缸套、气阀、传递齿轮等铁元素主要来源部位存在异常问题，说明以铁元素T2 值（36.0 μg/g）作为报警值过于保守。综合以上分析不难看出，直接通过Xˉ与S确定阈值是不合理的。相比较而言，前文所述方法确定的预警值和报警值更符合实际。

理想的阈值应能对故障隐患及时做出报警，避免故障漏报，并尽可能减少虚报问题发生。前文确定的预警值和报警值还只能称为经验阈值，要达到理想阈值标准还有待在后续监测实践中不断检验和修正。

4 结束语

1）该型柴油机光谱分析数据中绝大多数元素原始样本并不符合正态分布，并伴有明显拖尾现象，直接采用传统的三线值方法统计经验阈值是不合理的。

2）应根据样本分布特点选择恰当数据处理方法统计经验阈值。本文对5种典型分布采用了不同数据处理方法，可作为类似问题分析参考。

3）零散极大值数据会使统计的经验阈值过大，分析时有必要对极大值数据做相应筛除。针对不同分布，本文采用的基于Xˉ+ 3S的筛除循环流程和半钟形分布数据筛除循环流程，可获得理想的数据筛选效果。

4）相比传统方法阈值，本文方法确定经验阈值更为合理，但还需在监测实践中不断检验与修正。