阵列射流空间填充水滴形Kagome桁架的靶面冷却性能多目标优化*

2023-11-08冉泓鑫阮麒成高建民李云龙

航空制造技术 2023年19期

徐亮，冉泓鑫，阮麒成，席雷，高建民，李云龙

（西安交通大学，西安 710049）

射流冲击冷却是单相冷却工质下冷却能力最高的冷却方式，工业中广泛地用于燃气轮机中[1]。燃烧室作为燃气轮机的“心脏”，是燃气轮机最重要的部件之一，其工作环境极其恶劣，并且在高温、高压的燃烧火焰及热燃气的共同作用下，火焰筒常常会出现裂纹、翘曲及变形。为了提升燃烧室过渡段的换热性能，阵列冲击射流传热性能一直是传热领域的研究热点[2–4]。于征磊[5]和王辉[6]等在国内首次将冲击冷却技术应用在了火焰筒的过渡段，并进行了相关的设计，研究结果表明，在保证冲击射流孔布置方式不变的情况下，过渡段导流衬在沿冷却工质流动方向上的曲率过大会降低整体的冷却效率。Xu等[7]通过数值模拟的方法改进了燃气轮机过渡段上的冷却方式，并对冲击孔的角度、排列方式及孔径大小进行了研究和优化，给实际生产提供了一定的理论支持和技术参考。Xu等[8–9]通过试验和数值模拟的方法研究了几种不同螺旋喷嘴的结构参数对冲击冷却的流动和换热特性的影响。阵列冲击射流冷却虽然研究文献较多，但它影响换热性能的因素很多，由此受到传热研究者的持续关注。

随着增材制造技术（Additive manufacturing，AM）的进步，燃烧室过渡段的设计和开发产生了重大变革。罗 · 罗公司通过激光直接沉积成型技术（Direct laser deposition，DLD）实现了火焰筒的3D打印；Kornegay等[10]3D打印了一种环装多孔衬套，以此来减弱燃烧的不稳定现象。随着3D打印技术的日趋成熟，2013年Tibbits等[11]通过将随时间变化的形状记忆效应整合到3D打印结构，首次提出4D 打印技术的概念。目前，关于4D打印的研究大多采用了“3D打印+时间”的概念[12–14]。关于4D打印火箭筒的研究还尚属空白。

桁架结构具有较高的孔隙率，已成为公认的最有前景的新一代先进超轻质超强韧结构，是实现结构超轻量化设计的首选结构[15–17]。由于传统加工无法满足所有桁架的成型要求，以前关于桁架流动换热的研究较少；随着AM技术的完善和桁架的制造水平提高，如何将桁架应用于冷却通道已经成为目前的研究热点。Son 等[18]证明了桁架结构具有金属泡沫材料的高孔隙率和高表面积体积比的优点，同时还会产生更低的压降，是航空航天领域的理想选择。Ekade等[19]对于所考虑的雷诺数范围，发现八角点阵桁架表现出比随机金属泡沫更好的流动和传热特性。目前典型的点阵结构包括四面体桁架结构、金字塔桁架结构、Kagome桁架结构及钻石型结构等[20]。

随着众多学者的不断研究，发现Kagome桁架结构具有优异的机械力学性能和较好的换热效果，在冷却结构的设计中更具有应用潜力。Hyun等[21]通过数值分析的方法对Kagome结构进行了力学分析，发现Kagome桁架结构具有比四面体桁架结构更出色的力学性能。Rakow等[22]研究了Kagome阵列夹芯结构在压缩、弯曲及剪切情况下的力学性能，研究发现Kagome桁架结构较四面体和金字塔桁架结构具有更好的机械强度。Lim等[23]研究发现，Kagome的力学破坏形式为杆件屈曲，并且比四面体结构具有更好的吸能效果。Ullah等[24]研究发现，3D打印的Kagome点阵夹芯结构具有比传统芯材结构更好的力学表现，而且具有极为优异的吸能特性。Gautam等[25]3D打印了丙烯氰Kagome点阵夹芯结构并分析了桁架单元在受到压缩时的性能，此外还研究了杆件方向、直径和表面粗糙度等因素对压缩性能的影响。Krishnan等[26]研究了Kagome、四面体和金字塔3种不同的桁架结构的流动换热特性，结果表明高孔隙率和低流阻是提高综合换热能力的重要因素，并且Kagome桁架结构具有更好的换热能力。Kemerli等[27]研究了恒定热流密度和恒温条件下Kagome支杆长度和直径对共轭强迫对流换热的影响，研究表明，支杆长度减少和支杆直径增加会造成Kagome芯的压降增大；平均传热率和传热速率会随着支柱长度减小而显著增加，支柱直径影响不大。Parbat等[28]研究了嵌入Inconel 718 Kagome晶格的微通道的热性能，结果表明，相对于光滑通道，Kagome桁架产生了3～6倍的传热增强。在射流空间内部置入Kagome桁架结构，能利用其复杂的多支桁架来增强换热。Kagome桁架结构因具有优异的力学性能和高效的换热能力，有望成为4D打印下燃烧室过渡段的主要扰流结构。

但是另一方面Kagome桁架结构也存在流阻大的缺点。不同肋柱扰流器的截面形状对流动和换热特性的影响也不尽相同，目前针对肋柱扰流器的减阻的截面形状大致有水滴形、圆形和新月形。Zhou等[29]通过试验和数值模拟研究了4种减阻结构在Re=21000时的传热性能，这4种结构为方形、三角形、圆形和水滴形；研究表明水滴形结构具有最好的传热性能。Xie等[30]发现水滴形凸起在矩阵通道中有良好的换热性能且流阻较球形凸起小。Rao等[31]通过分析试验和模拟结果，比较了球形阵列凹陷和水滴形阵列的凹陷壁在通道中的传热，发现水滴形阵列的换热性能比球形阵列凹陷高18%。Xie等[32]研究了通道中新月形肋对流动传热的影响。Perwez等[33]对球形和倾斜的水滴形凹陷进行试验和数值研究，发现水滴形凹陷较球形凹陷的传热性能高17%，摩擦系数增加5.93%～16.14%。从上述文献能看出水滴形截面的扰流器有着不俗的潜力，其传热性能较其他截面更好，减阻能力较圆形截面各有优劣；水滴形截面的研究对象主要集中于肋柱和凹陷，目前还没有针对桁架截面的研究。

本文借鉴这种水滴型截面减阻方式，创新性地提出水滴形Kagome桁架结构，并将其作为扰流器运用于阵列射流冲击中。通过简化试验验证数值模拟方法。随后通过数值模拟计算方法改变水滴形杆的直径、截面角和倾角，研究这些结构参数对靶面换热特性的影响。基于计算数据，采用多目标优化的方法拟合了靶面努塞尔数和压损的关联式，并计算出在该结构参数范围下的最优结构，以便对这种新型的4D打印复合冷却结构设计提供一定的参考。

1 试验系统及方法

1.1 物理模型

图1（a）为增材制造燃烧室过渡段核心换热区域的阵列射流冲击原始结构。模型包括入口、出口和试验段3部分，各部分尺寸已在图1（a）中标注。模型入口和出口足够长，以确保流体充分发展，降低入口效应的影响。试验段部分包括冲击孔和冲击区域两个结构。入口稳定段为200 mm×240 mm×260 mm，出口稳定段为18 mm×200 mm×200 mm。冲击孔深度为5 mm，孔径D为10 mm，6×5阵列排布。冲击区域尺寸为18 mm×200 mm×240 mm。材料均为不锈钢。热源为试验段底部恒定的热流密度q。

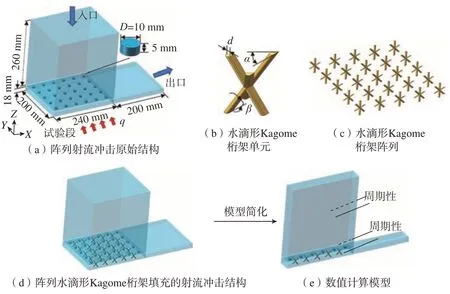
图1 阵列射流空间填充水滴形Kagome桁架结构的物理模型Fig.1 Physical model of the array jet space filled with the teardrop-shaped Kagome truss structure

原始结构冲击靶面采用不锈钢，在使用过程中该靶面经常受热翘曲，引起周围焊缝漏气。本文为了加强靶面的强度，提出Kagome桁架单元作为扰流器，一方面利用其复杂的多支桁架来增强换热，另一方面来增强换热设备的力学性能。为了减小该结构的流阻，采用水滴形Kagome桁架单元。图1（b）和（c）是水滴形Kagome桁架单元及阵列示意图。与传统的Kagome结构类似，该桁架均是由3根杆相接构成，杆之间的夹角固定为120°，桁架的高度为18 mm，与冲击区域的高度保持一致，材料为不锈钢。水滴形截面圆弧直径为d，尾角夹角为α，杆与地面的倾角固定为β。将桁架填充至原始模型后，阵列水滴形Kagome桁架填充之后的射流冲击结构如图1（d）所示。为了简化模型，考虑到阵列排布的桁架结构具有周期性，本文数值模拟的计算模型如图1（e）所示。

桁架单元结构参数和工况参数具体如下：结构参数d范围1～3 mm、α范围45°～90°、β范围40°～50°；优化工况参数q=6000 W/m2，Re=50000。由于实际增材制造精度有限，在制造过程中d=1 mm和2 mm的水滴形Kagome桁架结构无法满足α的成型精度；而α=60°和90°时，桁架截面较小，金属材料容易脱落；β=45°的桁架最易制造。因此试验验证部分只研究d=3 mm，α=45°，β=45°的水滴形Kagome桁架结构在q=2000 W/m2，Re=5000～50000条件下试验数据与模拟数据的对比。

1.2 试验装置

1.2.1 试验系统

试验系统整体示意图如图2（a）所示，主要包括空压机、储气罐、干燥器、多种阀门、流量计、入口整流段、试验段、出口稳定段、测量系统及出口处的消音装置。在本试验中，气体从空压机进入储气罐，通过干燥器干燥后进入管道，流经止回阀、旋拧阀和流量计后进入入口整流段进行整流，稳定后的气体冲击试验段后，通过出口整流段止回阀和旋拧阀排入消音装置降噪，最后排放到大气中。在试验系统中，测量系统负责测量试验段前后的压力、温度及试验板靶面的温度等试验数据。管道内的压力和气量大小可以通过调节旋拧阀来实现。为了降低热量损失，保证试验结果的可靠性，底板外表面还包裹有保温棉。整个试验系统通过螺栓紧固件连接。图2（b）和（c）为试验段的具体结构。加热采用薄膜加热器来实现，为了保证加热的均匀性，在加热膜与试验板之间增加一层紫铜板。底板结构为隔热材料，并能起到密封作用。试验板的外表面焊接有热电偶，并从紫铜板和加热膜上提前布置好的直径为2 mm的圆孔中引出。

图2 试验系统Fig.2 Test system

1.2.2 试验件及温度测点分布

图3（a）和（b）为水滴形Kagome桁架阵列的示意图及实物图。桁架结构通过卡夫特K–5204K导热硅胶粘接在试验板上，可以手动调节排布方式，以及更换桁架扰流结构。该导热硅胶导热系数为1.6 W/（m·K），耐温峰值为250 ℃。在试验件的背面布置有11个热电偶测点，测点间的距离为20 mm，其具体排布形式如图3（c）所示。为方便后续分析，以向右为x方向的正方向，以中心点为坐标原点0，坐标值用x/D表示。紫铜板厚2 mm，一面紧贴加热膜，一面紧贴在试验件的外侧，保证试验件加热均匀，其表面设有直径2 mm的圆孔，方便热电偶引出，如图3（d）所示。薄膜加热器为定制的聚酰亚胺薄膜加热器，为方便热电偶穿过同样面上打孔，尺寸为240 mm×200 mm×0.1 mm，通过两根导线接直流电源工作，可根据电源的电流电压来实现加热功率的调节，进而调整热流密度，如图3（e）所示。底板为橡塑材料，导热系数为0.02 W/（m·K），基本可以认为绝热，通过螺栓与腔体连接，起到密封和隔热作用，接触面上同样打孔，热电偶从中穿过，一端焊接在试验板外表面，一端从孔中引出接入采集系统，如图3（f）所示。

1.2.3 测试内容和仪器

测量数据包括流量数据、温度数据和压力数据3部分。

流量测量是测量入口冷却气体的流量，可以通过改变流量的大小来研究雷诺数对试验结果的影响。试验中使用涡街流量计来直接读取入口处的冷却气体的流量。

温度测量包括入口气流的温度和试验板冲击靶面的温度。入口气流的温度测量采用插入式的K型热电偶，该热电偶测温范围为0～1000℃，误差为±2.5 ℃，直径为5 mm，输出4～20 mA电流信号；试验板冲击靶面的温度测量采用焊接式的E型热电偶，该热电偶测温范围为0～400℃，误差为±2.5 ℃，同样输出4～20 mA电流信号。使用热电偶标定炉JUPITER650对两种热电偶标定，标定后它们在30～150 ℃的范围内误差不超过1.2 ℃（精度达1%左右）。

压力测量是测量入口和出口的压力，通过两者压差来计算流动损失，继而研究不同桁架结构对流阻的影响。试验段前后的压力通过压力变送器直接读取，该压力变送器采用12 V直流电源供电，精度为0.075% FS。

1.2.4 数据处理

单个射流孔的横截面积Aj定义为

式中，D为冲击孔的直径，m。

雷诺数Re定义为

式中，mj为单个射流孔的质量流量，kg/s；μ为冷却空气动力黏度，kg/（m·s）。

努塞尔数Nu和平均努塞尔数Nuave用于评估传热。其公式定义为

式中，h为对流换热系数，W/（m2·K）；λ为流体导热系数，W/（m·K）；q为靶面加热热流密度，W/m2；Th为靶面温度，K；Tg为冷却气体温度，K。

压损系数Cp用于评估流阻，定义为

式中，ΔP为进、出口静压压差，Pa；ρout为出口气体密度，kg/m3；uout为出口速度，m/s；W为出口宽度，m；H为出口高度，m；Pout为出口压力，Pa；mout为通过出口的质量流量，kg/s；Tout为出口静温，K。

综合影响因子F用来评估综合换热性能，定义为

式中，Nu0为未置入桁架的阵列射流冲击模型的平均努塞尔数；Cp0为未置入桁架的阵列射流冲击模型的压损系数。

1.2.5 不确定度分析

由于数据在试验时与真实数据之间存在一定的误差，因此为了保证试验数据的可靠性，需要对试验数据进行不确定度分析。已知试验的参数、示值及标准不确定度分量如表1所示。

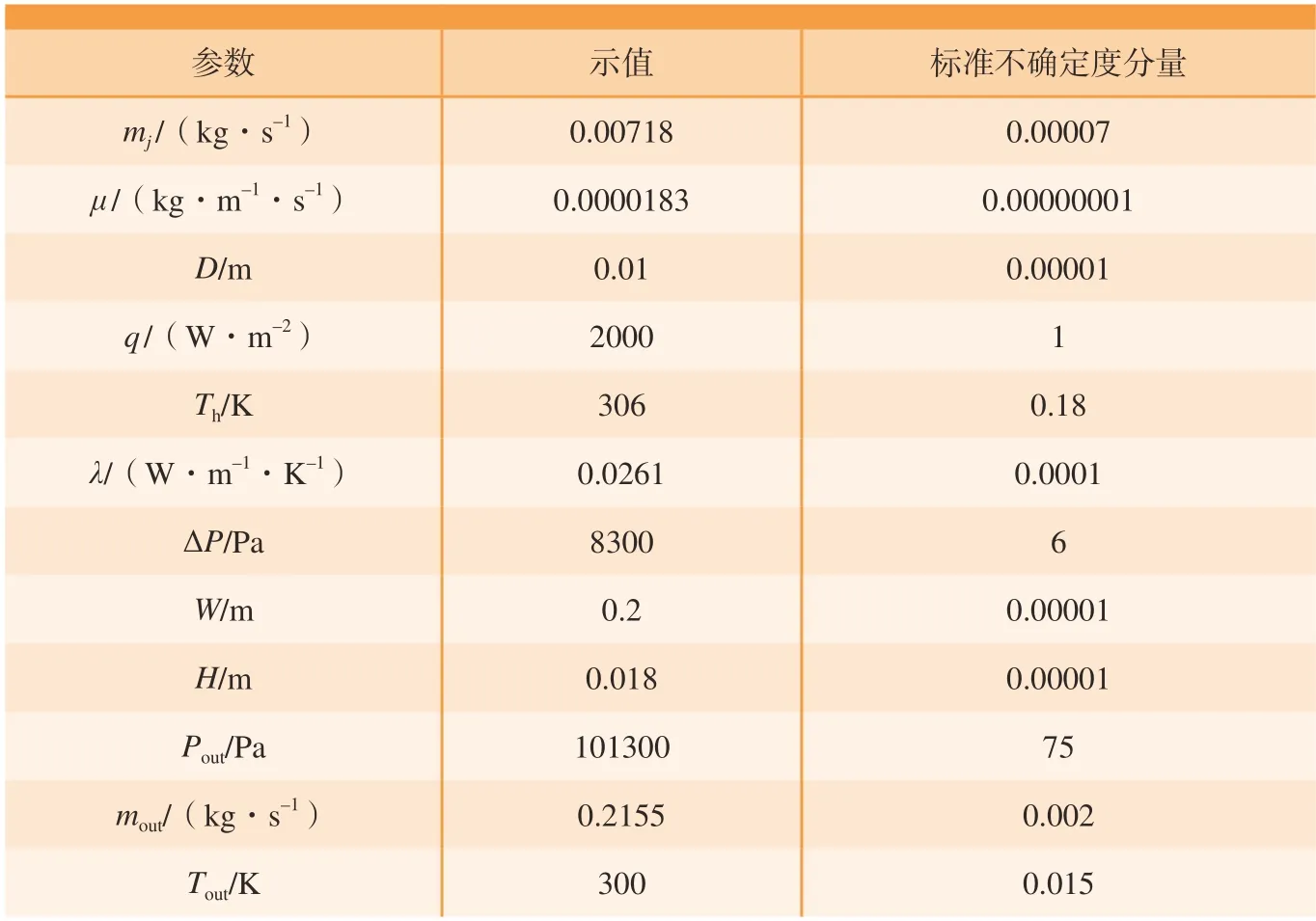
表1 试验参数、示值及标准不确定度分量Table 1 Test parameters,indication values,and standard uncertainty components

Re标准不确定度合成公式为

Nu标准不确定度合成公式为

Cp标准不确定度合成公式为

经过计算，试验测量的Re、Nu和Cp的合成标准不确定度分别为561、3.87和0.102。取包含因子k=3，最终计算得Re、Nu和Cp的扩展不确定度为1683（3.36%）、11.61（9.08%）和0.306（5.59%）皆小于10%，可以认为本试验测量结果是可靠的。

1.3 气热耦合数值计算方法

1.3.1 计算域网格及其边界条件

采用Workbench 18.0的Meshing模块进行非结构网格划分。由于模型较为复杂，本文在网格划分过程中为了兼顾网格质量和计算速度，采用了移动周期性边界，使得计算结果更加贴近实际工程应用，并用Curvature和Promixity方法优化曲面和边缘区域的网，还对流体域近壁面网格进行了加密处理，第一层网格高度0.001 mm，增长因子1.2，保证壁面y+值小于1。具体的网格划分如图4所示（蓝色为流体域，红色为固体域）。采用SSTk–ω模型[9，34]，二阶迎风差分格式，收敛尺度为10–5。数值模型的边界条件如下：射流入口为质量流量入口，质量流量通过式（2）的雷诺数反推；出口为压力出口边界，压力大小为一个大气压。入口气流温度大小恒定300 K，入口湍流度5%。冲击底板下表面施加恒定热流密度边界条件，q=6000 W/m2。侧面施加移动周期性边界条件，流固交界面设置为耦合面，其余壁面绝热无滑移。工质选择理想气体，固体壁面为不锈钢。

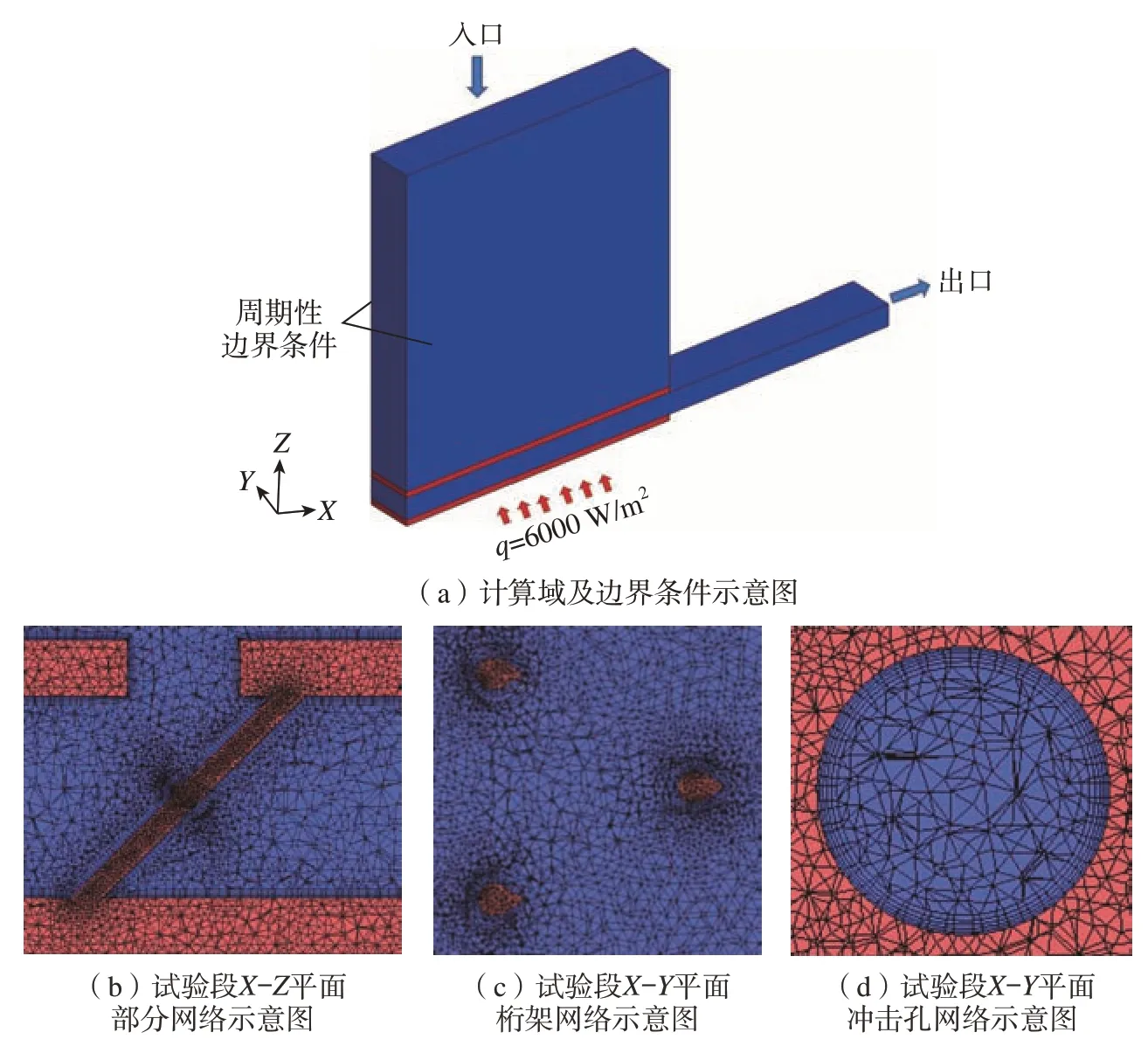
图4 网格及边界条件Fig.4 Grid and boundary conditions

1.3.2 网格无关性验证

图5所示为冲击射流雷诺数Re=30000时，冲击靶面的Nuave随不同网格数的变化折线图，从中可得，随着网格数的增加，Nuave也在不断提高，当网格数增长到420万时，网格数量再继续增长，Nuave的变化不再明显，因此选取网格数量为420万左右。

图5 网格无关性验证Fig.5 Grid independence verification

1.3.3 数值方法的验证

为了验证数值计算方法的可靠性，选用试验数据与数值模拟结果进行对比。试验结构参数和工况为d=3 mm，α=45°，β=45°，q=2000 W/m2，Re=5000～50000。图6（a）是在不同雷诺数下试验数据和模拟数据的Nuave对比图，其最大的差为10.5%。图6（b）是q=2000 W/m2，Re=20000时，试验数据和模拟数据的局部Nu的对比，可以看出两者吻合良好，最大误差为3.8%。

图6 数值计算验证Fig.6 Numerical calculation verification

1.4 基于ISIGHT平台的优化方法

1.4.1 优化流程

使用ISIGHT集成平台，优化流程图如图7所示。首先在DOE模块中通过中心组合设计（Central composite design，CCD）确定d=1～3 mm，α=45°～90°，β=40°～50°，3因素3水平下的试验参数组合；再通过数值计算方法分别计算出各个工况下的Nuave和Cp，以此构建样本集；然后通过建立响应面模型构建满足精度要求（R2>0.900）的近似模型；最后通过第二代非劣排序遗传算法（Nondominated sorting genetic algorithm-II，NSGA-II）算法建立Pareto解集，用优劣解距离法（Technique for order preference by similarity to an ideal solution，TOPSIS）搜索最优解，并与最优解对应结构参数的计算结果对比。其中NSGA-II算法中种群大小为20；遗传代数为100；交叉概率为0.9；交叉分布指数为10；突变分布指数为20。

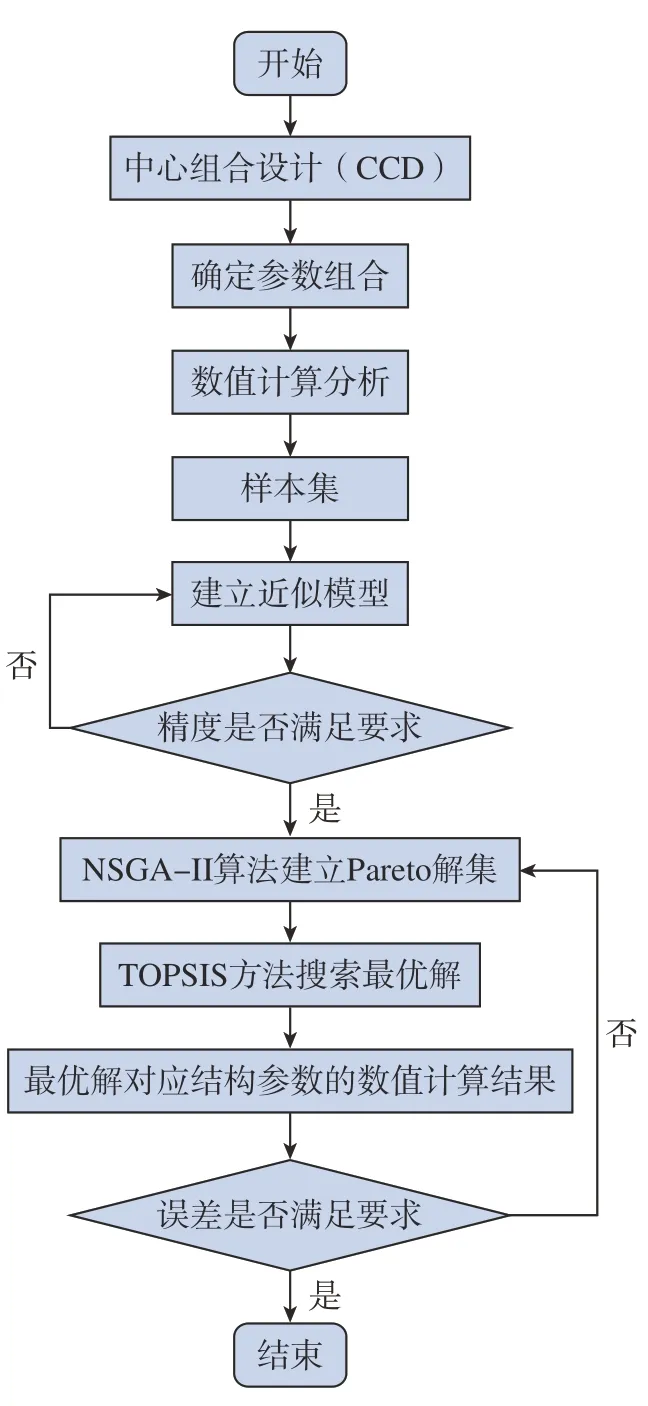
图7 优化流程图Fig.7 Optimization flow chart

1.4.2 优化方程及其拟合精度评价指标

设计变量为x1、x2、x3，设计变量与结构参数的关系为

目标函数为

多目标优化的数学模型为

响应平均值与响应估计值差的平方和计算公式为

响应实际值与响应平均值差的平方和计算公式为

式中，yi为响应实际值。

误差的离均差平方和公式为

f值计算公式为

2 结果与讨论

2.1 响应面模型下计算样本分析

基于CCD获得的研究参数排列及计算结果如表2所示，其中响应值由CFX数值模拟得到。输入参数包括d、α、β，响应值包括Nuave和Cp。3个输入参数分别为低、中、高值，因此本文对中心复合设计共安排了20个数值模拟案例，排列顺序随机生成。

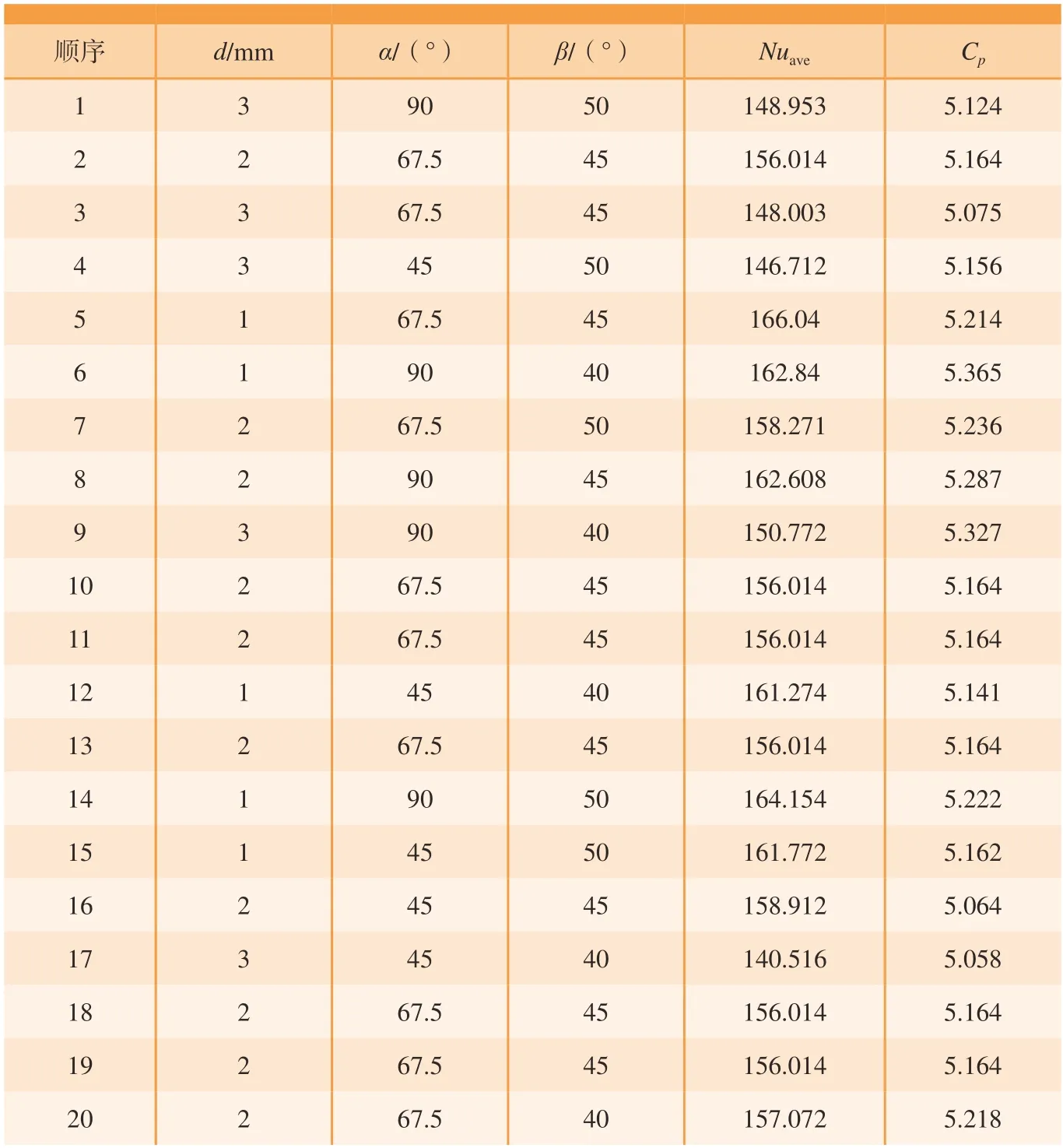
表2 研究参数布置及计算结果Table 2 Arrangement of research parameters and calculation results

拟合相关系数如表3所示。由表2可以看出，研究参数总共3个，因此通过试验设计和响应面法拟合得到的经验公式中有10个系数，其中1个实项、3个线性项、3个平方项和3个交互项。

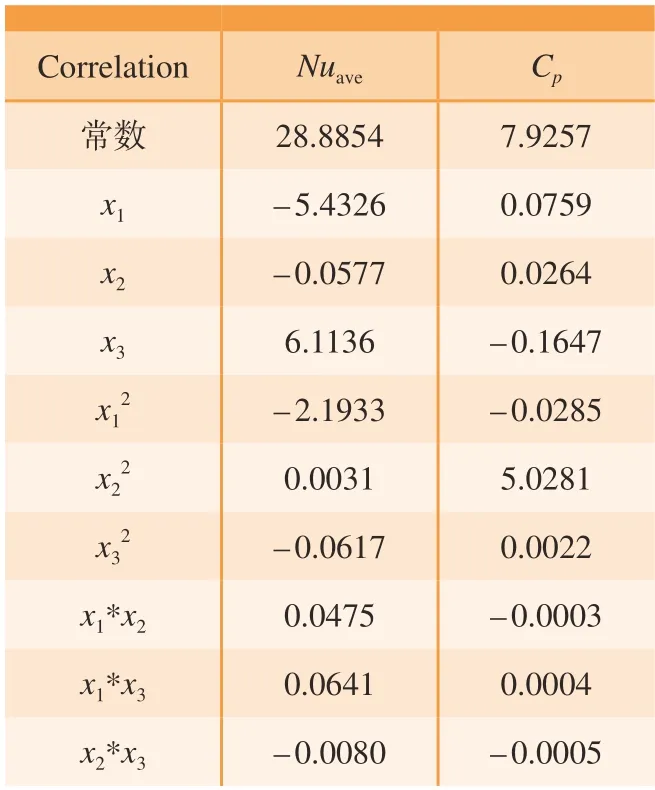
表3 拟合相关系数Table 3 Fitting correlation coefficient

表4和5分别为Nuave和Cp的方差分析表。其中，模型自由度等于变量个数，从表4中可以看出，有3个线性变量、3个平方变量和3个交互变量，共9个变量；总自由度为模拟案例个数减1；误差自由度为总误差减模型自由度。在方差分析中，研究参数的较大波动表明对响应的影响显著。AdjSS为调整后方差平方和，反映了数据波动的大小。AdjMS为调整后均方差，即AdjMS根据数据个数进行的修正，AdjMS=（AdjSS/自由度）。f值和p值是用于假设检验的方差分析中的统计量。f值越大，表示这一项越重要。当p值小于0.05时，表示该项对模型显著；当P值大于0.05时，意味着该项可以忽略不计。从表4中可以看出Nuave对d和α变化较为敏感，Cp对d、α、β2和α*β变化较为敏感。

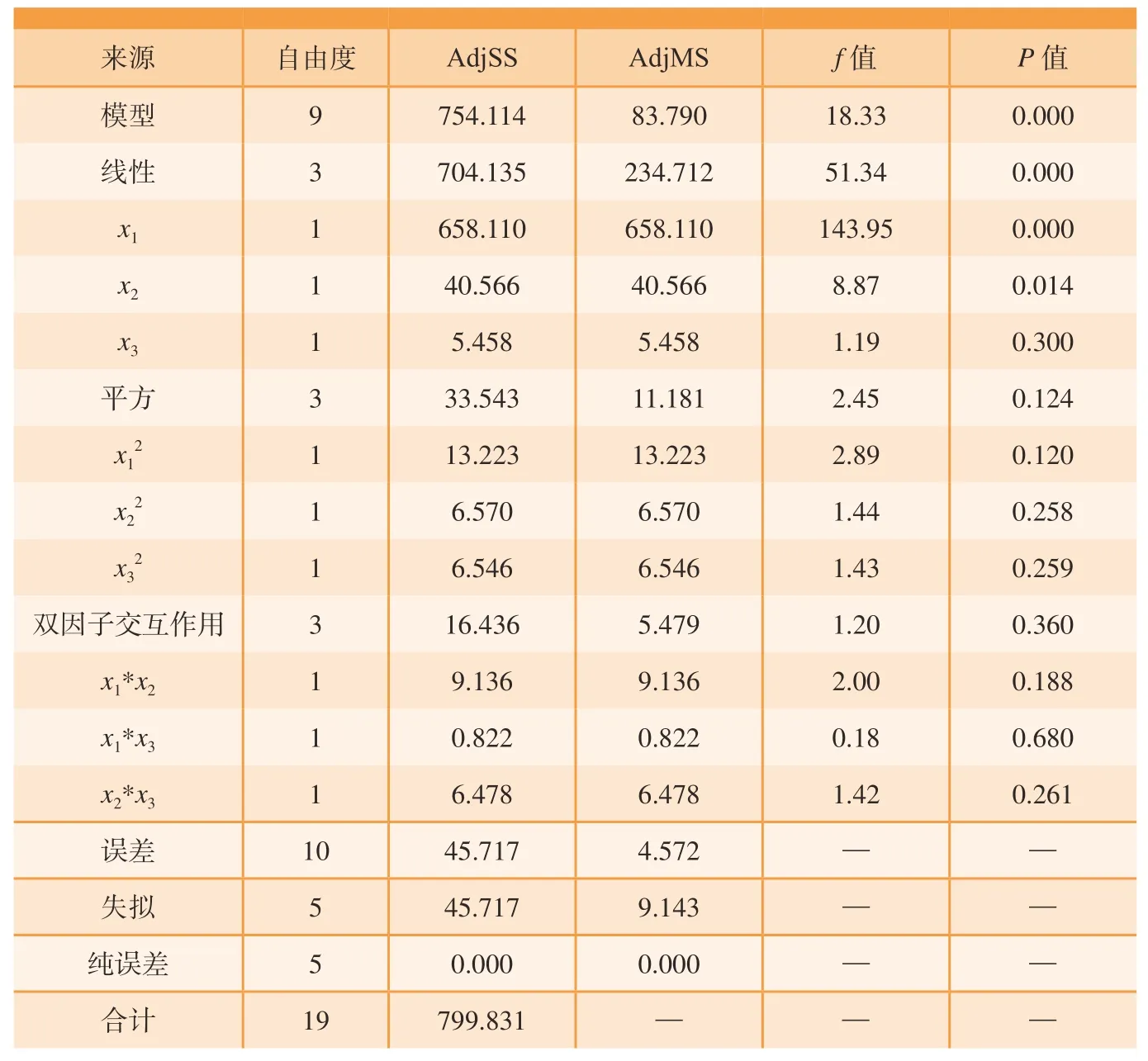
表4 Nuave方差分析表Table 4 Variance analysis of Nuave

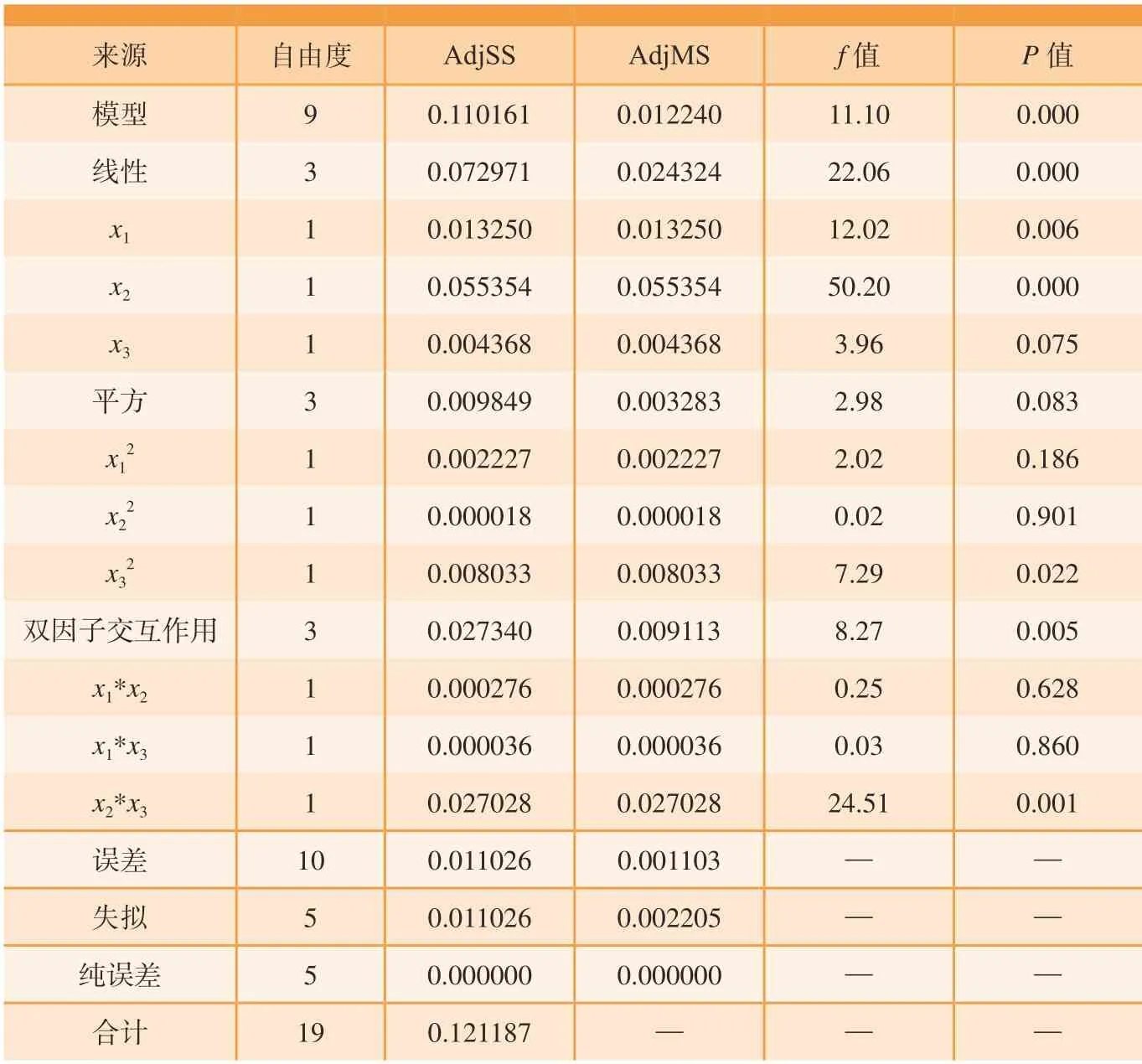
表5 Cp方差分析表Table 5 Variance analysis of Cp

图8给出了Nuave和Cp的响应面模型模拟值和预测值的对比。其中黑色实线为数值计算值，红色散点为响应面模型预测值，蓝色线为数值计算值的±5%误差线。由图8可以看出，Nuave和Cp的预测值均在±5%误差线以内，最大误差分别为1.70%和0.80%，平均误差分别为0.89%和0.38%。Nuave和Cp的经验公式的相关系数R2分别为94.28%和90.90%，均大于90%。上述结果表明，本文拟合的二阶响应面模型可用于预测水滴形Kagome桁架结构的靶面努塞尔数和压损，为水滴形Kagome桁架结构的优化设计提供了精确的近似模型。

图8 Nuave和Cp模拟值和预测值的对比Fig.8 Comparisons of simulation results and predicted results of Nuave and Cp

2.2 第二代遗传算法优化结果分析

根据1.4节中NSGA-II算法的参数设定，计算的所有解如图9中黑色圈所示。Pareto解集是一系列非劣解，如图9中红色圈所示。TOPSIS方法是一种通过计算可行方案与理想解的接近程度的评价方法，广泛应用于多目标决策分析，以式（17）和（18）赋予Nuave和Cp权重，通过计算所有Pareto解集的评价标准S，选取S最大值为TOPSIS最优解，如图9中蓝色圈所示。

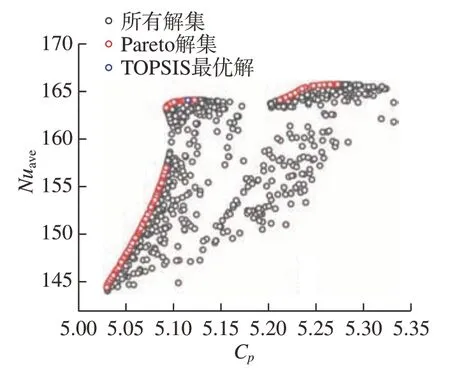
图9 优化结果分析Fig.9 Analysis of optimization results

在Re=50000，q=6000 W/m2时，优化目标为Nuave最大和Cp最小的情况下，TOPSIS最优解对应的结构参数为d=1.000 mm，α=45.001°，β=46.623°。Nuave、Cp和F的优化结果与模拟结果误差分别为1.24%、0.18%和1.20%，如表6所示。说明此多目标优化方法对于预测水滴形Kagome桁架结构的流动换热特性是可靠的。

2.3 优化件及基础件的流动传热分析

图10为q=6000 W/m2，Re=50000时，试验件（d=3 mm，α=45°，β=45°）和优化件（d=1.000 mm，α=45.001°，β=46.623°）的云图对比。在图10（b）平面1速度及流线云图中，射流孔处及桁架回流区域优化件的速度略大于试验件，试验件的流场中存在更多的回流及不规则的旋涡。在图10（c）平面2速度及流线云图中，沿流向方向随着横流效应的增强，射流速度在逐渐提高，低速区域面积逐渐减小。射流冲击到靶面的射流滞止位置在不断向流向方向移动。射流与横流撞击而形成的旋涡面积沿流向不断减小，并随着横流效应的增强其涡核逐渐被压向壁面。优化件的红色高速区和蓝色低速区皆略多于试验件，产生的旋涡回流更多且更加规则。优化件相比于试验件，Cp减小了0.93%，流阻变化不大。在图10（d）平面3温度云图中，沿流向方向随着横流效应的增强和射流速度的提高，温度越来越高，换热效果越来越差，高换热区域发生在桁架肋柱之间的区域。相同位置上试验件的温度几乎都高于优化件，且优化件的温度均匀性更好。在图10（e）平面3Nu云图中，可以更明显地看出高换热区域在桁架肋柱之间的区域，且优化件在整个靶面上均保持了较好的换热性能，而试验件随着流向方向换热性能减少较大，体现出优化件的换热均匀性更好。优化件相比于试验件，Nu增加了12.78%，F增加了13.13%。