任意基点法坐标转换在工程测量中的应用

林乐胜,卢清超,姚先峰,雷敉达,朱 恒,郭宝宇

(1.江苏建筑职业技术学院 建造学院,江苏 徐州 221116;2.江苏省测绘市场管理中心,南京 210013;3.江苏省测绘地理信息职业技能鉴定指导中心, 南京 210013;4.江苏有线数据网络有限责任公司,南京 210019;5. 南京捷鹰数码测绘有限公司,南京 210019;6.中国矿业大学 环测学院,江苏 徐州 221116)

在工程施工测量或职业、行业技能大赛中,坐标旋转的应用比较常见[1-5],例如,为了方便施工可以将测量坐标转化为当地的施工坐标,使设计图中的建筑物主要轴线平行于施工坐标系,通过简单的坐标值加减就可以解算出两点间距离,既方便计算数据的检核,更可以简单地通过丈量距离,方便进行放样施工[6-11]。而在几十乃至上百支参赛队伍进行的职业技能大赛中,一次上场不过四五支参赛队,为了避免作弊,组织者应该为所有参赛队准备各不相同的数据,但这项工作因场地的因素不可能实现。因此,在同一个比赛场地使用同样的一组控制点,通过坐标旋转生成不同组的坐标来适应多场次、多队伍的竞赛,成为竞赛组织者的必然选择。

1 常用坐标转换方法

工程上采用的坐标系多为直角坐标系,而且在小区域工程中采用平面直角坐标系不需顾及地球曲率,因此进行坐标转换一般采用“三参数”法(两个平移ΔN、ΔE、一个旋转α)进行坐标转换计算[11-15]。

1.1 常用坐标转换公式

此处约定,施工坐标系也是地方独立坐标系,用o-xy表示,测量坐标系也是国家坐标系,用O-NE表示。

当前坐标转换普遍采用如下的“三参数”法转换公式。

1)施工坐标系转测量坐标系原理如图1所示[1]。

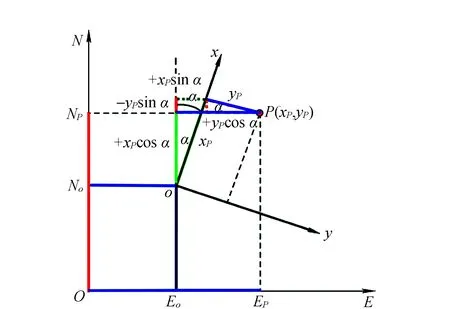
图1 施工坐标系转测量坐标系

由图1中分析可得:

(1)

2)测量坐标系转施工坐标系原理图如图2所示[1]。

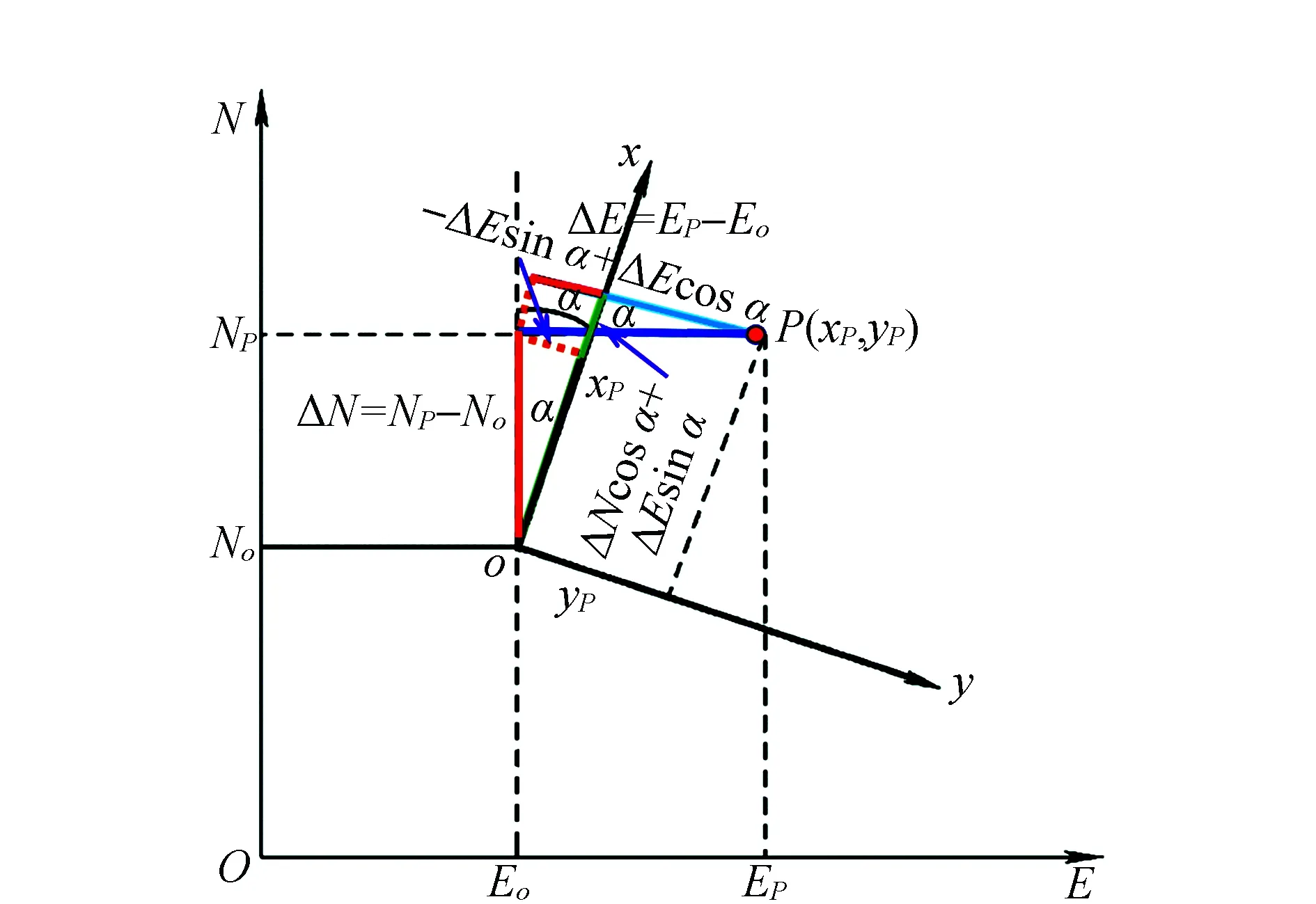
图2 测量坐标系转施工坐标系

由图2中分析可得:

(2)

上述两坐标系互相转换公式中No、Eo分别为坐标原点即N、E坐标平移量。坐标系旋转角度顺时针方向取正值,逆时针方向取负值。

1.2 坐标转换检核方法

为了检核坐标旋转计算的正确性,最方便直观的方法是把原始点位坐标和转换后的坐标导入CAD中,观察所有点的位置变化,如果有点位坐标计算错误,即能一目了然地发现[16],但因为N、E坐标整数都是7～8位,即便旋转的角度很小,旋转后的点位坐标一般都会远离原始点位的位置,如式(1)计算,坐标系旋转5°00′00″,旋转后坐标大约偏离了ΔN=30 km、ΔE=330 km,这样在一幅图中是无法显示旋转前后点位的,不方便观察比对。主要原因是在于坐标的旋转是围绕坐标原点进行的,而不是围绕测区的某一点进行旋转。表1为使用施工旋转测量坐标系公式,计算出转换后的坐标值,由原始坐标1旋转、平移得到坐标2,如图3所示。

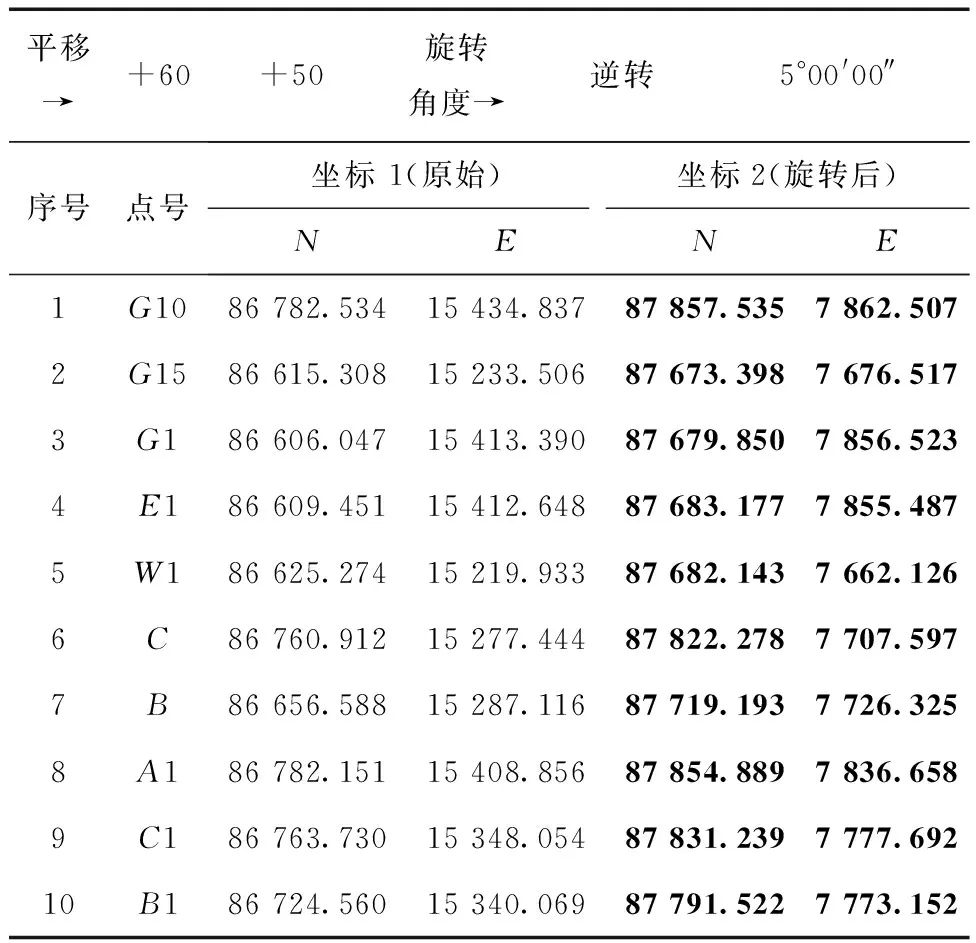
表1 坐标旋转和平移示例

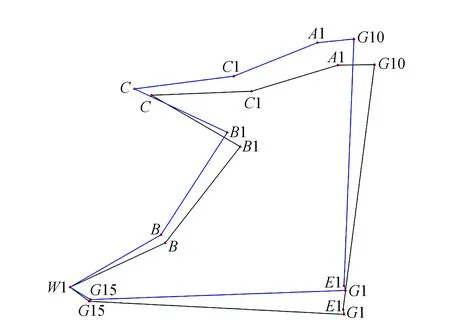
图3 以西南角控制点“W1”为基点坐标系旋转点位移动示例

注:表中坐标数据位数因保密原因有截取。

2 任意基点法坐标转换的定义

3 任意基点法坐标旋转计算示例

为了方便检查坐标旋转之后控制点点位的相对位置及其正确性,以西南角控制点“W1”为基点,将所有坐标点绕此点进行旋转,得到如图3所示的图形,该图精确描述了坐标系旋转后点位的移动情况,旋转计算有无错误一目了然。

具体做法是,先以坐标原点为基点旋转,计算出所有点坐标,再计算出西南角点“W1”原始坐标与新坐标的差值,最后将此差值加到所有点上,即完成了以测区西南角“W1”点为基点的坐标(图形)旋转。

表2为先以坐标原点为基点进行坐标旋转再移动到西南角基点“W1”处的计算结果。

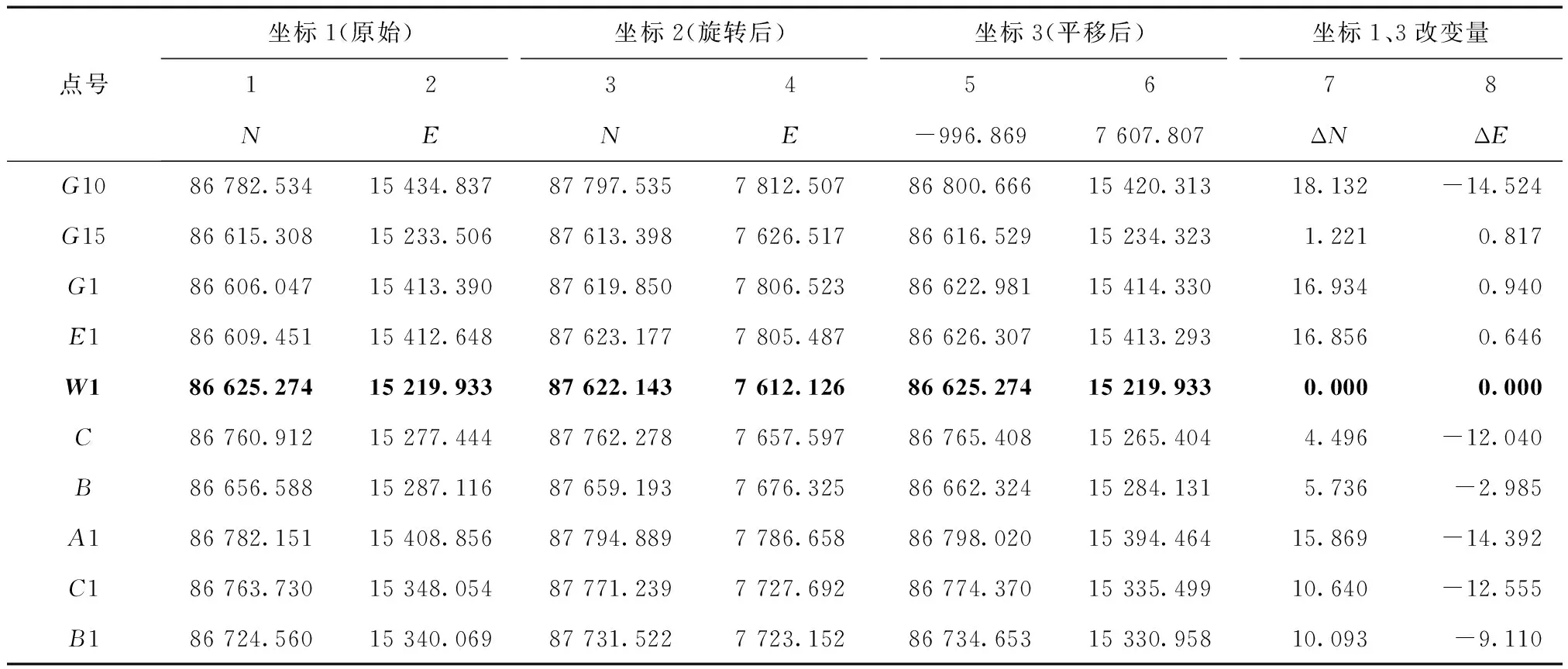
表2 以测区西南角“W1”点为基点旋转的坐标数据

表2中,由10个控制点的坐标1第1、2列逆时针方向旋转5°00′00″得到坐标2第3、4列,再用W1点的坐标1减坐标2得到第5、6列粗黑字体的坐标平移值,然后所有点的坐标2加上坐标平移值得到平移后的第5、6列坐标3,第7、8列为坐标1与旋转平移后坐标3的改变值,表中数据表明以图中任意点做基点旋转,坐标改变值不大,完全可以在同一幅图内直观显示,方便检查除错。

4 任意基点法坐标旋转的工程应用

任意基点法坐标旋转可以应用于建筑工程定位测量和行业测绘技能竞赛中。

4.1 应用示例1

某拟建建筑工程,由0号建筑向北平移4 m成为1号建筑,再由1号建筑向东平移4 m形成2号建筑,依此类推生成其余共10栋建筑,现对该建筑工程进行定位测量。图4表示工程定位图,表3表示各放样点坐标原始及转换后的数据。定位测量须放样建筑物各角点于实地,为了快速、高精度地放样出拟建建筑物各角点坐标,先将图中8、15、42号点放样完成后,然后对拟建建筑各角点坐标进行旋转,再平移到15号点,相当于以15号点为基点进行坐标旋转,此时使用施工坐标,坐标纵轴A平行于15、42两点连线,如此拟建建筑物各角点之间的关系就转化为沿着A、B坐标轴进行的距离丈量,根据15-8、15-42两条主要轴线用“内分点法”量距即可精确确定点位。此法仅需加减运算确定轴线间距就可以定位角点,速度快、效率高,点位越多效果越明显,同时也方便放样质量的检核验收。

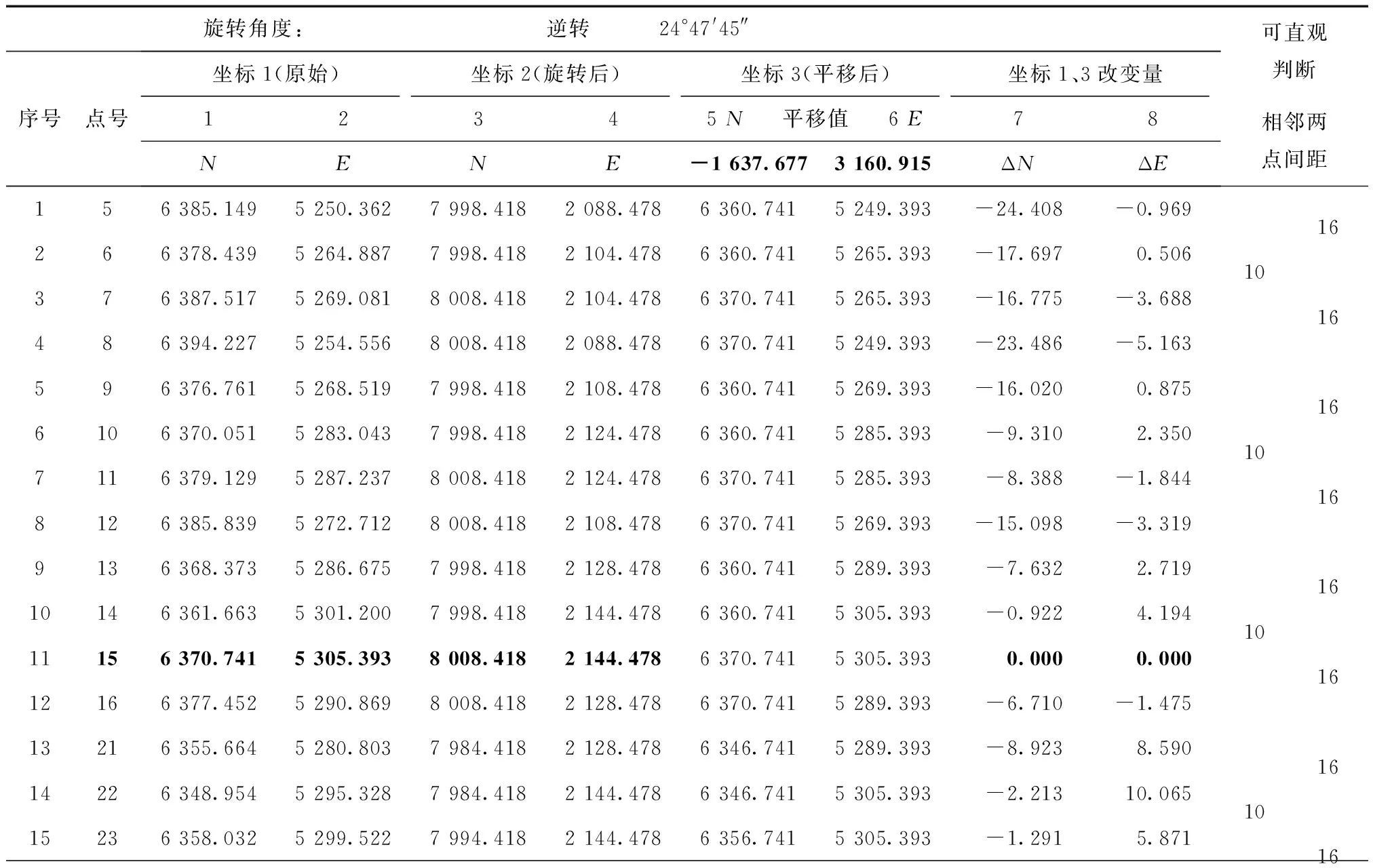
表3 建筑工程各角点坐标旋转平移示例

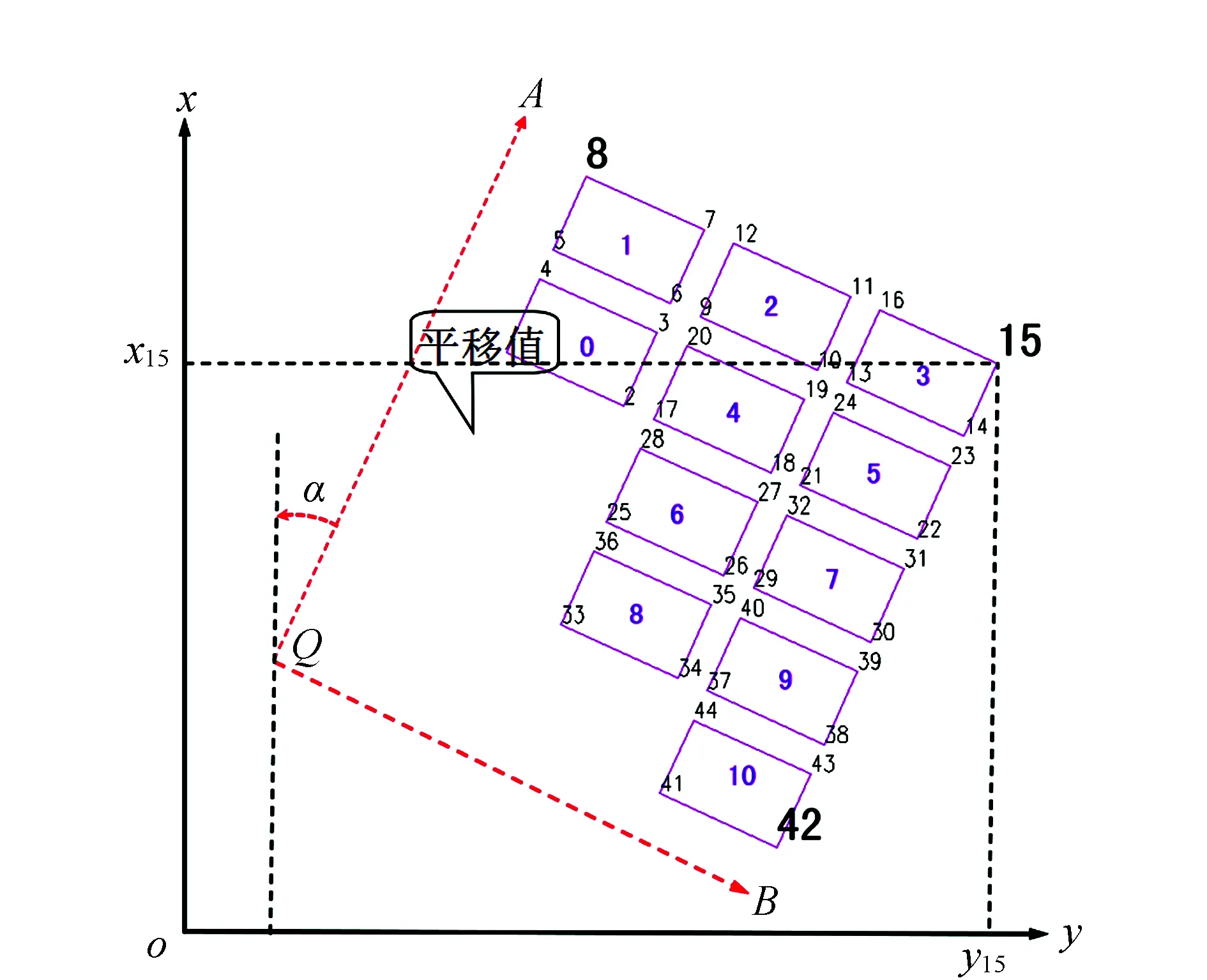
图4 测量坐标系中拟建建筑示例

操作步骤:

1)旋转坐标系:首先反算42至15的坐标方位角,计算出测量坐标系转为施工坐标系需旋转的角度,本例须逆转α =24°47′45.00″,以此计算出旋转后的建筑物各角点坐标。

2)将拟建建筑平移到15号点:如图5所示,计算出15号点原始坐标与新坐标的差值,将此差值加到所有点上,即完成了以15号点为基点的(图形)坐标旋转。

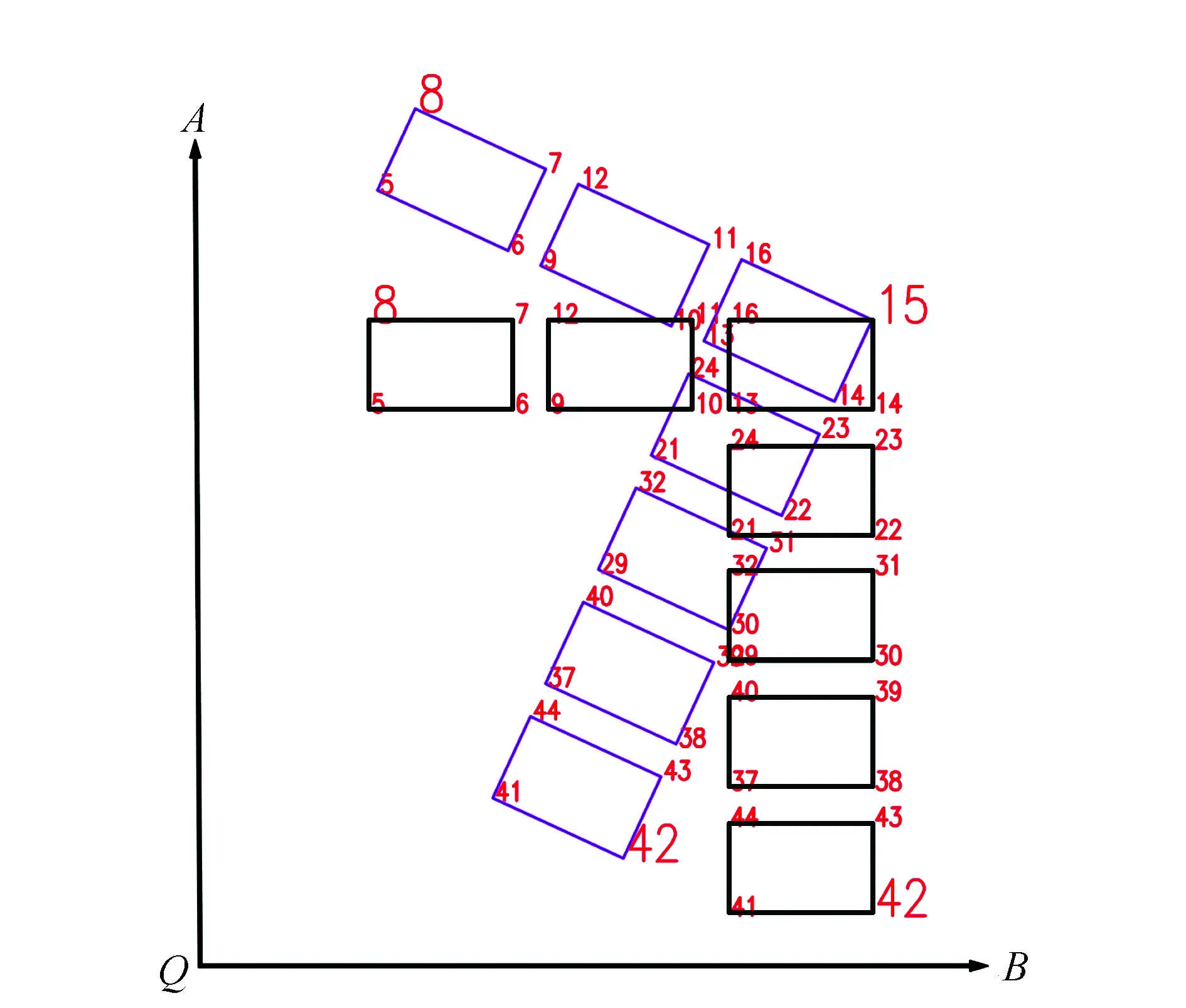
图5 测量坐标系转施工坐标系示例

3)如表3所示,旋转后的图形与坐标轴平行,可直观算出两点间间距,通过在已放样的15-8、15-42两条主要轴线,用“内分点法”仅量距即可精确确定其他各角点点位。

此方法目前已在各类建设工程生产中得到广泛应用,效果良好。

注:先将原始坐标1旋转得到坐标2,再整体平移到15号点得到最终坐标3。

4.2 应用示例2

某省测绘行业技能大赛,数字测图项目,如表4中“坐标1(原始)”所示,原测图区域图走向方向与图廓有一个夹角,且整个图幅偏离图框中心,不考虑实地真实坐标,为了使测图区域位于图幅正中,经坐标旋转、平移后实现,操作步骤如下:

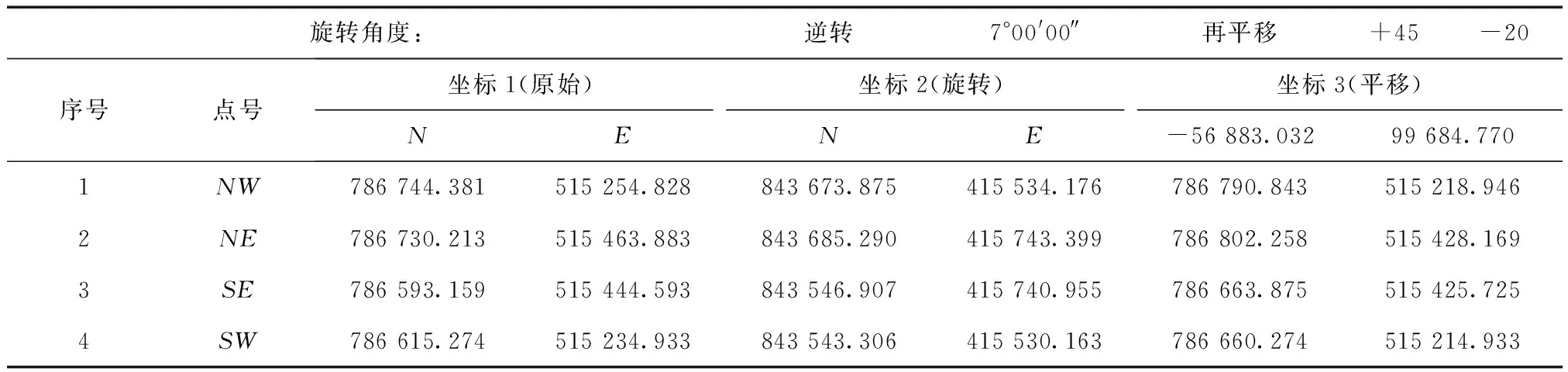
表4 测图边界经旋转后平移后数据

1)如图6所示,首先将测图原始边界点展绘在CAD绘图区,并按照任意图幅绘制图框,以确认测图区域是否偏离图框,本例测图区域边界南北走向向东偏7°的角度,而且东边界偏出的图廓以外,需要旋转及平移。

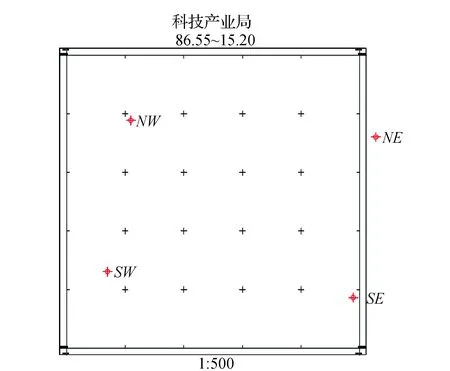
图6 测图原始边界示例

2)如表4所示,以坐标原点为基点旋转,然后平移到SW点,最后再整体再向西北NW方向平移45 m、20 m。得到图7,即测图区域位于图幅正中的坐标。

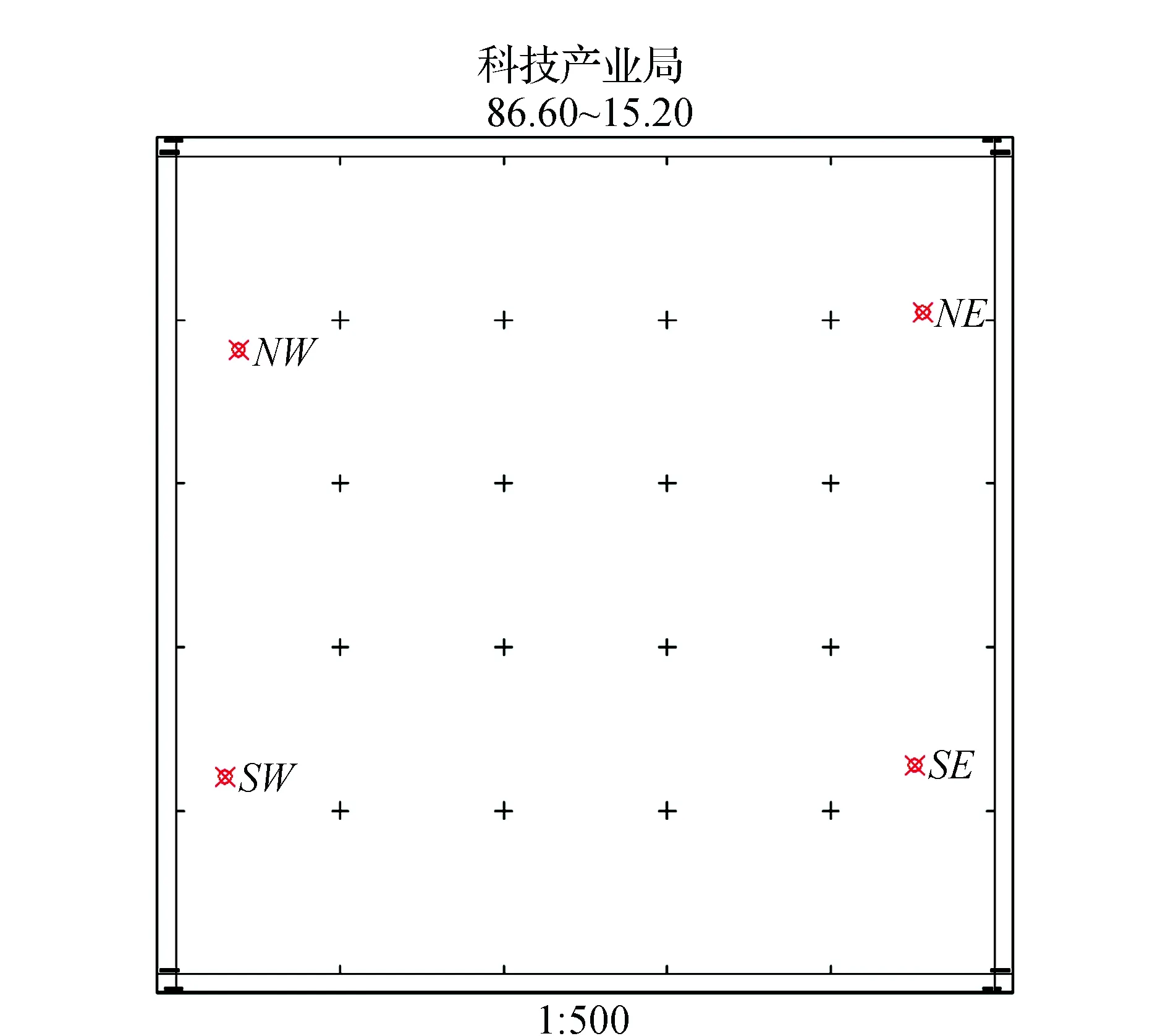
图7 经旋转平移后居图廓正中的测图区域

3)为了防止前面已完成比赛队伍泄露数据,用同样的方法多准备几组数据,为后续参赛队伍提供完全不同数据。如此,既做到了公平公正,又对数据起到了严格的加密作用。

此方法目前已在江苏省各类技能竞赛中得到广泛应用,效果良好。

5 结 论

针对工程测量或行业测量技能竞赛中常用的坐标转换问题,本文提出了一种任意基点法坐标转换方法,主要结论如下:

1)该方法具有严密的数学基础。其实质是以任意一个坐标点为基点进行平移和旋转,改变了原来的以坐标系原点为基点的变换方法,可以确保变换点和原始点落在同一图幅内,从而方便变换检核。

2)经该方法变换后的点与原始坐标点具有非线性关系,而不是简单的线性增减,从而确保了数据的保密性,并防止通过获取已赛队伍数据而作弊的可能性,方便用于行业测绘技能竞赛。

3)该方法计算过程简单、直观,变换成果检核快速,可以大大提高工作效率。

本方法理论基础严密,计算过程简单,可以有效应用于建筑施工放样、区域规划设计,尤其是测绘行业技能竞赛等方面。后续研究将开发基于该方法的可视化手机、平板等APP软件系统,方便对成果进行系统化的管理和应用。