基于特征约束的四面体剖分方法研究

胡长涛,张志华,吴智慧

(1. 兰州交通大学 测绘与地理信息学院,兰州 730070;2. 地理国情监测技术应用国家地方联合工程研究中心,兰州 730070;3. 甘肃省地理国情监测工程实验室,兰州 730070)

随着三维GIS发展及地下工程的需要,地质模型的构建、可视化分析成为地学领域研究热点[1-3]。三维地质建模是基于现代空间信息理论利用地质调查数据实现地质信息的管理、解译、空间分析及可视化,可直观展现地层厚度、岩性及空间形态等属性[4-5]。高质量的地质模型可有效进行地学空间分析与数值计算,为资源勘探及城市地下空间规划提供可靠数据支撑[6]。

空间体元模型作为三维地质模型可视化的基础,在地质资源表达评估及后续定量分析中起着至关重要作用[7]。近年来三维地质建模的方法主要有基于面模型、基于体模型和基于混合模型3大类建模体系[8]。基于面元模型建模方法便于数据更新及可视化,但缺乏内部属性的表达,无法进行空间查询分析。混合模型体拓扑关系复杂,技术实现难度大,当前建模方法研究多以不规则体元模型为主。用于地质建模方面的常见不规则体元有广义三棱柱、六面体和四面体等[9-10]。相比于其它不规则体元,四面体具有体元结构简单、快速几何变换、拓扑关系清晰的优点,可以模拟规则与不规则地质体[11]。地质模型以四面体为基本体元,可实现不规则复杂曲面地质体模型的构建。

Delaunay三角剖分具有严密的理论基础和数学特性[12],限定条件下的三维剖分研究比较成熟,但针对地学领域复杂的边界面及内部特征约束较多的地理空间对象方面的研究较少。因此,文中提出一种基于地质钻孔数据,以地层边界面不规则三角网(triangulate irregular network, TIN)为约束条件,对其进行四面体剖分的模型构建方法。该方法得到可视化效果良好的地质模型,可快速实现三维剖面模型及矿体产量估算等空间分析操作,为地下岩矿体开采等施工提供决策数据支撑。

1 建模方法与流程

考虑Delaunay三角剖分的优良边界约束特性,文中利用克里金插值法生成虚拟钻孔数据并建立地层表面模型。地层侧面利用最短对角线法构建侧边三角网,地层面三角网与侧面三角网构成多地层表面模型。以地层表面模型转换为分段线性复合体作为输入,进行约束四面体剖分得到以四面体为体元的三维地质模型,通过设置不同半径边长比及二面角等特征约束控制格网质量,实现地质模型的更新与重构。模型的基本几何元素有节点、边、三角形面片和简单块体4种。建模过程包括地层表面模型构建、约束四面体剖分两部分,地质模型的可视化借助于VTK(visualization toolkit)组件库实现,技术路线如图1所示。

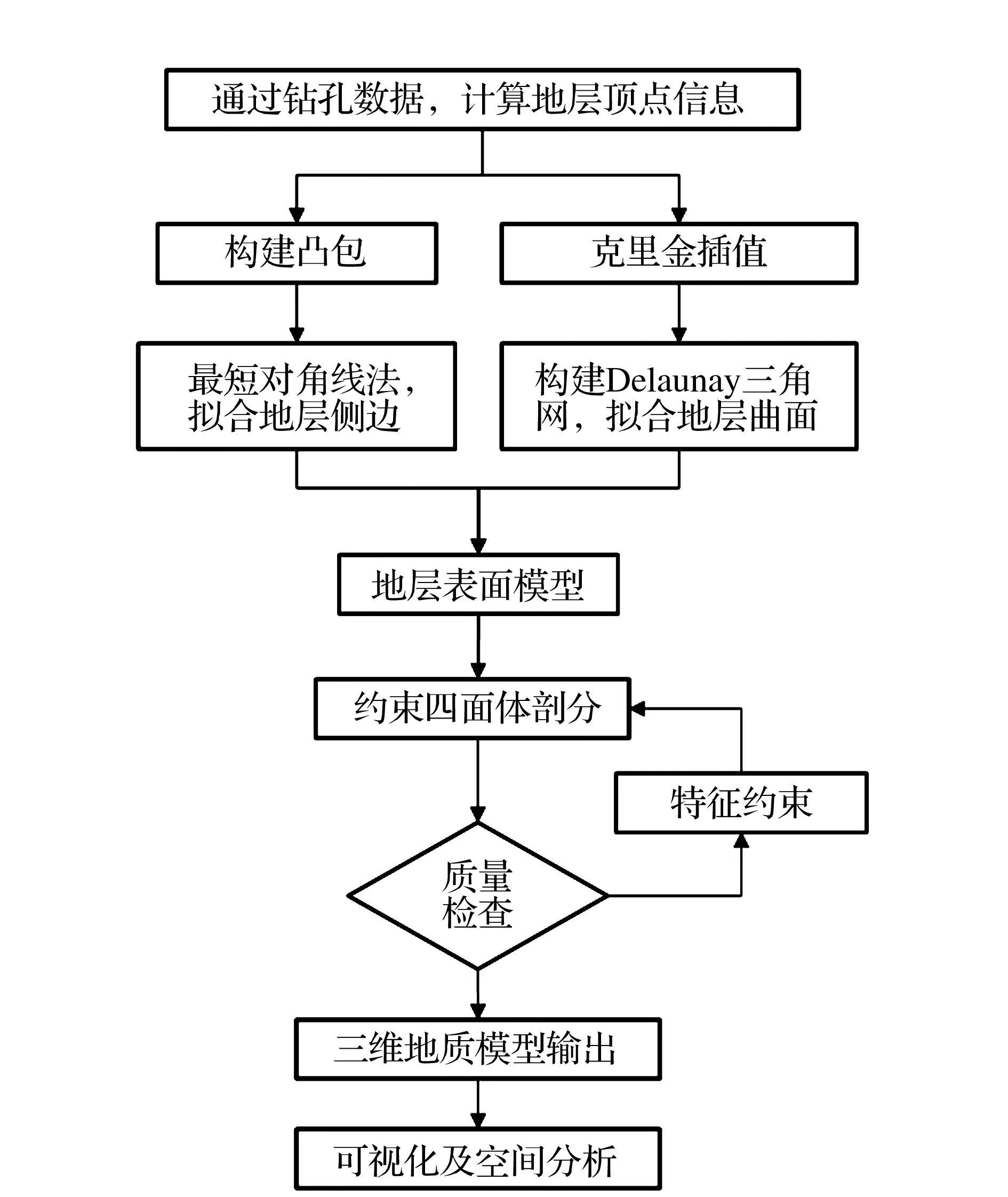
图1 地质建模流程

2 三维地下空间约束表达

地学领域地层的边界面及内部约束特征通常较多,选择适宜的三维空间表达方式有利于构建精确完整的地质模型。文中地质体三维空间的约束表达为分段线性复合体(piecewise linear complex, PLC)。PLC由Miller等[13]提出,三维PLC中X是一个集顶点、边、面和多面体的集合,如图2所示。PLC定义中不允许它的单体非法相交,两个边的相交只能在一个公共的顶点处,并且该点位于X内;四面体T的两个面相交只能是顶点和线段的结合,并且位于X内。另外,PLC允许点、线、面浮动于多面体区域内,在三维表达上灵活,适用于地学建模领域。

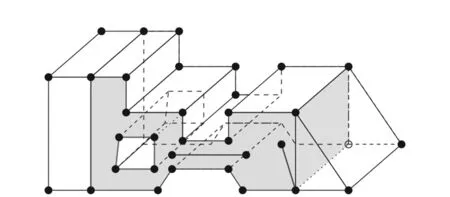
图2 PLC范例

Poly格式文件是PLC的一种线框模型描述,可理解为对分段线性复合体的数字化描述。它由4个部分组成,分别是点列表、面列表、孔洞列表(无空洞即为0)和可选的区域属性列表。在地质建模中,点列表即为地层边界面节点,面列表为三角网的三角面,Poly文件适用于地层约束模型的存储。

3 约束Delaunay四面体剖分算法

TetGen是德国柏林魏尔斯特拉斯应用分析和随机研究所开发的开源高质量的四面体格网生成程序[14]。它可生成精确的约束Delaunay四面体化、边界一致的Delaunay网格和Voronoi分区,可以稳健地处理任意复杂的三维几何形状。

3.1 基于顶点插入的增量Delaunay算法

三维Delaunay剖分算法中使用最广泛的是Bowyer-Watson算法[15],其原理如下:

1)建立一个包含所有点的初始格网,格网通常为点集的最小长方体包围盒;

2)向初始格网中插入点,遍历寻找包含该点的四面体单元;

3)通过邻接关系找出外接球包含的所有四面体单元,删除这些单元构成Delaunay空腔,连接插入点与空腔中的每个顶点生成新的网格单元;

4)重复2)和3)操作直至所有顶点插入完毕,删除格网顶点,得到点集Delaunay四面体格网。

另外,TetGen使用空间排序体制法[16]对插入点进行预排序处理,通过简单的随机行走算法[17]进行点定位,提高了算法的运行速度。通过使用orient 3D(用于点定位)和in sphere(用于更新Delaunay四面体)约束方法保证了算法的健壮性。

3.2 约束Delaunay四面体剖分

约束Delaunay四面体剖分(constrained delaunay tetrahedralization, CDT)由Shewchuk[18]提出,是Delaunay四面体剖分的变体。约束Delaunay四面体化的定义如下:

设X是一个三维PLC,平面f∈X使得P和Q两点位于这个平面的两侧,线段PQ与这个切面相交,PQ两个点也位于X内,但相互不可见。线段不影响可见性,AB是线段,但C和D之间可见。点及平面的空间位置见图3。对于X中顶点形成的四面体PABC,由于它的外接球不包括X中对其可见的点,则四面体PABC为约束Delaunay四面体。其中f相当于约束面。X的四面体剖分是一个三维单纯复形T,T和X的顶点一致且X中的每个体元都是T中单纯形的并集X。对于X的约束四面体剖分T,如果满足每个四面体都符合约束Delaunay,则T就为X的约束Delaunay四面体剖分。

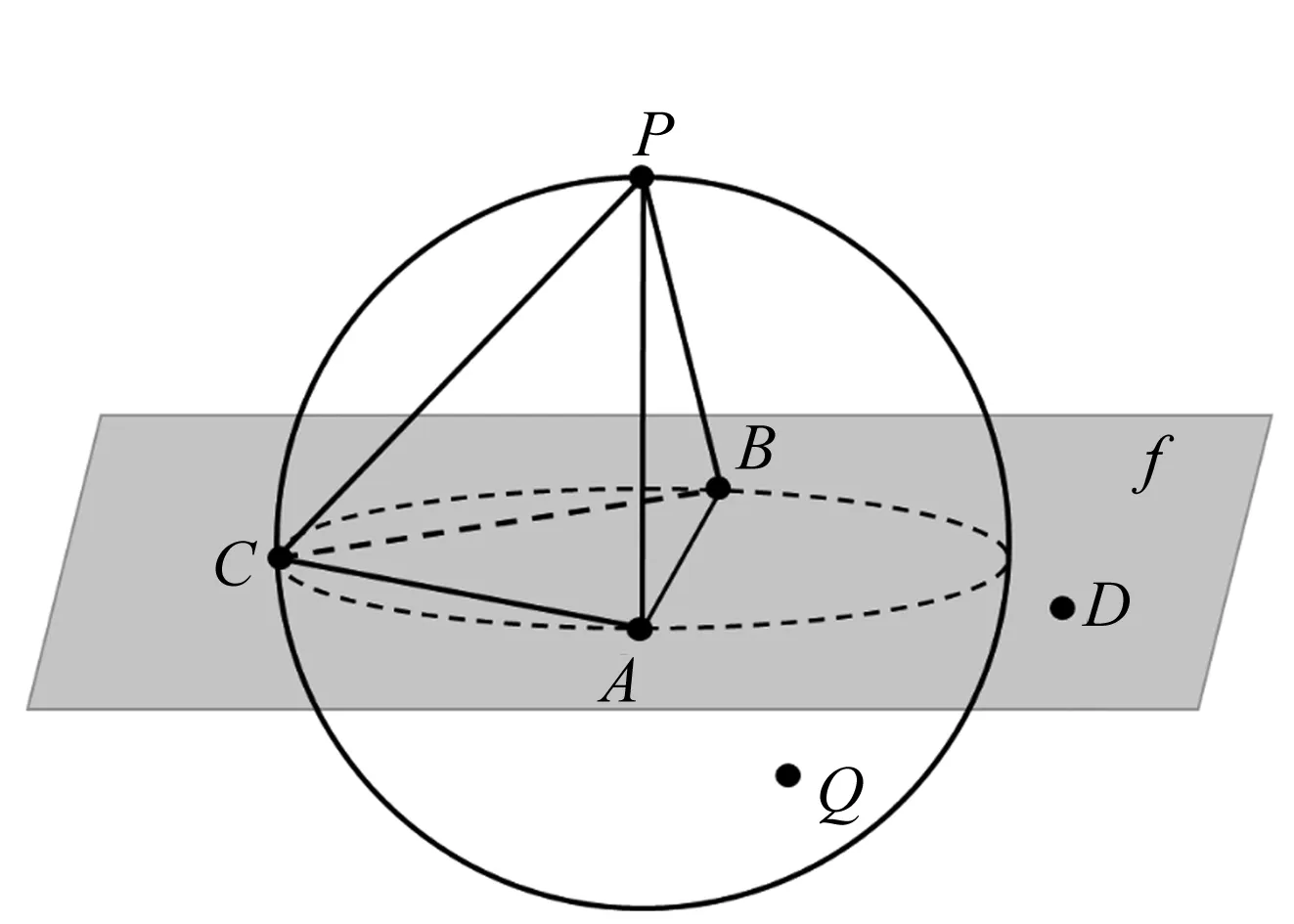
图3 约束Delaunay四面体示意图

Delaunay四面体剖分和约束Delaunay四面体剖分的不同之处在于,对边界多边形内的三角形去掉了局部Delaunay的要求。因此,约束Delaunay四面体剖分保留了很多Delaunay四面体剖分的有利属性[19]。与Delaunay四面体剖分相比,CDT生成所需的Steiner点通常会更少。尤其是当PLC包含一些锐化特征,几个单体会在一个很小的角度(或是二面角)相交时,Delaunay四面体剖分是难以生成的,而且可能需要大量的Steiner点,而CDT可以很容易地处理这种锐化特征。

3.3 特征约束四面体剖分

特征约束是对四面体体元的形状参数化约束控制,实现四面体格网的质量优化。四面体形状参数没有唯一的定义,一般的含义为避免内部存在非常小或非常大的二面角。对于一个单纯形四面体质量判定的最普遍方法是长宽比。图4为单个四面体形状参数图,其中r为四面体外接球半径,h为点到对应三角面的距离。四面体PABC的长宽比是最长边的长度|AC|与最小高度h之间的比值,其中最小高度h是四面体4个顶点到对应平面距离的最小值。TetGen并不是用长宽比,而是选择半径边长比和二面角(两个面的夹角)作为四面体的形状控制,二者相互结合可实现对四面体的特征约束。四面体T的半径-边长比(radius-edge ratio)是外接球半径r与四面体最短边长度d的比值,即为r与|PC|的比值。大多数形状不好的四面体会有一个比较大的半径-边长比值,只有没有短边且体积接近0的扁平四面体薄片[20]会存在较小的半径边长比。薄元四面体形状如图5所示。TetGen采用四面体的最小二面角作为Delaunay细化算法的第二个约束方法,通过Delaunay细化迭代次数来移除薄片。由于具有锐化特征的四面体是永远不会被移除的,因此只有少数畸形四面体会保留下来。

图4 四面体形状参数图

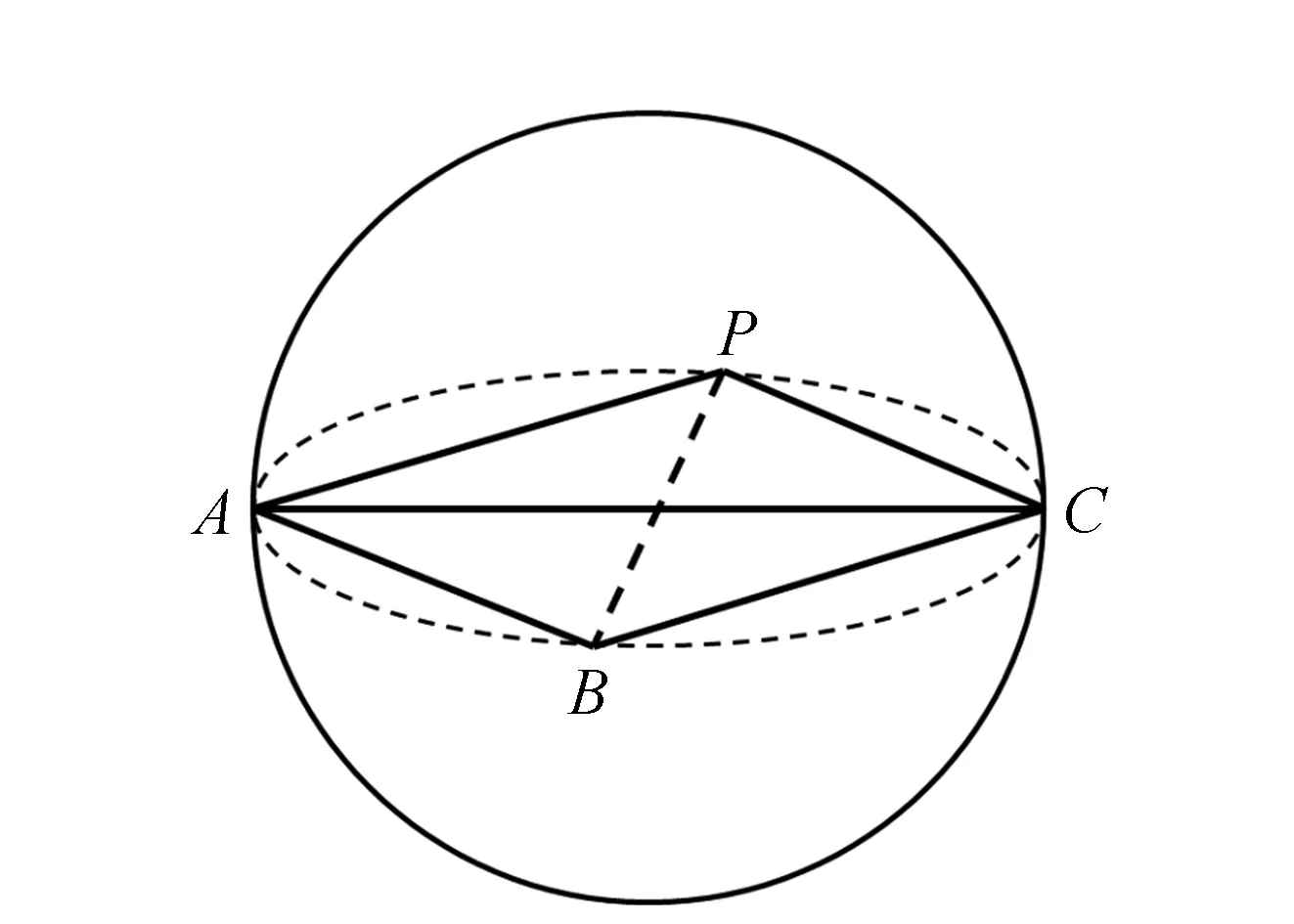
图5 薄元四面体示意图

TetGen采用了一个简单的“爬山”方案来控制四面体形状特征,即只有当生成的新四面体参数值优于当前最差的四面体时才进行局部优化运算。初始化形状较差的四面体列表,若其参数值小于给定的目标值,对其使用局部操作:使用边/面翻转和顶点平滑来删除它们。结合这两种操作,不断迭代实现优化的四面体替换劣质四面体。

4 实验分析

研究区位于陕西省某地区,宽度为706 m,长度为1 811 m。其中钻孔数据数量为39个,地层分界面为5个,地层数量为4层。先对钻孔数据加密,分地层构建多地层表面模型生成约束PLC。利用TetGen进行特征约束Delaunay四面体剖分,向约束边界和地层内部插入节点,恢复约束线和约束面,构建该地区四面体格网地质模型,并对不同约束下的地质模型进行四面体质量分析。

4.1 地层表面约束模型构建

1)钻孔数据预处理。原始钻孔数据一般包含坐标、岩性、深度及方位角等信息。建立地层面Delaunay三角网需要获得钻孔轨迹线上岩性分界点的三维点坐标,故需要对原始数据进行预处理。由于研究区常存在钻孔资料分布不均,采用克里金插值算法对原始钻孔数据进行加密处理。通过插值处理计算新增岩性分界点坐标,构建相对精确完整的地层分界面。

2)地层模型上下边界构建。地质界面的建模本质上是利用面模型实现对地层起伏形态的模拟。目前地层边界面的建模主要采用不规则三角网法[21]。TIN模型结构简单,建模理论成熟,精度高,可视化效果好,适用于地质体表面的几何建模[22]。文中采用Delaunay三角剖分算法构建TIN,TIN由节点、三角形边和三角形面构成。在地质建模中,地层分界点即为节点,对节点进行Delaunay三角剖分,依次建立各地层上下边界面的三维模型。

3)地层模型侧边界构建。地质体侧边生成即利用三角网缝合上下底层曲面,其中基于平行轮廓线的TIN构建方法应用最为广泛。缝合的原理为把两个相邻的平行轮廓线上的点连接生成满足一定要求的不相交三角形,实现单个地层模型的构建。基于平行轮廓线的TIN构建方法有最大体积法、最短对角线法和同步前进法[23]。文中研究的地质体对象为正常产状的岩层,轮廓线大小形状相近,应用最短对角线法构建的三维表面效果较好。

最短对角线法具体步骤为:获取上下轮廓线,判断上下轮廓线顶点数量是否相等,若不相等,在数量少的轮廓线中最长距离的两个顶点之间外推一个顶点,重复以上操作直至数量相等。最短对角线法的空间示意图见图6,在上轮廓线上找到与Pi点距离最近的下轮廓点Qi,判断Pi,Pi+1,Qi,Qi+1组成的四边形对角线PiQi+1和Pi+1Qi长度大小;若|PiQi+1|>|Pi+1Qi|,则构建△PiPi+1Qi和△Pi+1QiQi+1,否则构建△PiPi+1Qi+1和△PiQiQi+1;直到完成所有顶点判断,即实现地层侧边的生成。

图6 最短对角线法示意

4.2 三维地质模型可视化

VTK是一个开源的、支持多平台的软件系统,主要应用于三维计算机图形学和三维可视化。其基于三维函数库OpenGL和面向对象的原理,通过创建.vtk的数据文件格式,为各种数据集类型提供一致的数据表示方案。VTK支持体元绘制,借助于VTK组件库可实现三维地质模型的可视化及几何运算,为实际工程施工及地质灾害超前预报提供可靠参考。

对多地层表面模型进行约束四面体剖分输出.vtk文件,使用VTK组件库实现以四面体为基本体元的地质模型的渲染,地质体模型可视化如图7所示。另外在地学分析中,三维地质切割是三维建模的重要信息交互手段,能够分析矿体的内部结构,揭示地质体内部隐藏的地质信息[24]。三维地质模型的切割主要分为任意平面切割和组合切割。任意平面切割是最广泛的切割方式,组合切割是利用多个平面组合构建出三维地质剖面模型。地质模型组合剖面图如图8所示。借助VTK组件库可快速实现模型切割及剖面可视化。

图7 三维地质模型渲染

图8 组合剖面图

4.3 地质模型四面体质量分析

三维地质模型质量主要与四面体质量相关。在相同地层表面模型条件下,不同特征参数约束所生成的四面体格网质量不同。通过设置3种不同特征参数约束条件,分析四面体格网的质量情况。3种具体参数约束为半径边长比为4.0,同时最小二面角为8°;半径边长比为2.0,同时最小二面角为8°;以及半径边长比为2.0,同时最小二面角为20°的约束,在此分别简称为参约1、参约2和参约3。3种参数约束下的地质模型表面格网如图9所示。

图9 三维地质模型表面格网

地质模型以四面体为基本体元,可根据四面体顶点及地层属性等信息快速实现地层体积计算。通过对实例模型统计计算,可得底层地层的体积为2.01×108m3,第二层地层的体积较小为1.18×107m3,第三层地层的体积为1.99×108m3,最顶层地层的体积为2.61×108m3,总体积为6.73×108m3。对3种参约剖分后的四面体格网的节点数量、四面体数量和模型内存大小统计得到表1。由表1可知,在参约1条件下模型的四面体数量最少,模型节点数量最少,占用储存空间最小。另外通过图9(a)可知,参约1模型表面三角网稀疏,间接反映四面体格网质量较差;参约3条件下,模型四面体数量最多,模型节点数量多,表面格网三角形分布均匀,模型质量较高,但占用储存空间最大。

表1 地质模型数据统计表

为分析不同剖分参数下四面体格网的整体质量,文中以四面体长宽比和线线角两个评价标准定量分析四面体格网质量。四面体长宽比越小代表四面体质量越好。线线角为四面体三角面中两条线的夹角,范围为0°～180°,可间接反映四面体质量情况。由于不同参约下模型四面体总数不同,故将长宽比和线线角划范围按百分比进行统计,结果如图10和图11所示。通过图10可知,参约3条件下在小于4的长宽比范围内,经统计四面体数占量比达85%,明显大于另外两种参数,四面体格网质量更高。在参约3线线角集中在40°～80°,占比达79%,远高于其它两参数的42%和57%。线线角集中在0°或180°附近意味着位于薄元四面体上。由图11可知,参约3下在0°或180°附近的线线角数量很少,薄元四面体数量最少。通过对比3种参约剖分结果,参约3下模型四面体整体质量最高,参约2次之,参约1下模型四面体整体质量最差。本方法利用特征约束可生成不同质量要求的四面体模型,可满足不同地质分析条件的需要。

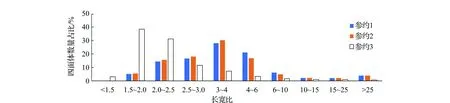
图10 四面体格网长宽比统计

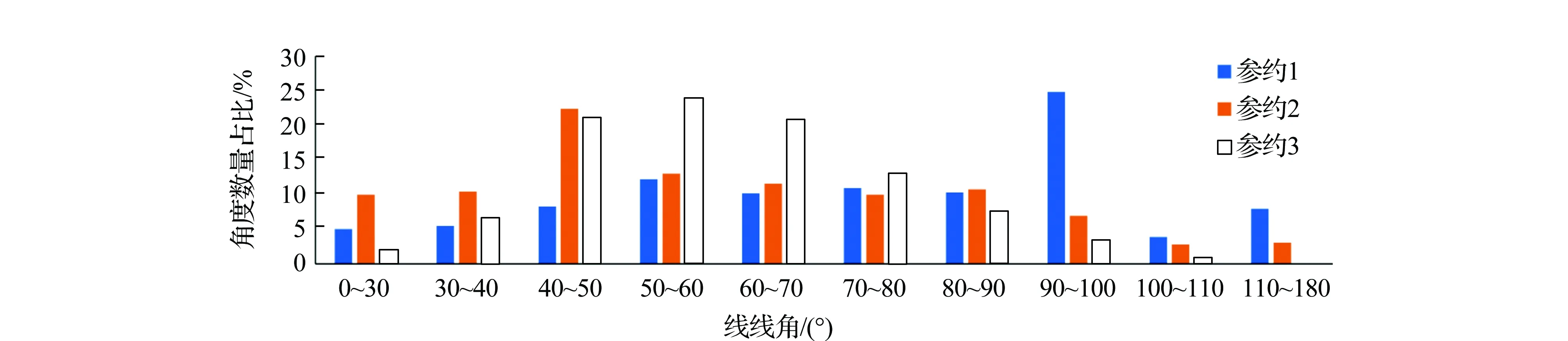
图11 四面体格网线线角统计

5 结 论

基于钻孔数据建立Delaunay三角网生成多地层地质体边界模型,并对其进行约束Delaunay四面体剖分,通过半径边长比和最小二面角大小等特征约束生成网格质量较高的三维地质模型。该模型以四面体为基本体元,可进行数据存储与快速可视化,并能够进行拓扑关系查询、体积计算、剖切面生成、模型切割及有限元分析等空间分析操作。通过实验分析证明了建模方法的有效性和可行性,可为地下矿体开采等工程规划提供数据支持。考虑到地下空间点线面及空洞的复杂性,还需对断层、尖灭等复杂地质体建模进行研究,并将模型应用于地学数值计算分析,为地质灾害模拟及预测提供借鉴。