公路路面LiDAR数据空洞插补的MLSPF方法
2023-11-07刘嘉煌邓兴升
刘嘉煌,邓兴升
(长沙理工大学 交通运输工程学院,长沙 410114)
我国目前的交通设施网正处于建设加速时期,为了提高公路建设和安全运营管理水平,及时精确地获取路面信息并对其做出正确的判断,可通过机载激光雷达(LiDAR)扫描路面,获取道路路面的三维坐标信息,同时也可以检测道路路面的完整性、损毁程度等,为道路的养护和维修提供关键信息[1-3]。激光雷达信号具有一定的穿透性,但是LiDAR获得的道路数据经常由于树木、行人、车辆等地物的遮挡存在着部分数据的缺失,使得路面点云数据呈现出空洞现象从而影响整条道路的完整性,对后续道路标识线提取、智慧道路体系的建设、道路标识点的聚类识别、道路设施改扩建等工作产生不利影响。因此文中对LiDAR数据空洞展开研究,提出道路点云数据空洞填补的移动最小二乘平面拟合方法(moving least square plane fitting method, MLSPF)。
沈晶等[4]提出在数据缺失的周围采用最低点高程值对数据缺失区域进行填充,该方法理论上并不合理。Manry等提出泰森多边形分析法—最邻近插值法[5],该方法由于三维坐标测量的误差,依赖数据缺失周围最近的3个点位置拟合并不能得到最佳平面,甚至存在较大的偏差。张昊等认为,最邻近插值法不适用于点云数据分布太过密集或者点云数据中存在大量空洞的情形[6]。焦嵩鸣等认为距离反比插值法效果不仅会受到距离权重的影响而且对于非规则区域,需要进行分段插值[7]。姚艳丽等研究发现不规则三角网插值法,对于一些包含大量特征的地形,该方法能较精确地还原真实地形,但是在前期需要进行大量数据预处理工作[8]。康帅等提出函数插值法对属性值的估算采用函数中的最小化表面总曲率进行[9],该方法虽然操作简便,计算量较小,但常用于地形情况较平滑的区域和需要二阶导数连续,除此之外插值工作完成之后会对区域的地形地貌有所改变,高程值也会发生变化。张海平等认为空间插值模型的使用,关注的是模型的复杂程度以及模型是否需要满足多个条件假设[10],而该过程较为复杂。MARINONI等提出克里金插值可生成预测表面,还能够对预测结果进行误差评估[11],虽然处理数据空缺区域效果较好,但是数据处理时间较长效率较低。
纵观上述插值方法,采用不同的插值方法对机载LiDAR扫描数据缺失区域处理的完整度和效率各不相同,难以兼顾数据空洞填补的完整性及计算的高效率。因此文中基于文献[5]的平面拟合思路,但不是利用3个点而是利用格网区域中的所有点,基于最小二乘准则求最佳拟合平面方程,最大程度地贴合实际路面情况。利用实际工程中LiDAR公路路面扫描得到的点云数据进行实验研究,结果表明,文中提出的填补路面数据空洞的方法和技术路线具有可行性及技术优势。
1 路面点云数据空洞插补MLSPF方法
路面点云数据空洞填补指的是在各等级公路路面范围内,寻找填补平面,在填补平面内检测是否有数据缺失,若有则对数据空洞部分采用最小二乘平面拟合平面插值,填补路面空洞而生成完整的路面。
1.1 技术流程
基于机载LiDAR点云的路面数字化,首先沿公路延伸方向规划无人机飞行线路进行公路原始点云数据采集,公路原始点云数据量大,其中包括其它非路面的范围和其它地物,如车辆、树木、行人等因素的存在会导致扫描得到路面存在遮挡情况,因而文中采用基于移动最小二乘平面拟合,对离散的点云数据进行格网化插值,从而完成路面数据空洞的填补。主要的技术流程如图1所示。
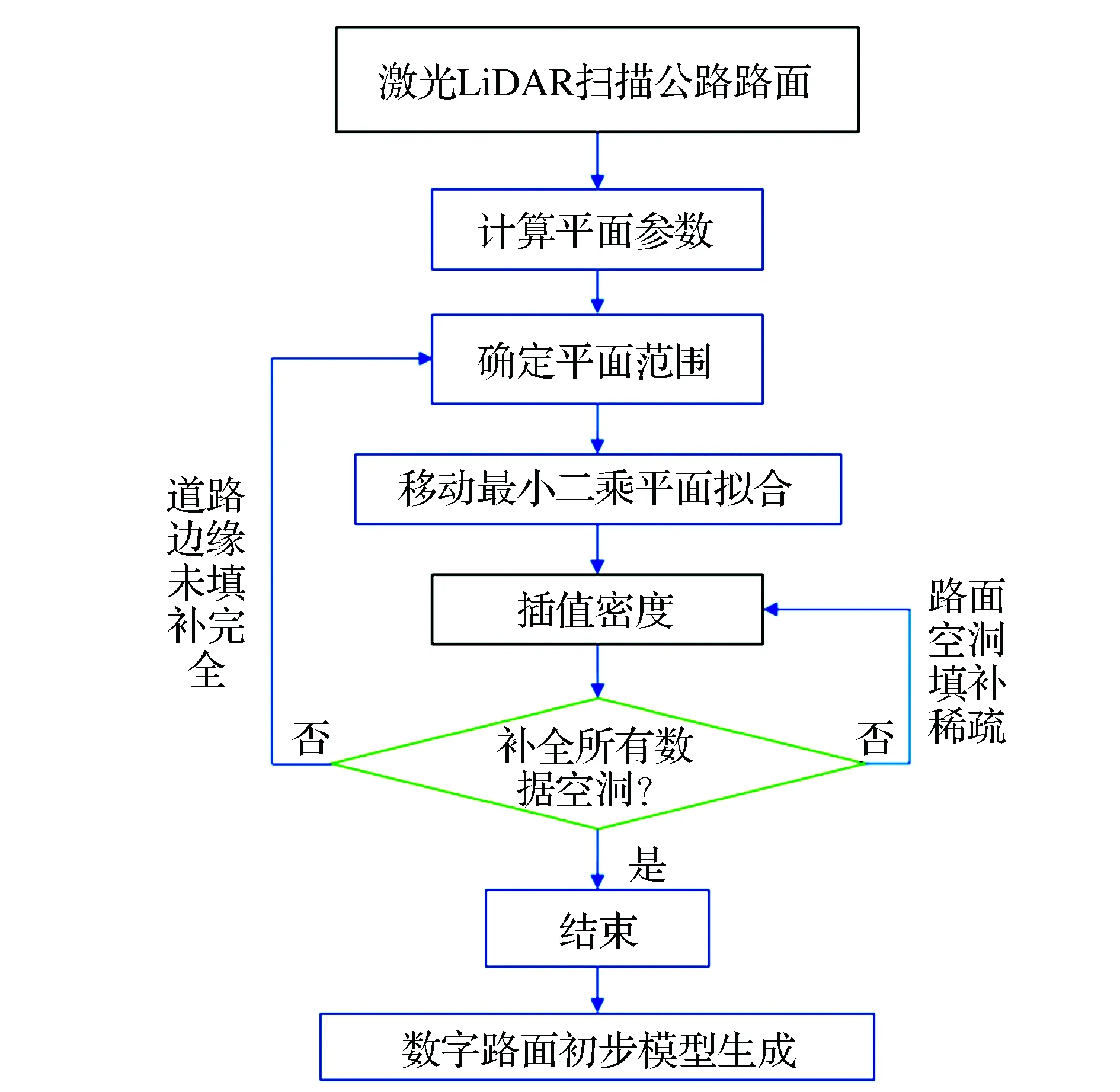
图1 填补道路机载LiDAR数据缺失流程
1.2 最小二乘平面拟合原理
基于公路路面激光扫描得到的数据是离散点云,虽然路面在纵向和横向都有坡度和曲率,但如果将路面分为细小的局部区域,那么这些细小的区域可用平面去近似,设平面方程为:
AX+BY+CZ+D=0.
(1)
若C≠0,则有:
Z=a0X+a1Y+a2.
(2)

设有离散点集{(x,y,z)|(x,y,z)∈(xi,yi,zi),i=1,2,3,…,n-1},按照最小二乘原则,使得式(2)误差平方和最小。
(3)

(4)
化简式(4),写成矩阵形式:
(5)
则a0,a1,a2的解为:
第三,后期维护由所有权人负责。较大规模的工程,一般是建立工程管理机构,由其负责供水管理以及包括管道工程在内的工程维护;小规模的供水工程,一般由受益村自用自管。
(6)
1.3 最小二乘平面格网插值
在机载LiDAR路面扫描过程中,车辆、行人、两旁的树木会遮挡路面而产生路面空洞,需要采用插值算法对空洞区域插值处理。路面出现的点云孔洞,虽然严格意义上来说它应该是一个曲面,但是在面积很小的局部路面区域,可以用平面来近似小块的路面范围。因此,可以利用孔洞周边最少3个点及以上的三维点云坐标,在最小二乘原理下,求得最优拟合平面方程,然后由平面方程插值计算生成孔洞中的点云坐标或栅格结点的坐标。设空间平面方程表示为:
z=Mx+Ny+O.
(7)

X=[MNOT=[BTB-1[BTL.
(8)
求出拟合填补平面后,需要考虑插值平面的范围,范围合适,则空缺处边缘填补越完整;同时插值密度也需合适,此过程可通过控制插值格网大小实现,合适的插值密度才能达到路面数据空洞填补的最佳效果。补全点云孔洞,由离散点云插值计算栅格节点坐标(x,y,z),平面方程作用范围有限,因此采用移动平面拟合插值策略,完成公路路面数据空洞填补,生成路面数字化初步模型。
2 实验与分析
为了验证公路路面激光扫描数据空洞插补方法的可行性,以机载LiDAR获取的长沙理工大学云塘校区凌云路为实验区域,道路坡度为17°、长度为86 m、宽度为12 m;所选取的实验道路走向为东西方向,点云密度为61个/m2,总点云个数为48 270个;首先进行机载航空影像及LiDAR点云数据采集,实验区域的点云数据主要包括了公路、车辆、路旁绿化带等,树木、车辆、行人遮挡情况如图2所示,原始机载LiDAR点云如图3所示。

图2 航空影像

图3 原始机载点云
由于计算效率与计算机硬件配置有关,实验电脑的配置为:Intel(R) Core(TM) i7-4790 CPU ,16GB内存,Windows10 64位操作系统,编程语言为Matlab2022a。
2.1 插值处理
根据最小二乘平面拟合格网插值处理方法,格网大小的设置与插值密度密切相关,若在采集的点云起伏较大的区域,格网必须设置密一点,反之如果采集的点云高程起伏较小,则格网可以设置大一点。文中所选取的实验道路整体起伏不大,并且经过多次的反算调整以及对比得出最优参数是以每个格网范围0.2 m×0.5 m为单位进行平面拟合及插值计算,该网格范围不仅使得计算速度加快而且路面空洞填补效果也是最佳,计算时间仅需0.983 s,处理速度快,效率高,对于路面的数据空洞部分填补较好。移动最小二乘平面插值结果如图4所示。

图4 公路LiDAR点云数据(由MLSPF插值)
图4(b)中色带表示:道路区域的不同颜色代表不同的高程值,下述各个方法的结果与图4(b)相同,且由图4(b)可知,道路数据缺失部分填补完全,道路边缘的齿痕部分填补过后还原效果好,同时路面点云数据分布较为均匀且光滑,能够较完整的呈现道路。
2.2 与其它插值方法对比
Emery等[12]提出插值原理大体过程可描述为:根据数据缺失周围的已知点云数据进行模拟未知点值,代表性方法有:最邻近插值法、克里金插值法、反距离插值法等。以下对4种方法进行计算精度与效率的对比实验。

图5 公路LiDAR点云数据(最近邻插值方法)
克里金插值法具有较强的空间相关性,王标极等[15]提出需通过对已知样本进行加权平均来估计平面上的未知点,使得估计值与真实值的数学期望相同且方差最小。
(9)
式中:Z(x0)为未知点的估计值;Z(xi)为采样点xi属性;λi为各采样点权重系数,满足无偏性且在无偏条件下方差最小的要求。克里金算法需要的计算时间非常长,需要4 832.766 s,由此可知克里金算法复杂,数据处理量巨大。由图6可知该算法处理过后的路面点云分布合理且路面较为平滑,路面数据空洞处填补效果较好。因此该算法能够有效解决基于机载LiDAR获取的公路路面数据存在遮挡的情况,但是缺点也很明显,即计算过程复杂,效率较低。
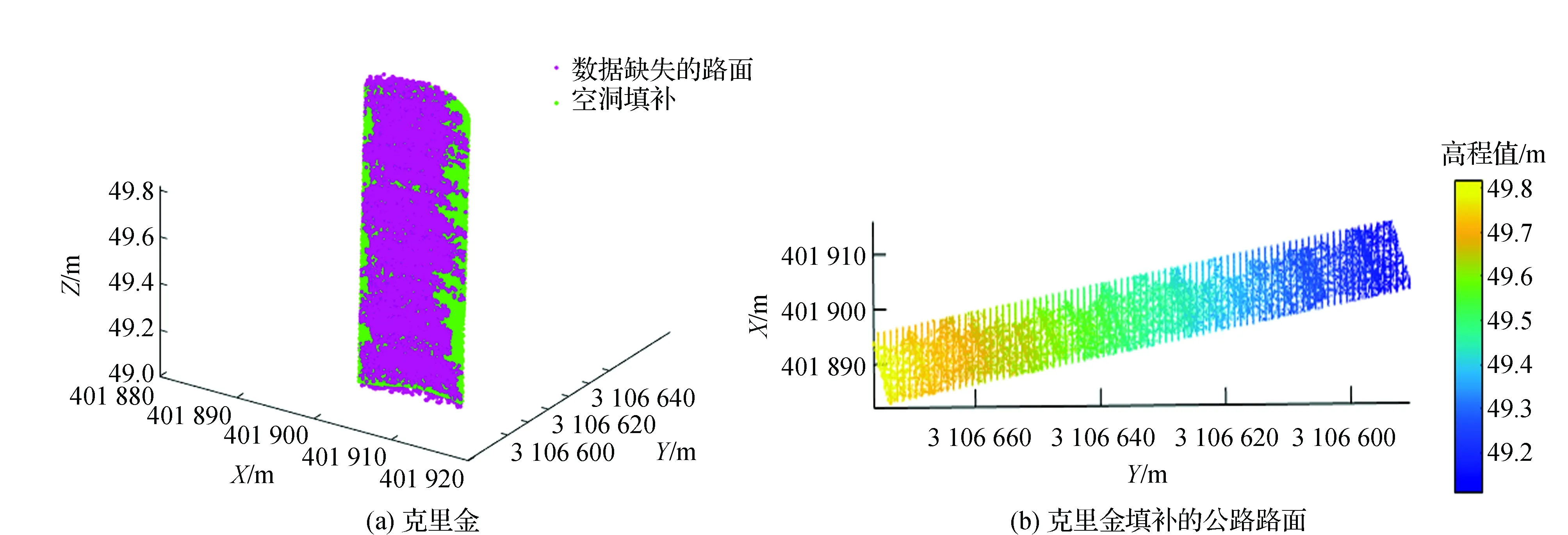
图6 公路LiDAR点云数据(克里金插值)
反距离加权插值法( inverse distance weighting,IDW)作为最常用的插值方法,是由美国国家气象局提出以待插值点与实际观测样本点之间的距离为权重的插值方法,计算式为:
(10)


图7 公路LiDAR点云数据(反距离加权插值)
4种方法的公路路面填补点云数量和计算时间如表1所示。

表1 本研究方法与其他方法填补效果对比
2.3 空洞填补精度对比
由于路面激光扫描存在数据空洞部分,因此数据缺失部分的数据真实值无法获得。为了评估本研究方法的插值精度以及有效性,选取一段数据完整的道路作为真实值,在路面上人为挖空若干处路面数据形成空洞,分四周边有点云数据和无点云数据两种情况,用以模拟机载LiDAR获取路面点云存在遮挡情况。参照完整的实测路面数据作为对比真值,从而可验证各个填补方法的效果,并且通过两者拟合得到的R2(拟合优度)、均方根误差(RMSE)、误差平方和(SSE)等精度评价指标,并将其作为插值结果的评价指标对4种方法的插值结果进行评定,插值精度由R2、RMSE、SSE指标来度量,误差值越小说明方法的插值精度越高,拟合优度R2越大表示填补的路面数据愈接近真实值。
如图8为截取的完整公路路面LiDAR点云数据,图9为人为挖空若干处的路面数据,包含了道路数据空洞边缘无点云数据(A侧)和道路数据空洞边缘有点云数据情况(B侧)。

图8 完整公路路面LiDAR点云数据
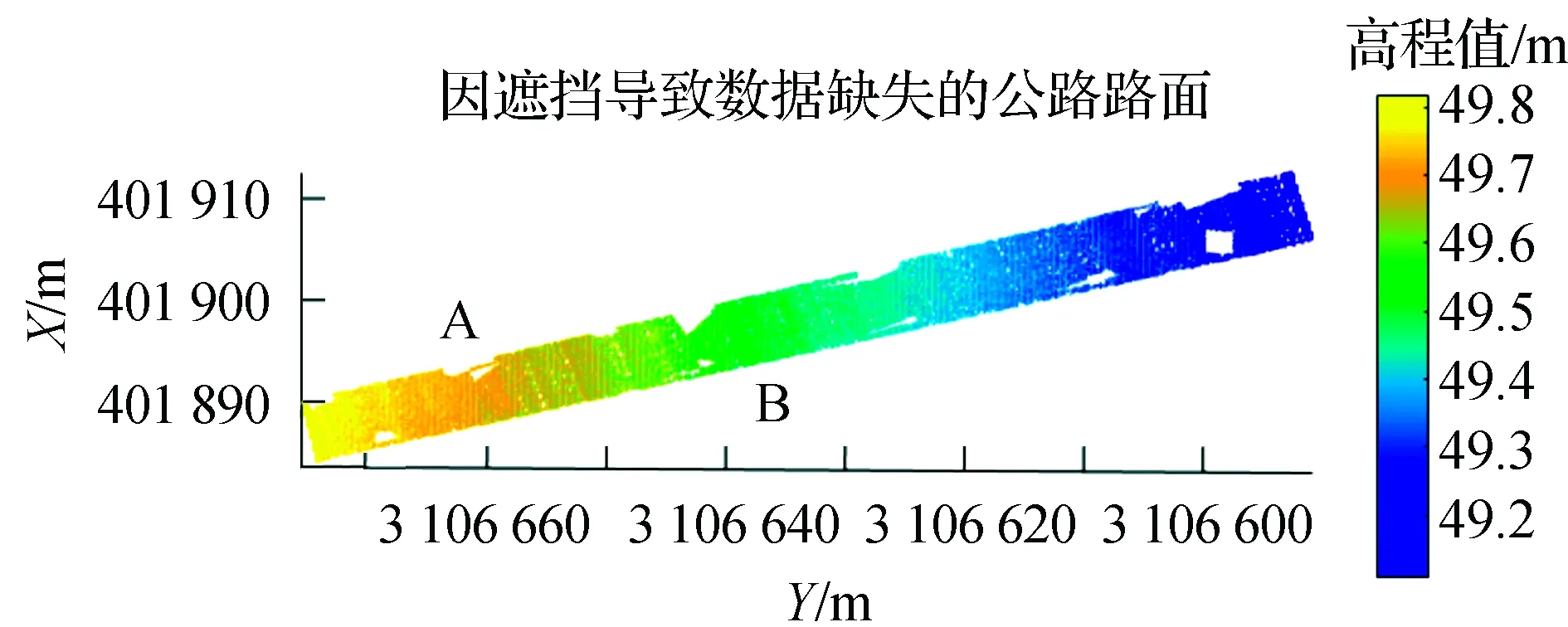
图9 公路路面点云数据缺失
最近邻点方法填补路面空洞速度较快,计算时间仅仅需5.534 s,但是由图10可看出最邻近点填补路面空洞效果较差,虽能够填补四周边有点云数据的空洞部分,但是对于道路边缘一侧无点云数据存在的空洞部分填补效果差,并且对于路面边缘数据缺失的填补伴有齿痕出现,并不平滑。通过填补路面与真实路面对比得到最邻近点填补路面空洞方法的各项误差指标如下:R2=0.984 9、SSE=10.75、RMSE=0.022 38 m。
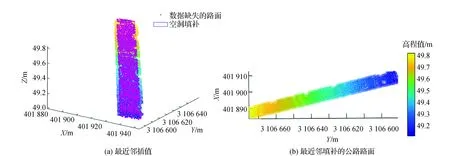
图10 最邻近点填补
克里金方法填补路面空洞速度很慢,计算时间非常长,需918.433 s,但是由图11可看出克里金方法填补路面空洞效果非常好,路面中分为两种情况的数据空洞都已填补完成,并且路面边缘填补过后无齿痕出现,路面平滑性好,但是缺点也非常明显,即计算过程复杂,耗费时间长。通过填补路面与真实路面进行对比可得到克里金填补路面空洞方法的各项误差指标如下:R2=0.988 3、SSE=7.87、RMSE=0.019 63 m。
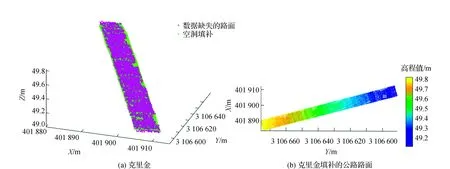
图11 克里金填补
反距离加权方法填补路面空洞速度较慢,计算时间较长,需12.277 s,但是由图12可看出反距离加权插值法填补路面空洞效果与最近邻点填补方法效果类似,填补效果较差,不能完全将四周边有点云数据的空洞完全填补,并且路面边缘一侧无点云数据的路面空洞填补效果不明显,同时路面边缘伴随齿痕出现。 通过填补路面与真实路面进行对比可得到反距离加权填补路面空洞方法的各项误差指标如下:R2=0.986 1、SSE=15.85、RMSE=0.022 24 m。

图12 反距离加权填补
MLSPF方法填补路面空洞速度极快,计算时间较短,仅需0.805 s,由图13可看出格网插值效果非常好,用时短。四周边有点云数据的空洞完全填补,并且路面边缘一侧无点云数据的路面空洞同样完全填补,同时无齿痕出现,平滑效果好。通过填补路面与真实路面进行对比,可得到移动最小二乘法平面拟合格网插值填补路面空洞方法的各项误差指标如下:R2=0.986 4,SSE=8.97,RMSE=0.021 17 m。

图13 MLSPF方法插值填补
由表2的R2、RMSE、SSE、计算时间等综合指标可知,克里金方法计算精度虽高但计算时间太长,相比最邻近点插值和反距离加权插值,MLSPF方法在计算精度与计算时间两方面都具有显著优势。由此可见文中提出的路面数据空洞填补MLSPF方法速度快,填补效果好,并且精度较高。

表2 4种方法空洞插补精度对比
4种方法的插值精度对比如表2所示。
图14、图15为采用不同方法对实验区域、验证区域进行公路路面数据空洞处填补的结果整合图,图的左侧为实验区域,右侧为验证区域。由图14、图15可看出,MLSPF方法填补效果几乎等同于克里金插值算法。
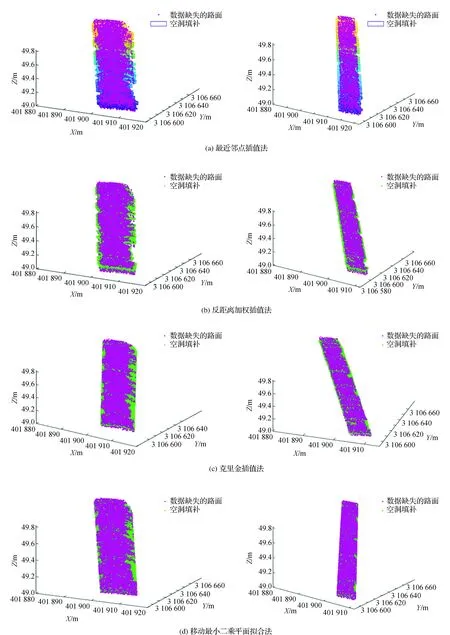
图14 不同方法的插值填补结果整合
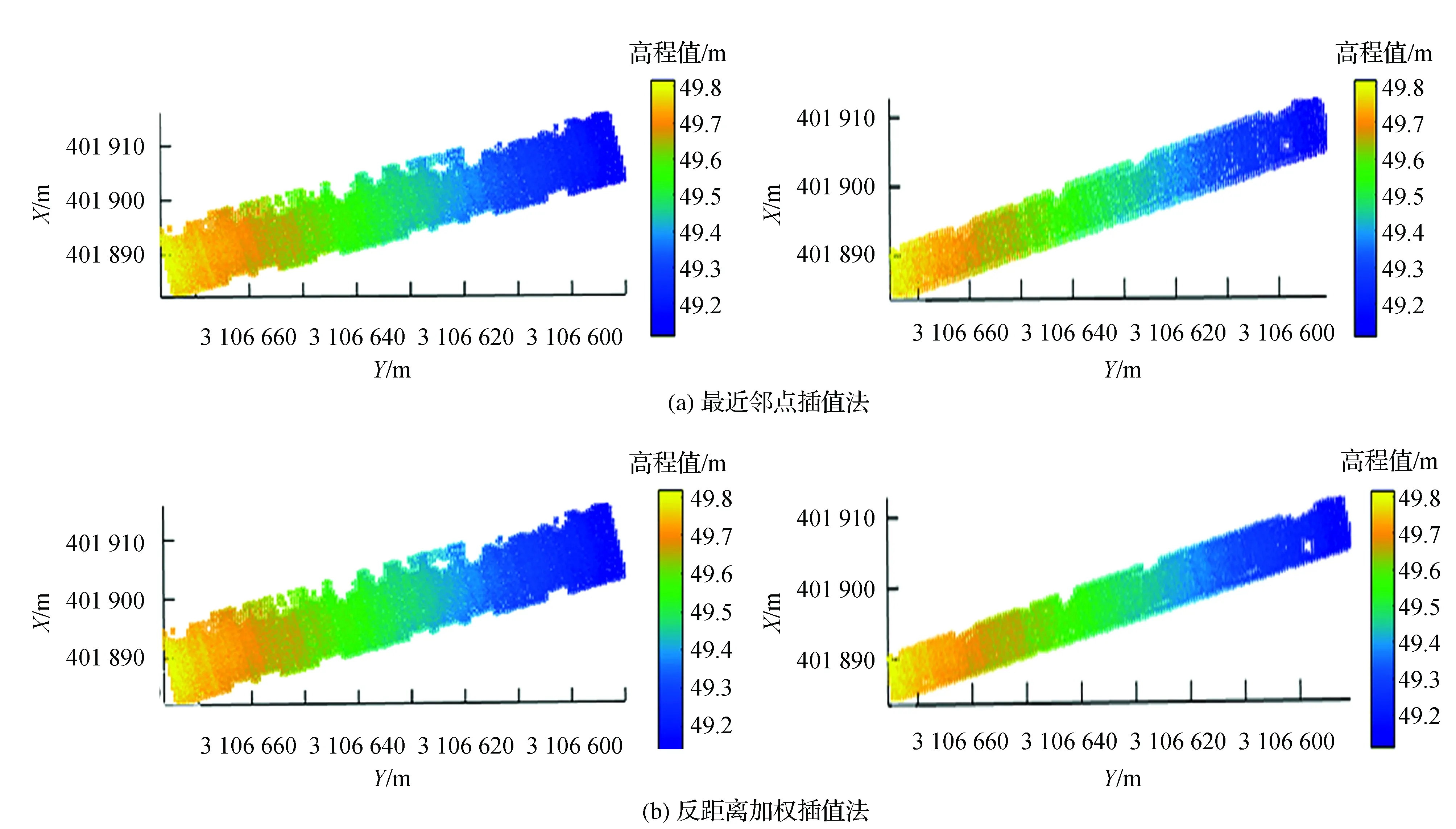
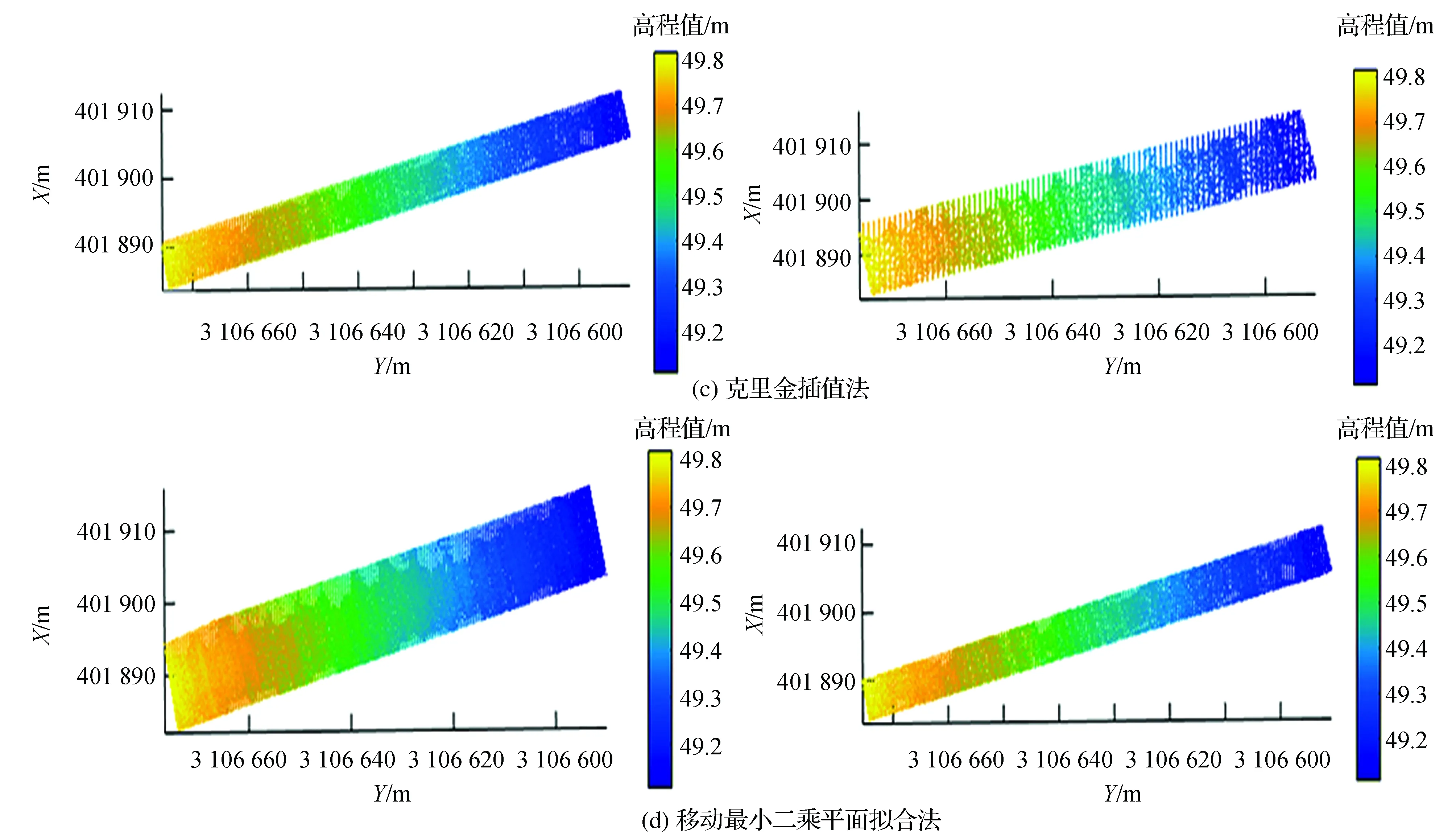
图15 不同方法的插值填补二维结果整合
3 结 论
公路路面LiDAR扫描获取的点云数据,在采集过程中因为地物遮挡等因素,导致路面存在局部数据空洞以及路面边缘数据缺失的情况。针对该问题,文中提出MLSPF方法,采用移动最小二乘平面拟合格网对数据缺失处插值处理,并对结果进行对比分析,得出以下结论:
1)基于公路路面激光扫描数据,利用公路路面划分格网范围内全部的点云,在最小二乘原理准则下求得最大程度贴合路面情况的数据缺失填补面,然后采用网格化拟合插值,从而解决因为地物遮挡导致的路面数据空洞问题,最终恢复原始的完整公路路面。
2)实验表明,基于公路路面激光扫描数据空洞插补MLSPF方法解决路面数据空洞的方法具有可行性和可靠性,数据填补效果好,精度高,效率快,公路路面还原度好,与实际路面起伏形状一致,可为路面数字化提供新的思路与方法。
3)通过与极具代表性且常用的插值模型进行对比,可知MLSPF方法在精度和效率两方法都具有显著优势,不仅可作为道路数据空洞填补应用中可选择的方法之一,并且一定程度上能够为其他类型的数据缺失场景提供方法参考。
4)本方法的局限在于对格网方向的选定、是否需要沿着道路行进方向设置格网,并且针对不同区域是否能采用不同参数的各个单位进行拟合等问题未进行更深层次的研究,在后续工作中以上问题将是进一步研究的重点。
