点群目标空间分布主方向定量描述模型

李 静,禄小敏,刘文蕊,李驿言

( 1. 兰州交通大学 测绘与地理信息学院,兰州 730070;2. 地理国情监测技术应用国家地方联合工程研究中心,兰州 730070;3. 甘肃省地理国情监测工程实验室,兰州 730070 )

点群是地图中至关重要的一类空间地物,成群分布的岛屿、湖泊、沙丘、散列的居民地及各种设施点等在小比例尺地图中均以点群的形式呈现[1]。点群的分布具有一定的方向特征,点群分布方向的判断和识别在地图制图综合、空间推理、空间查询、空间分析与规划等领域具有重要意义[2]。

根据研究对象的不同,可以将已有的方向关系研究分为面向单目标的空间方向关系研究和面向群组目标的空间方向关系研究,前者成果较多且比较成熟,后者成果相对较少且多集中于群组目标空间方向关系的定性描述。在已有的点群目标空间方向关系研究中,文献[3]基于凸壳理论计算点群目标间的空间关系;文献[4]利用点群目标凸壳的最小外接矩形长轴方向表达点群分布的主方向;文献[5]在生成点群目标标准差椭圆的基础上以长轴方向作为点群的主要分布方向;文献[6]利用点群目标凸壳的直径方向来表达点群分布的主方向;文献[7]以主骨架线的分布方向表示点群目标的分布方向。综上所述,已有算法大都是在近似拟合点群外部形态的基础上,以较长轴方向代替点群的主方向。忽略分布密度对点群目标空间方向关系的影响,计算所得方向会出现与实际分布方向不符的情形(见图1)。

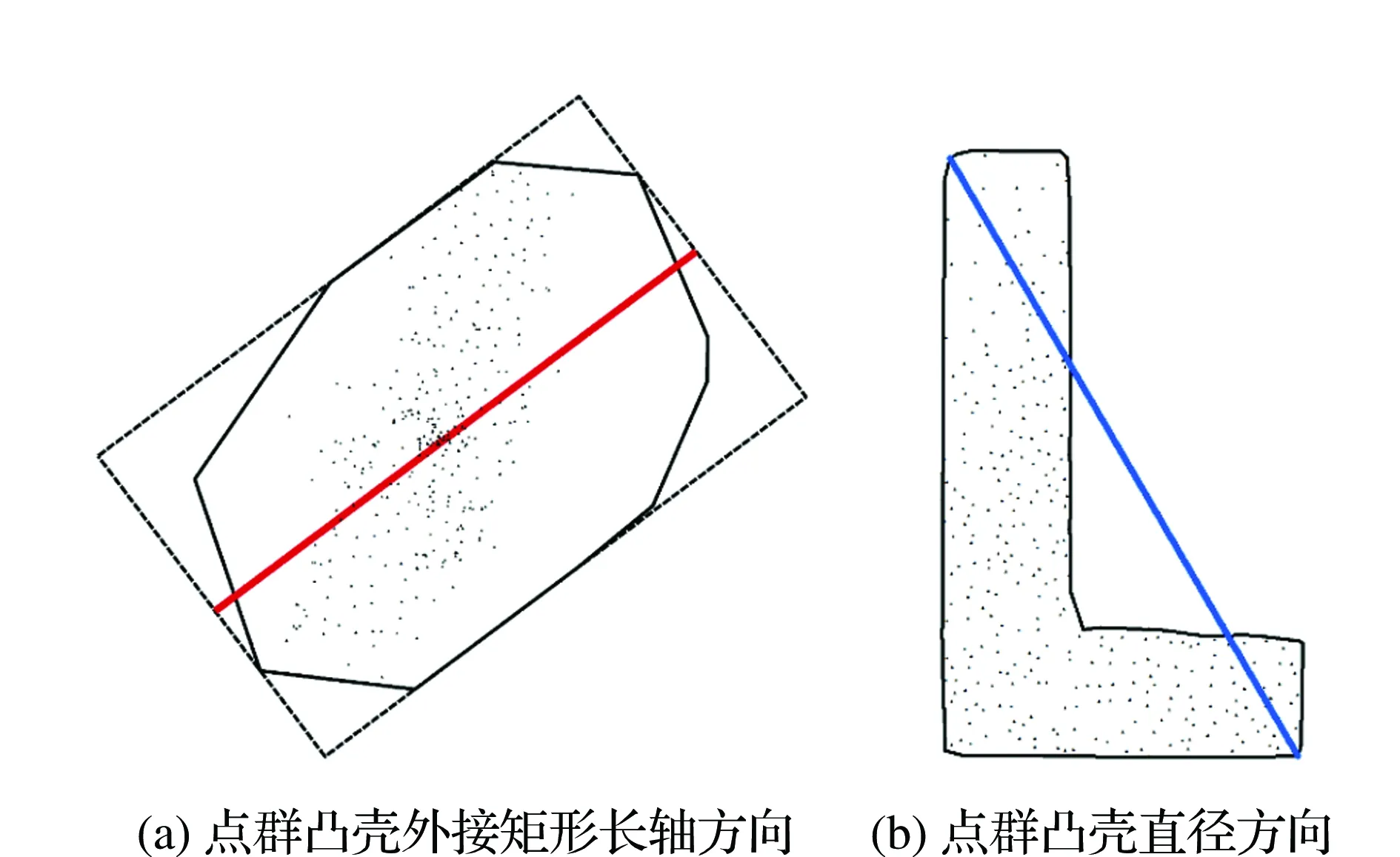
图1 计算所得点群目标主方向与实际不符的场景

依据点群分布密度构建方向玫瑰图,不仅能直观地反映点群在各方向上的密度分布情况及主方向,亦可以对主方向进行更为准确的定量描述。为此,文中以点群为研究对象,基于其密度特征构建方向玫瑰图,在定性描述空间分布主方向的基础上,利用统计加权算法并引入统计学中的置信区间,提出一种更加符合人类认知的主方向定量描述方法。

1 算法流程

算法主要由3部分构成:①依据密度分布状况,构建点群的方向玫瑰图;②以方向玫瑰图为基础,利用统计加权算法计算点群主方向;③引入置信区间,计算点群主方向分布范围。其主要流程如图2所示。

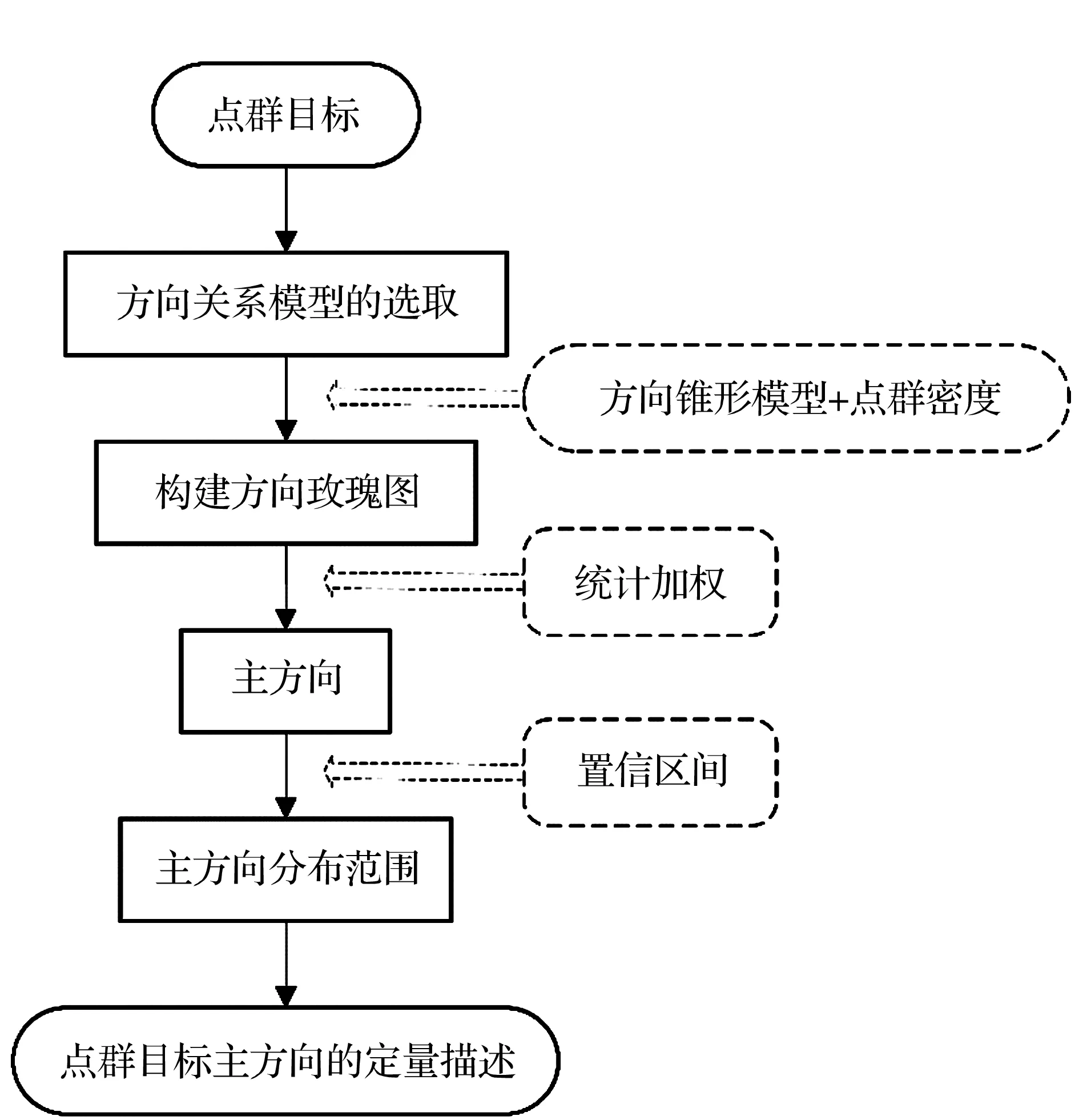
图2 点群目标分布主方向定量描述模型流程

2 点群目标分布主方向定量描述模型

2.1 方向关系模型的选取

空间方向关系模型是描述和计算空间方向关系的有力工具。目前空间方向关系模型主要有基于投影的模型、方向Voronoi图模型和锥形模型。

基于投影的模型是将空间目标投影到特定的坐标轴上,利用投影后目标间的方向关系去近似表达原始目标间的方向关系,将空间目标投影到水平坐标轴和垂直坐标轴上,可将空间划分为N、NE、E、SE、S、SW、W、NW、Same 9个矩形方向区域。该模型较好地顾及了空间参考目标的形状和大小,但方向划分结果与人类认知不符且未考虑目标间距离对空间方向关系产生的影响[8]。方向Voronoi图模型通过计算目标间指向线法线的 Voronoi图来描述目标间精确的方向关系[9-11]。该模型描述空间方向关系精确,但基于方向Voronoi图的模型可视域受限,当可视域外的部分图形发生变化时角度不能随之改变,且模型复杂,计算过程繁琐。锥形方向关系模型通过将空间参考点及其周围的区域划分成若干方向片,依据源目标与若干方向片的“交”来确定方向关系[12]。该模型简单,对方向和距离的综合判断较准确,由于该模型是将参考目标抽象为一个点,故更适合于表达点目标间的方向关系。

锥形方向关系模型中,常用4方向、8方向、16方向来描述空间目标间的方向关系。通过实验对比发现,16方向锥形模型更能反映点群的密度分布和主方向,因此,文中选用16方向锥形模型来描述点群目标的空间分布主方向。

2.2 方向玫瑰图构建

风向玫瑰图,因其外形酷似玫瑰而得名,也称风向频率玫瑰图,它是依据某地某一时间段内风向的统计状况按一定比例绘制而成的风向分布图,多用16方位表示[13]。风向玫瑰图中,线段最长者(外面到中心的距离最大)即为当地主导风向。如图3所示,南方到中心的距离最大,故当地主导风向为南风。

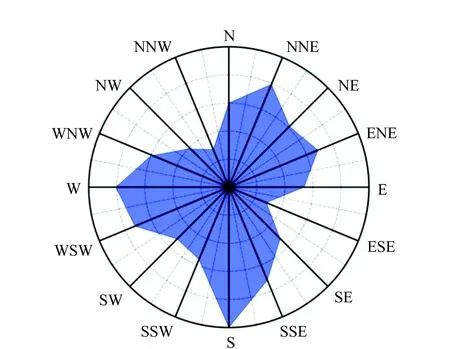
图3 风向玫瑰图

利用风向玫瑰图原理,在计算得到点群各方向分布密度的基础上生成方向玫瑰图,方向玫瑰图可直观地反映点群分布的主方向。点群方向玫瑰图的构建过程如下所述:

1)生成点群目标的凸壳。生成点群目标的约束Delaunay三角网,利用动态阈值“剥皮”法,将Delaunay三角网中外围边长大于某一阈值的非特征边依次删除,最终得到的点群分布边界即为点群目标的凸壳。

2)构建方向关系模型。找到点群目标凸壳的质心,以凸壳质心为参考目标,将连续360°的方向描述离散到对应的16方位,构建16方向锥形模型。

3)计算方向密度,对密度进行归一化处理。如图4所示,点群散落在16方向锥形模型的各个方向片上,统计落在各方向片上点的个数,计算各方向片上点群的密度(各方向片上点的个数与点群总个数的比值)。以落在某方向片内的密度最大值为基准,对各方向上的密度值进行归一化,将归一化后的各密度值描在坐标轴上,使方向玫瑰图各端点即归一化后的各方向密度值均落在以质心为原点、半径为1的圆内。如图4所示,16方向锥形模型下,点群密度最大方向在南方,故以南方密度值为基准,对各个方向上的密度值进行归一化处理。

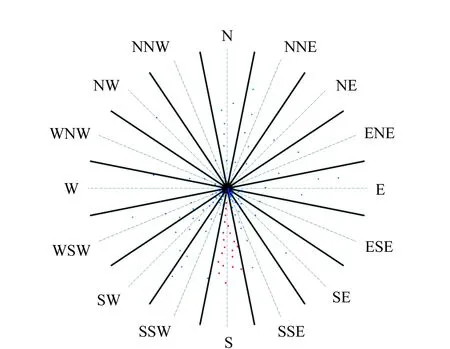
图4 点群分布密度图

4)生成方向玫瑰图。顺次连接相邻方位的各端点,连接生成的宛如玫瑰的闭合折线即为方向玫瑰图。图5即为图4点群在顾及密度分布的基础上生成的方向玫瑰图。

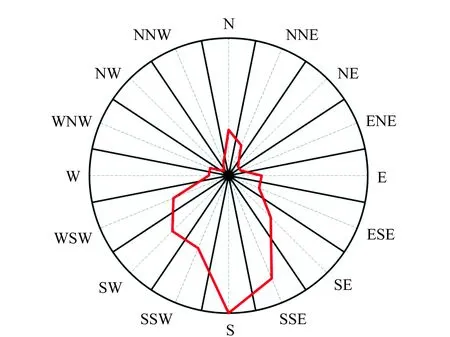
图5 方向玫瑰图

如图5所示,在方向玫瑰图中,南方到中心的距离最大,故图4的点群主要分布在南方。

2.3 点群目标分布主方向定量计算

空间关系的定量描述是利用方位角、象限角等较精确地表达空间目标的方向关系。方位角是指从坐标北方向起,依顺时针方向旋转到目标方向线之间的夹角。本文借用方位角概念并规定:从直角坐标系X轴正半轴起,依逆时针方向旋转到目标方向线之间的角度称为方位角,取值范围为0°～360°[14]。

2.3.1 点群主方向

点群的方向玫瑰图由多边形构成,求点群分布的主方向即为求多边形的主方向。目前,求多边形主方向的方法主要有最长边法、加权平分线法、最小MBR方法、基于墙的均值法以及统计加权法[15]。最长边法以多边形的最长边方向作为多边形的主方向。加权平分线法通过计算多边形中最长直径与次长直径两条边方向的加权平均值来表达多边形的主方向。最小MBR方法以多边形最小MBR中的较长边方向作为多边形的主方向。基于墙的均值法通过计算每条边方向角度与权重(即它的长度)乘积之和的平均值来表达多边形的主方向。统计加权法在测试一系列预选方向的基础上计算每个预选方向的权重(多边形每条边在最大角度偏差系数内对预选方向的贡献之和),计算得到权重最大的预选方向即为多边形的主方向[15-16]。

对点群而言,某方向上一定角度范围内的点会影响主方向的分布。统计加权法考虑多边形每条边在最大角度偏差系数内对预选方向的影响及每条边的长度和角度,以此为基础计算多边形的主方向,不仅能较好地避免长边误差的干扰,具有较高稳定性,而且能顾及某方向周围一定角度范围内的点对主方向的影响,故本文利用统计加权法求方向玫瑰图多边形的主方向。

如图6所示,OB为预选方向,最大角度偏差系数为β,将多边形的每条边平移至以O为起点。若该边在OA边与OC边之内,则对此预选方向有贡献,参与贡献值的计算;若该边方向等于预选方向,那么该边的长度即为贡献值;若该边的方向在最大偏离处,则对预选方向贡献为0;在同方向与最大偏离方向之间,贡献程度线性衰减。

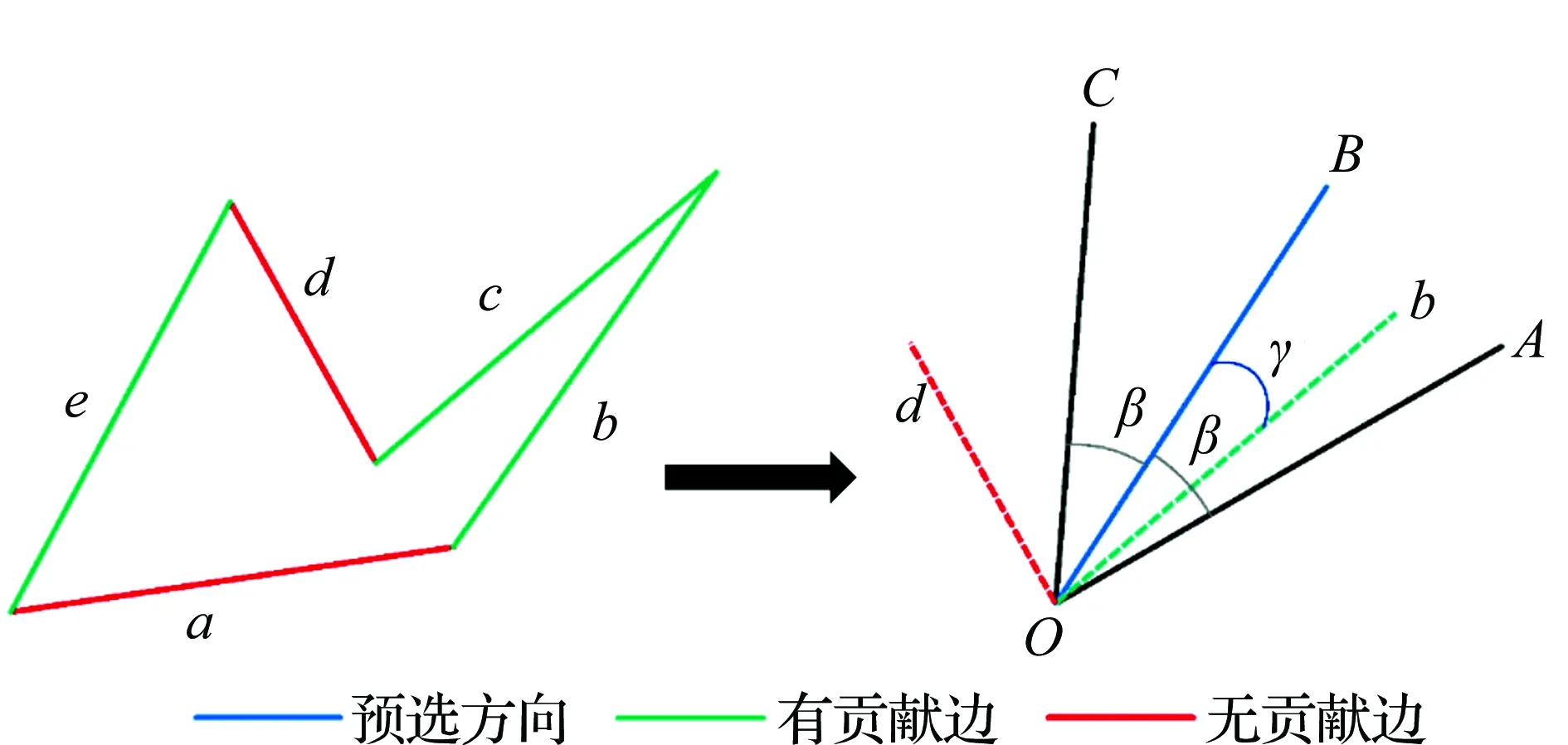
图6 统计加权法

(1)

式中:Ci为贡献值;β为最大角度偏差系数;γ为该边与预选方向之间的夹角;li为边长。

基于统计加权法求点群分布主方向的算法步骤:

1)规定步长,测试预选方向。步长为测试预选方向过程中的固定间隔角度,取值与结果精度相关。根据计算结果的精度需要,本文以1°为固定步长,对0°～360°之间的一系列预选方向进行测试。

2)确定角度偏差系数。角度偏差系数的取值β对主方向结果有一定影响,对其不断进行调整,使得多边形主方向计算结果尽可能准确,最终确定经验值β= 30°。

3)计算各边对预选方向的贡献值。依据式(1)分别计算多边形各边在一定角度偏差内对每个预选方向的贡献值。

4)确定多边形的主方向。统计加和多边形各边对每个预选方向的贡献值,得到各预选方向的权重,对权重进行升序排列,权重最大的预选方向即为主方向。

利用统计加权法计算得到图5多边形权重最大的预选方向为271°,则图4点群大致分布在约271°的方向上。

2.3.2 点群主方向分布范围

为避免个别点分布对主方向计算结果带来的偏差,采用方向分布范围来代替单一角度值。显著性水平α是估计总体参数落在某一区间内可能犯错误的概率,是在进行假设检验时事先确定的判断标准,最佳取值为0.05。置信区间是由样本统计量所构造的总体参数的估计区间,该区间可反映一定概率下此参数的真实值落在测量结果周围的程度。引入显著性水平与置信区间的概念,在得到主方向单一角度值的基础上计算分布区间,能为点群分布主方向提供可接受的范围。在显著性水平α= 0.05下,计算得到图4点群主方向的分布范围为(256.42°～285.58°)。

3 实验与讨论

为验证模型的适用性,选取两组不同分布形态的点群进行实验。分别对两组点群构建16方向锥形模型,得到点群的分布密度图及相应的方向玫瑰图。 由图7可知,点群1主要分布在南方,点群2主要分布在西南方。

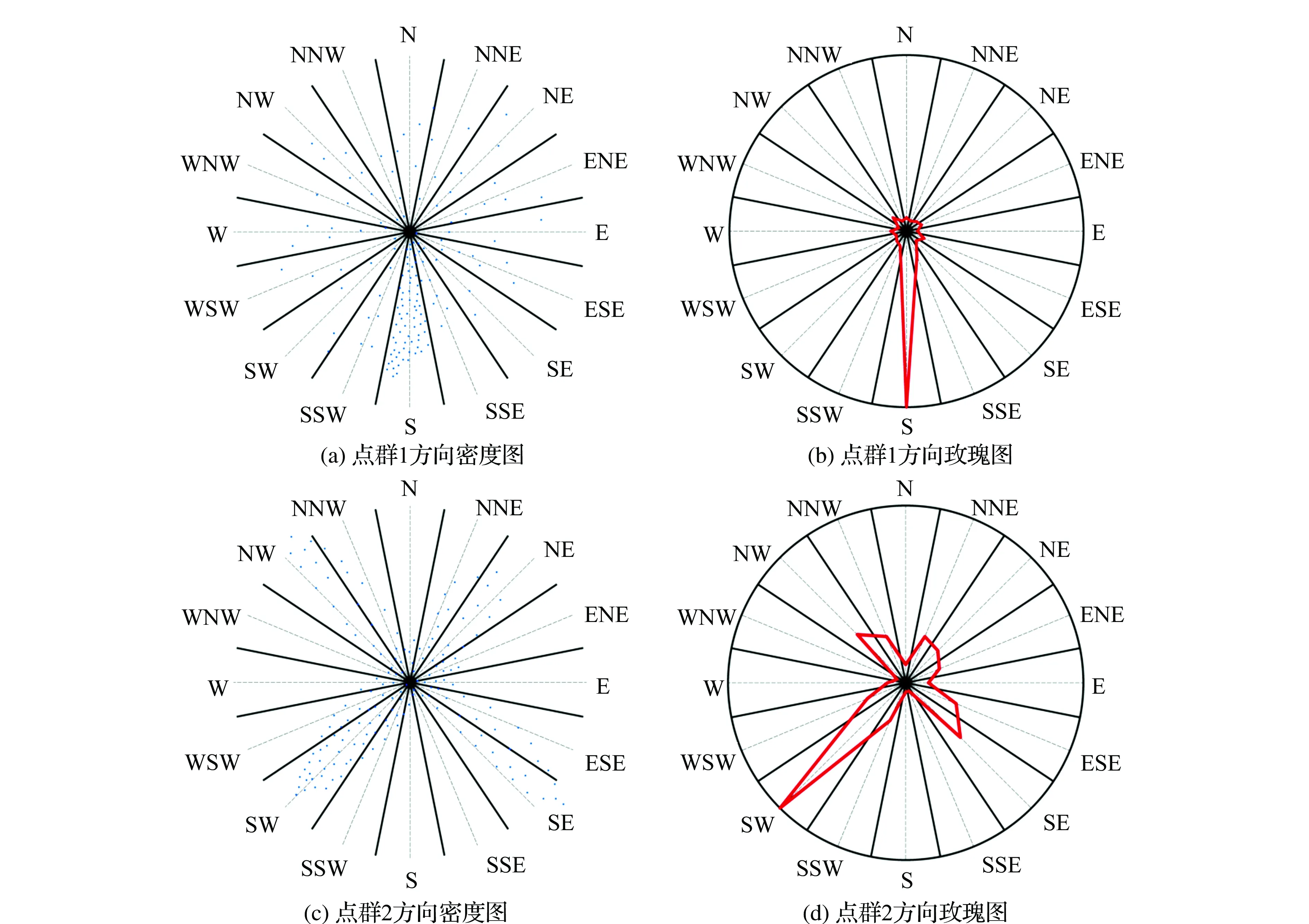
图7 点群方向密度图及对应方向玫瑰图

利用统计加权法分别计算点群1与点群2方向玫瑰图各边对各预选方向的贡献值(见图8),统计可得点群1与点群2方向玫瑰图各边对预选方向贡献值最大的候选方向分别为272.00°、232.00°,故点群1与点群2的主方向分别为272.00°、232.00°。在显著性水平α= 0. 05下,计算得到点群1与点群2分布的主方向范围分别为(257.46°～286.54°)(219.24°～244.76°)。

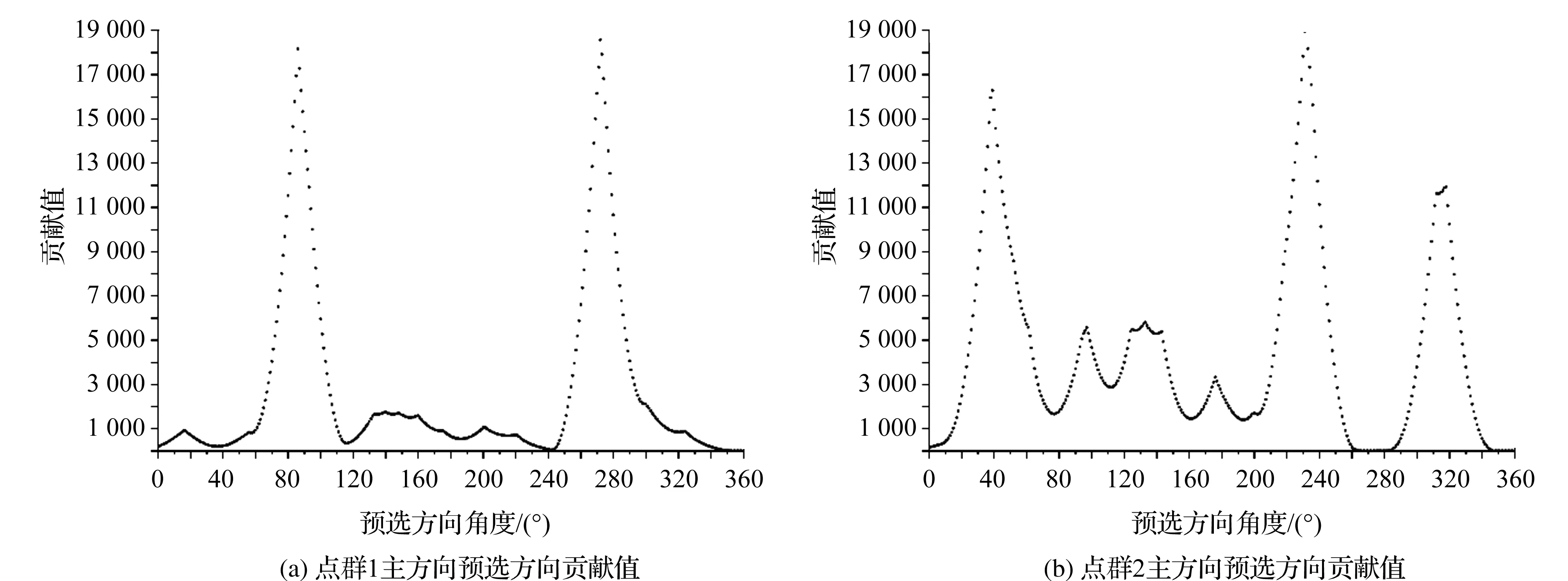
图8 点群主方向预选方向贡献值

为了进一步验证本方法的合理性,将本方法与基于凸壳的最小外接矩形长轴与水平轴的夹角方法、基于凸壳的直径与水平线的夹角方法以及基于标准差椭圆的长轴与X轴的夹角方法的方向计算结果进行了对比,结果见表1。

表1 点群主方向计算方法及结果

由表1可知,基于凸壳的最小外接矩形长轴与水平轴的夹角方法计算得到的点群1与点群2的主方向分别为23.05°、177.95°;基于标准差椭圆的长轴与X轴的夹角方法计算得到的点群1与点群2的主方向分别为62.71°、146.70°;基于凸壳的直径与水平线的夹角方法计算得到的点群1与点群2的主方向分别为53.10°、135.48°;本方法计算得到的点群1与点群2的主方向分别为272°、232°,主方向分布范围分别为(257.46°～286.54°)(219.24°～244.76°)。

空间分布主方向的判断与确定依赖于人类认知,通过心理认知实验验证模型的适用性。实验以问卷形式进行,要求被调查者从表1的计算结果中分别选出点群1和点群2的主方向。因地图学专业人员与其他人员对地图认知存在差异且对方向的敏感度不同,故实验将人群分为地图学相关专业与非地图学相关专业两类。实验样本数为 566个,有效样本数为 563个,其中,47%为地图学相关专业人员,53%为非地图学相关专业人员,人群认知统计结果见表2。

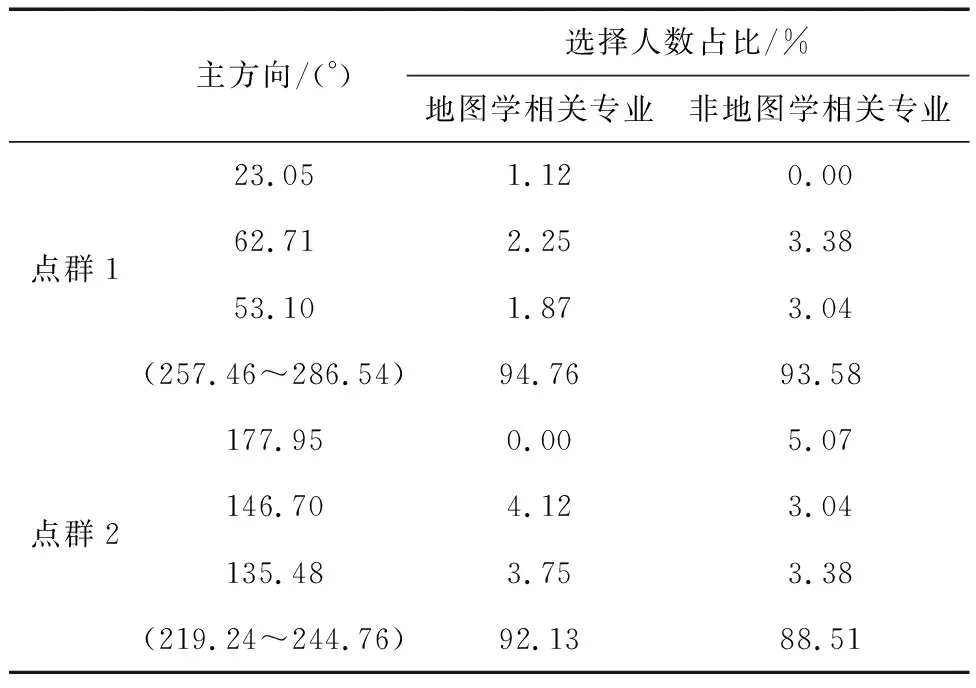
表2 点群主方向认知结果统计表

由表2的统计结果可知,地图学相关专业人员与非地图学相关专业人员对本文点群1实验结果的认同率分别为94.76%、93.58%,平均认同率为94.17%,对本文点群2实验结果的认同率分别为92.13%、88.51%,平均认同率为90.32%。不论是地图学相关专业人员还是非地图学相关专业人员,本结果的认同率远高于其它方法的认同率,利用本模型得到的定量计算结果更符合人们的空间认知习惯。

由表1数据可知,本文计算结果与已有方法计算结果相差较大。已有方法计算得到的点群1的主方向均未超过90°且最大仅为62.71°,而本计算结果为272°,已有方法与本方法的计算结果最大可相差209.29°,差别明显;已有方法计算得到的点群2的主方向计算结果均在90°～180°,而本计算结果为232°,已有方法与本方法的计算结果最大相差54.05°,计算结果仍存在较大差异。其原因如下:

1)已有的点群主方向计算方法利用凸壳、标准差椭圆等近似拟合点群的分布形态,在此基础上利用其直径、长轴代表点群分布主方向,没有顾及个别奇异点对其分布形态及直径、长轴的影响;本算法在锥形模型基础上构建方向玫瑰图判断点群方向关系,较好地维持了点群原始分布形态。

2)点群内部分布形态复杂,局部分布密度会影响点群的分布趋势,已有方法仅从点群整体分布出发来判断主方向,未考虑密度对其主方向判断的影响;本模型在构建过程中充分顾及到了分布密度的影响,得到的主方向计算结果更加符合人类认知。

4 结 论

本文综合考虑点群目标的分布形态及密度特征,借助16方向锥形模型构建方向玫瑰图,利用统计加权算法构建点群目标分布主方向的定量计算模型。实验结果表明,该模型较好地顾及了分布密度对点群目标空间分布主方向的影响,实现了符合人类认知的点群目标空间分布主方向定量描述。