基于DCC-GARCH-ΔCoVaR 模型的碳市场和煤炭市场风险溢出效应研究

郭 森，张凯文，祁 泽

（1. 华北电力大学 经济与管理学院, 北京 102206；2. 新能源电力与低碳发展研究北京市重点实验室（华北电力大学）, 北京 102206）

在能源结构转型和“双碳”目标背景下，我国正大力推动碳市场建设，以期利用市场机制推动碳减排步伐，实现经济绿色高质量发展。与此同时，通过对现有能源结构和经济发展趋势的判断，在现阶段及今后的一段时期，能源转型仍需立足以煤为主的基本国情。在此基本国情下的碳减排行动将催生煤炭价格和二氧化碳排放成本的较强关联关系。

目前，不同学者运用多种模型研究了碳市场中碳价的影响因素及风险溢出效应。辛姜（2018）等人利用向量自回归模型对不同条件下的碳价波动特征进行分析，结果显示碳价会受到金融市场和工业市场等的影响[1]。夏睿瞳（2018）利用AR-GARCH 模型对深圳市、北京市、上海市、天津市和武汉省碳排放交易市场的日收益率序列进行拟合，结果显示当期的收益率会受到内部冲击和外部冲击的双重影响，滞后期会对当前收益率造成影响，外部冲击会加大收益率的波动，使波动时间变长[2]。王心悦（2021）对我国五个试点地区的碳市场收益率和交易价格进行分析，结果显示不同地区的碳价和碳价收益率存在显著差别，但外部信息会对不同地区碳价造成影响，使得碳价发生波动[3]。周子璇（2021）利用ARIMA 模型探究碳价的特征，结果显示碳价呈非线性特征[4]。李菲菲等人（2019）利用GARCH 模型对六大碳市场的碳价数据的波动性进行分析，结果显示上海碳价波动幅度较大，北京的碳价收益率在极端情况下所面临的风险损失最大[5]。吴永等人（2021）构建ARMAGARCH（1,1）模型对试点地区的碳价进行分析，结果显示风险溢出效应仅存在于部分碳市场之间[6]。王喜平（2021）等人对欧洲碳市场对国内碳市场的风险溢出效应进行分析，结果显示欧洲碳市场对国内碳市场表现为正向的风险溢出[7]。张建文（2020）采用GARCH 模型和D-Y 溢出指数对我国地方碳市场之间的风险溢出效应进行刻画，结果显示碳市场的风险溢出效应具有时变性[8]。杨静（2021）采用BEKK-GARCH 和DCC-GARCH 模型分析资本市场和碳市场的风险溢出效应，指出资本市场与碳市场存在明显的风险溢出效应[9]。Bredin 等人研究经济环境、能源市场和气候环境等外部因素对欧洲碳价的影响，结果显示上述影响因素均会对欧盟的碳价产生有利影响[10]。Benz（2009）对欧洲碳市场进行分析，发现碳价格收益率具有高峰值，尾部较粗和波动性集聚等特征[11]。Alberola 等人（2008）则通过分析欧美碳价的影响因素，发现能源价格和温度能对欧美碳价造成影响[12]。Seifert（2008）通过构建欧盟碳现货价格的随机均衡模型来分析欧盟碳市场的影响因素，结果表明欧盟碳现货价格不受季节性影响[13]。Lin 和Chen（2019）分析北京碳市场、煤炭市场和资本市场间的动态关系和风险溢出效应，结果表明北京碳市场与煤炭市场间不存在风险溢出效应[14]。此外，Chang 和Ye（2019）对我国碳市场与能源市场的风险关系进行分析，指出能源市场与碳市场之间存在风险溢出效应[15]。Balcilar 等（2016）通过分析能源市场与欧洲碳市场之间的动态关系和风险溢出效应，发现能源市场与碳市场的关系存在明显的时效性，且风险溢出效应显著[16]。

上述文献中，一些学者分析了碳市场与能源市场之间的动态关系和风险溢出效应，研究表明碳市场和能源市场的动态关系和风险溢出效应会随碳市场建设地点、气候环境等外部因素发生变化。但上述研究主要是基于模型所估计出的相关系数显著性分析两个市场的风险溢出效应，缺乏对溢出的时变性和方向性的考察，并且上述文献主要从全国视角剖析了能源市场对碳市场的单向风险溢出关系，缺乏对地区之间异质性的分析，没有对不同地区碳市场和煤炭市场之间的双向风险溢出效应进行深入分析。因此，本文考虑我国碳市场发展现状及不同试点地区之间的经济结构、资源环境的异质性，运用DCC-GARCH-ΔCoVaR 模型对武汉、广东、深圳碳市场和煤炭市场的风险溢出效应进行研究，分析不同地区碳市场和煤炭市场之间的风险溢出时变性和方向性，从而为我国完善地区碳市场和能源市场机制提供政策参考，亦能够为市场主体规避碳市场与能源市场风险提供决策帮助。

一、研究设计

（一） DCC-GARCH 模型

DCC-GARCH 模型最早由Engle（2002）[17]提出，该模型用来描写两个变量在同一时刻的非线性关系，两个变量的DCC-GARCH 模型表达式为：

其中，Rt、 θ1、 θ2分别为动态条件相关系数矩阵、正的标量参数、负的标量参数，且θ1+θ2<1,qAB为t 时期变量A、B之间的协方差。

因此基于DCC-GARCH（1,1）模型，两个变量的动态相关系数ρAB,t的计算公式为：

动态条件相关系数ρAB,t越大，表示风险溢出效应的程度越高。即当其中一个变量所代表的市场价格发生大幅度波动，所对应的另一个市场的价格波动幅度也会增大。

（二） CoVaR 模型

通常VaR 方法主要用来衡量在某一置信水平下，单个资产或机构所面临的最大损失，但是该方法只能用来衡量单个资产或机构内部的风险，无法衡量外部资产或机构波动所造成的系统性风险。系统性风险的主要特征为：1.一个极端事件对整个系统造成冲击，2.该极端事件也让第三方承担额外的成本。因此系统性风险的典型特征表现为风险存在溢出性和传染性[18]。

CoVaR 方法对VaR 方法进行改进，可以用来衡量系统性金融风险，CoVaR 表示在给定的时间和置信水平下，变量A发生损失时，变量B所面临的最大潜在风险损失。因此当变量A的所面临风险损失为VaRqA时，变量B的所面临最大风险潜在损失为：

式中CoVaRqBA为变量B所面临的最大潜在风险损失，1-q 为置信水平，在此基础上构建变量 A 对变量 B 的ΔCoVaR 模型：

（三） DCC-GARCH-ΔCoVaR 模型

根据王周伟（2015）[19]对VaR 的定义，单个资产的VaR 计算式为:

由式（1）-（9）可推导出基于DCC-GARCH 模型的变量A对变量B的风险溢出效应值：

二、实证分析

（一） 数据选取和处理

我国现有8 个碳市场试点地区，即北京、上海、天津、重庆、湖北、广东、福建和深圳八省市地区，其中重庆、福建、天津和上海的碳交易量小，碳市场不活跃，在一段时间处于暂停交易阶段，不具备实证的条件，将以上四个市场剔除。北京碳排放市场虽然成立时间早，但是北京市在2016 年起就开始限制煤炭的使用，煤炭对碳排放市场的溢出效应无法很好地反映，且北京碳市场交易量小，交易不活跃。因此本文选取成立时间长、交易量大的武汉碳市场、深圳碳市场和广东碳市场作为研究对象。

武汉碳市场在三个市场中最晚成立，相关数据从2014 年5 月开始，本文选取2014 年5 月5 日到2021 年10 月14 日的武汉碳价收盘价格、广东碳价收盘价格、深圳碳价收盘价格以及动力煤价格的日度数据，删除日期不重合的数据，得到有效数据5372 个。对有效数据进行对数化处理，所得到的数据不仅可以用来衡量收益率，还消除了异方差问题。其中武汉碳价、深圳碳价、广东碳价来自碳排放交易网（http://www.tanpaifang.com/），煤炭价格数据来自Wind 数据库。

对相关数据进行定义，R1表示武汉碳价收益率序列，R2表示广东碳价收益率序列，R3表示深圳碳价收益率序列，R4表示煤炭价格收益率序列。

（二） 数据的描述性统计和ADF 检验

由表1 可知，武汉、广东、深圳的碳价收益率序列以及煤炭价格收益率序列的J-B 统计量p 值都为0，说明4 个市场的收益率序列都不服从正态分布。从标准差来看，深圳碳价收益率的数值最大，为0.388，说明深圳的碳价收益率波动及对应风险相对于其他三个市场大。武汉、广东、深圳的碳价收益率序列以及煤炭价格收益率序列在99%的置信度水平下都是显著的，说明3 个碳市场和煤炭市场的收益率均为平稳序列，可以进行后续ARCH 检验。

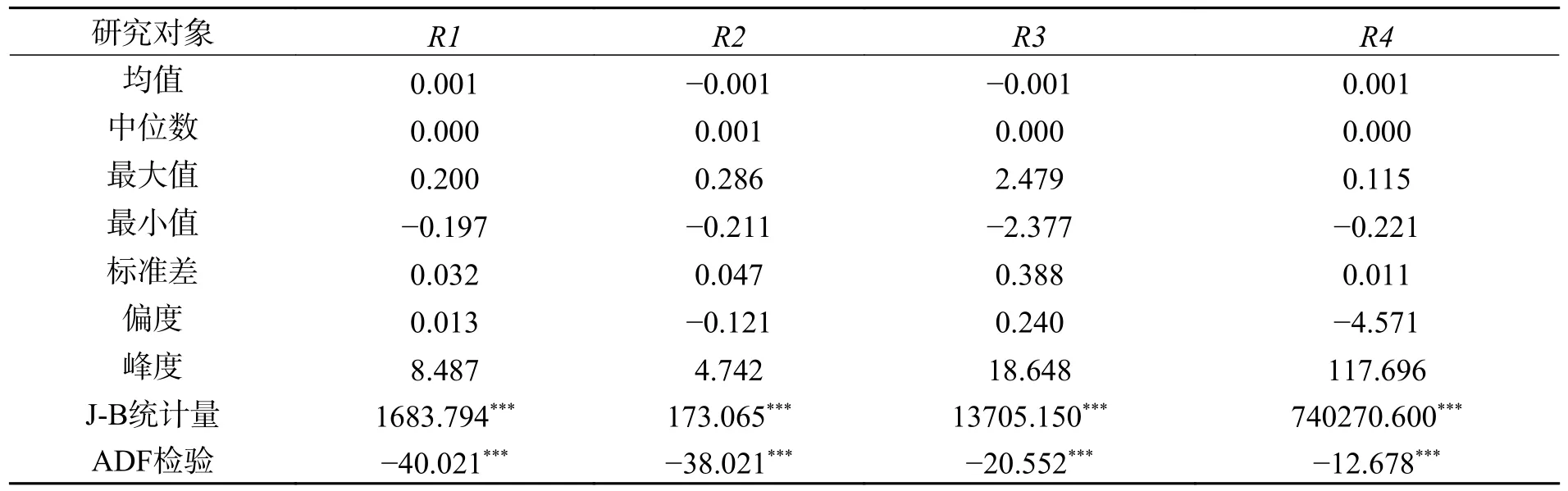
表1 描述性统计和ADF 检验

（三） 自相关检验与ARCH 检验

对四个收益率序列进行自相关性检验。通过检验可知，R1、R3、R4存在自相关性，R2不存在自相关性。因此对上述变量建立多个ARMA 模型，并根据AIC 值和SC 值确定各变量的最终方程，并对最终方程进行ARCH 检验，检验结果如下表2 所示：

表2 ARCH 检验表

可以发现，R1，R2，R3，R4的F 统计量在99%的水平下显著，说明对各变量所建立的模型存在ARCH 效应，进而对各变量构建GARCH 模型。

（四） GARCH 模型构建

由上文可知，四个收益率存在ARCH 效应，考虑4 个市场中可能存在非对称效应。因此分别对4 个市场构建GARCH 模型、TGARCH 模型、EGARCH 模型，结果如表3 所示：

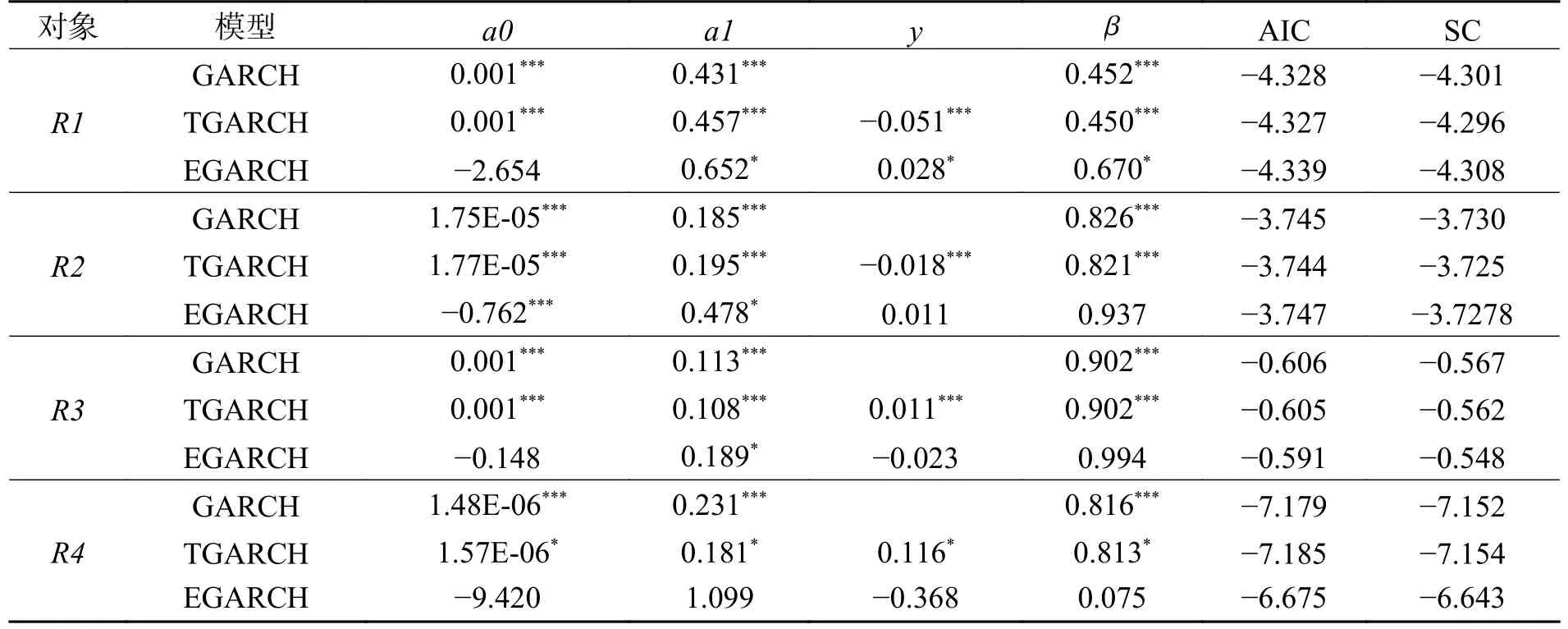
表3 模型拟合表

其中， α0表示常数项， α1表示ARCH 项系数，在经济学中解释为外部冲击对条件方差的影响，反映市场对外部冲击的敏感程度； β表示GARCH 项系数，在经济学中解释为内部冲击对条件方差的影响，反映了收益率波动的持续性； γ表示非对称项系数，在经济学中表示杠杆效应，由表3 可知：R1，R2，R3，R4的 γ均不为0，各变量均存在非对称效应。综合模型系数、AIC 和SC 信息准则，对R1，R2和R3构建TGARCH 模型，对R4构建GARCH 模型。

α1数值显示，R1>R2>R3>R4，说四个市场中武汉碳市场对新信息最敏感，广东和深圳次之，煤炭市场对新信息的反映最为迟钝。 β数值显示，R3>R2>R4>R1，说明市场冲击对深圳碳市场造成的冲击最为持久。R1和R2的 γ都大于0，说明武汉碳市场和广东碳市场存在杠杆效应，也就是说当市场中存在新消息时，新消息会对这两个市场造成正向冲击，且该冲击还会随着杠杆效应不断加大。R3和R4的 γ都小于0，说明非对称效应使得市场波动减小，当有新消息存在时，会使得深圳碳市场和煤炭市场的波动减小。

（一） 模型结果和分析

1. 武汉碳市场和煤炭市场

利用R1和R4的GARCH 模型所得出的残差序列进行DCC-GARCH 分析，从而得到广东碳市场和煤炭市场之间的动态相关系数、风险溢出关系以及风险溢出值，动态相关系数如图1 所示。

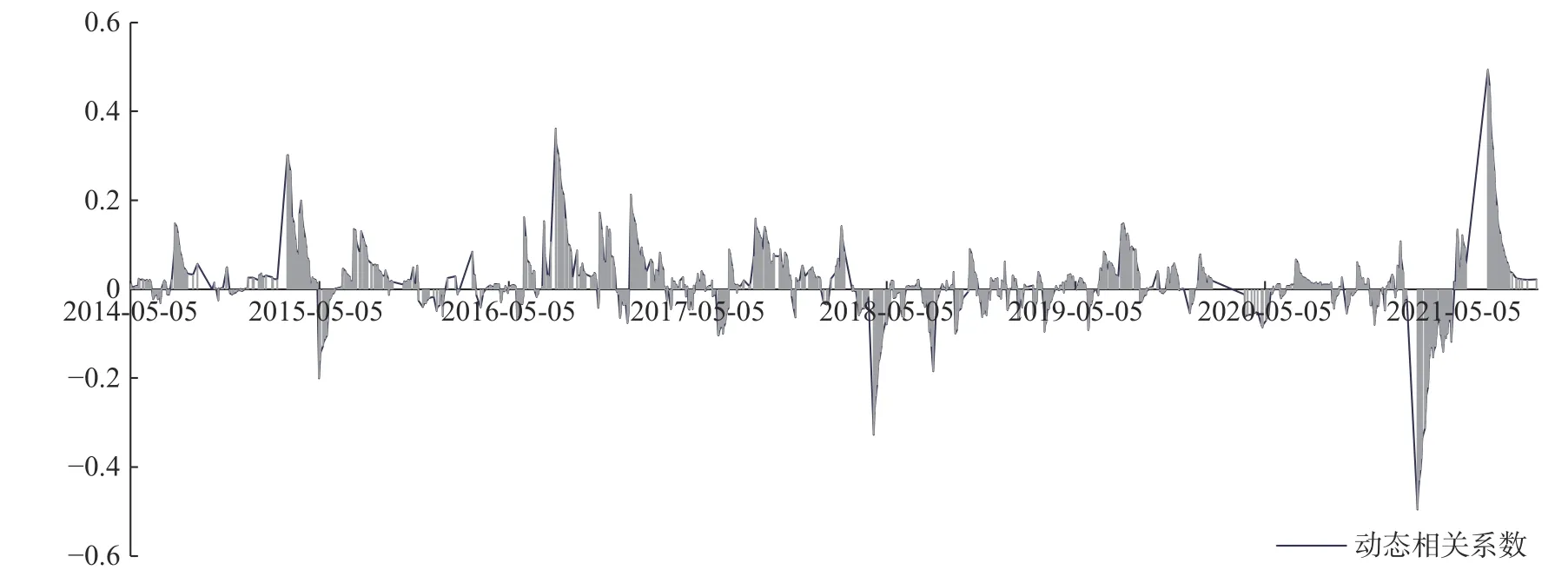
图1 R4 与R1 的动态相关系数

结合图1 结果从波动范围进行分析，2014—2020 年R1和R4的动态相关系数在-0.2 与0.2 范围内波动，到了2021 年动态相关系数波动幅度增大，在-0.4 与0.4 之间波动；从动态方向进行分析，2014 年—2020 年R1与R4总体呈现出正向的动态关系。

当煤价出现剧烈波动时，两个市场的相关系数随之发生剧烈波动，煤炭市场通过电力企业这一中介因素对碳市场产生影响。图2 显示武汉碳价和煤炭两个市场的风险溢出关系。

图2 武汉碳市场与煤炭市场的风险溢出关系

从表4 和图2 可以看出，R4的CoVaR 的值比R1的值大，说明煤炭价格的条件风险价值比武汉碳交易价格的条件风险价值大。从两个市场的△CoVaR 值和△CoVaR 图形来看，煤价市场对武汉碳价的风险溢出大于武汉碳价对煤价市场的风险溢出。煤炭市场在整个电力生产行业中处于上游市场，同时由于武汉以重工业为经济支柱，对煤炭以及电力的需求量大，碳排放量高，煤炭市场在“炭-电-碳”的传导途径中占比大，煤炭市场的风险通过该传导路径直接影响碳市场。

表4 条件风险价值、边际风险溢出值

从时间维度来看，煤炭价格在2015 年和2016 年对武汉碳市场有着很大的风险溢出，在这两个时间点，煤价都出现了很强的价格波动，对发电企业的发电量造成了直接冲击进而影响碳价波动。虽然武汉的碳市场已经成为全国最大的碳市场，但此时由于武汉的碳市场建设才两年，制度建设不健全，国内主流对碳排放不够重视，使得碳市场无法对煤炭市场造成反向冲击。到了2021 年，随着“双碳”目标的提出，国家进一步重视绿色建设，同时经过5 年的发展，武汉碳市场交易机制不断完善，交易量持续上涨，碳市场对煤炭市场造成反向风险冲击。

2. 广东碳市场和煤炭市场

利用R2和R4的GARCH 模型所得出的残差序列进行DCC-GARCH 分析，从而得到广东碳市场和煤炭市场之间的动态相关系数、风险溢出关系以及风险溢出值，动态相关系数如图3 所示。

图3 R2 与R4 的动态相关系数

结合图3 结果从波动范围进行分析，2014—2020 年R4和R1的动态相关系数在0 至-0.6 范围内波动；从动态方向进行分析，2014—2020 年R1与R4总体呈现出负向的动态关系，在2015 年5 月出现不显著的正向动态关系。

总体而言，广东碳价和煤炭两个市场表现出负向的动态相关关系，当煤价出现剧烈波动时，两个市场的相关系数随之发生剧烈波动。图4 显示广东碳价和煤炭两个市场的风险溢出关系。

图4 广东碳市场和煤炭市场的风险溢出水平

从表5 和图4 可以看出，R4的CoVaR 的值比R2的值大，说明煤炭价格的条件风险价值比广东碳交易价格的条件风险价值大，从两个市场的△CoVaR 值和△CoVaR 图形来看，煤炭市场对广东碳价的风险溢出大于广东碳价对煤价市场的风险溢出。

表5 条件风险价值、边际风险溢出值

从时间维度上看，2014 年煤价对广东碳市场有着很大的风险溢出，广东省的碳排放价格在2014 年 成 立 之 初 出 现 过 暴 跌，由2014 年5 月5 日 的66.8 元 下 跌 到2014 年10 月16 日的25.65 元。2014 年，由于广东省碳市场处于起步阶段，为实现碳履约的正常进行，广东碳市场采用3%的有偿配额和97%的无偿配额机制的碳配额分配机制，企业所持有的碳排放配额较宽松，企业缺乏交易需求，导致广东碳市场800 万吨碳配额没能全部竞拍出去，碳价格不断下跌，此后广东省的碳排放价格在30 元范围波动。在煤价正常波动范围内，广东碳市场本身机制使得两个市场在期初呈现负的溢出效应。到2021 年，随着市场机制不断完善，广东碳市场能对上游煤价市场产生影响，对煤价造成反向的风险溢出。

3. 深圳碳市场和煤炭市场

利用R3和R4的GARCH 模型所得出的残差序列进行DCC-GARCH 分析，从而得到深圳碳市场和煤炭市场之间的动态相关系数、风险溢出关系以及风险溢出值，动态相关系数如图5 所示。根据图5 结果从波动范围进行分析，2014—2020 年R3和R4的动态相关系数在-0.15 与-0.05 范围内波动，到了2021 年动态相关系数波动幅度减小，在0.5 范围内波动；从动态方向进行分析，2014—2020 年R3与R4呈现出负向的动态关系，在2020 年5 月—2021年呈现出正向的动态关系。

图5 R3 与R4 的动态相关系数

图6 显示深圳碳价和煤炭两个市场的风险溢出关系。

图6 深圳碳市场与煤炭市场的风险溢出水平

从表6 和图6 可以看出，R4的CoVaR 的值比R3的值大，说明煤炭价格条件风险价值比深圳碳交易权的条件风险价值大。从两个市场的△CoVaR 值和△CoVaR 图形来看，两个市场在样本期间内大部分呈现负向的风险溢出效应。就具体数值而言，煤炭价格对深圳碳价的风险溢出程度大于后者对前者的风险溢出程度。

表6 条件风险价值、边际风险溢出值

从时间轴上来看，在2019 年5 月份，煤炭市场对深圳碳排放市场的风险溢出效应达到最大值。在动态相关系数图中，两个市场的动态相关系数也达到了最大值，其中2020 年煤炭市场对深圳碳市场的溢出效应变为正值，与动态相关系数图变动一致。

三、结论与建议

基于上文的实证分析，本文主要得出以下结论：

（1）从单个市场角度来看，武汉碳市场对外部信息最敏感，广东和深圳次之，煤炭市场对外部信息的反映最为迟钝。市场冲击对深圳碳市场造成的冲击最为持久，深圳碳市场需要长时间去吸收冲击所造成的影响。武汉碳市场和广东碳市场存在杠杆效应，当市场出现一个利好消息时，会对这两个市场造成正向冲击，且这个冲击会随着杠杆效应不断加大。深圳碳市场和煤炭市场存在反杠杆效应，当有外部信息冲击时，会使得两个市场的波动减小。

（2）从碳市场和煤炭市场的风险溢出角度而言，碳市场在建设初期，由于市场机制的不完善和交易量的不活跃，两个市场之间主要表现为煤炭市场对碳市场的风险溢出效应。随着碳市场的不断完善，碳市场对煤炭市场造成风险溢出，此时碳市场和煤炭市场之间存在双向的风险溢出效应。与此同时，由于三个地区的电力结构不同，也会对风险溢出效应的方向造成不同影响，相对于煤价的波动溢出对武汉碳市场的正向冲击，广东碳市场和深圳碳市场由于存在“西电东送”政策，可以从外省获得大量电力，煤价的波动溢出会对碳价造成负向冲击。

综上，由于碳价市场和煤炭市场之间具有显著的风险溢出效应，以及两个市场的溢出水平和溢出方向存在着强烈的区域性变化，这些因素均不利于有效防范碳价市场以及煤炭市场的价格风险，为此本文提出以下建议：

（1）根据建立全国统一碳市场的实际需求，综合考虑并合理协调各区域差异，以形成多元贸易体系

从上述结论可以看出不同的碳市场对信息的敏感程度不同，相同的信息可能会对不同的地方碳市场造成不同的影响，煤炭市场会对各个区域的碳市场会产生不同的风险溢出效应。因此，在我国建立统一碳市场制度背景下，因地制宜，综合考量各地区的产业结构、经济环境、人口比例等外部因素，结合该地区的碳市场的碳配额分配方法，选择多样化的交易制度，搭建碳现货、碳期货等碳金融工具，通过套期保值等市场化手段减少外部信息所造成的碳市场价格波动，合理规避碳风险。此外,政府部门在碳市场的制度设计和运行管理过程中，还须加强宏观调控，避免过度投机等市场内部行为造成碳价剧烈波动，通过市场监管、定期抽查企业碳排放量等行政手段降低碳价波动风险，并维护碳价的在合理范围波动。

（2）完善我国碳市场自身风险监测机制

从本文研究结论可以看出，碳市场成立初期由于市场机制的不完善和交易量的不活跃，两个市场之间主要表现为煤炭市场对碳市场的风险溢出效应。因此，在全国统一碳市场建立初期需要构建相应的风险预警制度，以减少煤炭市场对碳市场产生的单方向性风险溢出。一方面，全国统一碳市场监管者必须对可能造成碳市场价格剧烈波动的因素进行防范，避免碳市场价格剧烈波动，另一方面，在建立全国统一碳交易市场时，也必须充分考虑煤炭价格波动等干扰风险对区域减排成本所产生的不良影响，并提出有效合理可行的风险监控方法。