基于XGBoost-神经网络的建筑负荷预测模型构建

魏东, 杨洁婷, 韩少然, 朱准

(1.北京建筑大学电气与信息工程学院, 北京 100044; 2.建筑大数据智能处理方法研究北京市重点实验室, 北京 100044;3.北京京诚瑞达电气工程技术有限公司, 北京 100176; 4.北京城建设计发展集团股份有限公司, 北京 100034)

公共建筑集中式空调系统能耗约占建筑总能耗的40%[1],而准确的负荷预测能够为系统优化控制策略提供理论依据,是实现空调系统按需供冷、节能运行的前提条件。

目前常用的预测方法有时间序列、集成学习和人工神经网络等。集中式空调系统体积庞大、组成复杂,且含有冷水机组、水泵、风机等非线性设备,因此具有较强的非线性、大滞后、强耦合特性。时间序列法根据统计学原理进行建模,适用于线性关系和较简单的非线性映射[2];集成学习模型中子学习器的多样性与求得解的准确性或鲁棒性之间往往存在冲突,需频繁地调整子学习器的结构参数,或需引入进化算法[3],不易移植;由于人工神经网络具有良好的移植性,且已证实3层前馈神经网络可以拟合任意非线性函数,并对非线性系统有较强的鲁棒性[4],因此采用3层前馈神经网络实现建筑负荷预测。

负荷预测需要利用现场温度、湿度、流量等多种传感器采集的数据对模型进行训练实现,现场运行数据存储量大、维度高,且易受到现场复杂环境干扰。大规模高维数据存在多重共线性问题,易导致解空间不稳定,同时高维空间样本具有稀疏性[5],会造成模型难以找到数据特征,从而降低模型泛化能力,利用特征工程可以解决该问题。特征降维属于特征工程的一种[6],包括特征提取和特征选择两种方式。有效的特征降维方法可以确保特征属性之间的相互独立性,能够解决模型过拟合问题,从而提升其泛化能力。闫秀英等[7]利用主成分分析法进行空调系统的特征提取,采用优化极限学习机建立负荷预测模型。主成分分析法属于特征提取方法,该方法主成分的累计贡献率确定具有主观性,而且被提取的主成分很难给出符合实际背景和意义的解释[8],使工程人员难以理解现有特征的价值。胡瑞等[9]利用随机森林模型进行特征选择,然后构建了决策树算法、随机森林、线性回归和贝叶斯岭回归4种模型,分别预测高熵合金相稳定性,实验证明随机森林的预测精度最高,且进行特征选择可对网络输入进行修剪,消除冗余计算,从而提高模型的泛化能力。特征选择方法在实现特征降维的同时,可以保留所选择特征的完整物理含义,更便于研究人员充分理解负荷与其影响因素之间的关系。但是,对于随机森林算法来说,单棵决策树对数据的变化非常敏感,对某些存在噪声的数据建模时很容易出现过拟合,进而影响特征选择的效果,逐渐添加决策树数目时可减少出现过拟合的情况发生,但计算量会随之增加。Chen等[10]提出的极限梯度提升(extreme gradient boosting, XGBoost)对随机森林算法[11]进行了改进,该方法若发现某节点的增益最小,将停止将树构建到更大的深度,从而能够有效避免过拟合发生;此外,相对于随机森林算法,XGBoost能进行特征的并行化处理,可减少计算量。因此采用XGBoost特征选择方法实现特征降维。

另一方面,由于训练样本不可避免地包含误差,若神经网络结构冗余,在网络训练后期,这些误差会影响神经网络的训练收敛方向,从而易造成全局最优点偏离,降低模型泛化能力。邵恩泽等[12]对于输入节点和隐层节点分别采用基于灵敏度和基于相关度的剪枝方法,以降低网络结构复杂度。实验结果证明了剪枝后的神经网络泛化能力更强。如果在神经网络训练目标函数中引入表示网络结构复杂性的惩罚项,通过贝叶斯正规化方法[13]进行模型训练,则既可使网络尽可能地拟合训练样本数据,又能通过在训练优化过程中降低网络结构的复杂性,达到避免模型过拟合的目的。魏东等[14]利用神经网络建立空调负荷预测模型,采用贝叶斯正则化算法对模型进行训练,提升了其泛化能力。但是,该研究基于主观经验确定模型的输入变量,有可能造成重要特征信息丢失。

为解决上述问题,现利用XGBoost对原始数据集进行特征选择,再采用贝叶斯正则化方法训练神经网络,构建负荷预测模型。针对某商业建筑空调系统负荷预测实验结果验证所提方法的有效性。

1 研究对象及运行数据采集

以商业建筑空调系统为研究对象,该建筑位于中国西南地区,面积为41 000 m2,建筑高度为31.4 m,共有7层,包括地上五层和地下二层。地下二层为车库,地下一层为超市,地上一～四层为商业区域,五层和夹层为餐饮区及电影院。冷冻站、配电房、热水机房、超市部分空调通风设备设置在地下室内。

为了实现负荷预测,配置了相关室内和室外传感器设备以采集数据。数据采集系统采用MODBUS通信协议,通过标准RS485接口与控制中心计算机连接,实现信息交互。所配置的室内传感器设备包括温湿度传感器、电磁式流量传感器、水温传感器、压力传感器等,用于监测冷却水供/回水流量、压力,以及各制冷机供/回水冷冻水流量等变量;建筑顶楼设有小型自动气象站,配置了相关室外传感器设备,包括单翼风向传感器、风杯风速传感器、热电堆式辐射传感器、铂电阻温度传感器、湿敏电容湿度传感器,现场检测室外温/湿度、风向、风速、太阳辐射等气象参数。部分传感器设备如图1所示,部分传感器设备信息如表1所示。

表1 传感器设备信息Table 1 Sensor equipment information

图1 部分传感器设备Fig.1 Some sensor equipment

数据采集时间为7月19日—9月12日,采样周期为30 s,共采集到50个维度的特征样本数据,包括:①地下一层至地上五层室内温度及湿度;②冷水机组、冷却水泵、冷冻水泵、冷却塔耗电量;③冷却水供回/水流量、压力,冷冻水供回/水流量等系统运行数据;④室外温度、湿度、风速、风向、太阳辐射照度等气象数据。部分数据如表2所示。

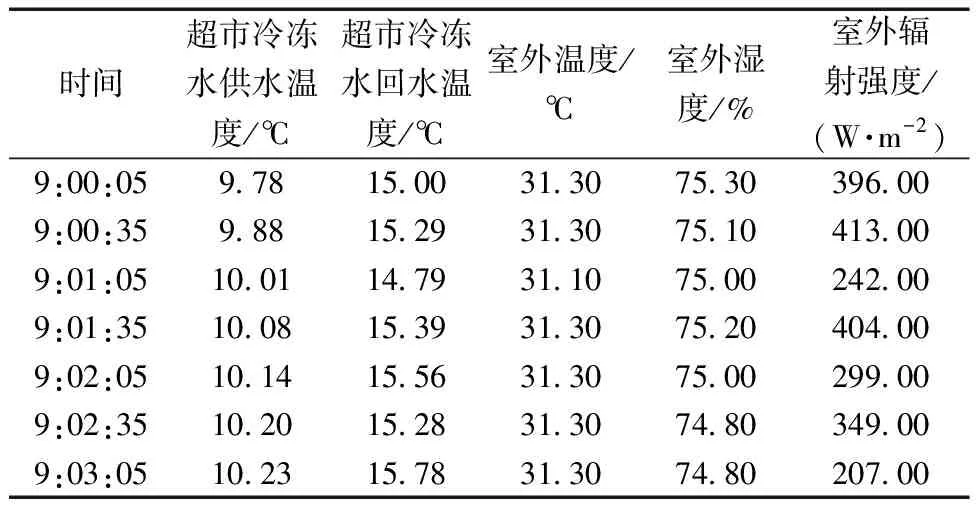
表2 部分样本数据Table 2 Partial sample data

2 特征筛选

如前所述,采用XGBoost算法进行特征选择。XGBoost是由若干以决策树为基学习器组成的强学习器,其可表示为

(1)

模型训练的性能指标为

(2)

(3)

(4)

模型训练时,每次迭代即添加一棵新树,第t次迭代的目标函数为

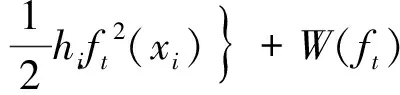
(5)

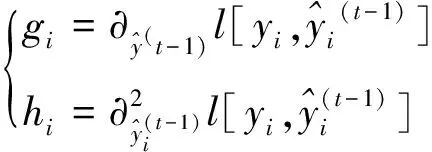
(6)

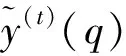
(7)

(8)

式中:j为叶子节点;Ij为当前节点的实例集。

XGBoost算法的迭代过程中,权重和增益两个参数反映了某个特征与预测目标的相关性[15]。权重表示某特征出现的次数,该特征信息增益总和除以出现的次数即为增益。增益的计算公式为

(9)

式(9)中:下角标L、R分别为左子树和右子树。

3 负荷预测

采用3层前馈神经网络构建负荷预测模型。为提升神经网络泛化能力,需要优化网络结构复杂性,即寻找最优的网络参数。利用贝叶斯理论框架[16]将模型参数视为不确定参数,使用显式的概率分布假设对模型进行分析和推断,然后,根据融入先验分布的假设和依据,基于后验分布的贝叶斯推理得出最优化参数。

传统神经网络将均方误差(mean squared error,MSE)作为误差性能函数,即

(10)

通过贝叶斯正则化方法修正性能函数,即在性能函数上加上正则化项为

(11)

式(11)中:M为网络的权值数量;wj为网络的第j个权值。

修正后的误差性能函数为

J=αJW+βJD

(12)

式(12)中:α、β为正则化参数,可控制JW与JD在网络中的占比。求取超参数α、β,需要求出后验分布,公式为

(13)

式(13)中:H为网络结构;D={x(N),d(N)}为数据集;p(D|w,β,H)为似然函数;p(D|α,β,H)为归一化因子;p(α,β|H)为先验分布。

因为p(D|H)与α、β无关,因此问题就转化为对最大似然函数p(D|α,β,H)的求解。

通过贝叶斯推理,有

(14)

式(14)中:ZJ(α,β)、zD(β)[17]和zW(α)均为归一化因子,求解公式为

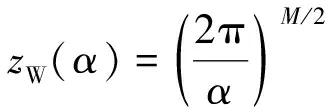
(15)

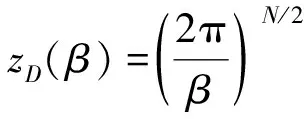
(16)

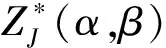
∇∇J(wMP)(w-wMP)]dw

=(2π)M/2{det[∇∇J(wMP)]}-1/2×

exp[-J(wMP)]

(17)

将式(15)～式(17)代入式(14),并取对数,可得

lnp(D|α,β,H)=-αJW(wMP)-βJD(wMP)-

(18)

将式(18)分别对α、β求偏导,并令其等于0,可得

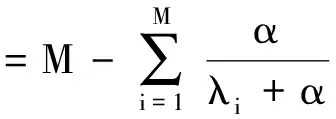
(19)

=N-γ

(20)

由式(19)和式(20),可求得

(21)

式(21)中:下标MP代表后验概率最大时的状态;γ为有效参数的数量,γ=m-2αtr(H-1),H为J的Hessian矩阵,H=α∇2JW+β∇2JD。

以贝叶斯正则化方法作为神经网络训练算法时,需要判断α、β的收敛性,若收敛,则训练完成;若不收敛,需重新计算γ,从而更新α、β。基于贝叶斯正则化方法的神经网络训练步骤如下。

步骤1初始化超参数α、β和神经网络权值Wj,此处取α=0,β=1。

步骤2基于Levenberg-Marquardt(L-M)算法最小化修正后的误差性能函数J。

步骤3求解J的Hessian矩阵,计算γ的值。

步骤4由式(21)计算超参数α、β的新估计值。

步骤5重复执行步骤2～步骤4,直至α、β收敛。

4 实验研究

4.1 数据处理

在完成数据采集后,通过对数据进行可视化分析,发现数据中明显存在较多尖峰脉冲和随机扰动,这是因为温度、湿度、流量等变量的检测装置易受到静电、电磁辐射、磁场耦合、直接传输等干扰影响;此外,空调系统现场安装有多台制冷机、水泵、风机等大功率设备,大功率感性负载的启停会使电网产生尖峰脉冲干扰。因此应用中位值滑动平均滤波法对特征样本数据进行滤波处理,该算法中采样数据的数目N取值范围一般为[3,14],这里取N=10。

以部分室外空气湿度数据滤波为例展示滤波效果,如图2所示。

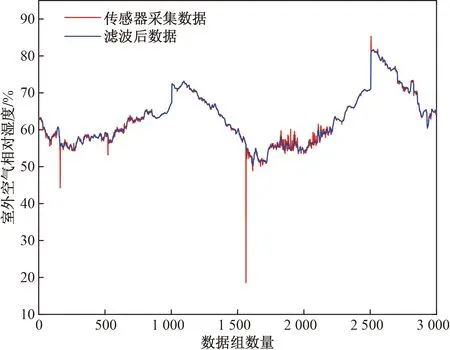
图2 滤波前后数据对比Fig.2 Comparison of data before and after filtering

由图2可见,经中位值平均滤波后,一些偶然出现的脉冲干扰和异常信号被滤除。

4.2 特征筛选实验分析

利用XGBoost对所采集的50维特征数据与负荷之间的相关性进行排序,排序结果如图3所示。

f0～f49表示特征变量编号

采用平均绝对百分比误差(mean absolute percentage error,MAPE)对样本数据特征维数与模型预测性能之间的关系进行检验。MAPE计算方法为

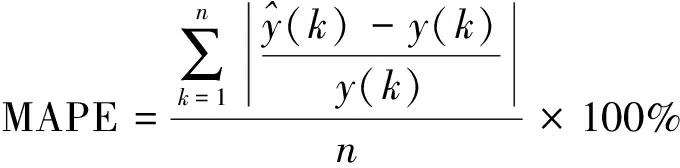
(22)

得到特征变量数量与MAPE的关系如图4所示。

图4 不同特征维度下的程序运行时间和MAPE Fig.4 Program runtime and MAPE in different feature dimensions

由图4可知,当选择特征个数为30时,MAPE最低,为10.25%,模型运行时间为0.76 s,在可接受范围内,因此选择此30个特征变量作为筛选后特征数据,如表3所示,其中温度号码代表安装在不同位置的温度传感器所采集数据。

表3 筛选后的特征变量Table 3 Feature variables after selection

4.3 前馈神经网络结构与参数实验

以筛选后的30维特征数据为输入搭建前馈神经网络预测模型,通过经验公式[式(23)]获取隐层的节点数取值范围为[8,17]。

(23)

式(23)中:h为输入层节点数;l为输出层节点数;ε为隐含层节点数;θ为范围1～10的调节常数,其余变量同上。

神经网络的泛化能力对初始权值(阈值)也很敏感,采用Nguyen-Widrow算法生成初始权值和阈值[18],然后以MSE最低为目标进行实验,最终确定隐含层节点数为9,结果如表4所示。

表4 特征筛选后隐层神经元数目实验结果Table 4 Experimental results on the number of hidden layer neurons after feature selection

学习率是神经网络重要的超参数。默认的学习率取值策略是使用较小的学习率,因此确定学习率取值范围为[0.001,1]。在确定隐层神经元数目为9的条件下,以MSE最低为目标进行一系列实验,确定神经网络学习率为0.1,结果如表5所示。

表5 特征筛选后学习率实验结果Table 5 Experimental results of learning rate after feature selection

为进行对比,同时以筛选前的50维特征数据为模型输入,采取上述方法确定隐层神经元数目为12,神经网络学习率为0.2。

4.4 特征筛选前后负荷预测实验

特征筛选前后神经网络模型预测效果对比如图5所示,为直观体现特征筛选对预测精度的影响,截图第70～75组测试数据如图6所示,特征筛选前后神经网络模型的MSE下降曲线如图7所示。由图5和图6可知,特征筛选后神经网络模型较筛选前具有更好的拟合效果;分析图7可知,未经过特征

图5 特征筛选前后神经网络模型预测效果Fig.5 The prediction effect of the neural network model before and after feature selection

图6 第70～75组测试数据预测效果Fig.6 The prediction effect of the 70th to 75th group of test data

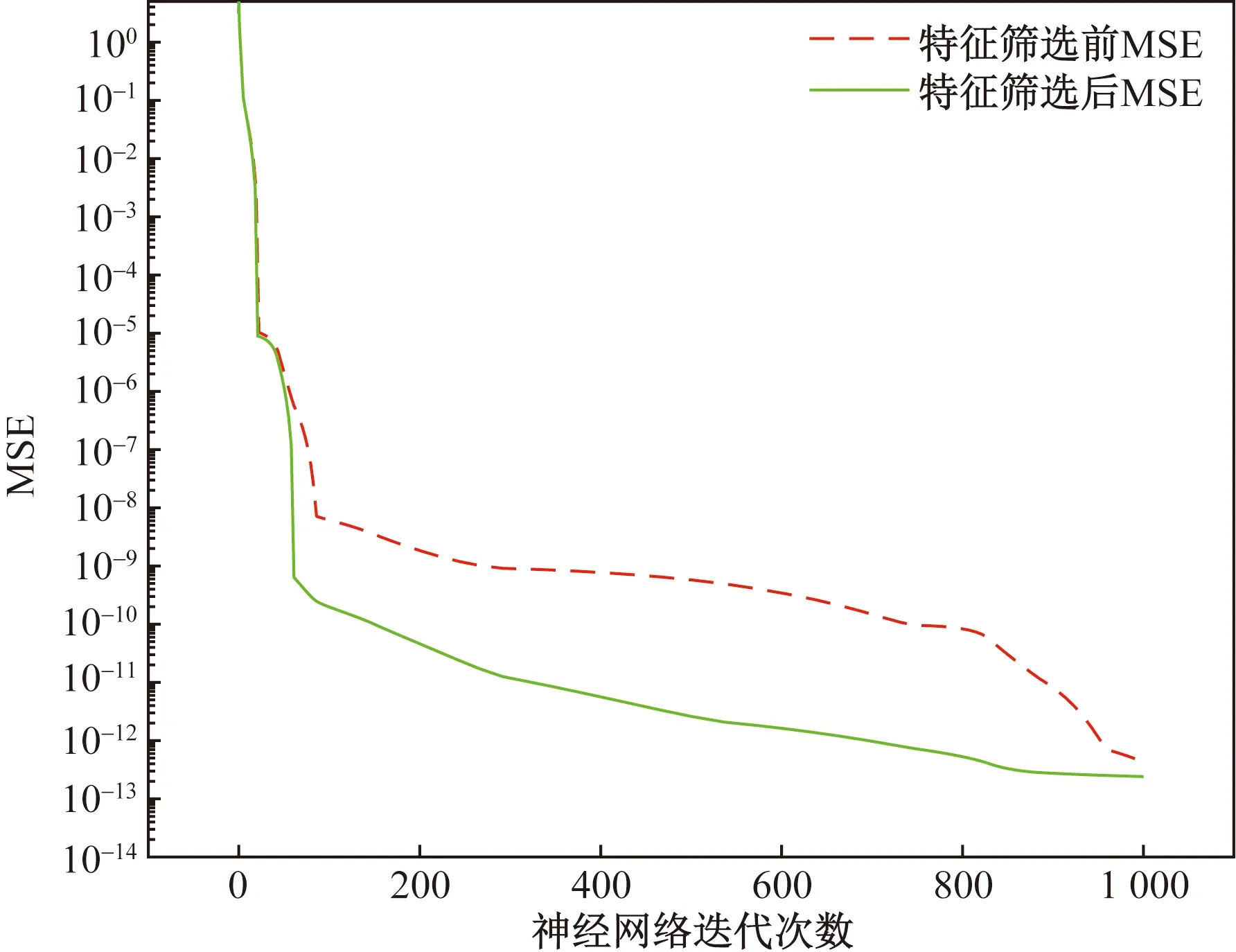
图7 神经网络模型MSE下降曲线Fig.7 MSE decline curve of neural network model

筛选的神经网络模型MSE分别在第30次迭代和第813次迭代时发生两次大幅度下降,最终MSE为4.25×10-13;经过特征筛选的神经网络模型MSE在第30次迭代时发生大幅度下降,随后缓慢下降,最终MSE为2.41×10-13;对比可知,神经网络模型经过特征筛选后,较特征筛选前MSE降低了43.29%。

4.5 泛化能力对比实验

为了验证神经网络负荷预测模型性能,首先对所采集的710组特征数据进行数字滤波,并利用XGBoost特征筛选层进行特征选择,然后随机选取497(70%)组数据作为训练数据,其余213(30%)组数据作为验证数据。对于训练数据,分别利用贝叶斯正则化方法和L-M算法对神经网络进行训练,在相同条件下用213组验证数据对这两个网络模型分别进行5次测试,将均方根误差(root mean squared error,RMSE)和MAPE作为性能指标。RMSE计算公式为

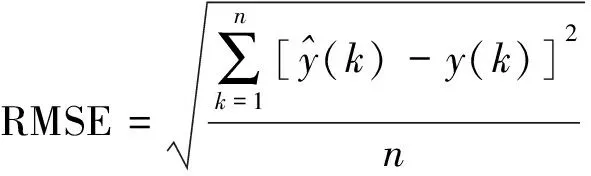
(24)

采用贝叶斯正则化和L-M算法训练的神经网络5次实验结果和统计结果分别如表6、表7所示。

表6 泛化能力对比实验结果Table 6 Comparison experimental results of generalization ability

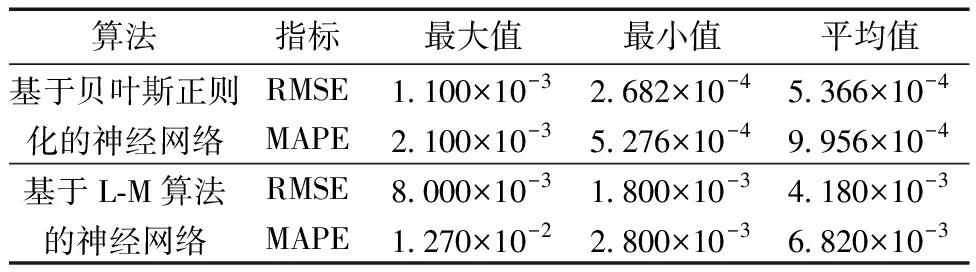
表7 泛化能力实验统计结果Table 7 Experimental statistical results of generalization ability

从表6中可以看出,5次实验下,采用贝叶斯正则化算法训练的神经网络RMSE在2.682×10-4～1.100×10-3变化,采用L-M算法训练的神经网络RMSE在1.800×10-3～8.000×10-3变化,对两者的MAPE分析同上。从表7可以看出,对比采用贝叶斯正则化和L-M算法训练的神经网络,前者的RMSE和MAPE的最大值、最小值以及平均值均低于后者。5次试验下前者RMSE的最大值为1.100×10-3,与后者RMSE的最小值1.800×10-3相比降低了7.000×10-4,MAPE亦然。与后者相比,前者的RMSE和MAPE平均值分别减少了87.08%、85.33%,这充分证明了采用贝叶斯正则化方法训练的神经网络泛化能力更强,预测精度更好。

5 结论

提出了一种基于XGBoost-神经网络的公共建筑负荷特征筛选及预测方法。特征筛选层利用XGBoost方法对滤波后的数据进行训练确定最优特征子集,以提升模型泛化能力,避免大规模高维数据输入导致模型训练时间过长、易陷入局部最优,并可能导致振荡的情况发生。负荷预测层采用3层前馈神经网络实现,在网络目标函数中引入表示网络结构复杂性的惩罚项,以使网络在尽可能拟合训练样本数据的同时,降低网络结构复杂性,达到提升模型泛化能力的目的。利用某商业建筑传感器所采集的数据构建负荷预测模型,通过实验结果可得到以下结论。

(1)经过特征选择后的神经网络预测模型较特征选择前MSE降低了43.29%,有效减少了高维特征数据对模型预测精度的影响。

(2)对采用贝叶斯正则化方法和L-M算法训练的神经网络负荷预测模型进行泛化能力实验对比,5次试验下前者的RMSE和MAPE平均值分别降低87.08%、85.33%,说明前者的泛化能力优于后者。