基于改进变分模态分解和小波阈值法的单相接地故障电流降噪
2023-11-06王孔贤邵英王黎明
王孔贤, 邵英, 王黎明
(海军工程大学电气工程学院, 武汉 430033)
根据电力系统运行的经验表明,单相接地故障是电力系统输配电线路最频发的故障,现有的许多单相接地故障选线方法都是基于零序电流信号来实现的,这是由于单相接地故障发生后,故障线路与正常线路的零序电流信号的幅值和相位在暂态和稳态都存在很大的差异。吴春阳等[1]运用动态时间弯曲(dynamic time warping,DTW)规划原理,获得线路零序电流波形间的动态模式匹配距离矩阵,最后利用模糊C 均值聚类算法,实现单相接地选线。文献[2]利用Hausdorff 距离算法比较线路间的零序电流信号主要高频分量的波形差异进行故障选线。由此可见零序电流信号在故障选线过程中的重要性,但是在实际环境中由于电气设备间的电磁环境复杂,现场环境干扰严重等情况会导致故障录波装置采集到的故障零序电流信号噪声干扰严重,进而影响后续的故障选线,因此对含噪声零序电流信号进行降噪对提高后续故障选线准确率尤为重要。
现有的应用于零序电流信号降噪的算法主要都是采用经验模态分解[3]及其改进算法,缺乏扎实的理论基础,且鲁棒性较差。Dragomiretskiy等[4]在2014年提出了变分模态分解(variational mode decomposition,VMD)这一全新的非递归、自适应的信号处理方法,该方法克服了传统分解算法的不足,具有扎实的理论基础和更好的鲁棒性,可以抑制或避免模态混叠现象,适用于处理故障零序电流信号这种非线性、非平稳信号,但其在使用过程中需要对分解层数K和惩罚因子α这两个参数进行预先设置,否则会导致模态的过分解和欠分解,中心频率法[5-6]、瞬时频率均值法[7-8]、频谱峰值点法[9]都可以用来确定VMD参数,但是这些方法在K选取上并未考虑K和α间可能存在的相互影响,存在较大主观臆测性,且选取速度慢。而采用智能算法对VMD进行参数寻优[10-11]可以在一定程度上克服由于人的主观经验导致的误差。现提出采用北方苍鹰优化算法[12](northern goshawk optimization,NGO)对VMD算法进行改进优化。
在对故障零序电流信号进行降噪时,分解算法得到的模态成分比较复杂,需要重新筛选和处理后才能进行重构,现有的筛选方法主要采用给定相关系数阈值[3,13]或者利用各分量熵值大小排序[14]进行选取,前者的适用性较差,在某些噪声含量很大,各分量相关性很小的时候造成大量有用信号被直接剔除的问题,后者在完成熵值排序后,一般人为主观地筛选前几个分量进行重构,缺乏可靠性。现引入自适应相关阈值对分解后的分量进行筛选,对相关性小的噪声分量通过小波阈值降噪进一步提取其中的有用部分,最大限度地在含噪声零序电流信号中提取出有用信号。
现提出一种改进VMD和小波阈值法的单相接地故障零序电流信号联合降噪方法,首先,通过NGO优化算法对VMD分解的两个参数K与α进行优化选取,提高分解效果,对分解得到的IMF分量利用自适应相关阈值进行筛选,将IMF分量与原信号相关系数大于阈值的分量作为有效分量直接保留,将IMF分量与原信号相关系数小于阈值的模态分量进一步利用小波阈值法进行降噪,最后进行重构,通过搭建模型进行实验,并与小波阈值降噪方法、经验模态分解(ensemble empirical mode decomposition,EEMD)-小波阈值降噪方法、完全自适应噪声集合经验模态分解(complete ensemble empirical mode decomposition with adaptive noise,CEEMDAN)-小波阈值降噪方法以及定参数VMD小波阈值降噪方法进行对比,说明改进VMD和小波阈值法联合降噪方法的有效性,并且在标准测试信号Heavy Sine信号和Bumps信号中进行实验验证算法适用性。
1 基本理论
1.1 VMD原理
VMD的原理是将非平稳信号f分解为K个模态分量子信号uk,且每个分量有一个确定的有限带宽和中心频率ωk。变分问题就可以表示为寻求K个模态函数uk(t),使得每个模态的估计带宽之和最小,约束条件为各模态分量之和为输入信号f,构造过程中,首先对各个模态函数分量uk(t)进行Hilbert变换,获得其解析信号,其次将各个模态函数分量的解析信号与e-jωkt进行混合,将每个模态分量的频谱调制到相应的预估基频带,计算平移后信号梯度的L2范数平方来估计带宽[15]。整个变分问题的构造过程最终得到的表达式为
(1)
式(1)中:{uk}={u1,u2,…,uK}、{ωk}={ω1,ω2,…,ωK}分别为所有模态及其中心频率;∂t为对t求偏导数;δ(t)为狄拉克分布;*表示卷积。为了求解式(1),引入二次惩罚因子α和拉格朗日乘法算子λ将式(1)转换为非约束变分问题,其中α可以在高斯噪声存在的情况下保证信号的重构精度,拉格朗日算子使得约束条件保持严格性,增广拉格朗日函数表达式为
L({uk},{ωk},λ)=

(2)
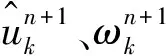
(3)
(4)
(5)
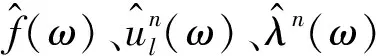
VMD算法的具体计算过程如下。
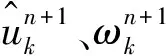
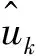
(6)
式(6)中:ε1为预设定的收敛误差。
1.2 NGO原理
北方苍鹰优化算法[12]通过模拟北方苍鹰在猎物狩猎过程中的行为对参数进行优化,下面对算法原理进行介绍,主要分为两个阶段,分别是识别猎物及攻击猎物阶段和追逐及逃生阶段,每个阶段的数学模型如下。
(1)识别猎物及攻击猎物阶段。这个阶段北苍鹰随机选择一个猎物,然后迅速攻击它,由于搜索空间中猎物的随机选择,该阶段增加了算法的搜索能力。该阶段是全局搜索,目的是识别最优区域,这一阶段的数学模型公式如式(7)~式(9)所示。
(7)
(8)
(9)

(2)追逐及逃生阶段。在北苍鹰攻击猎物后,猎物试图逃跑。因此,在一个追尾过程中,北方苍鹰继续追逐猎物,由于北苍鹰的高速飞行,它们几乎可以在任何情况下追逐猎物并最终狩猎,对这种行为的模拟提高了算法对搜索空间局部搜索的能力,该阶段是局部搜索,目的是找到最优解,这一阶段的数学模型公式如式(10)~式(12)所示。
(10)
(11)
(12)
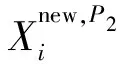
在根据上述NGO算法数学模型更新所有种群参数后,完成算法的迭代,此时确定了所有种群参数值、目标函数以及当前最优解,然后算法进入下一次迭代,种群成员根据式(7)~式(12)继续更新,直到完成最后一次迭代,整个迭代过程中获得的最优解作为给定优化问题的解。
1.3 IMF筛选
VMD分解后,各模态函数分量IMF 所包含的频带是不同的,噪声主导的分量中存在较多异常信号会导致与原信号之间的相关性降低,二者之间的相关系数会变小,而有用信号成分主导的分量与原信号相关性较好,二者之间的相关系数会较大,因此原信号与各分量信号之间的相关系数大小能够作为有效分量选取的依据,两种成分主导的分量之间存在一个相关系数的临界阈值[16-17],如果相关系数高于该阈值,则认为该分量中包含的是有用信号成分,如果互相关系数低于该阈值,则认为该分量中包含的是噪声或者异常成分,阈值rthr的计算公式如下。
(13)
(14)

1.4 小波阈值法
小波阈值法降噪的本质是对信号的滤波,将含噪声信号小波分解后得到原始信号和噪声的分解系数,且原始信号的分解系数大于噪声的分解系数,此时需要选取合理的阈值,通过阈值处理筛选出噪声并过滤掉噪声,将分解系数大于阈值的认为是由原始信号而来,保留相应的分量,将分解系数小于阈值的认为是由噪声信号而来,舍弃相应的分量,最后重构信号[18]。小波阈值法的关键是确定小波基函数、分解尺度、阈值函数和阈值的计算方法4个关键参数。对于小波基函数,工程上通常选择使用具有高阶消失矩的小波系,如dbn、symn、coifn小波系,对于阈值函数一般分为硬阈值和软阈值。硬阈值函数就是使高于阈值的小波系数不变而将低于阈值的小波系数变为0,硬阈值可以相对更好地保留信号的局部特征[19],但这种处理方式会使得在小波域在阈值处产生突变,造成信号重构后,可能会产生新的振荡,软阈值处理是将小波系数绝对值大于给定阈值的系数减去阈值,小于阈值的系数等于零。软阈值函数处理的信号会更加平滑,消除了硬阈值函数处理引起的局部突变[20],但软阈值函数存在恒定偏差的问题,重构后的信号幅度产生一定的失真[21],如图1所示为软硬阈值函数对比曲线图,处理前小波系数ω经过特定处理后得到ω′,T为阈值,可以看出硬阈值是不连续的,软阈值是连续的。
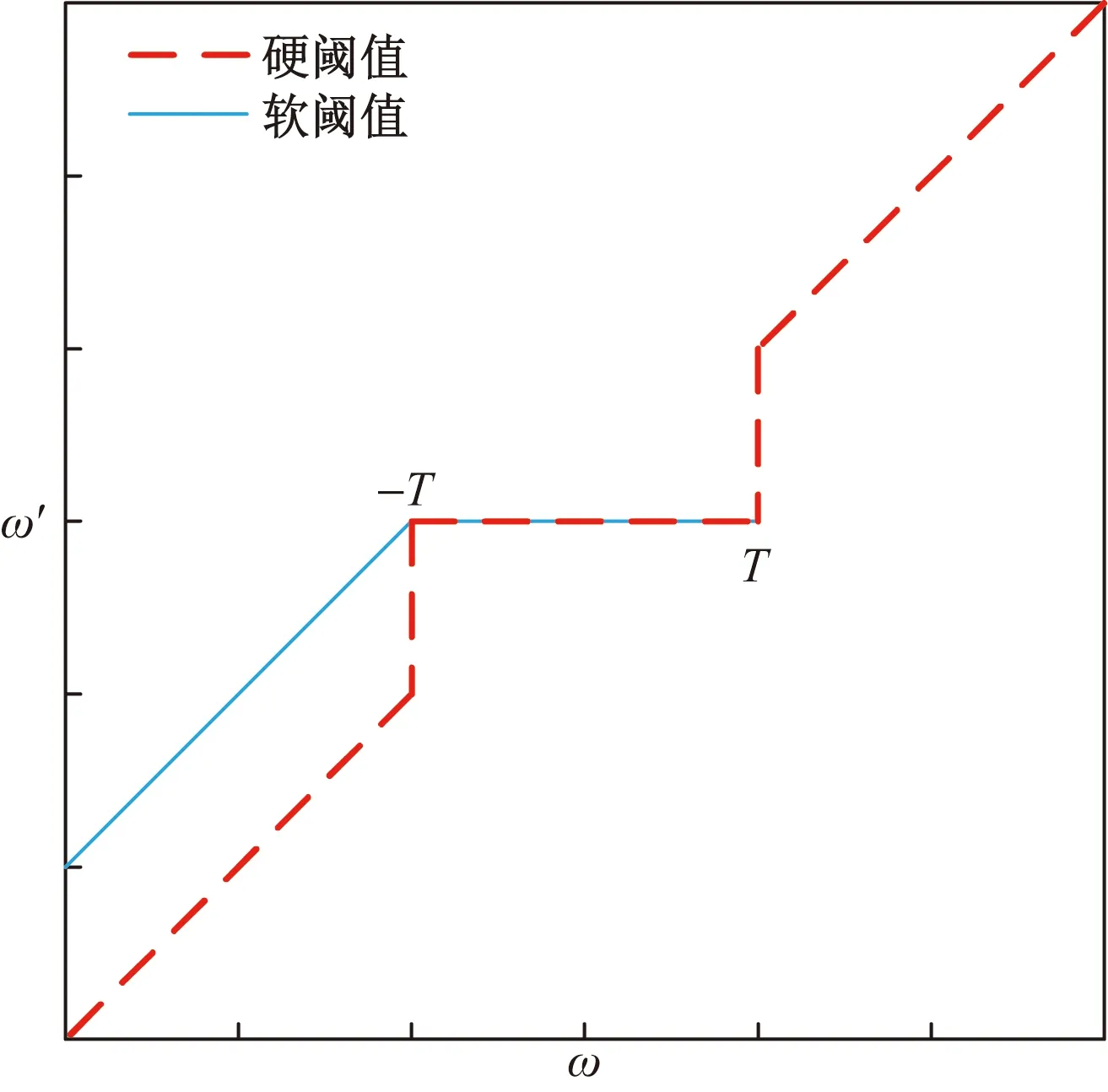
图1 软硬阈值函数对比曲线图Fig.1 Comparison curve of soft and hard threshold functions
对于阈值的计算方法,目前主流的计算方法有Sqtwolog 阈值、Minmax阈值、Rigsure阈值和Heursure 阈值。
2 降噪方法
2.1 NGO优化VMD
利用NGO优化VMD 参数提高VMD的性能,进行优化时,还需要设定一个目标函数,包络熵[22]可以反映分量的稀疏程度,零序电流信号经过VMD分解后,如果得到的IMF分量所含的噪声越多,则信号的稀疏程度越小,包络熵值就越大; 如果IMF分量的规律性很强,噪声越少,则信号的稀疏程度越大,包络熵也就越小。VMD分解后有K个分量就会有K个包络熵值,选择K个包络熵值中最小的作为局部最小包络熵值minEe,即为目标函数,整个优化过程就是要找到全局最小包络熵以及对应的最佳分量组合K和α。包络熵Ee的计算公式为
(15)
式(15)中:a(j)为信号VMD分解后的IMF分量经过Hilbert变换得到;bj为a(j)的归一化形式。NGO优化VMD算法的具体步骤如下,流程图如图2所示。

图2 NGO优化VMD流程图Fig.2 NGO optimization VMD flow chart
(1)NGO参数的初始化。K的取值范围为[2,10],α的取值范围为[500,20 000],种群的规模大小为30,最大迭代次数为15。
(2)对零序电流进行VMD分解,选择目标函数为最小包络熵值minEe,通过每次代入不同组合的K和α对minEe进行计算,再相互比较更新当前最佳目标函数值。
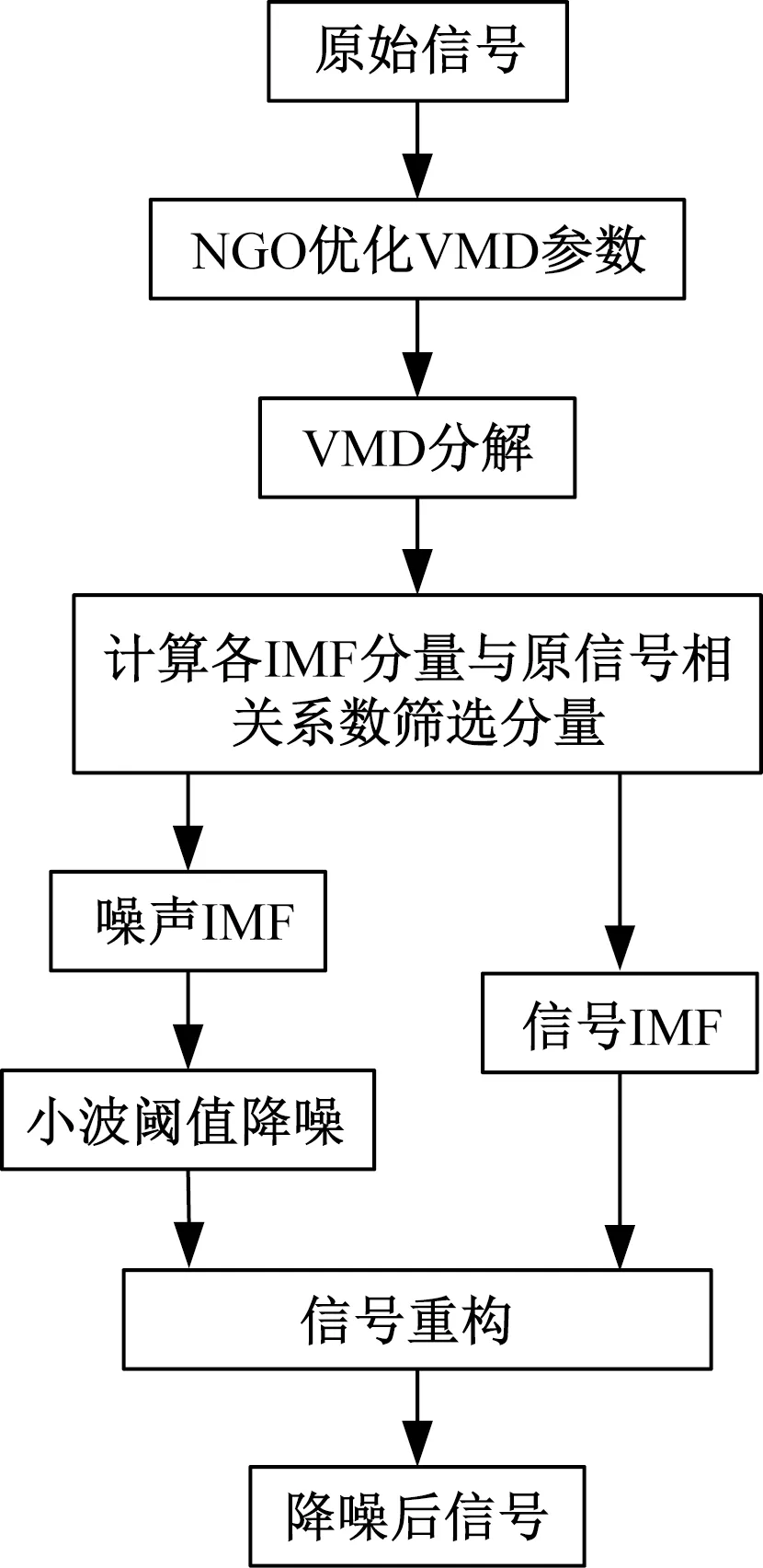
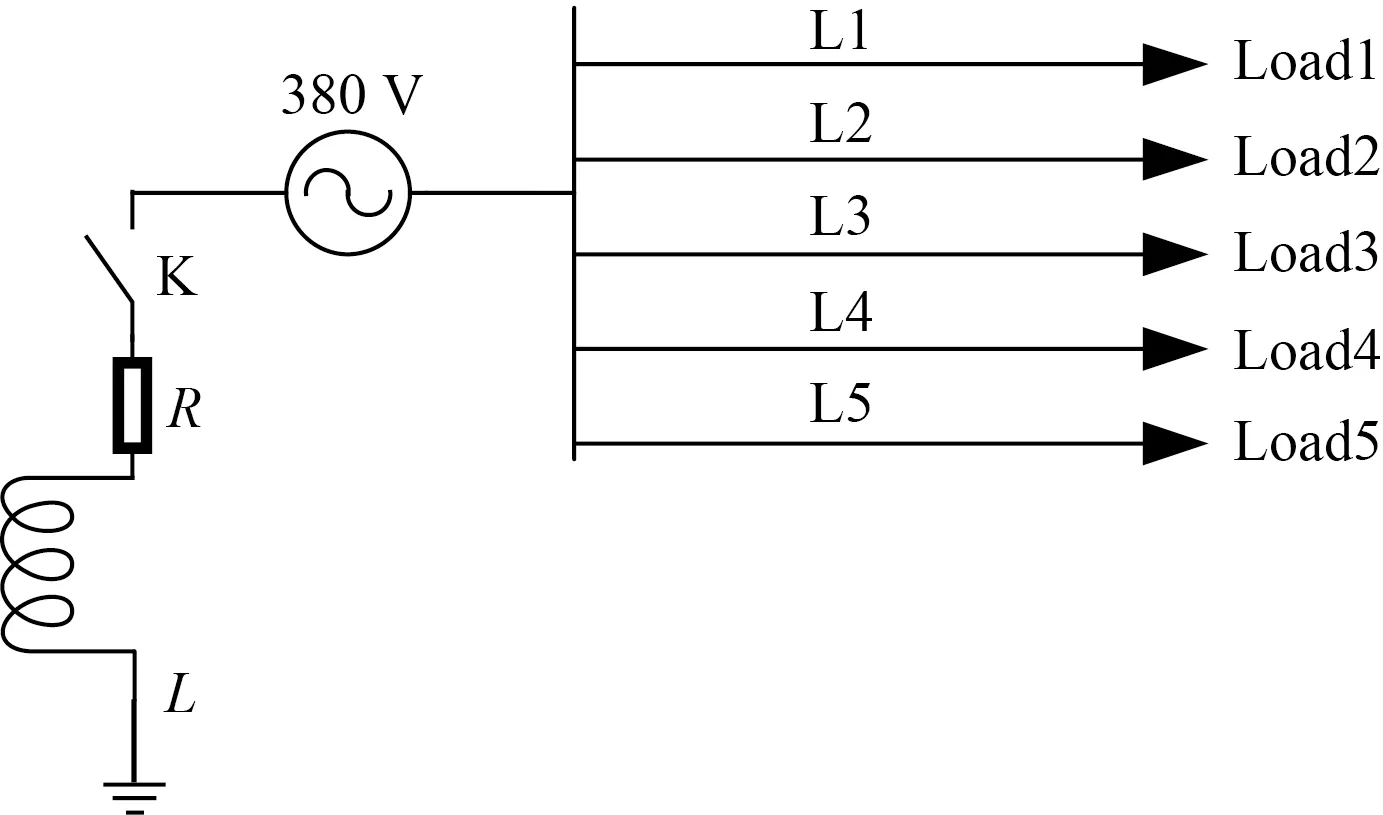
(3)确定是否终止迭代。如果t 其他参数对分解效果影响较小,设置为经验值,即噪声容忍度tau=0,初始化中心频率init=1,直流分量DC=0,收敛准则容忍度ε=1×10-7。 提出了一种新的基于 NGO-VMD和小波阈值法联合降噪的单相接地故障的零序电流降噪方法,具体流程如图3所示,主要步骤如下。 图3 NGO-VMD和小波阈值联合降噪流程图Fig.3 Flow chart of joint denoising by NGO-VMD and wavelet threshold (1)MATLAB中利用SimPowerSystems工具箱搭建了380 V的低压小电流接地的配电网模型,设置线路单相接地故障的不同故障条件,采集故障线路零序电流。 (2)利用小波模极大值对采集的零序电流进行初步的截断预处理,减小后续计算量,然后利用NGO算法对VMD 算法的参数进行优化,确定分解模态数K以及惩罚因子α。 (3)利用改进的VMD 方法对截断后的故障线路和非故障线路零序电流进行分解,得到一系列IMF分量,然后利用相关系数法筛选有效分量和噪声分量,对噪声分量进行小波阈值降噪,再将降噪后分量和有效分量进行重构。 利用MATLAB/Simulink的SimPowerSystems工具箱搭建了380 V的低压小电流接地的配电网模型,该模型共有 L1、L2、L3、L4、L5 五条出线,模型如图4所示,开关K断开采用中性点不接地系统。 R为接地电阻;L为接地电感;Load1~Load5分别为5条出线的等效负载 模型中主要模块及参数设置如表1所示,设定故障开始时刻为0.02 s,结束时刻为0.1 s,整个过程持续0.1 s,采集5个工频周期的数据,采样频率为40 kHz。 表1 主要模块及参数设置Table 1 Main modules and parameter settings 通过改变仿真模型中的故障过渡电阻、故障位置、故障类型以及故障初相角来模拟不同故障条件采集故障零序电流为后续进行算法分析打下基础,设计如表2所示故障样本集合。 表2 故障样本集合Table 2 Fault sample set 随机选择参数,当图4中配电网为中性点不接地系统时,设线路 L1的A相发生接地故障,故障点到线路首端距离LF为1.2 km,过渡电阻RF为 2 Ω, 故障初相角为90°,仿真得到的故障线路L1的零序电流波形图和非故障线路的零序电流波形图如图5所示。 图5 故障线路与非故障线路零序电流波形图Fig.5 Waveform diagram of zero-sequence current of fault line and non-fault line 从图5中可以看出,故障线路L1的零序电流波形无论是在相位上还是在幅值上都与非故障线路存在很大差别,零序电流是区别故障线路与非故障线路的重要信号,保证零序电流信号不被噪声污染,才能保证后续利用零序电流进行线路故障分析的准确性。 为了降低后续的计算量,对信号进行预处理,利用小波模极大值法检测出信号奇异的位置,即为零序电流突变位置,然后在此基础上,向前截取0.5个工频周期,向后截取1.5个工频周期的信号作为预处理后的暂态零序电流信号用于后续分析,截去多余部分,仅保留包含丰富故障信息的暂态部分。如图6所示为在上述故障情况下对故障线路L1进行小波模极大值截断预处理前、后的零序电流图,预处理前零序电流在0.04 s处发生突变,整个过程一共记录了0.1 s,突变过程很短暂,之后就进入稳态,后面属于重复的波形数据,而预处理后仅保留突变前0.01 s以及突变后0.03 s的波形,对暂态过程做了很好的记录。 图6 预处理前后故障线路的零序电流图Fig.6 Zero-sequence current diagram of fault line before and after pretreatment 建立小电流接地配网暂态等值电路,如图7所示,从电路原理上探讨零序电流的组成,由于LP远远大于L0,同时消弧线圈中的RP远小于等效回路中的R0。因此等效回路中可忽略消弧线圈的LP和RP对暂态电容电流的影响[23]。 U0为等效零序电源电压;R0为等效电阻;L0为等效电感;C为系统等值零序电容的总和;RP和LP分别为消弧线圈的有功损耗电阻和电感 根据图7,由基尔霍夫电压定律可列方程如下。 (16) 式(16)中:iC和iL分别为暂态电容电流和电感电流;Um为相电压的幅值;φ为发生故障时相电压初相角;即故障合闸角;ω为电路振荡频率。对方程求解可得到暂态电容电流iC和暂态电感电流iL表达式为 (17) iF=iC+iL =(ICM-ILM)cos(ωt+φ)+ (18) 式(18)中:第一项(ICM-ILM)cos(ωt+φ)为稳态分量,其余为暂态分量,从式(18)中不难看出,故障零序电流的特征不仅与配电网的参数有关,也与故障合闸角φ有关[24]。φ=0°时,即故障发生在相电压过零点处,此时故障零序电流为 (19) 此时,故障零序电流的主要成分为工频交流分量、高频振荡分量和衰减直流分量组成,衰减直流分量占主要成分,高频振荡分量占比很小。φ=90°时,即故障发生在相电压峰值时,此时故障零序电流为 iF=(ICM-ILM)cos(ωt+90°)+ (20) 此时,故障零序电流的主要成分为工频交流分量、高频振荡分量组成,高幅值的高频振荡分量占主要成分,衰减直流分量为0。故障发生的时刻不同,故障线路和正常线路的零序电流含量是不同的,低频段具有不同含量的衰减直流分量,高频段具有不同的幅值和相位特性。 利用所搭建的配电网模型生成单相接地故障零序电流仿真信号验证所提联合降噪算法的性能和有效性,再利用MATLAB自带的标准测试信号Heavy Sine和Bumps信号进一步验证降噪算法的适用性。 利用NGO优化算法改进VMD 算法搜索最优参数组合,以故障条件下采集到的零序电流信号为例,VMD参数寻优过程的迭代曲线如图8所示,经过4次迭代搜索得到了全局的最优解,此时的包络熵值最小,为3.985 1,该全局最优解对应的参数K=7和α=2 162,将其代入VMD 算法中。 图8 NGO-VMD寻优迭代曲线Fig.8 NGO-VMD optimization iteration curve 图9为对故障零序电流信号进行优化分解后得到的3个模态分量对应的时域图和频谱图,纵坐标为各个IMF分量的幅值,从图中可以看出信号分解充分,没有出现模态混叠的现象,其中低频分量IMF1表征低频衰减直流分量,瞬时频率在50 Hz左右,高频分量IMF2、IMF3表征暂态高频电容分量,分解后的时频谱图基本符合前面分析得出的故障零序电流的频段分布。 图9 模态分量对应的时域图和频谱图Fig.9 Time domain diagram and frequency spectrum diagram corresponding to modal components 由于现场利用故障录波装置采集故障零序电流信号会受到白噪声的干扰,这会对后续的故障选线产生不利影响,因此本节为模拟现场真实的故障零序电流信号, 在仿真生成的原始信号上叠加高斯白噪声, 这里还是以上文故障条件下采集到的零序电流信号为例,在采集到的故障零序电流信号中加入10 dB的高斯白噪声,得到的加噪信号的波形如图10所示。 图10 加噪信号波形图Fig.10 Noise added signal waveform 对加噪信号进行NGO-VMD分解,优化得到的参数K=9、α=862 5,计算各个模态分量与加噪信号的相关性,如图11所示,利用式(1)求得的相关系数阈值为0.149 1,IMF1~IMF13的相关系数均大于阈值视为有效分量,直接保留,IMF4~IMF19进行小波阈值降噪。 图11 各分量与加噪信号的相关程度Fig.11 Correlation between each component and the noise added signal 对小波阈值法的4个关键参数进行讨论,首先对小波基函数进行确定。分解尺度取为6,阈值计算方法取为Sqtwolog 阈值,阈值函数采用软阈值,利用dbn(n=1,2,…,10)、symn(n=1,2,…,10)、coifn(n=1,2,…,5)这25个小波基函数对噪声分量进行降噪,然后与有效分量重构,计算处理后信号的SNR,从中选择出最优的小波基函数组合,试验结果如图12 所示,可以发现db3的降噪效果最好,将加噪信号信噪比(signal to noise ratio,SNR)提升至14.131 dB,选用db3作为小波基函数。 图12 小波基函数选择Fig.12 Selection of wavelet basis function 在小波基函数确定为db3后,在阈值函数采用软阈值的前提下,对阈值计算方法和分解尺度进行讨论,采用Sqtwolog 阈值、Minmax阈值、Rigsure阈值和Heursure 阈值4种阈值计算方法,分解尺度取1~15进行实验,结果如图13所示,分解尺度取到10以后,4种阈值计算方法的信噪比都基本不再变化,分解尺度为10时,信噪比达到最大,其中采用Sqtwolog 阈值(固定阈值)的信噪比最高,为14.155 1 dB,其他3种阈值计算方法信噪比最大值如表3所示。 表3 4种阈值计算方法得到的最大信噪比 图13 阈值计算方法和分解尺度选择Fig.13 Threshold calculation method and decomposition scale selection 4种阈值计算方式中,Sqtwolog 阈值的信噪比最高,这是由于Minmax阈值和Rigsure阈值比较保守,当噪声在信号的高频段分布较少时,这两种阈值估计方法效果较好,但是对于故障零序电流信号,噪声主要分布在高频段,而Sqtwolog 阈值降噪比较彻底,效果更显著,虽然可能会出现把有用的信号误认为噪声去掉的情况,但是在VMD分解筛选时,已经把大部分的有用信号得以保留,所以对剩余噪声分量采用Sqtwolog 阈值相比其他阈值计算方法效果会更好。 对于软阈值函数和硬阈值函数,软阈值避免硬阈值“一刀切”引起的突变,效果更好,采用硬阈值时信噪比为13.636 5,比软阈值得到的结果小。下文中所有的小波阈值去噪都将采用小波基函数为db3,分解尺度为8,阈值计算方法为Sqtwolog 阈值,阈值函数为软阈值函数的参数设置。 改进VMD算法和小波阈值联合去噪后的信号与仿真生成的原始信号的对比图如图14所示,可以看出,在故障发生后的暂态部分,降噪效果明显,两个波形基本一致,在故障发生前的部分,降噪后波形与原始信号波形略有差距,但不会对后续的故障选线造成影响。 图14 去噪后信号与加噪前信号对比图Fig.14 Comparison diagram of signal after denoising and signal before denoising 进一步对算法有效性进行分析,在仿真生成的故障零序电流信号中加入5、10、15、20 dB的高斯白噪声,并将改进VMD-小波阈值降噪方法与小波阈值降噪方法、EEMD-小波阈值降噪方法、CEEMDAN-小波阈值降噪方法以及定参数VMD小波阈值降噪方法进行对比,EEMD-小波阈值降噪方法中EEMD的高斯白噪声的标准差设置为0.2,添加噪声的次数为100次,CEEMDAN-小波阈值降噪方法中CEEMDAN的高斯白噪声的标准差设置为0.2,添加噪声的次数为100次,最大迭代次数为20次,定参数VMD小波阈值降噪方法中参数采用最普遍的设置,即K=10、α=2 000,用信噪比SNR和均方根误差(root mean squared error,RMSE)作为评价降噪效果的评价指标进行评价,实验结果如表4所示。 表4 不同降噪方法效果评价 从表4中可以看出,改进VMD-小波阈值降噪方法相较于EEMD-小波阈值降噪方法、CEEMDAN-小波阈值降噪方法等其他的模态分解算法有着显著的优势,而且相较于定参数VMD-小波阈值降噪方法,说明改进VMD-小波阈值降噪方法采用优化分解参数对提高联合降噪方法信噪比的有效性,信噪比越小时,即噪声含量越高时,优势越明显,信噪比提高了35.99%,均方根误差降低了30.88%(输入信噪比为5 dB),噪声含量较小时,信噪比也提高了5.52%,均方根误差降低了12.78%(输入信噪比为20 dB)。 Heavy Sine信号和Bumps信号是MATLAB提供的标准测试信号之一,也是典型的非线性、非平稳信号,选用这两个标准测试信号来进一步验证联合降噪算法的适用性。通过MATLAB生成长度为1 024的模拟Heavy Sine信号和Bumps信号,并加入相应振幅大小的高斯白噪声,最后得到信噪比为5、10、15、20 dB的仿真信号用于实验分析,结果如表5和表6所示,分别为Heavy Sine信号和Bumps信号的实验结果,图15和图16分别是Heavy Sine信号和Bumps信号加噪后与降噪后的对比图。 表5 不同降噪方法对Heavy Sine信号降噪效果评价Table 5 Effect evaluation of different denoising methods on Heavy Sine signal 图15 Heavy Sine信号降噪效果对比图Fig.15 Comparison diagram of Heavy Sine signal denoising effect 图16 Bumps信号降噪效果对比图Fig.16 Comparison diagram of Bumps signal denoising effect 从表5和表6可以看出,采用改进VMD-小波阈值降噪方法在对Heavy Sine信号和Bumps信号进行降噪处理时,无论是SNR还是RMSE,都比其他算法结果更好,说明对噪声分量的剔除是有效的,而且从图15和图16也可以直观地看出降噪后信号与加噪信号的差异,其中的噪声分量被有效剔除。 针对输配电线路发生单相接地故障时,现场环境干扰较为严重导致故障录波装置采集到的故障零序电流信号含有大量噪声,导致故障识别准确率低的问题,提出了一种改进VMD和小波阈值联合降噪方法,并搭建模型进行实验,与其他降噪方法进行对比,研究结论如下。 (1)采用北方苍鹰智能群优化算法对变分模态分解算法中分解层数K和惩罚因子α两个参数进行优化选取,克服了传统的基于人工经验选取的不足,提高了变分模态分解的效果与效率。 (2)利用相关系数法对优化分解后的故障零序电流信号进行筛选,对相关性低于阈值的噪声分量进行小波阈值降噪,通过实验确定小波阈值去噪采用小波基函数为db3,分解尺度为8,阈值计算方法为Sqtwolog 阈值,阈值函数为软阈值函数的参数设置。 (3)通过在仿真生成的故障零序电流信号中加入5、10、15、20 dB的高斯白噪声,与小波阈值降噪方法、EEMD-小波阈值降噪方法、CEEMDAN-小波阈值降噪方法以及定参数VMD小波阈值降噪方法进行对比实验,改进VMD和小波阈值联合降噪方相较于定参数VMD-小波阈值降噪方法,信噪比提高了5.52%~35.99%,均方根误差降低了12.78%~30.88%,且相比其他降噪算法也具有明显优势。 (4)通过在MATLAB的标准测试信号Heavy Sine信号和Bumps信号加入5、10、15、20 dB的高斯白噪声,与其他算法对比实验,结果表明改进VMD和小波阈值联合降噪方法降噪效果更好,说明所提降噪方法具有适用性。2.2 降噪流程
3 信号特性分析
3.1 模型搭建




3.2 零序电流信号特性分析



4 实验分析
4.1 零序电流信号分解
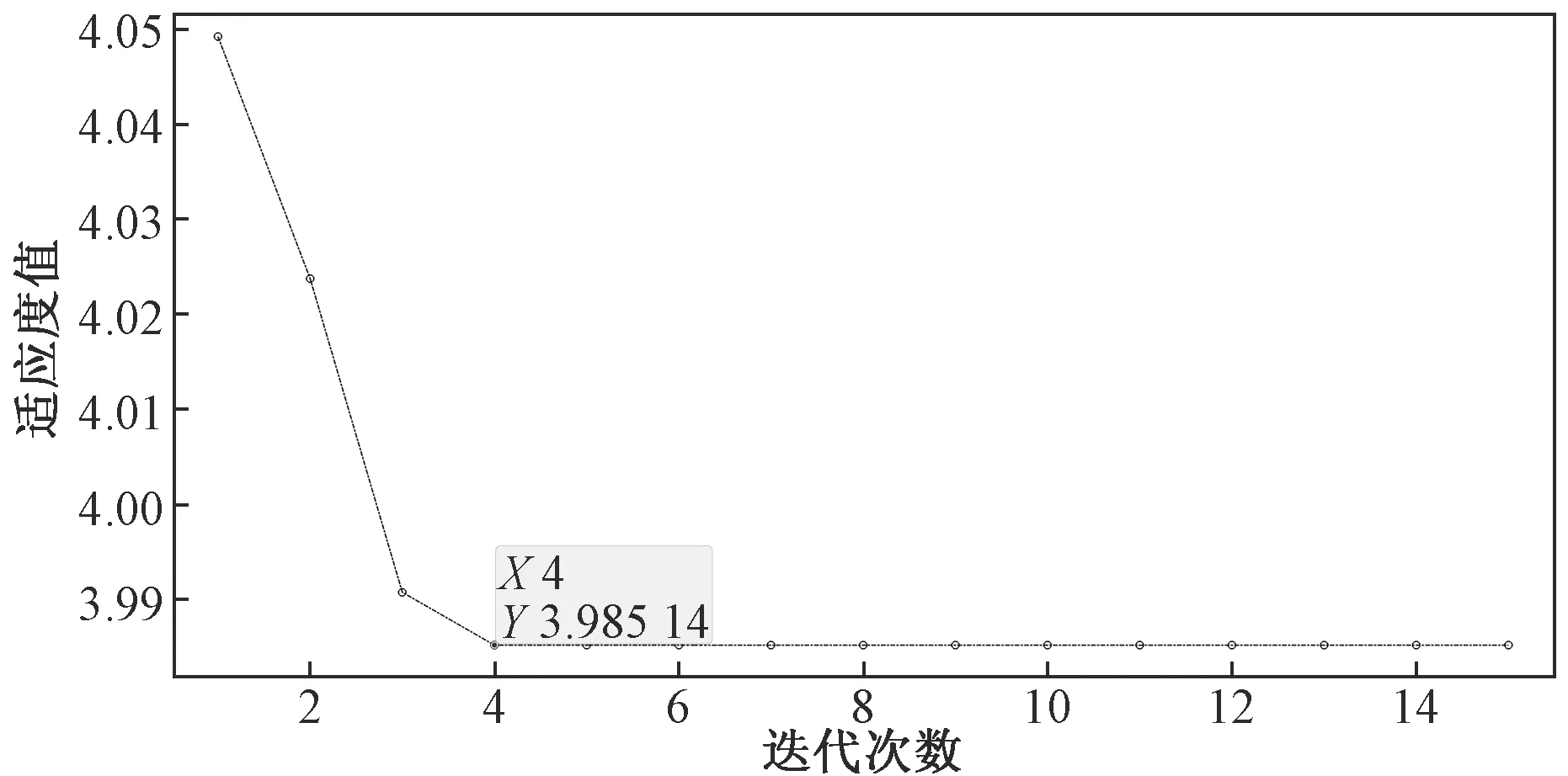
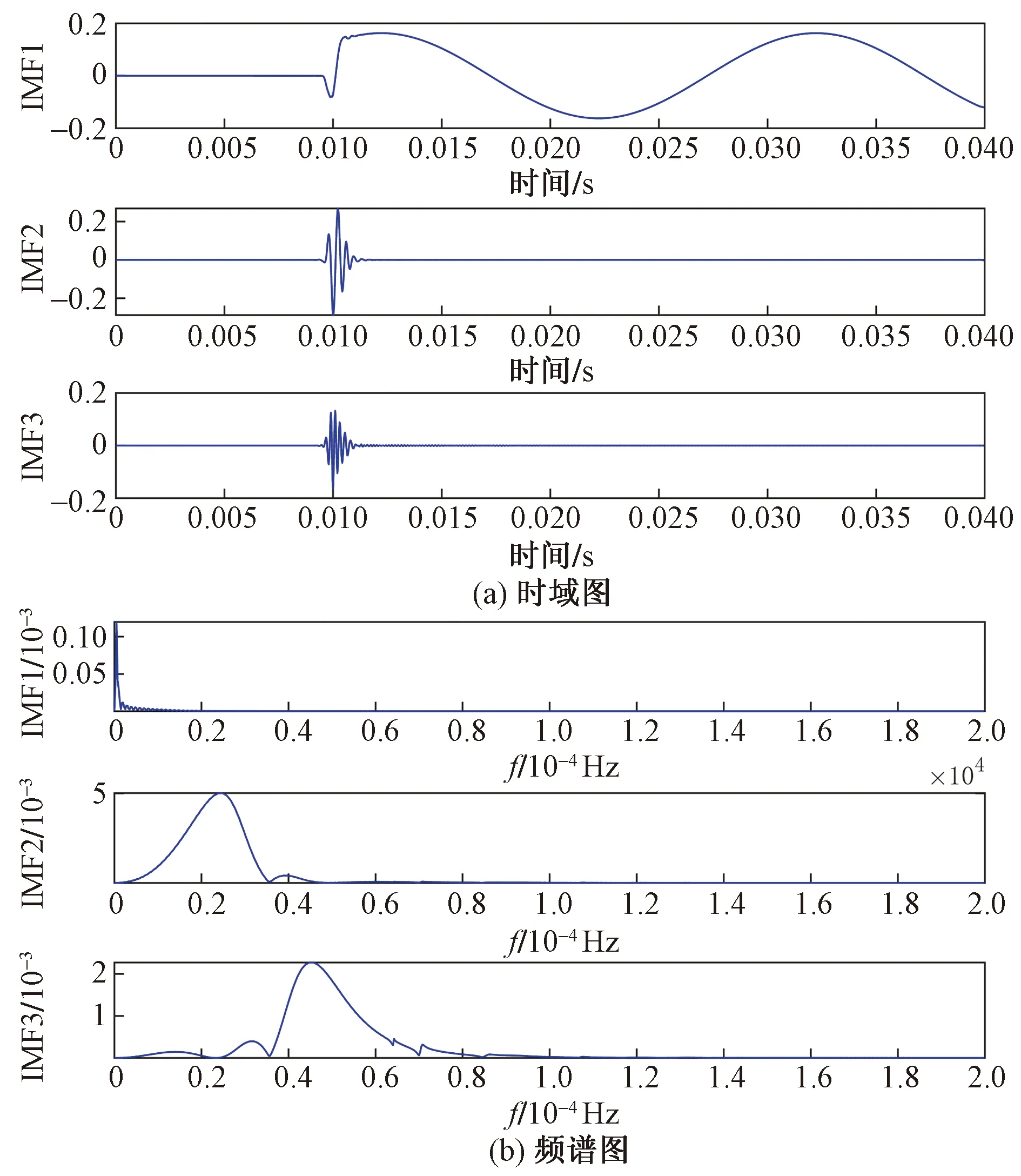
4.2 联合降噪
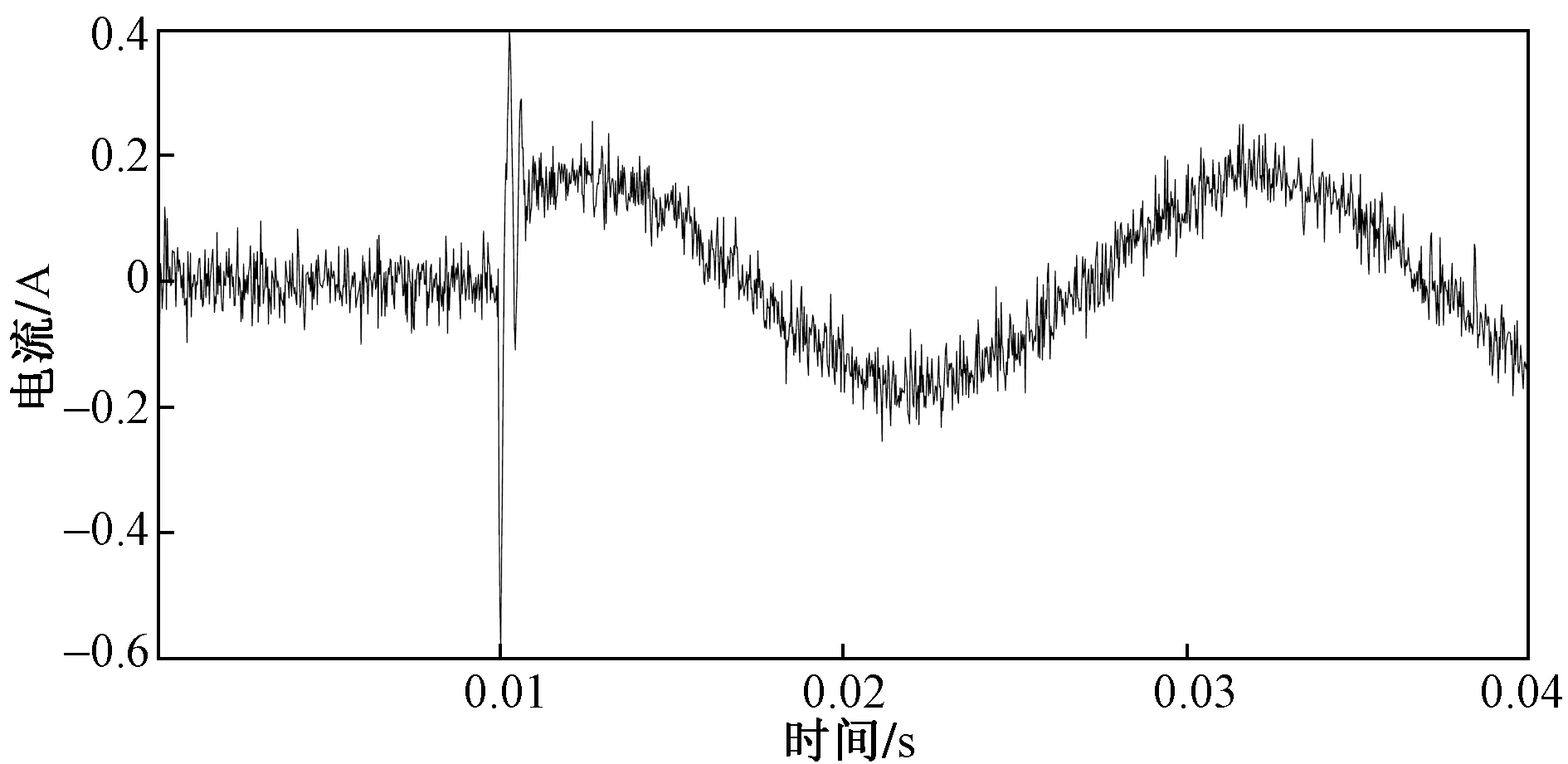

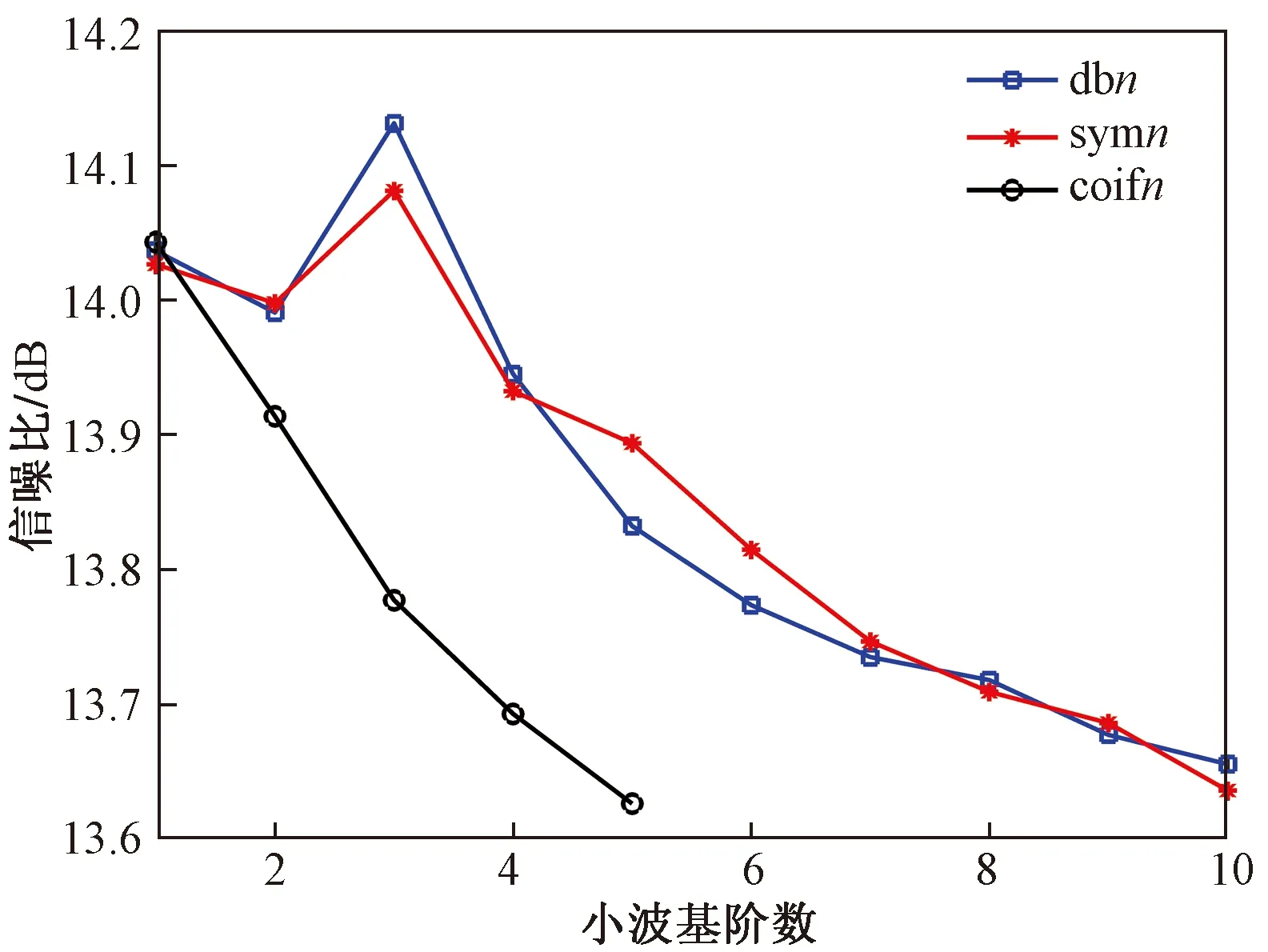


4.3 对比试验

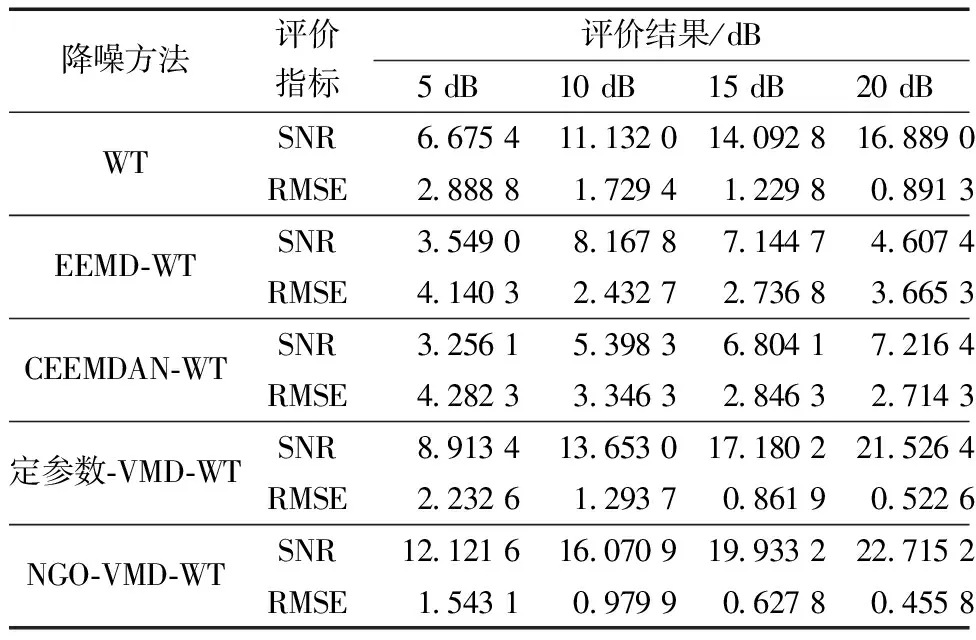
4.4 标准测试信号分析

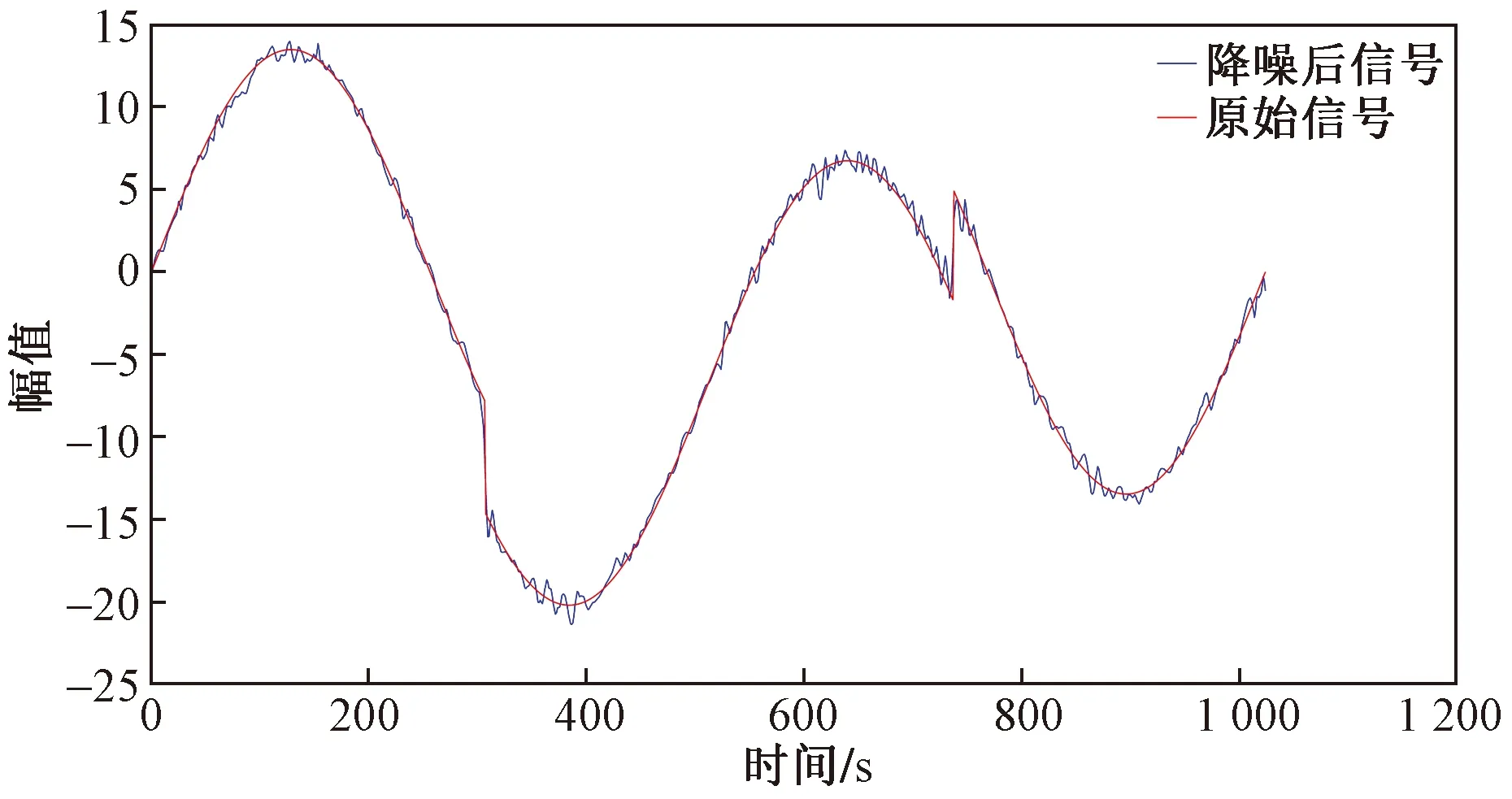
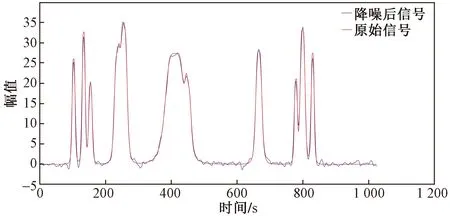
5 结论
