行星际激波导致内磁层脉冲电场的模拟研究
2023-11-04张典钧刘文龙杜俊峰张钊
张典钧, 刘文龙*, 杜俊峰, 张钊
1 北京航空航天大学空间与环境学院, 北京 102206 2 北京航空航天大学空间环境监测与信息处理工信部重点实验室, 北京 102206
0 引言
行星际激波(Interplanetary shocks,IPS)是影响内磁层物理过程的重要因素,一般伴随着日冕物质抛射(CME)或共转相互作用区(CIR)产生(Gibson et al., 2009),可能会导致剧烈的地磁活动甚至是磁暴和亚暴(Cao et al., 2008, 2010; Fu et al., 2011, 2012; Liu et al., 2009, 2013, 2016; Ma et al., 2020; Shi et al., 2013, 2014; Sun et al., 2015; Wang et al., 2010; Yu et al., 2015, 2017; Zhang et al., 2020, 2022; Zong et al., 2007, 2017).行星际激波导致内磁层压缩的这段时间也被称为磁暴急始期(Chapman and Bartels, 1940),在这一期间,由于行星际激波压缩导致的地球磁场急速抬升,内磁层会感应产生出全球尺度的西向的脉冲电场(Kim et al., 2009; Korotova et al., 2018; Schmidt and Pedersen, 1988; Shinbori et al., 2004; Sun et al., 2015; Tian et al., 2016; Zhang et al., 2018).由于脉冲电场方向平行或反平行于内磁层的粒子漂移方向,脉冲电场会导致高能粒子的加速,同时也会在电漂移的作用下快速地发生注入(Blum et al., 2021; Hudson et al., 2017; Kanekal et al., 2016; Patel et al., 2019; Schiller et al., 2016; Xiao et al., 2020).
Blake等(1992)初次报道了1991年3月24日行星际激波事件,CRRES卫星在夜侧内磁层观测到了持续时间大约2 min且幅度约40 mV·m-1的双极性(Bi-polar)脉冲电场,同时观测到相对论电子的注入,其深度达到了L=2.5 的位置,脉冲电场的双极性特征是由磁层依次被太阳风压缩和舒张产生的向内和向外的等离子体流动导致的.Li等(1993)通过对1991年3月24日事件观测的电磁场进行建模,并结合实验粒子成功模拟出观测中的相对论电子的漂移回声信号(drift-echo).Kress等(2007)利用磁流体力学方法(MHD)模拟的2003 年万圣节磁暴急始期中观测到的脉冲电场也成功再现出漂移回声信号,脉冲电场幅度为10 mV·m-1且持续时间为1~2 min.Foster等(2015)报道了范艾伦卫星观测的2013年10月8日的行星际激波事件,发现环向的脉冲电场可以使初始动能为3~4 MeV的电子在短时间内获得0.4 MeV的加速.这一系列观测研究表明,行星际激波导致的脉冲电场与相对论电子的快速输运和加速过程之间有着非常紧密的联系,因此研究行星际激波的脉冲电场对理解内磁层动力学问题有重要意义.
Zhang等(2018)利用2013—2017年行星际激波事件期间的范艾伦卫星电场观测数据研究了脉冲电场的特性,尤其是行星际激波到达地球之后直接由压缩产生的第一个脉冲电场的时间演化以及振幅大小的特性.与Schmidt和Pedersen(1988)利用GEO-2卫星以及Shinbori等(2004)利用Akebono卫星的观测结果相同,统计结果中的脉冲电场符合沿环向向西的特征,然而不同的是脉冲电场日侧的幅度普遍大于夜侧的幅度,同时脉冲电场在日侧的持续时间也普遍小于夜侧.并且通过将电场数据与太阳风观测数据比较,在日侧,初始脉冲电场的振幅与太阳风动压变化幅度呈正相关,而在夜侧很难产生强烈的脉冲电场,除非是像2015年3月17日的极端的行星际激波事件,充分揭示了产生的脉冲电场的第一个周期的幅度和演化可能是由太阳风直接控制的.另一方面我们也基于脉冲电场空间分布的统计结果,讨论了行星际激波期间发生的内磁层电子的注入和加速行为,对于空间分布宽度为10个磁地方时且幅度为3.36 mV·m-1的脉冲电场,可以使L=4的高度漂移的4.3 MeV的相对论电子在77 s内获得289 keV的加速.
在本文我们将利用美国密歇根大学开发的空间天气模组(Space Weather Modeling Framework;SWMF)对2015年12月19日行星际激波对地球磁层的作用进行模拟,研究脉冲电场的分布以及演化特征,并与Zhang等(2018)的统计观测结果进行对比.本文第1节将对观测数据以及模型进行介绍,第2节将介绍卫星观测数据以及数值模拟的主要结果.
1 数据与方法
1.1 观测数据
本研究的观测部分使用了以下卫星和地磁台站的观测数据:首先是位于日地拉格朗日L1点的Wind卫星数据,主要使用仪器有磁强计MFI仪器(Magnetic Field Investigator, Lepping等(1995))以及三维等离子体分析仪3DP仪器(3d-Plasma Analyzer, Lin等(1995)).Wind卫星于L1点测量的太阳风数据会被均匀地插值到时间精度为5 s的时间轴上,并作为模拟的输入条件使用.其次是位于内磁层的范艾伦卫星,主要使用仪器为磁强计EMFISIS仪器(Electric and Magnetic Field Instrument Suite and Integrated Science, Kletzing et al., 2013)以及电场探针EFW仪器(Electric Field and Wave, Wygant et al., 2013).其中EFW仪器只提供了电场的mGSE(modified GSE)坐标下的Y和Z分量的测量数据,X分量需要根据磁冻结的假设并结合EMFISIS仪器测量的磁场数据计算得到.最后是OMNI数据中的对称地磁水平分量SYM-H指数(Iyemori, 1990),用来确定行星际激波到达地球磁层的确切时间.
1.2 模型介绍
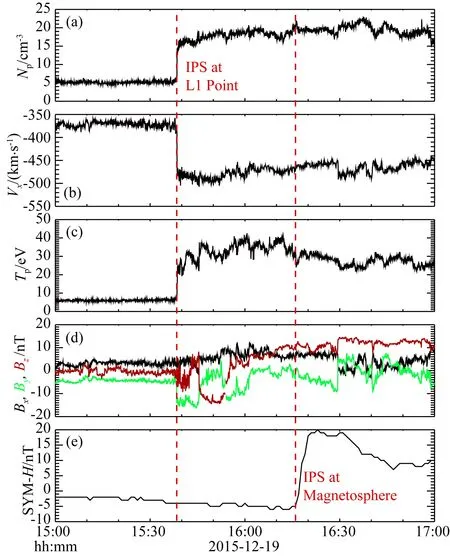
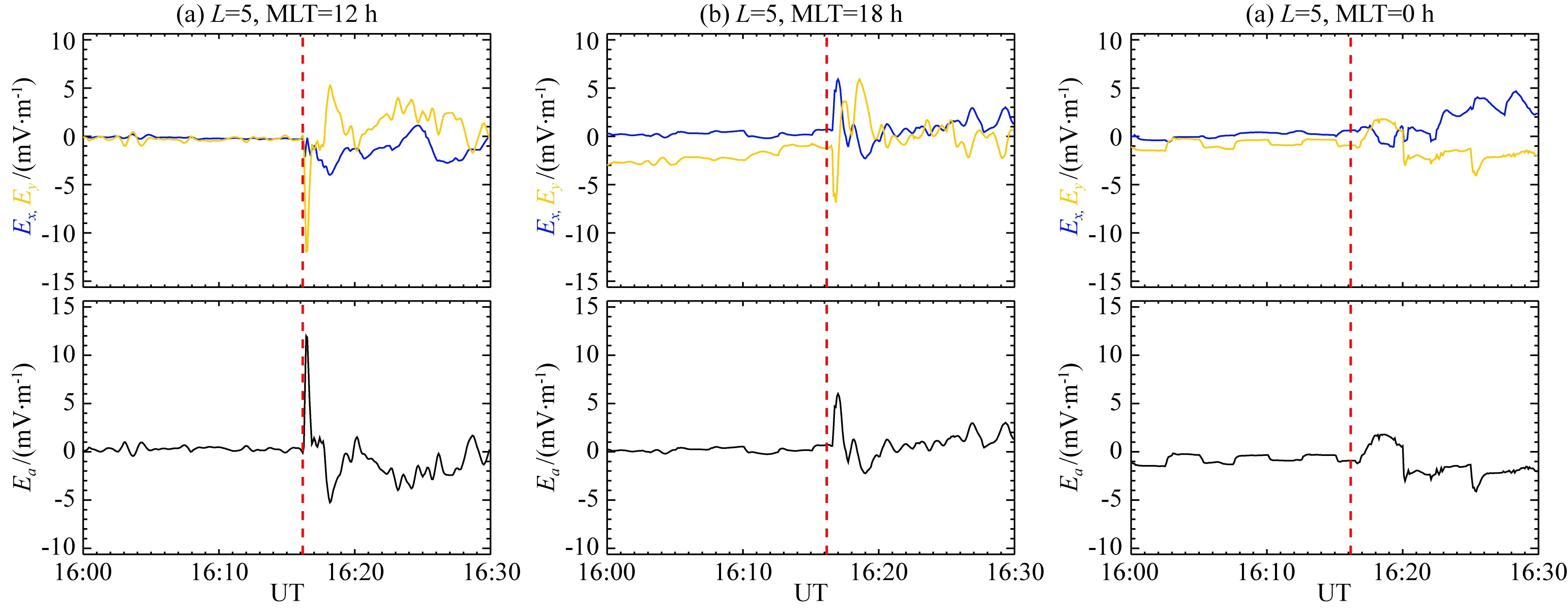
本研究的数值模拟部分所使用的是美国密歇根大学开发的SWMF(Space Weather Modeling Framework)模组(Tóth et al., 2005),用来研究行星际激波导致的脉冲电场在内磁层各个位置的时间演化特性.这个模型框架集成了全球磁流体力学BATS-RUS(Block-Adaptive Tree Solar Wind Roe-Type Upwind Scheme)模型(Powell et al., 1999)、环电流RCM(Rice Convection Model)模型(Toffoletto et al., 2003)以及电离层模型(Ridley et al., 2004).本数值计算模型主要用于对太阳风磁层相互作用过程的可视化,在之前的研究工作中有很好的表现(Gong et al., 2022; Wei et al., 2019; Yu and Ridley, 2008, 2009, 2011).全球MHD模型主要以Wind卫星的观测数据作为太阳风输入条件来求解理想磁流体力学方程组.模型设计为网格求解,对于r<4RE的位置网格的计算精度为1/8RE,而对于4 在图1中,我们展示了2015年12月19日Wind卫星在L1点于大约15∶45 UT观测到的快前向行星际激波(图中用IPS指代行星际激波):质子数密度Np从5 cm-3增大到了15 cm-3(见图1a),太阳风速度Vx大小从375 km·s-1增大到490 km·s-1(见图1b),对应的太阳风动压Pd从2 nPa增大到了7 nPa,并且质子温度Tp从6 eV增长到了25 eV(见图1c),同时伴随着行星际磁场的各个分量的变化(见图1d).如节1.2所述,图1a—d所展示的行星际激波的观测结果同时被用作SWMF模拟的输入条件.OMNI数据记录到SYM-H指数在16∶17 UT左右出现从-5到20 nT的增长,表示在这个时刻于L1点观测的行星际激波到达并压缩了地球磁层,导致了全球尺度的磁场增强(见图1e). 图1 Wind卫星在L1点测量的(a)质子密度、(b)太阳风速度GSE坐标下的X分量、(c)质子温度和(d)GSE坐标下磁场矢量观测数据以及(e)OMNI数据库的SYM-H指数.两个红色垂直虚线分别代表行星际激波依次到达日地L1点以及地球磁层的时间Fig.1 (a) Proton number density,(b) X component of solar wind velocity in GSE coordinate, (c) proton temperature and (f) magnetic field vector in GSE coordinate obtained from Wind spacecraft measurement at L1 point and (e) SYM-H index obtained from OMNI database. Two vertical dashed lines respectively represent the interplanetary shock′s arrival at the Sun-Earth L1 point and the Earth′s magnetosphere 图2展示了范艾伦B卫星于2015年12月19日16∶17 UT左右的轨道示意图.卫星大致运行于磁地方时为10点且L值大致为5.8的内磁层日侧区域,所观测到的电磁场对行星际激波的响应展示在图3a—e中.范艾伦B卫星的EFW仪器测量到脉冲电场幅度为7 mV·m-1,方向指向晨侧并且略微指向磁尾,即沿环向向西,上升沿时间大约为60 s(见图3a—b);同时EMFISIS仪器观测到磁场主要为Z方向上从120 nT到160 nT的抬升(见图3e).这些是典型的内磁层电磁场对行星际激波的响应特征,与之前的观测和模拟结果相符合(Cattell et al., 2017; Kanekal et al., 2016; Korotova et al., 2018). 图2 范艾伦B卫星的轨道信息示意图,其中箭头代表卫星运行方向Fig.2 A schematic of the orbit information of Van Allen Probe-B, where arrows represent the direction of spacecraft motion 图3 范艾伦B卫星的电磁场观测结果(左)和SWMF电磁场模拟结果(右).GSE坐标下电场的X和Y分量的数据(a—b和f—g)以及磁场的X、Y和Z分量数据(c—e和h—j).红色垂直虚线代表行星际激波导致的脉冲电场的起始时间Fig.3 Van Allen Probe-B observational results (left) and SWMF numerical result (right). (a—b and f—g) electric field X and Y components and (c—e and h—j) magnetic field X, Y and Z components in GSE coordinate. The red vertical dashed lines indicate the onset time of IPS-induced impulsive electric field 范艾伦B卫星位置的SWMF对行星际激波的电磁场响应的模拟结果展示在图3f—j中.图3f和g所展示的模拟结果中脉冲电场的幅度约为12 mV·m-1,大于观测结果的7 mV·m-1,但是从脉冲电场的X和Y的分量比值可以看出,观测结果中沿环向向西的方向特征被很好地再现了出来,并且随时间演化的趋势也是基本一致的.相比之下,图3h—j所展示的模拟结果的磁场变化与观测结果在幅度、方向以及时间演化的特征都基本相同.总的来说,观测与模拟结果之间具有很好的一致性,因此SWMF的结果很好的地模拟出了内磁层对行星际激波的响应过程. 从图3所示的观测和模拟结果中可以初步发现脉冲电场沿环向向西的特征,在这里我们需要利用SWMF模拟结果来进一步验证脉冲电场的分布特征.图4展示的是赤道面上L值从4到7的区域内行星际激波达到之后电场的第一次响应的幅度和方向的信息.可以看到,脉冲电场在大部分的区域内都符合沿环向向西的特征,同时日侧的脉冲电场幅度(12 mV·m-1)也普遍大于夜侧(4 mV·m-1).这两个特征都与Zhang等(2018)对脉冲电场的观测统计结果相一致. 图4 SWMF模拟结果中,行星际激波到达之后第一个脉冲电场的幅度和大小在赤道面的分布图.箭头长度和颜色代表脉冲电场幅度,右上图例展示了5 mV·m-1大小的脉冲电场对应的箭头长度,右侧的色标也可以作为幅度的参考,虚线圆作为L=2、4、6以及地球同步轨道的位置参考Fig.4 The amplitude and orientation of initial impulsive electric field after IPS′s arrivalst the Earth′s magnetosphere in the SWMF simulation result. Both length of arrows and color represent the amplitude of the impulsive electric field. The legend and color bar can both be a reference for the amplitude. The dashed circles are the references for the location of L=2, 4 and 6 and the geosynchronous orbit 图5中展示的是从图4所示的SWMF模拟结果中L=5的高度上磁地方时分别为12、18和24(即正午、昏侧、午夜)的位置提取出的电场随时间的演化情况.同样也可以看出图4结果所示的脉冲电场的幅度和方向的分布信息.除此之外也容易看到,随着磁地方时从正午转向午夜,脉冲电场的幅度逐渐变小的同时,环向电场Ea的上升沿时间Δt(从电场为0到第一次达到峰值的时间)也在逐渐变大. 图5 SWMF模拟结果中L=5的高度上磁地方时分别为(a)12、(b)18和(c)24的位置的脉冲电场演化,从上至下分别为GSE坐标下X(蓝色)和Y(橙色)方向的电场以及环向(黑色)电场Fig.5 The impulsive electric field evolution in SWMF simulation result at the positions where MLT equals (a) 12, (b) 18 and (c) 0, respectively. From top to bottom, the electric fields in the X (blue) and Y (orange) directions and the azimuthal (black) electric field in GSE coordinates, respectively 图6展示了SWMF模拟结果中脉冲电场的上升沿时间大小Δt在不同的L上随磁地方时的分布图.可以看出,Δt的大小对磁地方时有明显的依赖性:日侧的Δt基本保持在30~45 s的范围,而随着位置越靠近午夜Δt变得越来越大,甚至在磁地方时为3的位置Δt可以达到150 s以上;而相比之下Δt对L值的依赖性并不明显,尽管在正午侧高L值的Δt倾向大于低L值的Δt.因此Δt的大小主要依赖于磁地方时,此结果与Zhang等人(2018)的统计结果中的日夜不对称的特征相一致.在Zhang等人(2020)的工作中验证了Δt的大小是由当地的快磁声波速度决定,当地的快磁声波速度越快,快波锋面的传播就越快,Δt就越小,日侧夜侧磁层的背景磁场的差异决定了两个区域的平均快磁声波速度不同,同样存在日夜不对称性,因此Δt基本可以确定是与脉冲的传播相关. 图6 SWMF模拟结果中脉冲电场的上升沿时间大小Δt在不同的L上随磁地方时的分布图,L的大小用颜色区分Fig.6 Distribution of the rising time Δt of simulated impulsive electric field with MLT at different L. L value is distinguished by colors 从以上对模拟结果的分析可以看出,磁层对行星际激波的响应是一个全球尺度的过程,其产生的脉冲电场在不同地方时和L值区域都可被观测到.Zhang等(2018)利用范艾伦卫星的观测结果,对多个行星际激波事件期间的脉冲电场进行了统计分析,得到其激发和分布的观测特征,但受限于单点卫星观测的影响,无法确定脉冲电场在一个事件中的传播规律和幅度变化.本文所开展的模拟研究提供了一个全球尺度的完整的脉冲电场对行星际激波的响应图像,从模拟结果中可以清晰地分辨其传播时间和幅度变化特征. 我们利用SWMF模拟了2015年12月19日的行星际激波事件,并结合范艾伦B卫星的电场观测,验证了Zhang等(2018)对行星际激波导致的脉冲电场的统计结果,得到了如下结论: (1)2015年12月19日的范艾伦B卫星的电场观测与SWMF模拟的相同位置的电场演化结果一致; (2)脉冲电场主要沿着环向向西的方向,并且日侧的脉冲电场幅度大于夜侧的幅度,而日侧的脉冲电场上升沿时间小于夜侧的上升沿时间; (3)我们利用SWMF模拟很好地验证了Zhang等(2018)利用范艾伦卫星对脉冲电场的统计研究结果. 致谢本工作由国家自然科学基金(41821003和41974194)提供支持.感谢NASA CDAWeb(http:∥cdaweb.gsfc. nasa.gov/)提供了Wind卫星、范艾伦卫星数据,以及OMNI提供了SYM-H指数数据.感谢密歇根大学空间环境模拟中心(CSEM)开发的SWMF和BATS-R-US工具.感谢中国广州的天河二号国家超级计算机提供的计算.2 观测和模拟结果
2.1 行星际激波的观测
2.2 内磁层响应的观测和模拟


2.3 脉冲电场的分布特性


3 结论
