浅水区海浪电磁噪声对大地电磁阻抗估计的影响
2023-11-04潘林冬李予国葛佳琦吴云具
潘林冬, 李予国,*, 葛佳琦, 吴云具
1 中国海洋大学海洋地球科学学院, 山东青岛 266100 2 海底科学与探测技术教育部重点实验室, 山东青岛 266100
0 引言
海洋大地电磁测深法(MT)是利用天然场源在海底介质中产生的感应电磁场,通过海底电磁采集站(OBEM)观测这些感应电磁场,研究海底深部地质构造和矿产资源分布的一种地球物理方法.在频带0.05~0.8 Hz范围内,海浪运动因切割地磁场可以在距水面数十米的深度处产生数百皮特斯拉(pT)的感应磁场(Crews and Futterman,1962;Fraser,1965,1966;Weaver,1965;Lezaeta et al.,2005;Duan et al.,2020),约为地球变化磁场的数十倍(Fraser,1966;Lezaeta et al.,2005;张自力等, 2006; 张宝强, 2018; 周春, 2019;Duan et al.,2020).因此,通常认为浅水区地球变化磁场受海浪感应磁场的影响较大,从而使得海洋MT阻抗估计不佳(Lezaeta et al.,2005;Duan et al.,2020).然而,大地电磁阻抗是由水平电场和水平磁场的比值确定的,只考虑海浪感应磁场对地球变化磁场的影响是不够全面和深入的.需要同时考虑海浪感应电场和磁场对海洋MT场的影响.
海浪运动感应电磁场(简称海浪感应电磁场)的研究始于20世纪60年代.在感应磁场随时间变化项很小可以忽略不计(即∂B/∂t=0)的情况下,利用毕奥萨法尔定律计算了海浪感应磁场,并分析了海浪感应磁场在空气中(Crews and Futterman,1962)和海水中(Warburton and Caminiti,1964)的传播特征.Maclure等(1964)利用微分方程计算了海浪感应磁场.Weaver(1965)在计算无限水深海浪感应磁场时分析了感应磁场随时间变化项的影响,并且认为可以将∂B/∂t近似为零.前人通过观测的海洋磁场数据验证了海浪感应磁场理论(Fraser,1965,1966;Klein et al.,1975;Podney,1975; Podney and Sager,1978; Ames and Vehslage,1981; 张海滨, 2008; 张自力等, 2008; 吕金库, 2012; 熊雄等, 2015;费春娇等, 2018).在浅水情形下,海底电场垂直分量中海浪感应电场能量突出,而水平电场分量则由较大的大地电场控制(Håland et al.,2012;Wu et al., 2023).可见,海浪感应电场和海浪感应磁场对大地电场和地球变化磁场的影响不同.Shimizu和Utada(2015)推导了海水运动感应电磁场阻抗和倾子的表达式,并探讨了利用海啸运动感应电磁场阻抗和倾子探测海底介质电导率分布的可能性.但是该研究主要着重于深水区且频率范围3.3×10-5Hz到0.02 Hz内的情形,而没有探讨浅水情形下海浪电磁噪声对海洋MT阻抗估计的影响.
本文在Weaver(1965)和Larsen(1971)海水运动感应电磁场理论研究的基础上,基于三层海洋地电模型推导了有限水深情形下海浪感应电磁场表达式,并详细地分析了海浪运动频带内浅海区MT阻抗估计结果不佳的原因.结构安排如下:首先,根据海浪感应电磁场模型响应分析其传播特征;然后,借鉴MT场趋肤深度和阻抗(Cagniard,1953)的定义推导出海浪感应电磁场趋肤深度和阻抗的表达式,对比分析了海浪感应电磁场与MT场趋肤深度和阻抗的差异;最后,引入“复合阻抗”的概念,并结合实测数据特点分析海浪感应电磁场对MT阻抗估计的影响.
1 海浪感应电磁场和MT场的“复合阻抗”
在海浪运动频带内,海底电磁采集站采集和记录的数据中同时包含海浪感应电磁场信号和MT场信号.因此,利用在海底采集和记录的电磁数据得到的阻抗是这两种类型感应电磁场的综合响应.本文将由两种或两种以上场源产生的感应电磁场计算得到的阻抗称为“复合阻抗”.
1.1 海浪感应电磁场的趋肤深度和阻抗
三层海洋地电模型如图1所示.我们建立笛卡尔直角坐标系,假定x轴指向北为正,y轴指向东为正,z轴指向朝下为正.令海平面处z=0 m;空气层电导率为零;海水电导率为σ1(S·m-1),海水层厚度为d(m);海底层介质(基岩)电导率为σ2(S·m-1);电磁信号接收仪(OBEM)置于海底.
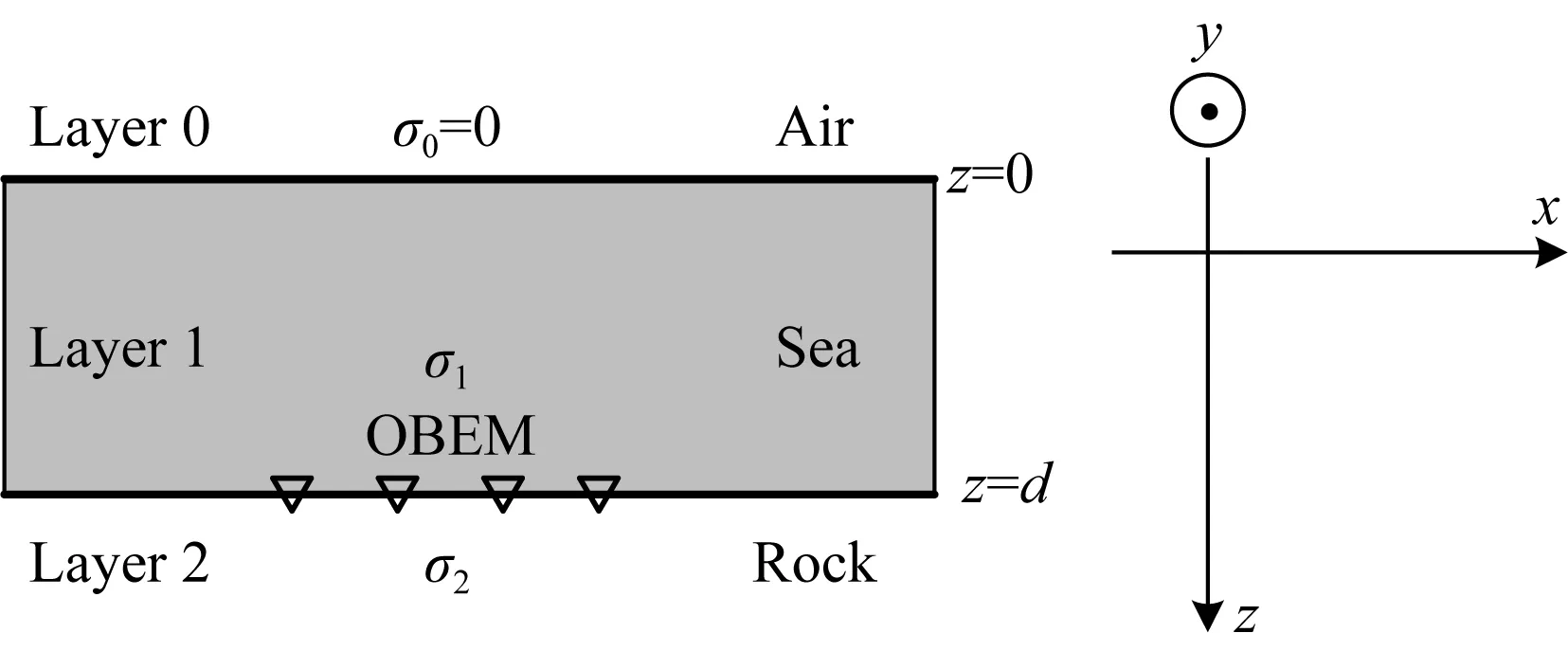
图1 三层海洋地电模型Fig.1 Three-layer ocean geoelectric model
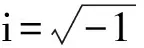
(1)
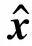
ω2=pgtanh(pd).
(2)
以速度V运动的海浪质点因切割地磁场F而产生感应电流,从而激发感应电磁场,其所满足的麦克斯韦方程为
(3)
其中,H表示磁场(A·m-1),J表示电流密度(A·m-2),E表示电场(V·m-1),σ表示电导率(S·m-1),μ=4π×10-7H·m-1表示真空磁导率.磁感应强度B与磁场H满足关系B=μH.假设地磁场F在空间中均匀分布,其表达式为
(4)
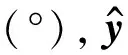
Larsen(1971)的研究表明,在海水层中海浪感应电磁场在其运动平面内的感应电流密度为0,即Jx=Jz=0.并且,与海浪运动平面垂直方向上的感应磁场为0,即Hy=0.
根据式(1),如令
(5)
则海浪速度可以写为V=v(z)e-i(ωt+px).对于均匀层状地电模型,海浪感应电场和磁场具有下列形式(Larsen,1971):
E=e(z)e-i(ωt+px),H=h(z)e-i(ωt+px).
(6)
由式(1)—(6)可以得到空气中(z<0)、海水层(0≤z≤d)和海底介质中(z>d)海浪感应电场分量(ey)和感应磁场分量(hx和hz)表达式(推导过程详见附录):
hz=Qepz,hx=-iQepz;z<0
-cosIcosθsinh[p(d-z)]}}
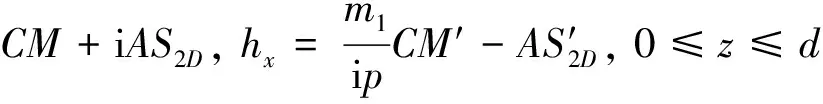
(7)
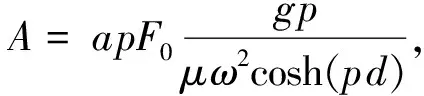
CM=C1em1z+C2e-m1z,CM′=C1em1z-C2e-m1z
S2D=icosIcosθsinh[p(d-z)]
+sinIcosh[p(d-z)],
S′2D=icosIcosθcosh[p(d-z)]
+sinIsinh[p(d-z)].
(8)
用式(7)可以计算得到海水和海底介质中的海浪感应电磁场.海浪感应电磁场相位部分e-i(ωt+px)的幅值为1保持不变,不影响海浪感应电磁场的幅值,因其具有周期性,不同时间t计算得到的海浪感应电磁场只在x方向上发生平移.图2为t=0 时刻海浪感应水平电场Ey(a)、水平磁场Bx(b)和垂直磁场Bz(c)在垂直断面(xz)内的分布.
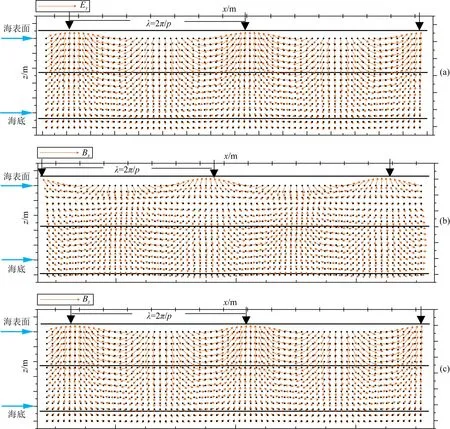
图2 海浪电场水平分量Ey(a)、磁场水平分量Bx(b)和垂直分量Bz(c)在海水和海底介质中的分布 黑线表示电磁场等相位点(黑色箭头所指位置)的连线.蓝色箭头所指位置分别对应海表面和海底.橙色箭头长度和指向分别 表示电磁场的相对大小和传播方向,尾部黑点表示海浪质点的平衡位置.λ表示海浪的波长.Fig.2 The distribution of horizontal electric component Ey (a), horizontal magnetic component Bx (b), and vertical magnetic component Bz (c) of OWEM fields in seawater and seabed The black line indicates the isophase line of EM fields at locations marked by the black arrow. The blue arrow corresponds to the sea surface and the sea bottom. The direction and length of the orange arrow indicate the propagation and the relative size of EM fields, respectively, and the tail black dot indicates the equilibrium position of the ocean waves particle. λ indicates the wavelength of ocean waves.
由图2可见,海浪感应电场和磁场等相位点连线(黑线)的形态为直线,且在同一深度处电磁场的幅值一致,这意味着海浪感应电磁场以平面波的形式在海水和海底介质中传播,该特征与MT场类似.
在海浪感应电磁场中,我们引入趋肤深度和阻抗(Cagniard,1953)的概念.趋肤深度是衡量电磁场能量衰减快慢的物理量,趋肤深度越大,代表电磁场能量衰减的越慢,反之,则越快.阻抗为电场水平分量与磁场水平分量的比值,它能够反映海底介质的电性结构.
海浪感应电磁场的复波数m2可以写为
(9)
m2的实部控制电磁场的衰减速度,虚部影响相位.故可得海浪电磁(OWEM)场在海底介质中的趋肤深度表达式为
由式(10)可知,海浪感应电磁场趋肤深度同时受到海底介质电导率、频率和水深的影响.
由海底介质中海浪感应电磁场表达式可以计算得到海底处阻抗表达式为
(11)
由式(11)可知,海浪电磁阻抗的相位不受海浪感应电磁场初相位的影响.
通常情况下,海浪运动方向受到风向的影响,具有三维性,其激发的感应电磁场也具有三维性.任意方向运动海浪的速度V可以经过矢量分解到正北向(x方向)和正东向(y方向).由二维海浪产生的感应电磁场可知,沿x方向传播的海浪,会激发相同方向的感应磁场Hx和与之垂直的感应电场Ey和感应磁场Hz.同理,沿y方向传播的海浪,会激发相同方向的感应磁场Hy和与之垂直的感应电场Ex和感应磁场Hz.
图3展示沿方向l运动的海浪产生的感应电场水平分量(El(z))和磁场水平分量(Hl(z)).其中,θ′表示海浪运动方向与x轴的夹角.与MT场类似,三维海浪感应电磁场水平分量可以分解成两组正交的场Ex,Hy和Ey,Hx.其中,Ex和Hy构成海浪感应电磁场的TE极化方式,即沿y方向运动的海浪激发出TE(横电)波型;Ey和Hx构成海浪感应电磁场的TM极化方式,即沿x方向运动的海浪激发出TM(横电)波型.它们的关系式为:
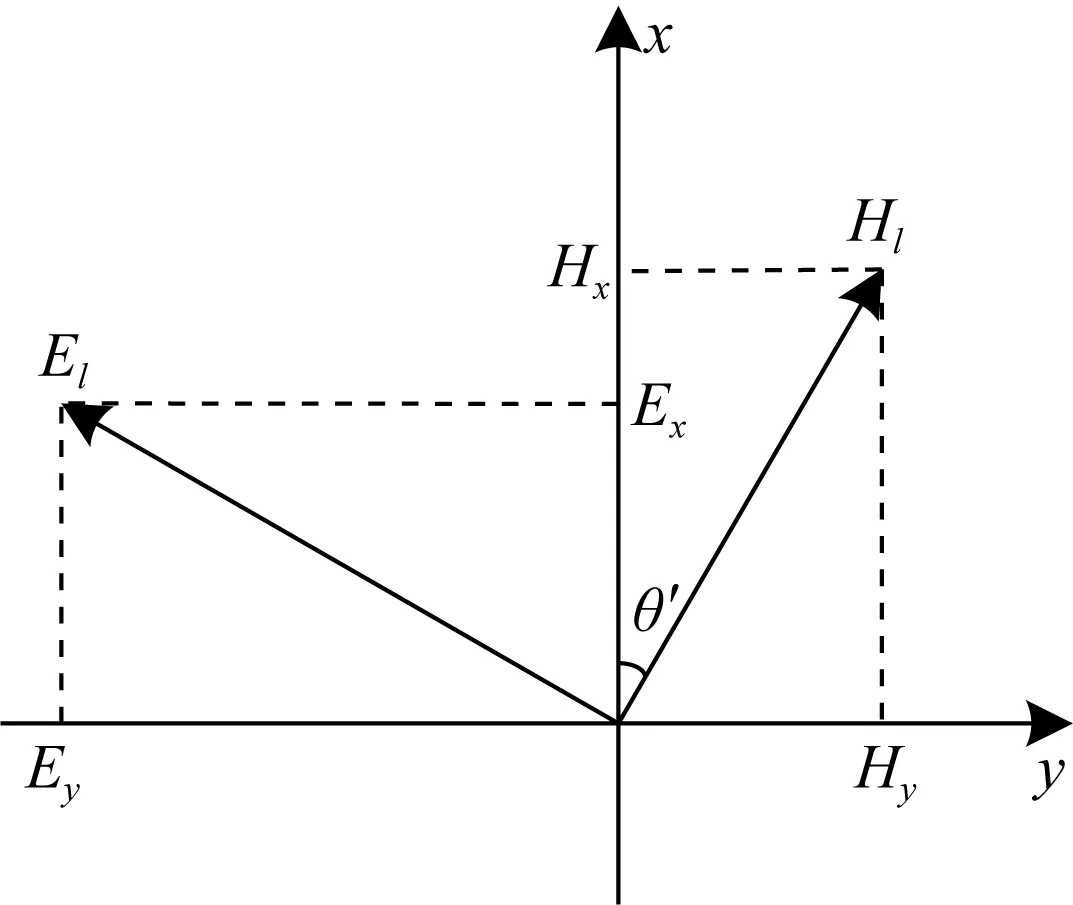
图3 电磁场正交分解Fig.3 Orthogonal decomposition of EM fields
TE极化方式:
(12)
TM极化方式:
(13)
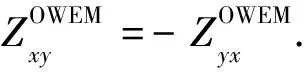
1.2 复合阻抗
利用未进行海浪电磁噪声压制的海底电磁数据直接进行阻抗估计,所得到的阻抗为“复合阻抗”,它会同时受到海浪感应电磁场和海洋MT场的影响,其表达式可以写为
(14)
其中,Z表示阻抗(Ω),EMT和HMT分别表示大地电场和地球变化磁场.由式(14)可知,当两种电磁场(海浪感应电磁场或大地电磁场)中某一种电磁场的强度较大时,则“复合阻抗”趋近于该种感应电磁场所对应的阻抗.
令Kwm=|HOWEM|/|HMT|,地球变化磁场初相位为φMT,海浪感应磁场的初相位为φOWEM,令φwm=φOWEM-φMT,称为初相位差.将式(11)代入式(14),可得“复合阻抗”表达式为
(15)
其中,|ZMT|和β分别表示MT场的阻抗幅值和相位,|ZOWEM|和α分别表示海浪感应电磁场的阻抗幅值和相位.海底处大地电磁场阻抗定义为(Cagniard,1953):
(16)
(17)
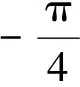
2 海浪感应电磁场和海洋MT场的趋肤深度和阻抗对比分析
2.1 趋肤深度
MT场的趋肤深度定义为(Cagniard,1953):
(18)
对比式(10)和式(18)可得,海洋MT场趋肤深度相较于海浪感应电磁场趋肤深度而言,它仅与海底介质电导率和频率有关.设置海底介质电导率的范围为10-5~5 S·m-1,频率范围0.05~0.8 Hz以及海水深度范围为10~400 m.将设置的参数代入式(10)和式(18)得到两种感应电磁场趋肤深度.图4为不同参数下海浪感应电磁场趋肤深度与MT场趋肤深度的对比.
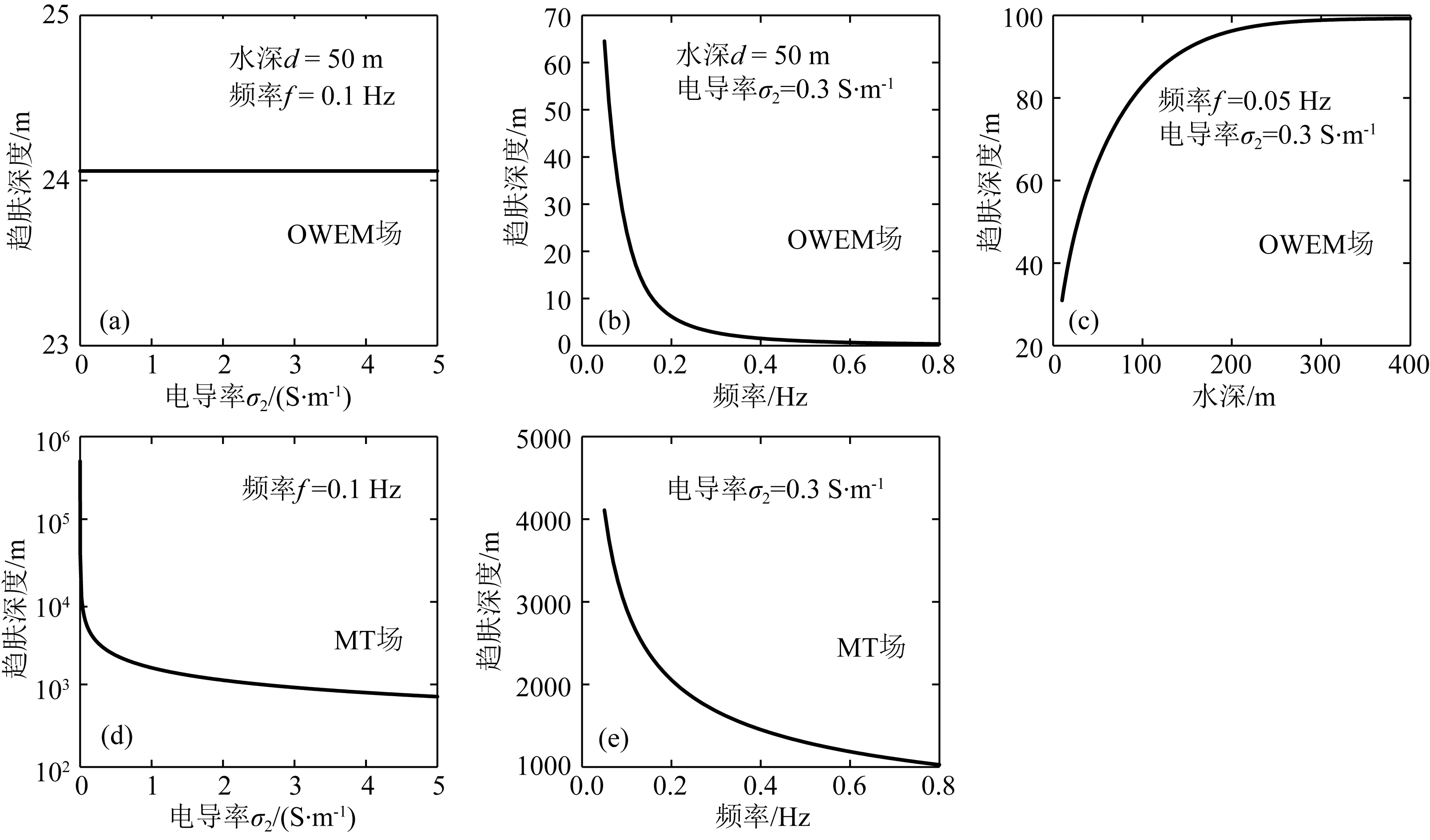
图4 海浪感应电磁场和MT场的趋肤深度对比 两种电磁场趋肤深度与海底介质电导率(海浪感应电磁场(a)和MT场(d))和频率(海浪感应电磁场(b)和MT场(e))的关系; (c)海浪感应电磁场趋肤深度与水深的关系.Fig.4 The skin depth comparison of OWEM fields and MT fields The relationship between the skin depth of two electromagnetic fields and the conductivity of the medium below the seafloor (OWEM fields (a) and MT fields (d)), the frequency (OWEM fields (b) and MT fields (e)); (c) The relationship between the skin depth and water depth of OWEM fields.
由图4a可知,当水深和频率一定时(如水深d=50 m,频率f=0.1 Hz),海浪感应电磁场趋肤深度基本不受海底介质电导率的影响.当海底介质电导率和水深一定时(如σ2=0.3 S·m-1,水深d=50 m),海浪感应电磁场趋肤深度随着频率的增大而减小(图4b).当海底介质电导率和频率一定时(如σ2=0.3 S·m-1,频率f=0.05 Hz),海浪感应电磁场趋肤深度随着水深增大而增大(图4c).因此,在水深小于400 m的情形下,海浪感应电磁场趋肤深度小于100 m.这意味着海浪感应电磁场在海底介质浅层能量就衰减到十分微弱,不能携带更多地球深部的电性信息.由图4d和图4e可知,MT场趋肤深度随着海底介质电导率(频率)的增大而减小.对比图4a和图4d(图4b和图4e)可得,在相同条件下,海浪感应电磁场的趋肤深度远远小于MT场的趋肤深度.例如,当水深d=50 m,频率f=0.1 Hz和海底介质电导率σ2=0.3 S·m-1时,δMT/δOWEM≈120,说明海浪感应电磁场在海底介质中的衰减速度为MT场的120倍.
2.2 阻抗
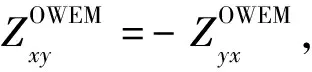
图5为海浪感应电磁场阻抗振幅与相位和MT场阻抗振幅和相位对比.MT场阻抗的振幅不受水深的影响,并且TM极化模式下其阻抗的相位为135°固定不变(图5b和5d黑线).由图5a可知,当水深和频率一定时(如水深d=50 m,频率f=0.1 Hz),MT场阻抗振幅随着海底介质电导率的增加而减小,但海浪感应电磁场阻抗振幅基本不受海底介质电导率的影响.当海底介质电导率和水深一定时(如σ2=0.3 S·m-1,水深d=50 m),海浪感应电磁场阻抗振幅随着频率的增大而减小.当海底介质电导率和频率一定时(如σ2=0.3 S·m-1,频率f=0.05 Hz),海浪感应电磁场阻抗振幅随着水深增大而增大(图5e).海浪感应电磁场阻抗的相位受海底介质电导率、频率和水深的影响非常小,约为90°(图5b,5d和5f),偏差小于0.06°.可以得到海浪感应电磁场和MT场的两种极化方式下阻抗的特征如表1所示.
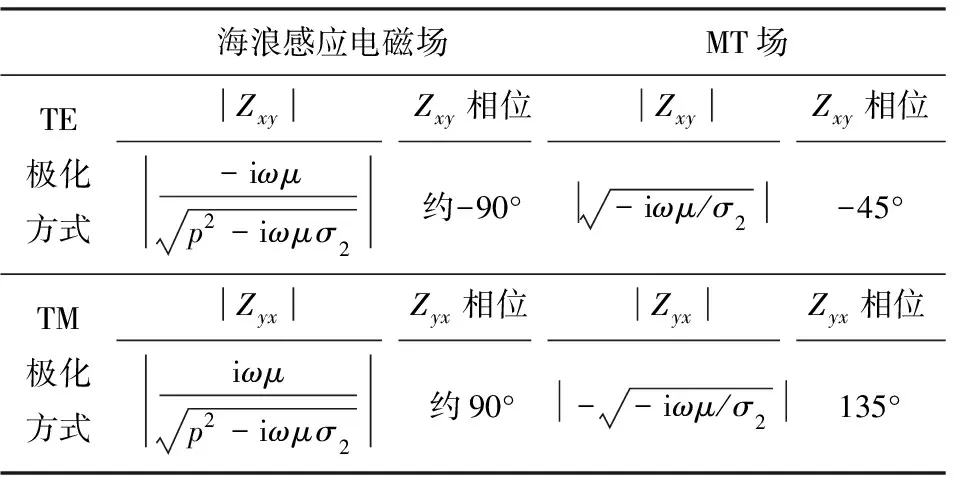
表1 三层海洋地电模型海浪感应电磁场和MT场的阻抗特征Table 1 The impedance characteristics of OWEM fields and MT fields in a three-layer ocean geoelectric model
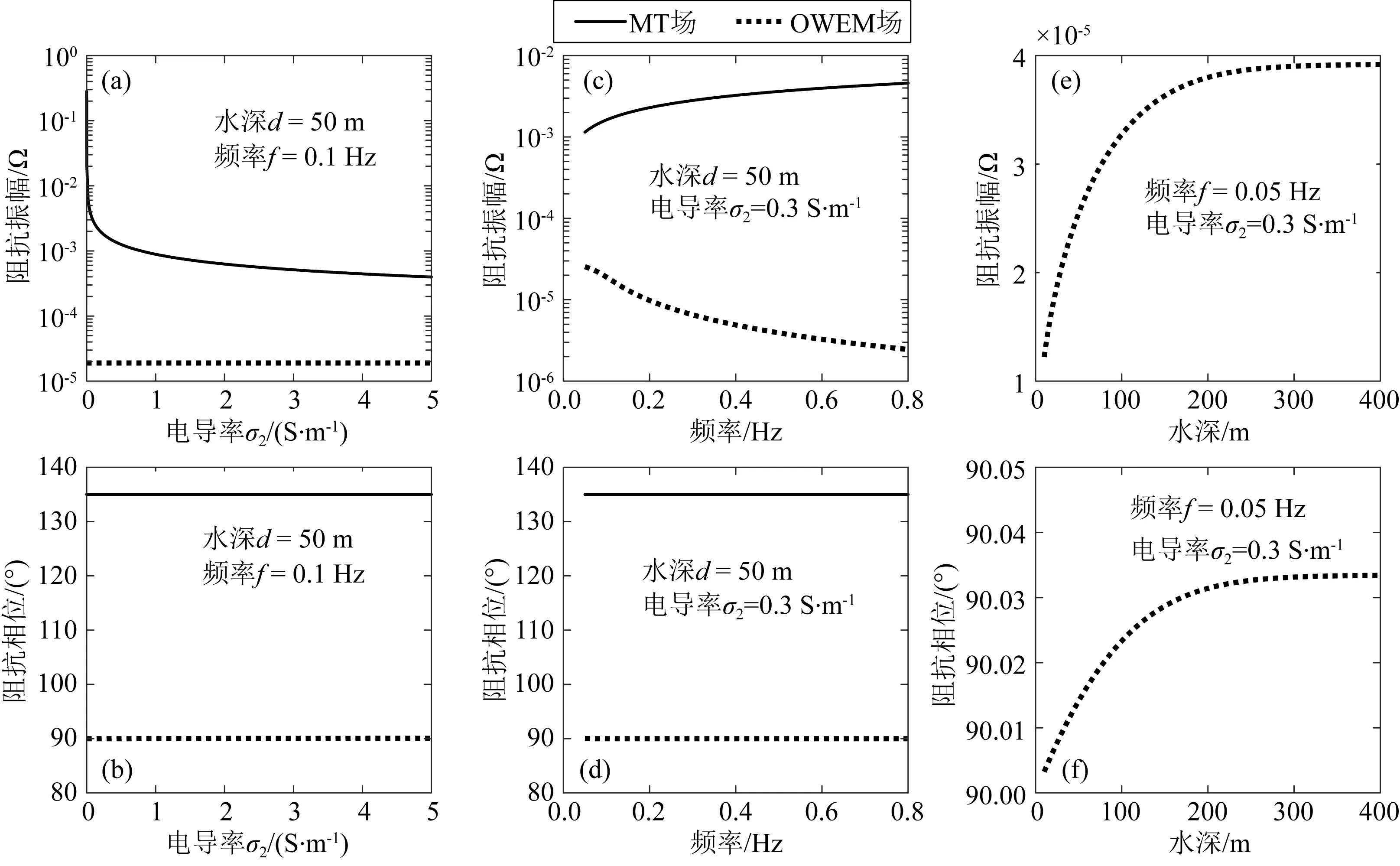
图5 海浪感应电磁场和MT场的阻抗对比 阻抗振幅与海底介质电导率(a),频率(c)和水深(e)的关系;阻抗相位与海底介质电导率(b),频率(d)和水深(f)的关系.Fig.5 The impedance comparison of OWEM fields and MT fields The relationship between the impedance amplitude and the conductivity of the medium below the seafloor (a), frequency (c), and water depth (e); The relationship between the impedance phase and the conductivity of the medium below the seafloor (b), frequency (d), and water depth (f).
同时,由图5a和图5c可知, MT场阻抗幅值远大于海浪感应电磁场的阻抗幅值,即满足以下关系:
(19)
由式(19)可得:
(20)
式(20)表明,海浪感应磁场对地球变化磁场的影响远大于海浪感应电场对大地电场的影响.
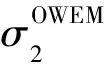
(21)
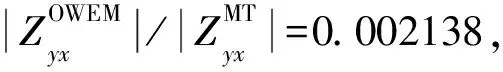
3 复合阻抗特征分析
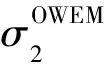
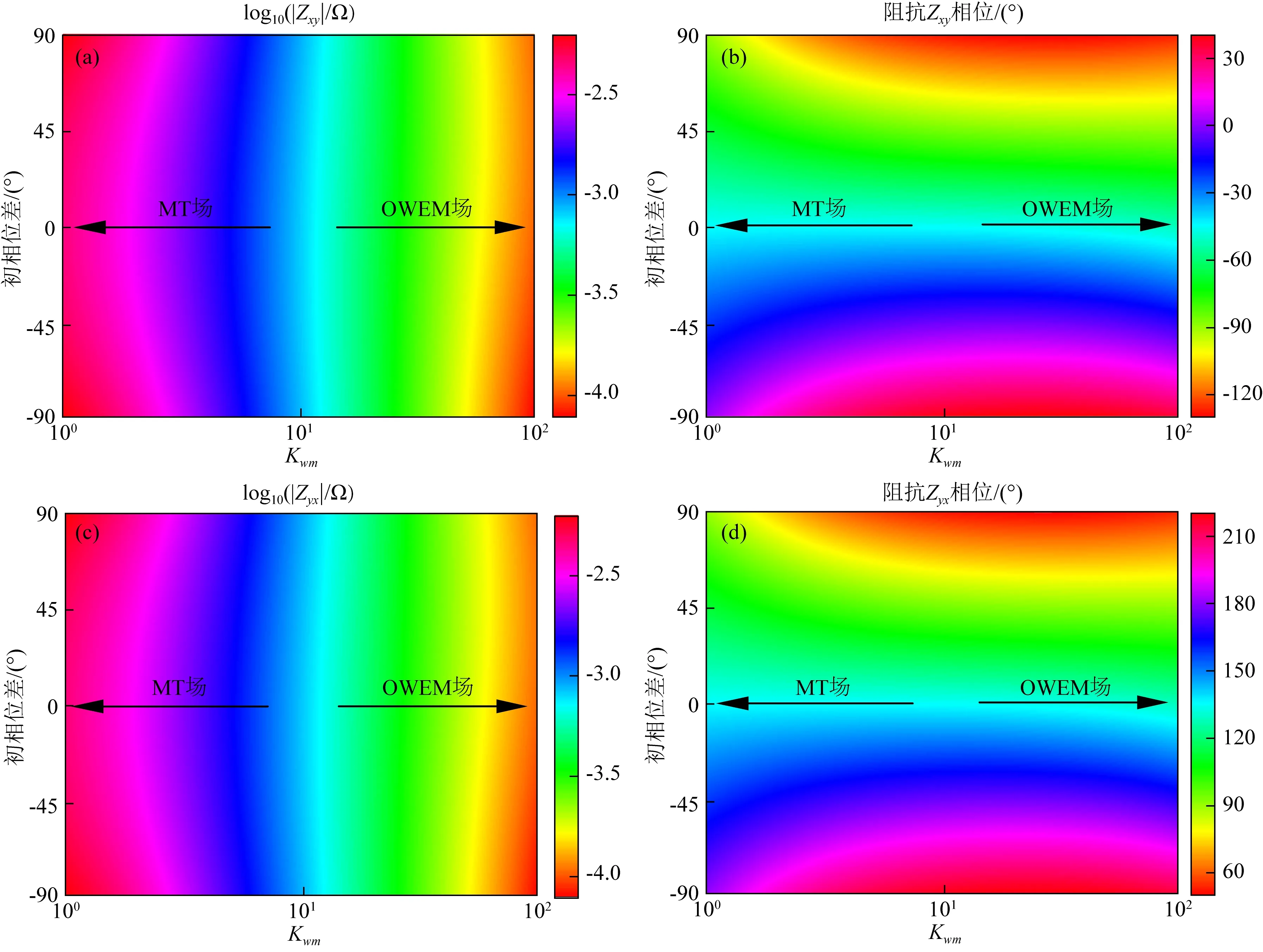
图6 复合阻抗 (a) log10|Zxy|; (b) Zxy的相位; (c) log10|Zyx|; (d) Zyx的相位Fig.6 Composite impedance (a) log10|Zxy|; (b) the phase of Zxy; (c) log10|Zyx|; (d) the phase of Zyx
由图6可知,对于TE和TM极化方式,复合阻抗幅值相等,即|Zxy|=|Zyx|,且复合阻抗相位等值线形态相似,大小相差180°.复合阻抗的幅值和相位都随Kwm减小而逐渐趋近MT场阻抗的幅值和相位,而随Kwm增大而逐渐趋近海浪感应电磁场阻抗的幅值和相位.复合阻抗幅值受初相位差φwm的影响较大,它可以使阻抗幅值产生约41%的相对误差,相位相对误差范围±65°,这意味着海浪电磁干扰与海洋MT场叠加增大了阻抗估计结果的不确定性.
实际上,MT数据处理中,单个频点电磁数据的处理通常采用多窗口加权最小二乘法(即robust估计方法;Chave and Thomson,1989,2003,2004;Egbert and Livelybrooks,1996;Bellio,2007)进行阻抗估计.该方法的作用是可以令φwm→0°,同时也减小Kwm,从而使阻抗估计结果趋近于MT场的阻抗.然而,实际数据处理中,由于海浪感应磁场的影响较大,robust估计方法对噪声的压制效果并不理想,最终使得MT场的阻抗估计产生较大偏差.图7展示图6中初相位差φwm=0°时的复合阻抗曲线.
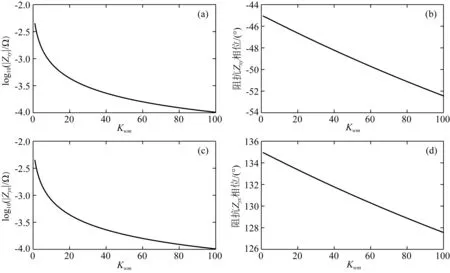
图7 复合阻抗(φwm=0°) (a) log10|Zxy|; (b) Zxy的相位; (c) log10|Zyx|; (d) Zyx的相位Fig.7 Composite impedance (φwm=0°) (a) log10|Zxy|; (b) the phase of Zxy; (c) log10|Zyx|; (d) the phase of Zyx
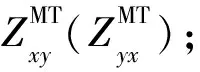
4 结论
本文基于三层海洋地电模型推导了海浪运动感应电磁场表达式.基于海浪感应电磁场平面波传播特征,推导出了海浪感应电磁场趋肤深度和阻抗表达式.通过对比海浪感应电磁场和海洋MT场趋肤深度的特征发现,虽然海浪运动切割地磁场可以在海底产生磁场强度数十倍于地球变化磁场的感应磁场,但由于海浪感应电磁场在海底介质中的衰减速度要比MT场的衰减速度大约快2个量级,因而海浪感应电磁场不能用于探测海底深部电性结构.海浪感应电磁阻抗幅值比MT阻抗幅值小2~3个量级.因此,虽然在浅水区海底处海浪感应磁噪声强度比地球变化磁场强度大1~2个量级,其对地球变化磁场的影响较大,但海浪感应电噪声强度仅约为大地电场强度的10%,其对大地电场的影响较小.在海底介质为均匀半空间的情形下,海浪感应电磁阻抗相位比MT阻抗相位小约45°,偏差小于0.06°.利用海底处电场数据以及附近陆地台站磁场数据(不受海浪感应磁噪声干扰)进行阻抗估计,可以改善海浪运动频带内MT阻抗估计的效果.
致谢感谢匿名审稿专家提出宝贵的修改意见.
附录
将正文式(3)中电流密度J写为矢量形式:
(A1)
其中,Jx、Jy和Jz分别表示x、y和z方向上的电流密度.令
(A2)
其中,J1表示xz平面的电流密度,J2表示y方向的电流密度.
对J1,在海水层中,由斯托克斯公式可得:
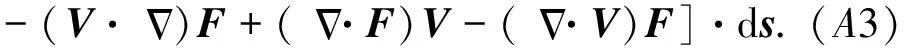
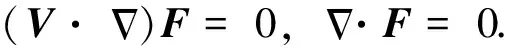
(A4)

对J2,由式(3)可得:
(A5)
由式(A5)可得:
(A6)
对于均匀层状地电模型,海浪速度场、感应电场和感应磁场可以写为
(A7)
由式(3)和式(A7)可得:
(A8)
将海浪速度场式(5)和地磁场式(4)代入式(A8)可以得到:
(A9)
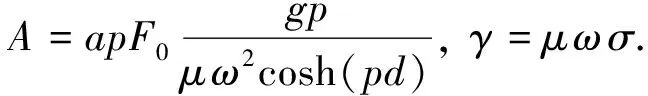
在空气层中(z<0),由于空气层电导率为0,即得γ=γair=0.于是,由式(A9)可得:
d2h/dz2=p2h,z<0
(A10)
在海底介质中(z>d),由于没有海水质点运动,即v=0.由式(A9)可得:
d2h/dz2=(p2-iγ2)h,z>d
(A11)
其中,γ2=μωσ2.
在海水层中,γ=γ1=μωσ1,由式(A9)可得海水层垂直磁场hz的微分方程:
+cosh[p(d-z)]sinI),
(A12)
式(A12)的通解表达式为
sinh[p(d-z)]+sinIcosh[p(d-z)]}(A13)
其中,C1,C2为待定系数.
磁场h写为矢量形式:
(A14)
将式(A14)代入式(3)中可得:
(A15)
海浪感应电场表达式为
(A16)
由式(A10)可以得到海水层感应磁场通解为
hz=Q1epz+Q2e-pz,
(A17)
当z→-∞,则hz=0,可得Q2=0,式(A17)可以写为
hz=Qepz,
(A18)
Q1,Q2,Q是待定系数.将式(A18)代入式(A15)可得:
hx=-iQepz.
(A19)
与海水层海浪感应磁场相同的推导方式可以得到海底介质中海浪感应磁场的表达式为
(A20)
R是待定系数.海底介质中海浪感应电场表达式为
(A21)
综上所述,可以得到三层海洋地电模型下的海浪感应电磁场表达式,即正文中公式(7)和(8).
