1970s中期全球气温关联网络结构特征的变化研究

王晓娟, 胡恒儒, 王健, 封国林,3

1 常熟理工学院电子与信息工程学院, 江苏苏州 2155002 扬州大学物理科学与技术学院, 江苏扬州 225002 3 国家气候中心气候研究开放实验室, 北京 100081

0 引言

复杂网络理论近几十年来广泛应用于社会学(Watts and Strogatz, 1998)、地震学(Abe and Suzuki, 2004)、生物学(Ravasz et al., 2002)等领域.近20年来,复杂网络在气候学领域的应用研究方兴未艾.例如:众多学者利用复杂网络的理论来描述复杂气候系统(Tsonis and Roebber, 2004),从宏观整体的角度分析气象格点数据之间的相互作用,并通过网络结构特征量表征这些基本单元是否具有近似的动力学行为特征.Tsonis等(2006)结合复杂网络理论,充分考虑系统内部的正负相关,从宏观整体角度描述气候系统的空间结构,进而为气候系统结构特征研究开辟了新的道路.龚志强等(2008)分别从时间和空间两个角度分析气候要素之间的关联性,构建了温度、气压、相对湿度和纬向风四种气候要素关联网络,比较分析了四种网络时空演变特征的异同.Wang等(2009)分析了中国区域降水和温度场的空间结构特征,发现中国的温度网络具有全局耦合型特征.气候系统复杂网络的优点(龚志强等, 2014)主要表现为:(1)可以保留气候系统的复杂性,(2)有助于分析气候子系统之间的相互关系,(3)有助于从系统结构跃变的角度研究气候突变和相态转变问题等.因此,气候系统复杂网络的兴起为气候系统复杂性研究提供了新思路(Fan et al., 2017; Ludescher et al., 2013; Tsonis and Swanson, 2008; Yuan and Lu, 2020).

IPCC_AR6报告指出,相对于1850—1900年,2001—2020 年这20年平均的全球地表温度升高了0.99℃,2011—2020年10 年平均的全球地表温度已经上升约 1.09℃,比1850年以来的任何一个10年都要暖(翟盘茂等, 2021).全球变暖不仅表现为温度的上升,也表现为全球海温和大气变量自20世纪下半叶以来的不平稳特征(Huang and Wu, 1989),其中最为典型的现象为1976/77年的气候态调整(Huang et al., 2010; Sun et al., 2016).一方面,这段时期冬季热带太平洋海温比正常时期更加温暖,ENSO事件更加频繁地发生,出现了一系列更为极端的El Nio事件(Cai et al., 2014; Lee and McPhaden, 2010),对北半球气候乃至全球大气环流产生重要的影响(Agosta and Compagnucci, 2008; Swanson and Tsonis, 2009).另一方面,Tsonis等(2007)揭示了1976/77年冬季“气候过渡”表现为遥相关和厄尔尼诺和南方涛动指数耦合调整.Wang等(2009)发现当北半球主要气候模态达到同步状态并且这些模态之间的耦合强度增强时,气候系统会进入一种全新的状态,且这种气候态的转变伴随着全球增暖趋势的调整以及ENSO变率的变化.Wang等(2012)研究也指出北大西洋涛动与太平洋地区的气候子系统之间的耦合强度增强对应气候态发生相应的调整.由于全球气温升高在一定程度会改变全球气温异常在偏冷年和偏暖年的空间分布,这种变化必然会对以相关性为基础的全球气温网络的构建和结构产生一定的影响(Tsonis and Swanson, 2008),但目前关于这方面的研究似乎还缺少明确的结论.

在上述研究中,我们注意到关于1970s中期的气候态调整研究中,多为气温和降水要素本身或海气指数间的耦合变化研究,但没有详细研究1970s中期之后全球气温系统内部相互作用的时空演化特征及其变化.全球气温关联网络的结构特征在1970s中期是否存在类似气候突变的调整?全球变暖引起的气温序列中蕴含的线性增暖趋势是否会对网络的构建及其结构特征有一定程度的影响?关于这两个科学问题的研究相对较少,且缺少明确的结论.因此,本文基于全球地表气温再分析资料,分别构建了偏冷态和偏暖态对应的气温关联网络,揭示了1970s中期网络结构的时空演化特征,探究网络结构特征发生调整的可能成因,简析了全球变暖趋势对于全球气温关联网络结构特征变化的可能影响.文章第二部分介绍了方法和数据,第三部分介绍了主要的分析和结果,最后给出了本文的主要结论和简要讨论.

1 数据和方法

1.1 数据

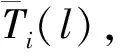
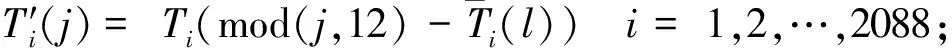
j=1,2,…,852;l=1,2,…,12

(1)

其中mod为相对于12的取余数函数.采用了NOAA数据集中1891—2020年空间分辨率为1°×1°的月均海表温度数据集(https:∥psl.noaa.gov/data/gridded/data.cobe.html).文中每月Nio3.4指数数据来自NOAA地球系统研究实验室(https:∥psl.noaa.gov/gcos_wgsp/ Timeseries/Nino34/).

1.2 构建全球气温关联网络的气温序列提取

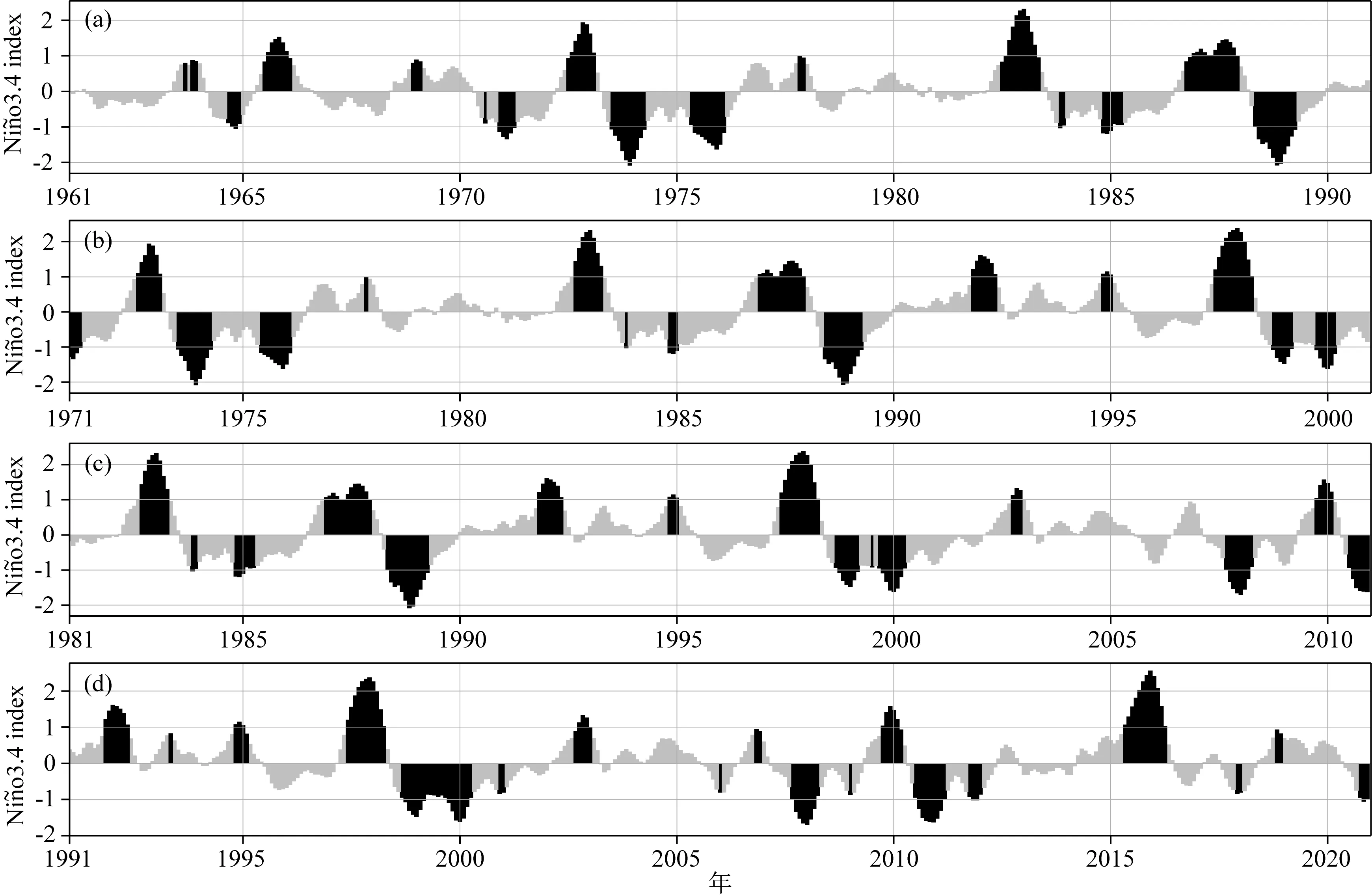
图1 逐月Nio3.4指数序列(a)—(d) 分别对应不同30年滑动窗口内的Nio3.4指数序列,深色负值和正值分别代表偏冷态和偏暖态的50个月气温序列, 灰色表示正常态的月份.Fig.1 Monthly Nio 3.4 index(a)—(d) Index in each 30-year smooth window. The dark negative and positive values represent the cold phase and the warm phase, while the grey represents the normal months.

1.3 全球气温关联网络的构建

将全球2088个气温序列格点定义为网络的节点(图2),根据(3)式计算30年滑动窗口内偏冷态和偏暖态对应格点气温序列之间的相关系数.格点之间的相关系数绝对值不小于固定阈值则定义为格点间存在网络连边,进而分别构建偏冷态和偏暖态对应的气温关联网络(Gong et al., 2011; Lu et al., 2018).结合以往的研究,相关系数阈值取为0.5.相关阈值的选取主要考虑了两方面的因素:(1)时间序列长度为50,在N=50的t检验中,相关系数大于0.5满足0.001信度;(2)0.5也是以往构建气温关联网络常用的相关系数阈值(Q)(Tsonis and Roebber, 2004; 胡恒儒等, 2021).

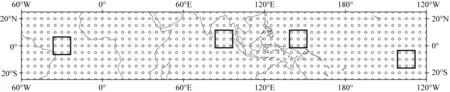
图2 全球气温关联网络中四个大洋关键区的节点分布 点表示网络节点,方框分别表示大西洋关键区(5°N—5°S,35°W—25°W),印度洋关键区(10°N—0°,85°E—95°E), 西太平洋关键区(10°N—0°,140°E—150°E),东太平洋关键区(5°S—15°S,140°W—130°W).Fig.2 Key region of the global temperature correlation network Points indicate the network points; boxes indicate the selected key regions; key region of Atlantic (5°N—5°S,35°W—25°W), Indian Ocean (10°N—0°,85°E—95°E), West Pacific (10°N—0°,140°E—150°E), and East Pacific (5°S—15°S,140°W—130°W).

关联矩阵理论的主要思想如下:对于一个M维,长度为N的多变量数据集合Xi(t).首先我们对原始数据作标准化处理:

(2)

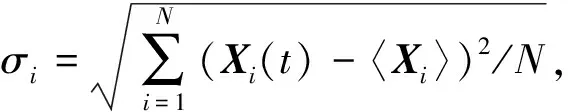
(I=1,…,M-1;j=i+1,…,M),

(3)

其中,M为网络中格点个数,N为网络格点对应的序列长度.构建全网络时,N=852,构建偏冷态度和偏暖态网络时N=50.每一个相关系数Cij的范围为-1≤Cij≤1,Cij=1表示完全正相关,Cij=-1表示完全负相关,Cij=0表示不相关.

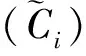
(4)

其中,latj为与节点i有连边的节点j的纬度.连通度值越大,表示该节点在网络的作用越强,对网络的影响也越大.网络平均联通度越大,则表示网络的整体联通性相对较好.

采用网络链路距离(S)来表述气温关联网络的长距离连接顶点之间的关系(Robusto, 1957),计算公式如(5)式:

(5)

其中,lati和latj分别为格点i和j对应的纬度,loni和lonj分别为格点i和j对应的经度,地球半径R=6371 km.网络链路距离平均值越小,则表述网络中长距离连接较多,网络的遥相关作用强.

(6)

全局聚类系数则是所有局部聚类系数的平均值,主要表征网络内部那种“物以类聚,人以群分”的特征.全局聚类系数越大,网络的区域同步性越好,反之则相反.

特征路径长度(L)是度量网络中顶点间的平均最短距离(Albert and Barabási, 2002),即节点i与相互连接的节点j所要经过的最少连边数为最短路径长度Lij.节点对之间最短路径长度的平均值为网络特征路径长度,计算公式如(7)式:

(7)

特征路径长度越小,说明任意两个节点之间建立联系需要经历的中间过程越短,网络内部信息的传递效率则越高.

Fan等(2017)究表明,连通度最高的区域主要位于低纬度海洋,且网络节点的连通度越高,该节点对网络结构的影响则越强.为避免面积不均匀造成不必要的影响,本文选取的四个大小一致,且对应网络联通度较高的关键区域(图2).

2 主要研究结果

2.1 全球气温关联网络连通度的演化特征

图3给出了全球气温关联网络的拓扑特征量随时间的演化特征.在1976年之前,偏冷态对应的气温关联网络连通度、集聚系数、链路距离整体都大于偏暖态.在1970s中期之后,偏冷态气温关联网络的连通度、集聚系数、链路距离的值迅速下降,特征路径长度明显上升,造成1970s中期之后全球气温关联网络的连通性偏冷态小于偏暖态.造成这种反转的原因主要是,1970s中期之后偏冷态的气温关联网络连通性迅速减弱,而偏暖态气温关联网络连通性仅略有增强.

图3 全球气温关联网络结构特征量随时间的变化(a) 连通度; (b) 链路长度; (c) 集聚系数; (d) 特征路径长度; (e) 每个时间窗口对应的全球气温距平的平均值. 其中,横坐标表示每个时间窗口的开始年份,实线和虚线分别表示偏冷态和偏暖态.Fig.3 Variation of network structure variable of global temperature correlation network(a) Network connection; (b) Length of network route; (c) Cluster coefficient; (d) Character route length; (e) Average of global temperature anomaly in each 30-year smooth window. Abscissa is the start year of each smooth window. Solid and dash cures represent the cold and warm phase, respectively.

为进一步探究相关系数阈值(Q)选取的可能影响,我们对Q取值0.40,0.45,0.50,0.55和0.60五种情况,分别给出了偏冷态和偏暖态对应的网络连通度的变化曲线(图4).可以看出,随着阈值的增加,网络连通度整体呈现下降的趋势,但在1975年前后气温关联网络结构的调整特征保持不变.因此,阈值升高,网络中满足条件的网络连边减少,会造成网络整体连通性的下降,但这种变化不会改变偏冷态和偏暖态对应网络结构特征的调整.

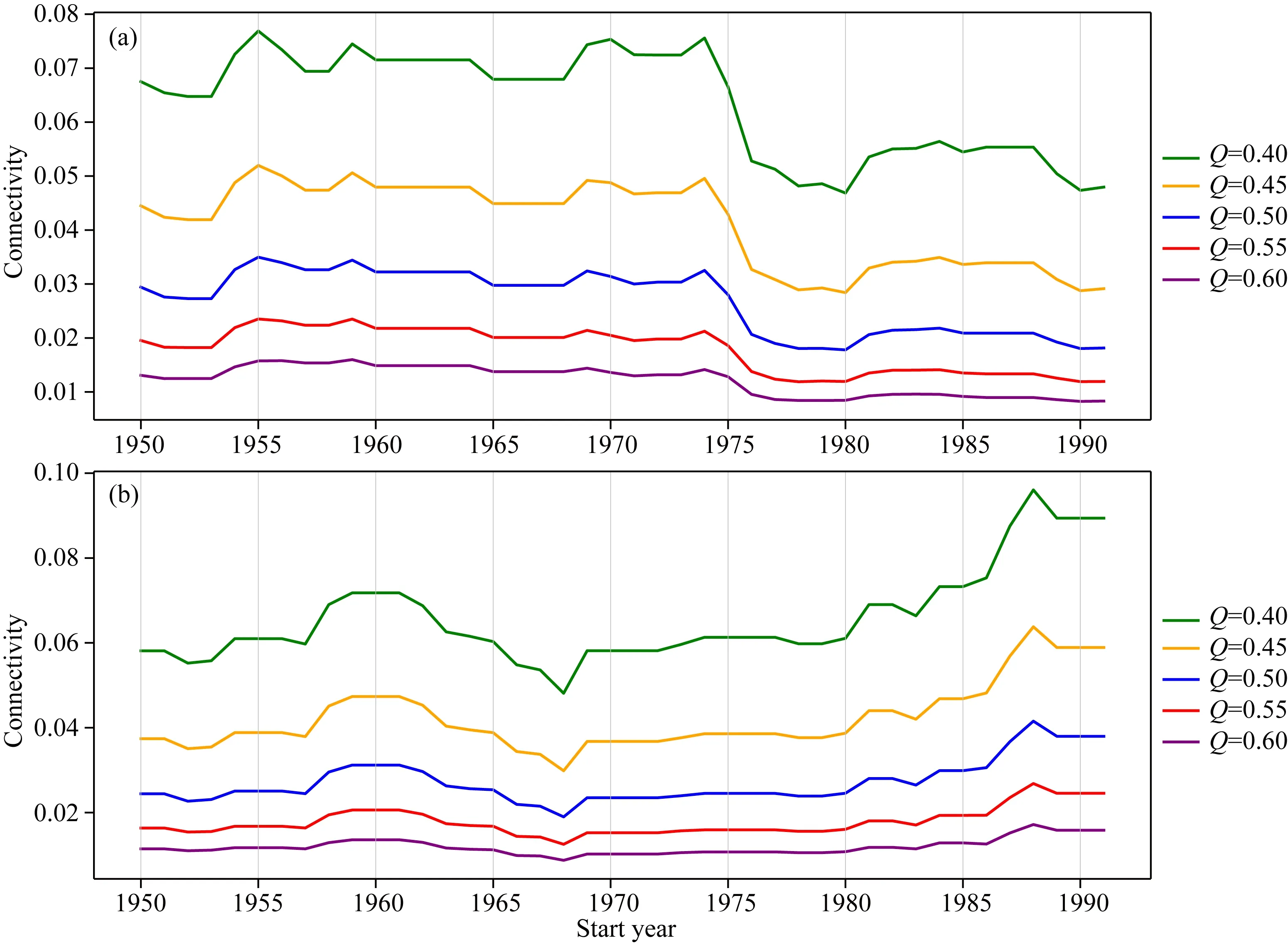
图4 不同相关系数阈值条件下全球气温关联网络连通度随时间的变化(a) 偏冷态; (b) 偏暖态.Fig.4 Variation of network degree of the global temperature correlation network under different correlation coefficient threshold(a) Cold phase; (b) Warm phase.

为了进一步表征和分析1970中期网络结构特征量的变化特征,我们选取1950年1月—1976年12月和1977年1月—2000年12月两段,分别构建偏冷态和偏暖态对应的全球气温关联网络.图5给出了1976年前后网络连通度的空间分布.在1976年之后,偏冷态网络的连通度大幅下降,度值异常大的节点区域范围明显减小,而偏暖态网络的连通度略有增加,即偏冷态和偏暖态气温关联网络的连通度大小关系由1976年之前的前者偏强反转调整为后者偏强.连通度变化最大的区域主要发生在赤道区域的大西洋、印度洋、西太平洋和东太平洋区域等.下面结合四个关键区域连通度的变化,进一步分析气温关联网络连通性发生转变的可能原因.

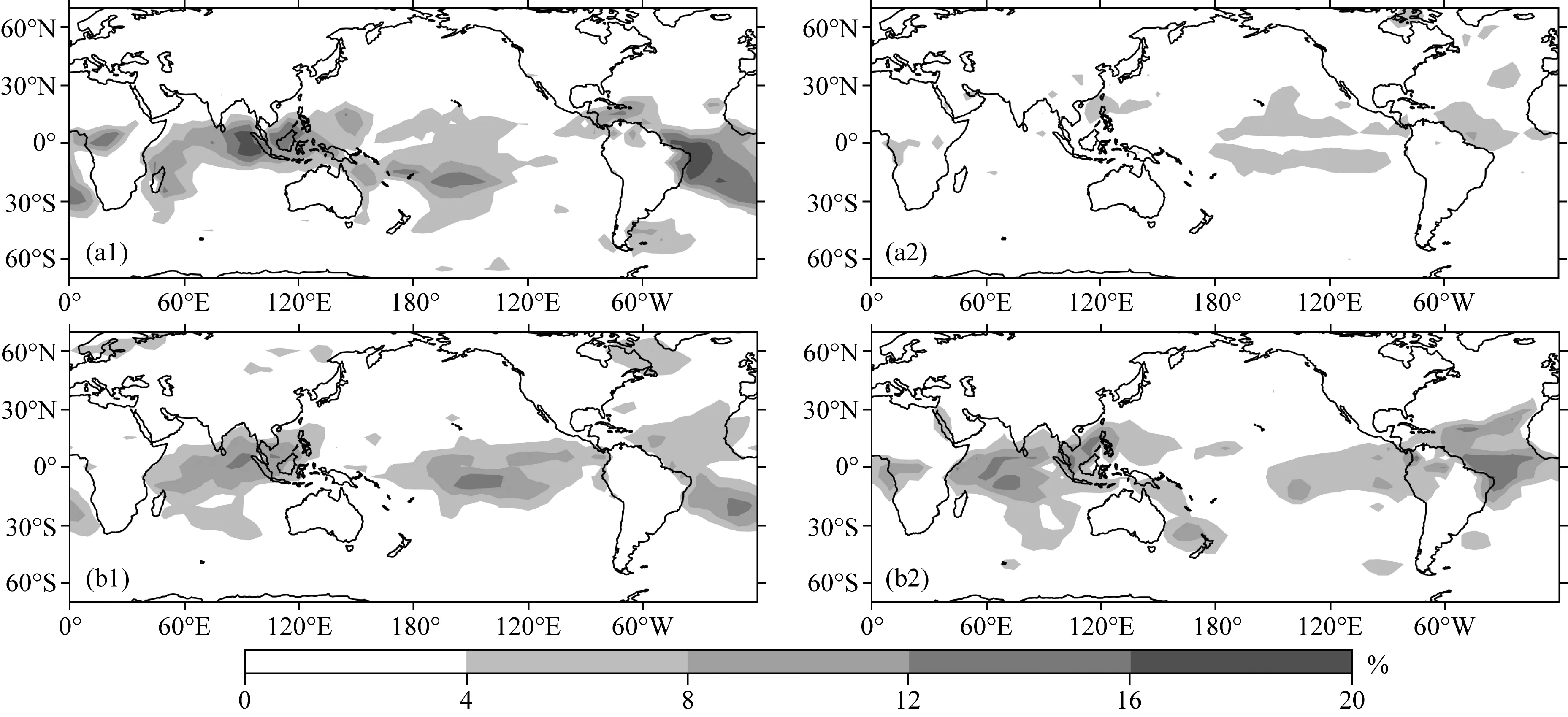
图5 偏冷态和偏暖态气温关联网络在1976年前后网络连通度的空间分布(a1) 偏冷态1950—1976年; (a2) 偏冷态1977—2000; (b1) 偏暖态1950—1976年; (b2) 偏暖态1977—2000.Fig.5 The spatial distribution of network connectivity of cold and warm phase corresponded temperature correlation network before and after 1976(a1) Cold phase, 1950—1976; (a2) Clod phase, 1977—2000; (b1) Warm phase, 1950—1976; (b2) Warm phase, 1977—2000.

2.2 全球气温关联网络连通性调整的成因分析

2.2.1 大洋关键区之间的气温相关性变化

气温关联网络的构建基于皮尔逊相关系数,相关系数的大小直接决定了网络连边的数量,从而直接影响网络内部结构特征.图6给出了四个关键区之间气温距平序列相关系数的变化.可以看出,偏冷态对应各大洋关键区之间的相关系数,在1970s中期之后迅速下降.偏暖态时期各大洋关键区之间的相关系数在1970s中期之后保持稳定.1970s中期之后偏冷态和偏暖态网络特征连通度强弱关系发生反转的直接原因是在偏冷态对应的大洋关键区气温序列间的相关系数减弱,而偏暖态时期略增加.

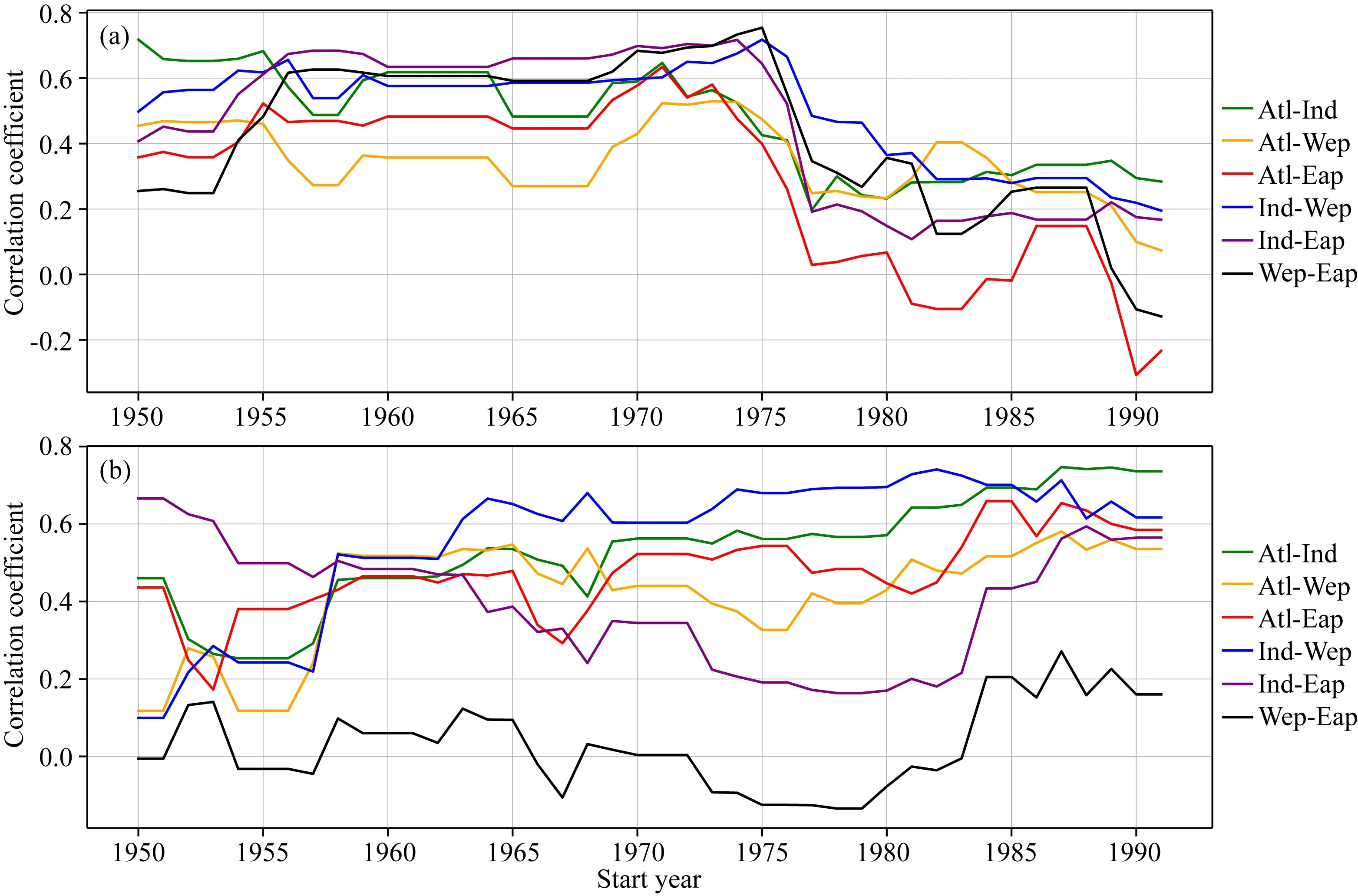
图6 各大洋关键区之间平均气温距平序列相关系数随时间的演化(a) 偏冷态; (b) 偏暖态.图中,大西洋与印度洋(绿)、西太平洋(黄)、东太平洋关键区(红)之间的相关系数, 印度洋与西太平洋(蓝)、东太平洋(紫)以及东太平洋和西太平洋(黑)关键区的相关系数演化曲线.Fig.6 The evolution of correlation coefficients of temperature anomalies among different key regions(a) Cold phase; (b) Warm phase. Correlation between Atlantic and Indian Ocean (green cure), West Pacific (yellow cure), East Pacific (red cure); Correlation between Indian ocean and West Pacific (blue cure), East Pacific (purple cure); correlation between East Pacific and West Pacific (black cure).

2.2.2 相关系数变化的原因分析

下面进一步探究各大洋关键区之间平均气温距平序列相关性变化的成因.皮尔逊相关系数计算公式如公式(8)所示:

(8)

其中,分子为协方差,分母为标准差乘积.图7给出了各大洋关键区气温距平序列之间的协方差随时间的演化.可以看出,协方差随时间的演化趋势与图6中相关系数随时间的变化趋势基本一致,但是幅度上更大一些.在偏冷态时期很多大洋关键区之间的协方差下降为五分之一,其中大西洋与东太平洋和西太平洋与东太平洋关键区之间的协方差甚至下降到了零值附近.与此同时,分母标准差乘积的变化则不明显(图略).因此,各大洋关键区气温序列之间协方差的调整是引起偏冷态时期相关性大幅下降的直接原因.

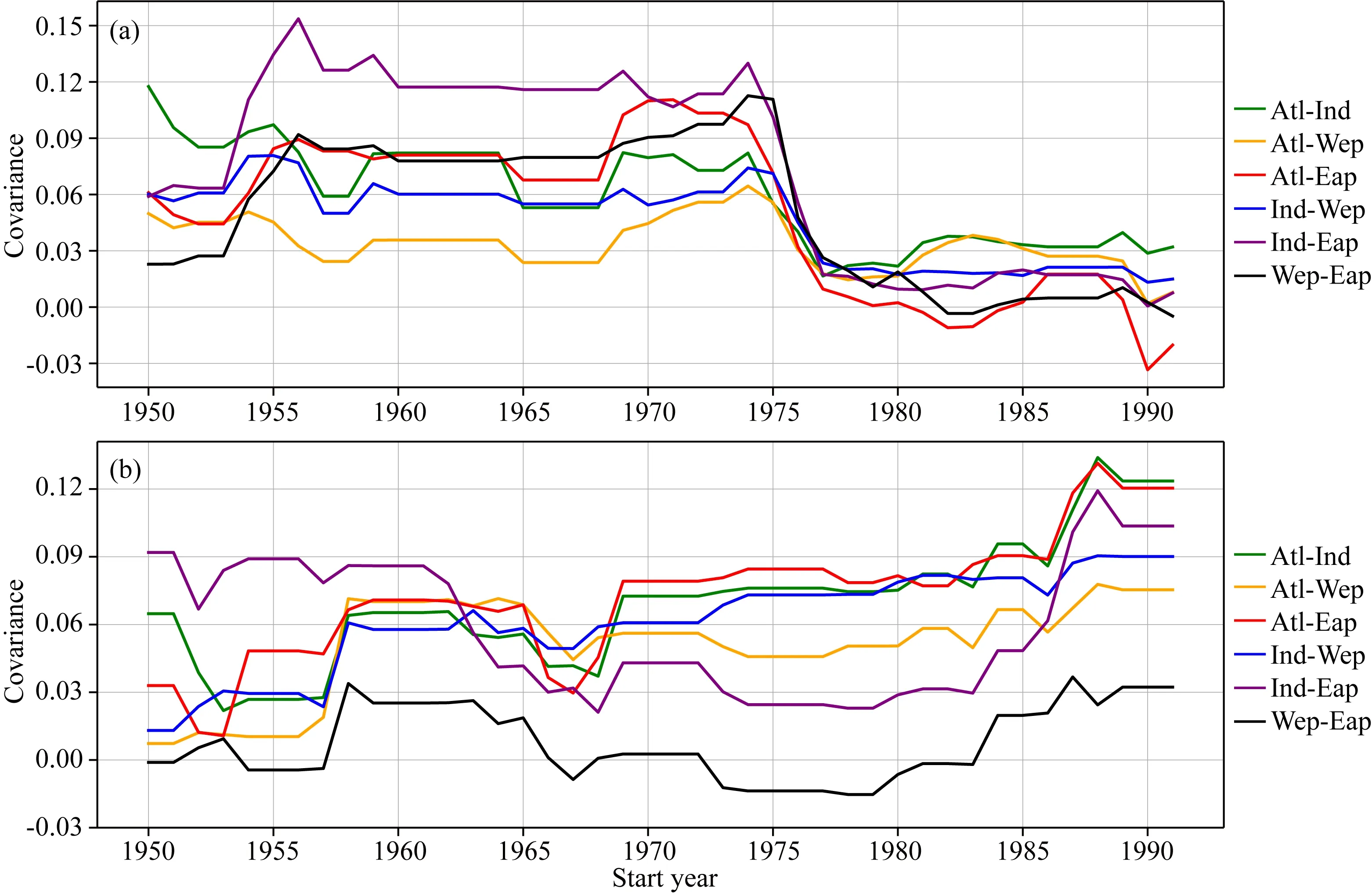
图7 各大洋关键区之间气温距平值协方差随时间的演化(a) 偏冷态; (b) 偏暖态.图中大西洋与印度洋(绿)、西太平洋(黄)、东太平洋关键区(红)之间的协方差, 印度洋与西太平洋(蓝)、东太平洋(紫)以及东太平洋和西太平洋(黑)关键区的协方差.Fig.7 The evolution of covariance of temperature anomalies among different key regions(a) Cold phase; (b) Warm phase. Covariance between Atlantic and Indian Ocean (green cure), West Pacific (yellow cure), East Pacific (red cure); Covariance between Indian ocean and West Pacific (blue cure), East Pacific (purple cure); Covariance between East Pacific and West Pacific (black cure).

图3e给出了每个时间窗口对应的全球气温距平的平均值.全球气温呈现一个上升趋势,且全球气温距平在1976年左右经历了一个由负位相转变为正位相的过程.假设这种线性上升趋势会对气温序列间的协方差变化造成一定的影响.为了验证这种假设,给出了各大洋关键区气温距平序列的变化图(图8).可以看出,偏冷态对应大西洋和印度洋关键区气温距平值在1970s中期由负位相变为正位相,西太平洋区域在1958年后就由负转正后,在1976年后正值进一步增大,而东太平洋关键区气温距平持续保持负位相,且1975年后负值略变小.1970s中期关键区正负位相调整对应大西洋—东太平洋、印度洋—东太平洋、西太平洋—东太平洋等区域之间的气温距平值由原来的负-负配置调整为正-负配置,造成这些区域气温序列间的协方差值迅速下降.与此同时,偏暖态对应的主要关键区域的气温距平,在1976s中期以后基本保持正位相,且正值略有增加,关键区域气温序列间的协方差值略微增加.

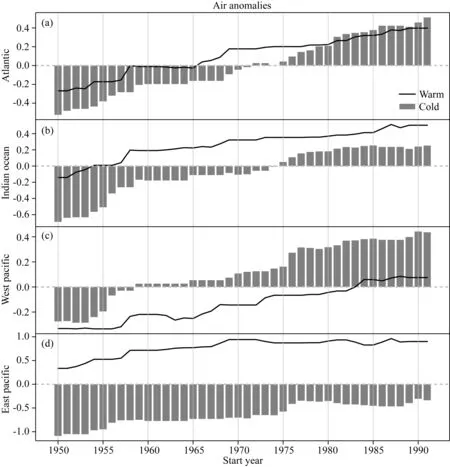
图8 各大洋关键区气温距平的平均值演化图 其中,灰柱代表偏冷态,黑线代表偏暖态. (a)—(d)分别为大西洋、印度洋、西太平洋、东太平洋关键区.Fig.8 The evolution of temperature anomalies of different key regions Gray bars represent the cold phase, black curves represent the warm phase. Key region of (a) Atlantic, (b) Indian Ocean, (c) West Pacific, and (d) East Pacific.

图9给出了不同滑动时间窗口中全球气温距平的空间分布图.偏冷态对应的大西洋、印度洋和东太平洋气温距平在1970s中期之前均为负值,1970s之后则对应大西洋、印度洋调整为正值为主,而东太平洋保持负值(图9),这必然导致关键区域之间的气温序列的协方差大幅下降,相关性降低,引起偏冷态对应气温关联网络的连通度在1970s中期后迅速减小.偏暖态的情况则不同,大西洋、印度洋和东太平洋气温距平在1970s中期始终保持以暖位相为主的特征,引起气温关联网络的连通度略微增加.此消彼长,造成偏冷态和偏暖态气温关联网络的连通度大小关系由1976年之前的前者偏强反转调整为后者偏强.IPCC 报告指出(2021),受全球增暖的影响,全球气温存在不同程度的增加.比如,2011—2020年,地球表面平均温度比19世纪末(工业革命之前)的平均温度高1.1℃.气温升高的同时,必然会造成一些冷异常不太明显的区域的气温距平(相对于1981—2010年平均气温对应气候态)更容易出现正距平.因此,有利于出现大西洋、西太平洋和印度洋等关键区域的气温距平由负相位转变为正相位的变化.但是,对于Nino 3.4指数偏低年对应的偏冷态而言,由于赤道中东太平洋区域海温异常偏低,造成大气温度也异常偏低,全球增暖在一定程度会减弱这种冷态对应气温负距平程度,但还不足以使其由负距平转变为正距平,因此东太平洋关键区气温距平保持负位相.

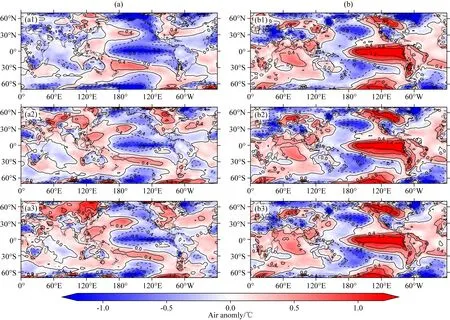
图9 不同滑动时间窗口中全球气温距平的空间分布(a) 偏冷态; (b) 偏暖态; (a1, b1) 对应时间窗口1950—1979年; (a2, b2) 对应1976—2005年; (a3, b3) 对应1981—2010年.Fig.9 Spatial distribution of temperature anomalies in different sliding time windows(a) Cold phase; (b) Warm phase. The time window of (a1, b1) 1950—1979, (a2, b2) 1976—2005, and (a3, b3) 1981—2010.

2.2.3 全球增暖趋势对全球气温关联网络结构特征调整的影响

为了探究全球增暖对全球温度场关联网络的影响,这里对每个格点1950—2020年的温度距平序列分别进行线性拟合,然后从格点的异常值序列中去除线性趋势,得到去趋势温度异常值序列(He et al., 2016).基于去除线性趋势后的气温序列构建气温关联网络,并计算网络结构特征量,以此消除温度增暖趋势的影响.

图10中,去除温度趋势后全球气温关联网络的连通度空间分布型并没有明显的变化,但连通度值较图5明显减弱.全球增暖趋势有助于增强全球气温内部的关联强度,提升气温关联网络的连通性.Fan等(2017)研究也指出,随着气候变暖,气温关联网络中会出现越来越多的长程链接.此外,偏冷态和偏暖态对应的网络联通之间的差异较去趋势以前明显减弱.图11给出了去除全球增暖趋势前后偏冷和偏暖态气温关联网络在1976年前后网络连通度平均值.去除增暖趋势后冷暖态气温关联网络的差异明显减小,两者的总体连通度平均值差异在1976年前由原来的13.1%降到-1.7%,1976年后由原来的-37.0%下降到-8.2%.换而言之,去除温度趋势前,1976年之前偏冷态连通度较偏暖态偏强,1976年之后则转为偏弱;滤除趋势后,1976年之前偏冷态的连通度较偏暖态非常接近,1976年之后偏暖态的联通度略偏强,两者之间的差异明显减小.因此,全球增暖造成的气温线性变化趋势会造成偏冷态和偏暖态对应气温关联网络连通度对比的反转.全球增暖不仅表现为全球气温在1970s左右的距平位相调整,也表现为全球气温关联网络结构特征的变化,这是对已有关于全球增暖影响的新认识.

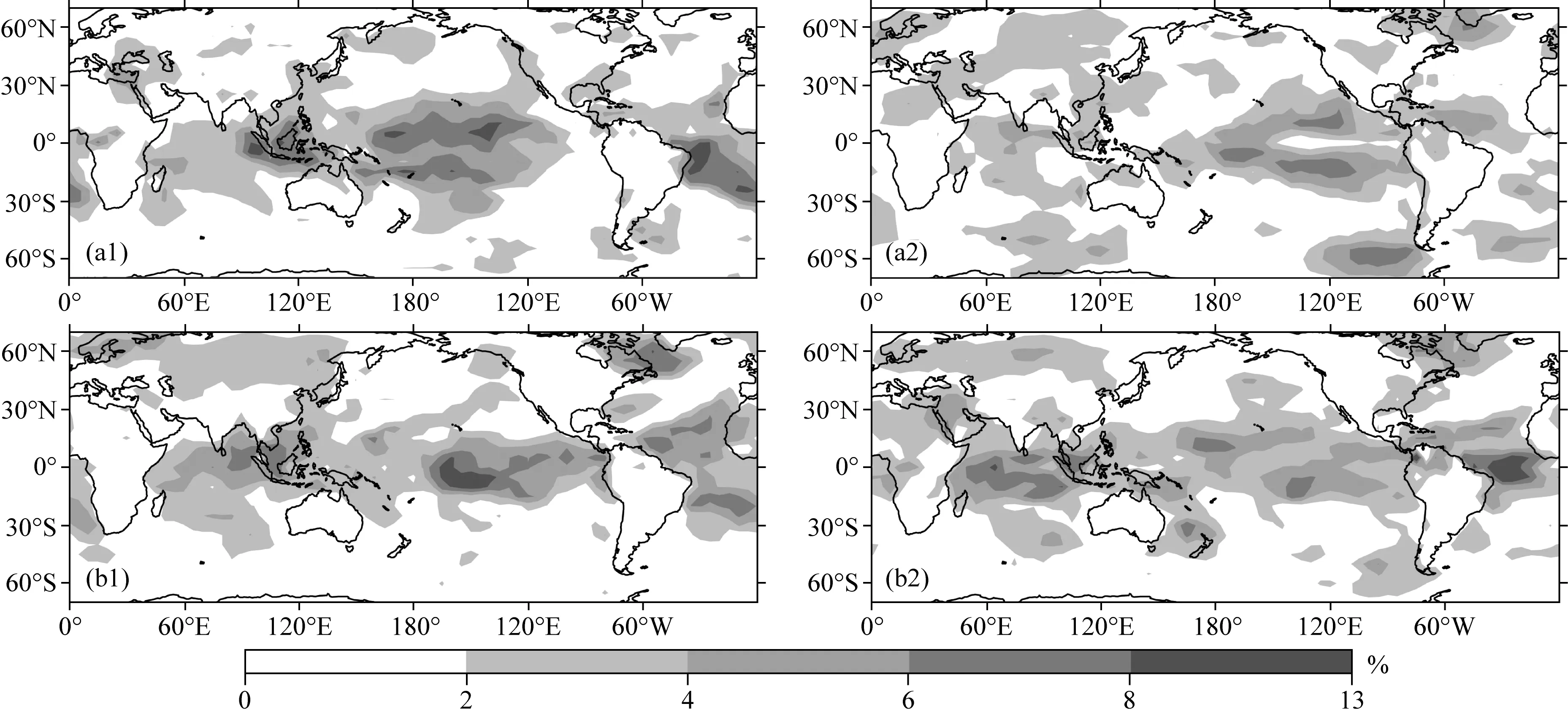
图10 去除线性增暖趋势后偏冷和偏暖态气温关联网络在1976年前后网络连通度的空间分布(a1) 偏冷态1950—1976年; (a2) 偏冷态1977—2000; (b1) 偏暖态1950—1976年; (b2) 偏暖态1977—2000年.Fig.10 The spatial distribution of network connectivity of temperature correlation network after removing the linear warming trend in cold and warm phase(a1) Cold phase, 1950—1976; (a2) Clod phase, 1977—2000; (b1) Warm phase, 1950—1976; (b2) Warm phase, 1977—2000.

图11 去除全球增暖趋势前后偏冷和偏暖态气温关联 网络在1976年前后的网络连通度平均值(a) 未处理的气温关联网络; (b) 去除线性趋势后的气温关联网络.Fig.11 The average of network connectivity of temperature correlation network before (a) and after (b) removing the linear warming trend

3 结论和讨论

本文基于再分析全球表面气温资料,应用30年滑动窗口的方法,分别构建偏冷态和偏暖态对应的气温关联网络.通过计算网络结构特征量,揭示1970s中期全球气温关联网络结构特征的调整,并分析其可能的成因.主要研究结论如下:

在1970s中期之后,全球气温关联网络在偏冷态网络中的连通度大幅下降,度值异常大的节点区域范围明显减小,而在偏暖态网络中的连通度略有增加;此消彼长,造成偏冷态和偏暖态气温关联网络的连通度大小关系由1976年之前的前者偏强调整为后者偏强,且这种变化最为显著的区域位于热带的四个大洋关键区.

偏冷态对应各关键区之间的相关系数于1970s中期快速下降,而偏暖态时期相关系数则保持稳定,甚至缓慢增加,这是造成网络连通性发生转变的直接原因.在1970s中期,大西洋、西太平洋和印度洋等关键区域的气温距平由负相位转变为正相位,而东太平洋关键区气温距平维持负位相,正负位调整对应成大西洋—东太平洋、印度洋—东太平洋、西太平洋—东太平洋等区域之间的气温距平值由原来的同为负值调整为正-负值配置,造成这些区域气温序列间的协方差值迅速下降.大洋关键区气温序列间的协方差的变化是导致大洋关键区相关性变化的主要原因,即偏冷态时期大洋关键区之间协方差的迅速下降引起相关系数明显下降.与此同时,偏暖态对应的主要关键区域的气温距平,在1970s中期以后基本保持正位相,且正值略有增加,造成关键区域气温序列间的协方差值略增加.1970s中期,大洋关键区气温序列间的偏冷(暖)态协方差减小(略增加),相关系数减小(略增加),造成网络连通度减小(略增加),这是不同ENSO位相对应的全球气温关联网络连通度强弱对比发生反转的主要原因.

去除全球增暖线性趋势后,偏冷态和偏暖态对应的气温关联网络结构特征差异明显减小,两者的连通度平均值差异在1976年前由原来的13.1%降到-1.7%,1976年后由原来的-37%下降到-8.2%.因此,全球增暖不仅表现为全球气温的上升,同时会造成偏冷态和偏暖态对应气温关联网络连通度对比的反转,即造成全球气候系统内部结构的调整.

以往的研究中,有学者提取了全球海表温度场的年代际模态,揭示了1977—1996年的突变模态在大部分海域上存在与前期较为明显的结构特征(肖栋和李建平, 2007).20世纪年代至世纪尺度温度变化的显著信号有准30～50年、准20～30年、准15年等多种时间尺度的振荡,其中北大西洋等区域对应的30～50年振荡在1960年代存在显著的调整,而北太平洋及其附近地区年平均温度重建的准20～30年振荡分量的演变特征在1970年代中期到80年代初期存在明显的调整(江志红等, 2004).相关研究结果与本文中关于网络结构调整有一定的对应关系,均从气温要素本身出发分析1970s的全球气温突变问题.然而,本文给出了关于全球气温系统内在相互作用的调整分析,是对以往1970s气候突变认识的进一步补充.