去噪算法驱动的地震反演正则化方法

王玲谦, 周辉*, 陈汉明, 李红辉

1 油气资源与工程全国重点实验室,CNPC物探重点实验室,中国石油大学(北京), 北京 102249 2 中国石油东方地球物理公司物探技术研究中心, 涿州 072751

0 引言

地震反演作为地震勘探中重要的定量解释手段,它利用地表观测地震记录和地震正演机制,预测地下介质弹性参数,根据反演得到的弹性参数,可以进一步获得孔隙度、泥质含量等岩石物理参数信息(宗兆云等, 2012; 汪玲玲等, 2017; 郭强等, 2017; 张凌远等, 2021; 印兴耀等, 2020a; 刘军等, 2022; 周林等, 2022; 陈国飞等, 2023).但是,地震反演具有严重的不适定性,主要表现为反演解的不唯一和不稳定.为了获得稳定可靠的反演结果,通常采用正则化方法,使反演结果具有某种期望的特征.常用的正则化方法可以分为确定型和统计型两类.在确定型正则化方法中,通过L2范数正则化获得连续平滑的弹性参数反演结果(Tikhonov, 1963),全变分正则化获得具有块状分布特征的地下弹性参数(Gholami, 2015),通过L1范数、Lp范数、L1-2范数重构地下稀疏的反射系数序列进行稀疏脉冲反演(Zhang et al., 2013; 曹静杰, 2016; Wang et al., 2018).此外,近些年发展了许多自适应的确定型地震反演方法,通过自适应地提取构造特征来约束反演结果(张宏兵等, 2007; She et al., 2018, 2019; 印兴耀等, 2020b; Wang et al., 2021b).在统计型正则化中,基于贝叶斯理论,利用观测记录不匹配项构建似然函数,结合不同的统计模型来定量表示待反演参数的先验信息并用于地震反演,主要包括基于高斯分布的平滑模型反演、基于柯西分布的稀疏反射系数重构、基于混合高斯分布的自适应多岩相地震反演等(Buland and Omre, 2003; Grana and Rossa, 2010; Alemie and Sacchi, 2011; Grana et al., 2017; De Figueiredo et al., 2019).在确定型和统计型正则化中,大部分方法起源于信号和图像处理,基于地震褶积正演模型的线性化假设,这些方法可以很好地结合到地震反演问题中,并取得了预期的效果.但是,许多去噪方法非线性强,难以灵活地应用于地震反演.

在地震数据去噪的研究中,期望在不损害有效信号的同时,恢复出无噪声干扰的地震记录,为后续储层预测提供可靠数据(刘洋等, 2017).在过去的几十年里,学者们提出了许多去噪方法,利用地震记录有效信号的可预测性,构建预测滤波器来去除噪声干扰,包括正向、反向预测技术(Wang, 1999)、f-x反褶积(Naghizadeh and Sacchi, 2012; 国胧予等, 2020)、t-x预测滤波(Abma and Clearbout, 1995)、非稳态自动回归(Yang et al, 2014; Wu et al., 2016)等.有学者研究利用统计信息去除地震记录中的高斯白噪声和脉冲噪声的均值滤波方法(刘财等, 2007; 刘洋等, 2011; 王伟等, 2012).基于分解的方法将含噪数据分解为不同成分,通过选择信号的主要成分达到去除噪声的目的,这些方法包括奇异值分解方法(Bai et al., 2018)、经验模态分解(Chen et al., 2016)、连续小波变换(Mousavi et al., 2016a)、形态学分解(Huang et al., 2017)和低秩分解法(Kumar et al., 2015)等.基于稀疏变换的方法,首先将地震数据转换到稀疏域,通过阈值函数处理稀疏系数,最后将稀疏系数反变换到时空域(Fomel and Liu, 2010; Yuan et al., 2015, 2017).稀疏变换方法可以分为解析法和学习方法两种(Rubinstein et al., 2010).在解析法中,利用已知的数学性质构建数学模型,可以得到基于数学模型的解析解,这些数学模型包括傅里叶变换(Naghizadeh and Sacchi, 2012)、拉东变换(Xue et al., 2014)、小波变换(Mousavi and Langston, 2016)、曲波变换(Hennenfent et al., 2010; Zu et al., 2016)等.这些解析的稀疏变换具有高度的结构化,并且可以快速地实现,但缺乏适应性,难以有效去除观测数据的噪声干扰.基于学习类的去噪方法采用机器学习,从一系列样本中训练数学模型.与解析方法相比,学习类方法可以自适应提取有效信号的特征(Beckouche and Ma, 2014; Siahsar et al., 2017; Zu et al., 2019).

随着地震去噪方法的不断成熟,将其应用到其他反问题的求解中,可以进一步提高去噪方法研究的适用性和研究价值.近些年,已经有许多将图像处理中的滤波类方法应用到地震反演问题的研究(She et al., 2018, 2019; Wang et al., 2021b; 王竟仪等, 2023).Dai等(2019)将保边平滑滤波应用到地震叠后波阻抗反演中,通过对每次迭代输出的弹性参数模型进行保边平滑滤波,提高反演结果的稳定性,并且凸显出边界信息.He等(2020)将块排列平滑滤波应用到多尺度弹性波全波形反演中,对每一次反演结果进行采样点重排列和分段平滑滤波,提高反演结果的抗噪性.Wang 等(2021a)推导出了块排列平滑滤波的正则化形式,该正则化策略是线性的,与褶积正演模型结合,可以通过常用的迭代类算法进行线性求解.虽然,许多去噪类方法已经成功应用到地震反演问题的求解中,但依旧存在许多问题.主要包括,很多去噪算法无法写出具体的表达形式,而且迭代滤波的反演方法会使反演结果难以满足观测地震记录.此外,虽然上述研究通过对一些现有去噪算法进行调整,构建了线性的正则化约束项,但不适用于非线性的滤波算法,不具备灵活性和通用性.

综合去噪类算法引入到地震反演中的尝试和存在的问题,本文提出一种去噪算法驱动的地震反演正则化方法,该方法可以将去噪算法灵活地结合到地震反演正则项的构建中,通过限定去噪算法服从齐次性性质,直接推导出目标函数的梯度形式,利用传统的共轭梯度法进行求解.由于该方法是以拉普拉斯正则化为基础,因此属于确定型正则化方法.在模型测试和实际数据测试中,分别采用非局部均值滤波(Non-Local Mean, NLM)和字典学习(Dictionary Learning, DL)去噪算法,构建相应的正则项.在合成数据和实际数据测试中,与传统的迭代滤波反演方法比较,证明所提出的去噪算法驱动的地震反演正则化方法的可靠性和实用性.

1 基本原理

1.1 叠后地震波阻抗反演

基于褶积正演模型,叠后观测地震记录y可以表示为

y=WDx,

(1)

(2)

其中,ρ(x)表示先验信息约束,λ表示超参数,用于控制先验信息对反演结果影响的权重,反演结果具备的特征取决于先验约束ρ(x)的选取.因此,正则化项的确定一直是地震反演中备受关注的问题.目前常用的正则化方法包括平滑约束、全变分约束、稀疏约束等.基于反演结果偏差与真实模型呈正交关系的假设条件,本文采用拉普拉斯正则化,并将去噪算法作用后的结果作为真实模型,构建去噪算法驱动的正则项:

(3)

其中,去噪算法f(g)应用到待反演参数x上.该正则项正比于对数波阻抗x和去噪算法去除的残差[x-f(x)].在目标函数(2)中,通过求取目标函数极小值确定反演结果,保证观测记录不匹配项和正则项之和最小.对于去噪算法驱动的正则项(3),要使得其数值较小,有两种方式.一种是待反演参数x接近去噪处理后的结果f(x),即x≈f(x).另一种是反演结果的残差[x-f(x)]与反演结果x的互相关较小.

为了便于后续目标函数(2)的求解,本文基于去噪算法f(g)满足齐次性条件进行目标函数的求取,即去噪算子满足:

f(cx)=cf(x).

(4)

为了减弱齐次性条件的硬性约束,本文假设当去噪算法在|c-1|≤ε时满足等式(4),就认为去噪算法具有齐次性,其中ε为较小的阈值,即当c接近于1时满足齐次性条件.该性质用于目标函数对反演的参数x的求导运算.去噪算法作用后的结果f(x)对x的导数可以表示为

(5)

(6)

因此,去噪算法处理的结果f(x)可以表示为

(7)

1.2 目标函数求解

结合目标函数式(2)和去噪算法驱动的正则化项式(3),可以得到基于去噪算法正则化的目标函数:

(8)

该目标函数的梯度为

(9)

基于去噪算法的齐次性式(7),目标函数的梯度可以更新为

(10)

可以看到,基于去噪算法齐次性条件,简化了原目标函数的梯度求解,不需要对复杂、非线性的去噪算法求导.目标函数式(8)为常规的线性方程组的极小化问题,本文采用共轭梯度算法进行求解,算法伪代码如算法1所示.

1.3 性质分析

去噪算法驱动的地震反演正则化方法,可以有效结合常规的去噪算法.当去噪算法满足齐次性条件时,可以利用梯度下降类算法直接求解.常规的去噪算法如均值滤波和保边平滑滤波,采用固定窗长和权重系数,属于线性运算,满足齐次性性质,因此可以直接代入构建的地震反演正则化项中.为了验证所提出方法的有效性,本文采用目前常用的非局部均值滤波(NLM)和字典学习(DL)去噪算法,并验证它们满足齐次性性质.

非局部均值滤波方法采用变权重系数加权平均,属于非线性滤波方法,需要进一步证明其满足齐次性条件.基于NLM的去噪算法可以表达为

f(x)=Q(x;σ)x,

(11)

其中,Q为滤波器的权重值,σ为滤波器的超参数,用于控制局部弹性参数x的相似性对滤波器权重系数的影响.由于滤波器的权重系数与弹性参数x有关,因此该去噪算法属于非线性算法.欲获得第j个采样点的滤波结果,使用第i个采样点处对应的弹性参数值,其对应的滤波器权重值为

(12)

其中,

(13)

(14)

其中,Rix为点i处对应的数据块,j为待求点位置,n表示滤波的采样点个数,标准化算子dj用于保证滤波的权重系数和为

(15)

若使NLM滤波算法满足齐次性条件,需要满足:

f(cx)=Q(cx;σ)(cx)=Q(x;σ)cx=cf(x),

(16)

即需要满足:

Q(cx;σ)=Q(x;σ),

(17)

把比例算子c作用到待反演参数x上,公式(13)中的ei,j可以表示为

(18)

根据泰勒展开,分母可以近似表示为

(19)

将式(19)代入到式(18),式(12)中的Qi,j(x;σ)可以表示为

Qi,j((1+ε)x;σ)≈Qi,j(x;σ+δ)

(20)

其中Qi,j(x;σ)关于σ求偏导,可以写成:

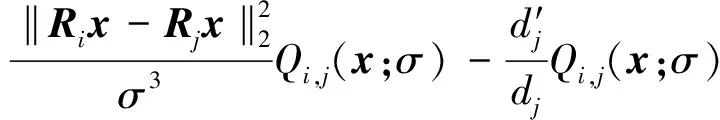
(21)

将式(21)代入到式(20)可得:

(22)

根据式(19),将δ=-εσ代入式(22),可以得到:

(23)

Qi,j(cx;σ)≈Qi,j(x;σ),

(24)

近似满足等式(17).因此,NLM去噪算法满足齐次性条件.

基于字典学习正则化的地震反演方法,先利用测井数据训练更新得到字典,本文采用K-SVD和正交匹配追踪(OMP)迭代的方法,获得的字典记录了地下构造的局部特征,其示意图如图1所示.在通过测井数据x获得字典时,为了提高字典学习的计算效率,并且提供充足的样本,采用滑动窗将测井数据分割成块的形式Rix,利用OMP计算波阻抗Rix在字典P下的稀疏表征Г,然后根据f(Rix)=PΓ恢复出待反演的结果,该步骤相当于线性滤波,满足齐次性条件.因此,对于字典学习算法只需要考虑基于OMP的稀疏表征是否满足齐次性条件,求解该问题可以表示为

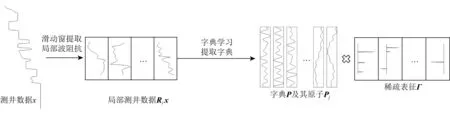
图1 基于测井数据的字典学习示意图Fig.1 Schematic diagram of dictionary learning based on logging data

(25)

其中β2为允许OMP重构稀疏系数与原始波阻抗的偏差.基于OMP的稀疏重构算法如算法2所示.虽然式(25)为非线性问题,但稀疏系数Г可以通过最小二乘法直接求解获得,因此待反演波阻抗的稀疏表征过程满足齐次性条件.

2 合成数据测试

为了证明去噪算法驱动的正则化方法的可靠性和实用性,本文将传统的去噪算法与拉普拉斯正则化结合,分别构造非局部均值滤波和字典学习正则项,并与常规的直接对反演结果迭代滤波的反演方法进行对比.在合成数据测试中,利用合成数据所用子波进行反演,将两种基于去噪算法的正则化方法应用于Marmousi模型的叠后波阻抗反演.在实际资料中,通过井震标定提取的子波作为反演所用地震子波.为了定量表示反演结果的可靠性,采用均方根误差衡量反演结果的精度:

(26)

基于褶积模型,采用主频为30 Hz的雷克子波进行正演模拟,得到无噪叠后观测地震记录,如图2a所示,时间采样间隔为1 ms.在观测记录中加入随机噪声,使其信噪比为2,如图2b所示,以测试所提出方法的抗噪性.图3a、b分别为Marmousi模型的真实波阻抗模型和初始模型,初始模型采用大小为181×181点的平滑窗得到.

图2 模拟的观测地震记录(a) 无噪记录; (b) 信噪比为2的含噪记录.Fig.2 The synthesized observed seismic record(a) Thenoise-free data; (b) The noisy data with SNR=2.

图3 真实模型和初始模型(a) 真实波阻抗模型; (b) 初始波阻抗模型.Fig.3 The true and initial models(a) The true acoustic impedance model; (b) The initial acoustic impedance model.

为了便于对比,本文将非局部均值滤波和字典学习算法引入到模型约束的迭代反演中,得到的反演结果如图4a和图5a所示.在迭代反演过程中,先通过模型约束得到初始反演结果,再对初步反演结果进行滤波,得到的结果作为新的参考模型进一步约束反演(She et al., 2018, 2019; Dai et al., 2019).分别将两种去噪算法结合到拉普拉斯正则化中,得到的反演结果如图4b和图5b所示.理论上,迭代滤波反演没有考虑反演结果正演合成记录与观测记录的匹配问题.基于非局部均值滤波的方法,虽然可以有效消除反演结果中的小扰动,但是模糊了边界等有用信息.而基于字典学习的迭代反演方法,虽然可以有效提取研究工区的局部构造,但字典学习是在单道上进行处理的,没有充分利用观测地震记录的空间信息,因此横向连续性较差,信噪比较低.相比之下,去噪算法驱动的正则化方法的反演结果,在保证高信噪比的同时,有效保护了边界和断层等信息.为了定量对比去噪算法驱动的正则化方法的反演效果,分别计算四种方法反演结果的均方根误差,如表1所示.相比于传统模型约束的迭代滤波反演策略,基于去噪算法的正则化方法反演结果精度更高.

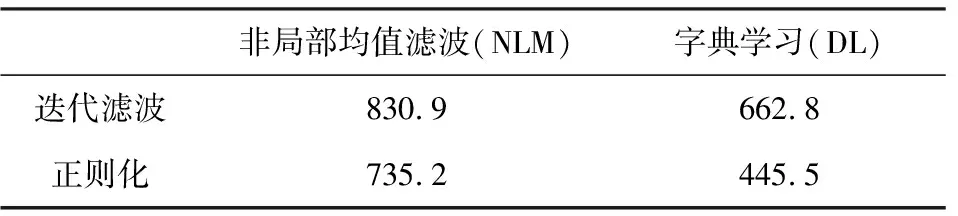
表1 反演结果均方根误差Table 1 Root-mean-square error of inversion results

图4 基于非局部均值滤波的反演结果(a) 常规迭代滤波的反演结果; (b) 基于去噪算法正则化的反演结果.Fig.4 The inversion results by NLM filter(a) The conventional inversion result by iterative filtering; (b) The inversion result by denoising algorithm driven regularization.

图5 基于字典学习的反演结果(a) 常规迭代滤波的反演结果; (b) 基于去噪算法正则化的反演结果.Fig.5 The inversion results by DL(a) The conventional inversion result by iterative filtering; (b) The inversion result by denoising driven regularization.

为了进一步验证所提出正则化方法的反演效果,计算各个采样点和CDP的反演结果与真实模型的相关系数,如图6所示.图6a、b为基于NLM滤波算法的迭代滤波(NLM-Filt)和正则化方法(NLM-REG)的反演结果与真实模型的相关系数,图6c、d为基于DL去噪算法的迭代滤波(DL-Filt)和正则化方法(DL-REG)的反演结果与真实模型的相关系数.可以观察到,无论在不同CDP上还是采样点上,对于相同的去噪算法,基于去噪算法正则化的反演结果精度高于迭代滤波方法.为了验证超参数λ对反演结果的影响,分别在非局部均值滤波正则化和字典学习正则化反演中测试不同λ的影响,如图7a所示.超参数λ的选取决定了反演效果,当λ过大时,使反演结果呈现出去噪算法期望的特征,却难以准确匹配观测记录,而λ过小时,会使反演结果更匹配含噪的观测记录,出现较大误差.在模型测试和实际数据测试中,本文利用已知井数据确定λ的取值.此外,分别在不同信噪比的观测资料下,本文测试了反演结果对观测记录噪声的敏感性,不同信噪比观测地震记录的反演结果的RMSE如图7b所示.去噪算法驱动的正则化方法不容易受到观测记录中噪声的影响.为了检验去噪算法正则化反演方法的收敛性,分别记录了两种去噪算法正则化的目标函数值和反演结果的均方根误差随迭代次数的变化,示于图8和图9.可以看到,在反演过程中,目标函数值和反演结果的均方根误差逐渐减小,最终收敛到稳定的值.

图6 各采样点和CDP反演结果与真实模型的相关系数变化 基于NLM去噪算法的(a)不同CDP和(b)不同采样点的相关系数变化; 基于DL去噪算法的(c)不同CDP和(d)不同采样点的相关系数变化.Fig.6 Correlation coefficients variation with sampling points and CDPs Correlation coefficients of inversion results by NLM (a) at different CDPs and (b) at different sampling points, DL (c) at different CDPs and (d) at different sampling points.

图7 反演结果均方根误差随(a)超参数λ的变化和(b)信噪比的变化Fig.7 RMSE variation with (a) hyper-parameter λ and (b) SNR

图8 基于非局部均值滤波正则化的(a)均方根误差和(b)目标函数值随迭代次数的变化Fig.8 (a) RMSEand (b) objective function variation with iterations of NLM regularization

图9 基于字典学习正则化的(a)均方根误差和(b)目标函数值随迭代次数的变化Fig.9 (a) RMSE and (b) objective function variation with iterations of DL regularization

3 实际数据测试

为了验证去噪算法驱动的地震反演正则化策略在实际应用中的效果,选择OpendTects开源工区F3反演数据集中纵测线Inline=244过井(F06-1)剖面进行叠后波阻抗反演.该工区地震记录的时间采样间隔为4 ms,通过井震标定提取用于反演的地震子波.二维地震记录剖面如图10a所示,利用该工区测井数据和层位信息,通过低通滤波和内插外推得到波阻抗初始模型,如图10b所示.可以看到该地震剖面浅层信噪比较低,横向连续性较差.本文分别测试非局部均值滤波正则化和字典学习正则化的反演效果,并与传统的迭代滤波类方法进行对比.

图10 (a) 叠后地震记录; (b) 波阻抗初始模型Fig.10 (a) The poststack seismic data; (b) Initial acoustic impedance model

图11a、b分别为非局部均值滤波和正则化的反演结果.图11a突出了低频的构造信息,却严重降低了反演结果的分辨率.图11b有效提高了反演结果的空间连续性和分辨率.字典学习迭代滤波算法反演结果(图12a)由于是在单道上进行的,往往表现出较差的空间连续性和较低的信噪比,而基于字典学习正则化的反演结果(图12b)信噪比和分辨率相对更高.通过与位于CDP 88处的测井曲线(图13)对比可以看到,反演结果与测井曲线匹配较好,存在的偏差主要由井震频带不匹配和井震标定偏差造成.分别计算四种方法的反演结果与测井曲线的均方根误差,如表2所示,可见,引入去噪算法正则化的反演结果与传统迭代滤波方法相比精度较高,在剖面中有效提高了反演结果的空间连续性和分辨率.

表2 反演结果均方根误差Table 2 Root-mean-square error of inversion results

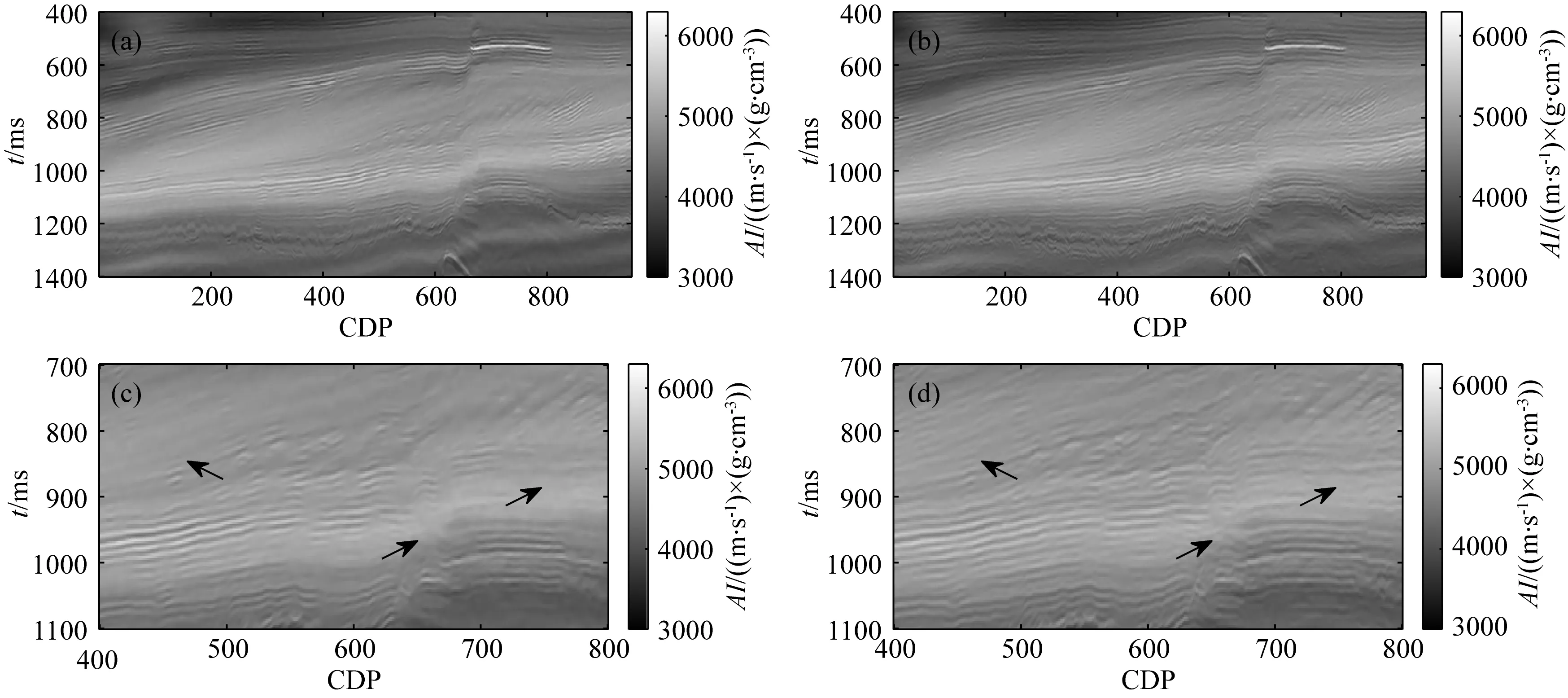
图11 (a) 基于非局部均值滤波的反演结果; (b) 基于非局部均值滤波正则化的反演结果; (c) 局部放大的基于非局部 均值滤波的反演结果; (d) 局部放大的非局部均值滤波正则化的反演结果Fig.11 The inversion results by (a) NLM filter and (b) NLM regularization; The local zoomed in results from (c) NLM filter inversion result and (d) NLM regularized inversion result

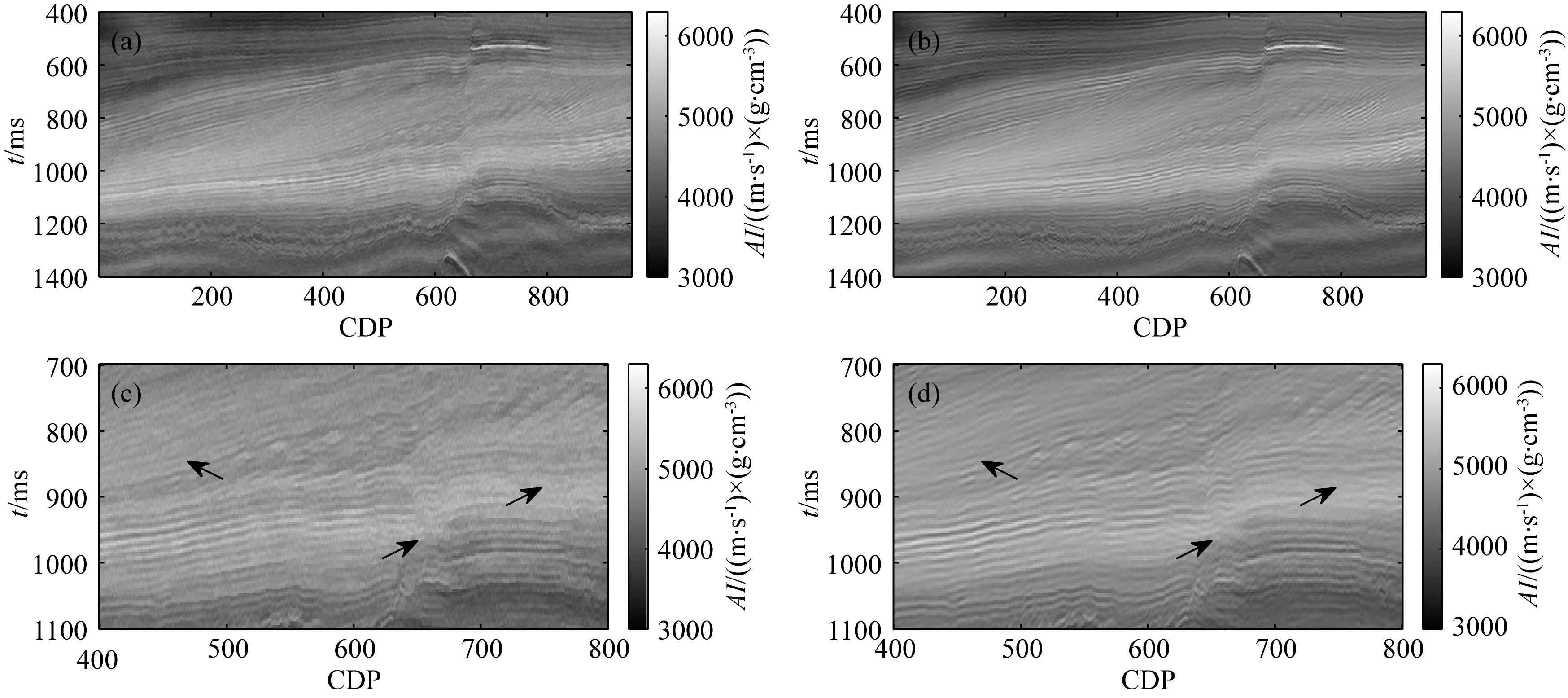
图12 (a) 基于字典学习滤波的反演结果; (b) 基于字典学习正则化的反演结果; (c) 局部放大的基于字典 学习滤波的反演结果; (d) 局部放大的字典学习正则化的反演结果Fig.12 The inversion results by (a) DL filter and (b) DL regularization; The local zoomed in results from (c) DL filter inversion result and (d) DL regularized inversion result

图13 反演结果与测井曲线对比(a) 非局部均值滤波正则化反演; (b) 字典学习正则化反演.Fig.13 The comparison between borehole data and inversion results(a) NLM regularization inversion;(b) DL regularization inversion.

4 讨论

本文提出了一种如式(3)所示的去噪算法驱动的正则化方法,虽然成功推导出其对应的导数形式,可进行最优化求解.但从该式形式上看,该式起到的约束作用并不直观.可以考虑其替代形式:

(27)

即期望反演结果同时满足观测地震记录和去噪算法作用后的结果f(x).将该形式展开可以得到:

(28)

可以看到,替代形式的第一项等价于本文提出的正则化策略.但是,这种替代的导数形式会更加复杂,而且需要更多的近似条件才能直接写出其对应的导数形式,因此会带来更多误差.

5 结论

本文提出了一种去噪算法驱动的地震反演正则化策略,利用相对成熟的去噪算法,构建正则项,用于约束地震反演结果.通过构建一种通用的正则化形式,只需要简单地引入去噪算法,就可以构建相应的反演目标函数并得到其梯度.本文首先推导了去噪算法正则化目标函数的导数,并证明了传统的非局部均值滤波和字典学习去噪算法满足齐次性条件,可以直接求导.在模型测试中,分别测试了两种滤波类算法迭代反演和正则化反演.反演结果表明,基于去噪算法正则化的反演结果稳定性和可靠性更高,随着迭代的进行,目标函数逐渐收敛到稳定的值,并且新提出的正则化策略可以采用传统的共轭梯度法有效求解.实际资料测试也表明,基于去噪算法的正则化方法可以有效均衡反演结果的精度和空间连续性.

但是,本文只证明了非局部均值滤波和字典学习去噪算法满足齐次性条件,将其结合到去噪算法驱动的正则化方法中,并在合成数据和实际数据反演中进行了验证,后续可以进一步将更复杂、有效的去噪算法(如卷积神经网络去噪方法)引入到本文所提出的正则化框架中,进一步提高去噪算法驱动的正则化方法的适用范围.