坠物冲击下基于混合代理模型的水下管汇动力学分析方法

2023-11-04任涛郭喜庆曾威陈旭鹏

科学技术与工程 2023年29期

任涛, 郭喜庆, 曾威, 陈旭鹏

(西安石油大学机械工程学院, 西安 710065)

水下管汇具有油气汇集、电力分配和水下控制等功能,是水下油气生产系统的重要节点,其工作性能直接影响海上油气开采的稳定性和安全性。但是,水下管汇在服役过程中受到来自渔船、平台作业船只坠物冲击影响,威胁水下油气生产安全。因此,准确分析坠物冲击下水下管汇主结构的动力学性能,为水下管汇结构设计提供可靠依据,是提升水下管汇防护能力、保护其工作稳定性的有效途径。为了研究海上坠物对水下管汇的影响程度,相关学者通过建立水下管汇有限元模型进行了静力学和动力学分析。例如,余峙伟等[1]为了加快海上坠物对其主结构的碰撞有限元求解过程,采用简化水下管汇主结构模型的方法,提高了撞击载荷下水下管汇主结构的求解速率。娄敏等[2]利用全积分壳单元算法建立管道理论模型,对坠物与水下管道发生的碰撞过程进行了分析研究。鲁中岐等[3]在解决海底管道的腐蚀问题时,采用代理模型方法代替大量仿真试验进行分析研究。孙宝等[4]将代理模型技术引入黏弹性缓冲系统参数优化中,减小了计算复杂度并提高了优化结果。上述研究改善了坠物冲击下水下管汇主结构碰撞的动力学性能,但考虑其原比例模型大和结构复杂的问题,分析过程中均采用了降低尺寸比例和简化模型等方法,一定程度上影响了分析结果准确度[5]。同时,冲击载荷下相关结构的动力学分析属于典型的强非线性问题,当理论模型结构尺寸大且足够复杂时,单次模拟的时间成本特别大,这限制了传统的有限元方法在水下管汇动力学分析中的应用[6]。然而在解决高复杂性工程问题时,往往会导致有限元方法计算量大以及耗时较长,基于此引入代理模型技术可以很大程度提高计算效率,降低时间成本。

基于此,现针对上述采用简化模型和缩小比例等方法导致水下管汇动力学分析精度受损、分析结果不准确的问题,建立水下管汇的全尺寸结构有限元模型进行动力学分析,并针对由此造成计算成本过高的问题,引入代理模型方法提高水下管汇动力学分析效率。进一步地,在代理模型建模过程中,考虑单一代理模型拟合性能的局限性,基于组合预测理论构建水下管汇动力学响应混合代理模型,开展基于混合代理模型的水下管汇动力学分析,在保证分析精度的同时进一步提高其优化效率。

1 单一代理模型基本理论

1.1 Kriging模型

Kriging(KG)代理模型[7]是一种根据变异函数理论构建的插值模型。其在满足插值方差最小的条件下,给出最优线性无偏插值,是一种估计方差最小化的无偏估计模型。其函数模型表达式为

(1)

F(β,x)=β1f1(x)+β2f2(x)+…+βpfp(x)

=fT(x)β

(2)

式中:β为线性回归系数;f(x)为x变量的多项式函数;z(x)为一个随机过程。由于其建模过程较复杂,具体建模过程见参考文献[7]。

1.2 RBF模型

径向基函数(radical basis function,RBF)代理模型[8]是一种利用离散多远数据拟合未知非线性函数的技术。它的基函数是典型径向函数,将径向堆成基函数的自变量设为已知样本点和未知待测点之间的Euclidean距离,径向函数组合得到其模型,也可称为一系列关于样本点的基函数线性和,即为径向基函数模型。其函数模型表达式为

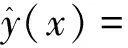
(3)

式(3)中:‖·‖表示欧式距离;Ψ=ψ(‖x-x(i)‖)为基函数;wi为i个样本点的权系数。

1.3 支持向量回归

支持向量回归(support vector regression,SVR)代理模型[9]是一种与支持向量机(support vector machine,SVM)相同原理的监督学习算法。与之不同的是支持向量回归是使用核、稀疏解和VC控制边距和支持向量的数量,它的主要优点是其计算复杂度不依赖于输入空间的维度。此外,具有出色的泛化能力,具有很高的预测精度。其函数模型形式为

(4)

式(4)中:μ为一个给定常量;ωi为i个样本点的权系数;φ为样本集的基本函数。

2 水下管汇主结构碰撞有限元模型

水下管汇主结构不但能够为各类型生产管道和阀门组件提供支撑平台,而且还能够防止海上坠物冲击造成的损伤。在受到坠物撞击时,管汇主结构的基础框架通过变形来承受坠物产生的动载荷。因此,选择水下管汇主结构作为分析对象,并通过适当简化,建立水下管汇结构模型,如图1(a)所示。为降低全尺寸模型的计算成本,并考虑水下管汇主结构的受力特征,在有限元软件中分别使用梁单元和壳单元对管汇主结构中的H型钢和圆柱支撑柱进行有限元划分;坠物和防护板则采用实体单元进行模拟,并定义管汇防护板材料为A36,其他结构材料为Q235。由于防护板是承受坠物冲击的实际结构,因此在划分网格时对防护板的有限元网格进行了适当加密。最终,有限元模型如图1(b)所示。

图1 水下管汇主结构实体模型和有限元模型Fig.1 Solid model and finite element model of main structure of subsea manifold

海上坠物坠落过程中,在受到海水阻力作用下,其经过一定的坠落高度后会呈现一种固定的速度和姿态与防护板进行接触。因此,在碰撞分析过程中认为坠物从管汇正上方坠落且呈固定的速度和姿态。其中,根据DNV规范,坠物的坠落速度采用式(5)进行计算[10],即

(5)

式(5)中:m为坠物的质量,kg;V为坠物的体积(排出水的体积),m3;ρw为水的密度;g为重力加速度,取值9.81 g/m2;CD为阻力系数;A为坠物在流向上的投影面积,m2;vT为坠物的速度,m/s。

海上坠物通常是海上作业渔船、平台等上的落物,根据船舶航运标准规范,主要包括船锚、球形和管型等坠物,因此分别采用圆管、霍尔锚和球体分别模拟3种坠物类型模拟。同时,考虑圆管结构坠落姿态包括纵向和横向两种情况,因此分别模拟圆管(纵向)、圆管(横向)、霍尔锚和球体4种坠物冲击下管汇的动力学响应[11]。如图2所示,为圆管、霍尔锚和球体质量分别是700、1 000、2 000 kg时,4种坠物冲击下管汇主结构的应力云图。

图2 不同海上坠物撞击管汇主结构应力云图Fig.2 Stress nephogram of main structure of manifold impacted by different marine falling objects

图2为圆管纵向、圆管横向、霍尔锚、球体4种坠物与管汇撞击过程最大等效应力时刻,最大等效应力分别为148.14、162.8、201.32、312.75 MPa。由以上数据可知,当4种坠物作为研究对象时,坠物质量越大,碰撞产生的应力越大。由圆管坠物的仿真结果可知,在坠物质量相同的条件下,坠物与管汇碰撞接触面积越小产生的应力越大。该分析在CPU为i7 G4560处理器、64位操作系统以及8 G运行内存的平台上完成,单次有限元动力学分析耗时约48 h。

3 水下管汇动力学指标代理模型建模与预测分析

3.1 代理模型设计变量与响应量

选取坠物霍尔锚、圆管、球体的质量为代理模型的设计变量。由设计要求可知,设计变量的取值范围为初始值上、下波动的1/2,表1为其具体取值区间。

表1 代理模型设计变量区间Table 1 Value ranges of the surrogate model variables

根据水下管汇动力学分析目的,选取坠物与水下管汇碰撞的最大应力值σ、最大应变值ε、能量吸收e以及管汇连接器所在位置的最大加速度a为动力学响应量,构建水下管汇碰撞动力学响应代理模型。

3.2 水下管汇动力学响应KG模型

为保证KG代理模型预测精度,对于高计算成本的管汇结构动力学响应分析,需要选择数量至少为2k的训练样本[12],即

k=(n+1)(n+2)/2

(6)

式(6)中:n为KG模型的设计变量数目。

由于设计变量数为1,因此至少需要的训练样本数为6。为保证样本均匀性,抽样过程中采用拉丁超立方试验设计方法在表1所示区间中进行抽样,并采用构建的水下管汇主结构碰撞有限元模型计算对应的动力学响应指标,得到代理模型训练样本如表2所示。

表2 代理模型训练样本Table 2 Training sample of the surrogate model

采用最大似然估计方法,分别计算圆管(纵向)、圆管(横向)、霍尔锚、球体撞击下水下管汇动力学响应指标KG模型的相关参数,利用式(1)即可构建得到不同动力学指标响应KG模型。

3.3 水下管汇动力学响应RBF模型

以表2中数据为RBF模型的训练样本,以Gaussian函数φ(r,c) = exp(-r2/c2)为基函数。在此基础上,使用Gaussian函数φ(r,c)构建100×100的矩阵φ,并采用公式ω=y′/φ计算得到预测响应值的权系数ω,其中为y′为训练样本中的水下管汇动力学响应指标值,即y′=[y1,y2,…,y100]。最终,坠物冲击下水下管汇的动力学响应RBF模型为

(7)

式(7)中:xn为待预测点。

3.4 水下管汇动力学响应SVR模型

首先定义一个输入值xi和输出值yi的回归函数f(x),选取表2中数据为SVR模型的训练样本集,并将样本坐标引入松弛变量ζi*和ζi,以确定样本的偏离约束程度,其表达式为

(8)

然后引入Largrange函数乘子α,有

(9)

根据式(9)计算得到最优解α={α1,α2,…,

αn},进而得到水下管汇动力学响应指标的权重参数和偏置量。最终,坠物冲击下水下管汇的动力学响应SVR模型为

(10)

式(10)中:α和α*为对偶变量;K(xi,xj)为核函数。

分别使用构建的RBF、KG、SVR3种代理模型对海上坠物撞击水下管汇主结构的应力值、应变值、连接器处的加速度、能量吸收进行预测,结果如图3所示。

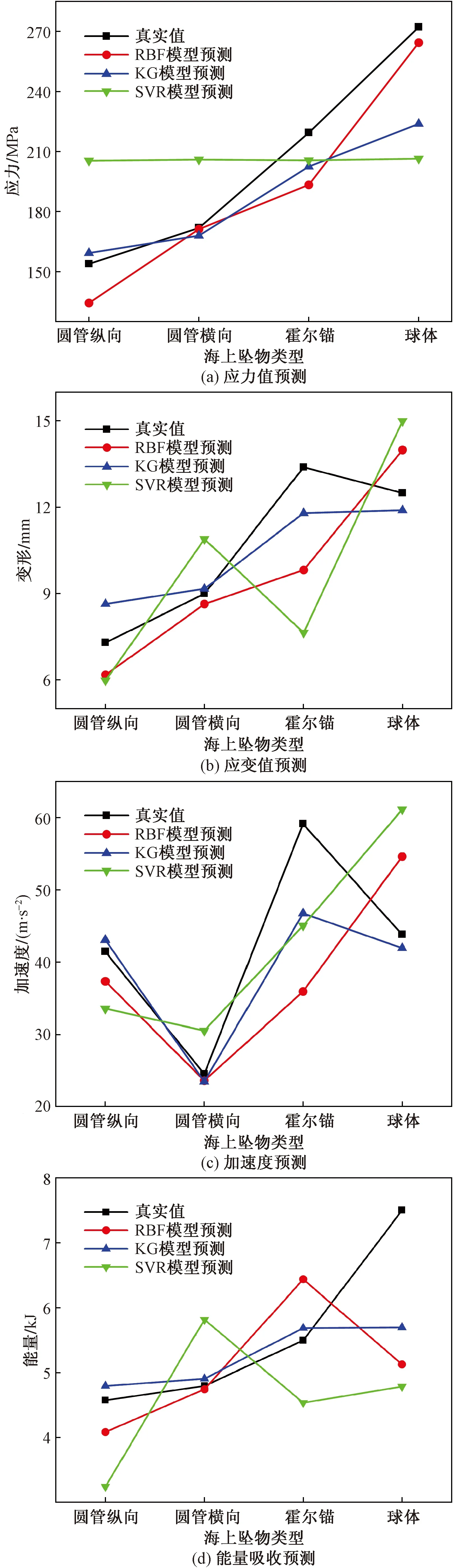
图3 不同单一代理模型预测结果Fig.3 Forecast results of different single surrogate models

3.5 3种代理模型精度分析

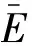
(11)

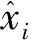
表3 单一代理模型误差对比Table 3 Error comparisons of single surrogate model

根据表3误差对比结果,与RBF和KG模型相比,SVR模型预测值对于应力值、应变值、加速度、能量吸收的平均误差最大,分别为20.95%、25.47%、26.71%、25.97%,这表明RBF和KG模型对于坠物冲击下管汇动力学响应指标的预测更加准确。

4 基于混合代理模型的水下管汇动力学分析

4.1 水下管汇动力学响应混合代理模型建模

混合代理模型是将两种及以上的单一代理模型组合起来,构建一个有更高精度的预测模型,且其计算精度一般高于单一的代理模型[13],其基本思想是充分利用单一代理模型的预测能力,使混合代理模型拥有多个单一代理模型的预测高精度性。混合代理模型的结构一般可以描述为

(12)

式(12)中:yE(x)为混合代理模型在预测点x处的预测值;Ns为单个代理模型的个数;wi为对应代理模型的权重值;yi(x)为第i个代理模型在预测点x处的预测值。

由式(12)可知,权重比例直接决定了单一代理模型预测值的占比大小。根据模型混合理念,单一代理模型预测精度越高,其在混合代理模型中所占权重比越大,反之,预测精度越低,在混合代理模型中占比越小。因此,当权重比例合适时,混合代理模型的预测精度可以达到最大化。为提高代理模型的预测精度,采用混合代理模型对不同海上坠物与水下管汇的碰撞动力学响应结果进行预测。根据表3中代理模型的预测误差对比结果,选择预测精度更高的RBF和KG模型作为混合代理模型的子模型[14],并采用平均加权法进行组合。混合代理模型表达式为

Y(x)=ω1φ1(x)+ω2φ2(x)

(13)

式(13)中:x为自变量;φ1为径向基代理模型;φ2为克里金代理模型;ω1和ω2分别为两个模型的权重系数。

子模型的权重系数直接影响着混合代理模型预测值的精度[15],为保证模型精度,采用克拉默法则进行权重计算,其具体计算公式如下。

(14)

AΩ=β

(15)

式中:A=[aij]n×n,Ω=(ωi1,ωi2,…,ωin)T,β=(b1,b2,…,bn)T,A为各代理模型预测值系数矩阵,Ω为由权重系数组成的列向量,β为由真实值组成的列向量。

计算过程中,根据两个代理模型在同一个已知点的预测值,分别给予一个未知系数,联合该点的真实值得到权重系数的方程组。将每个点逐个测验,最终计算出每组的权重系数,混合代理模型权重系数如表4所示。

表4 混合代理模型权重Table 4 Weights of the hybrid surrogate model

基于表4中混合代理模型子模型权系数计算结果,可以构建得到不同动力学响应指标对应的混合代理模型,其基本形式为

(16)

4.2 混合代理模型预测精度

为检验混合代理模型的预测精度,将混合代理模型预测结果分别与RBF、KG代理模型和真实值进行对比,结果如图4所示。进一步地,采用式(11)所示平均相对误差为评价指标计算各代理模型的预测误差,具体结果如表5所示。

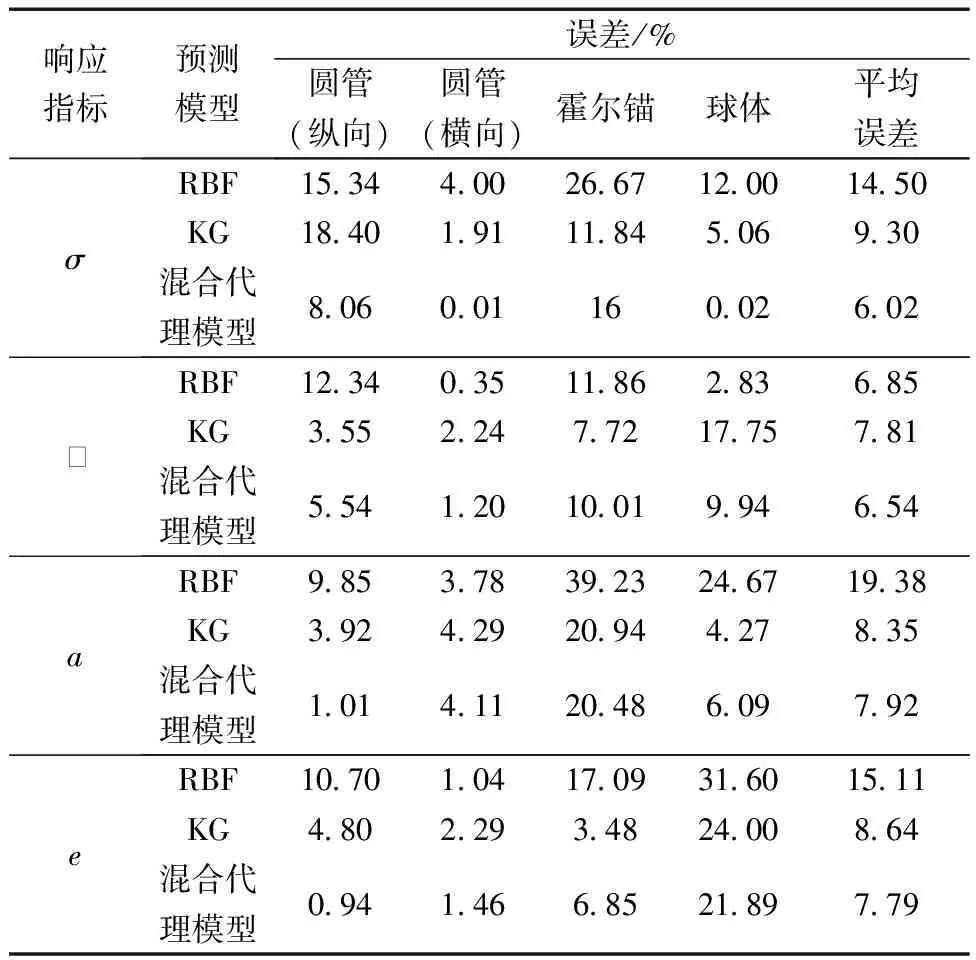
表5 动力学响应指标代理模型预测误差Table 5 Prediction errors of the surrogate models for dynamic responses

图4 混合代理模型预测值对比Fig.4 Comparison of predicted values of hybrid surrogate model

由图4可以看出,混合代理模型相比于单一代理模型的预测曲线更接近于真实值曲线。根据表5结果可知,对于坠物冲击下水下管汇主结构应力值、加速度和能量吸收预测,RBF预测精度最低,平均相对误差分别为14.5%、19.38%和15.11%;KG模型预测精度次之,平均相对误差分别为9.3%、8.35%和8.64%;混合代理模型预测精度最高,平均相对误差分别为6.02%、7.92%和7.79%。对于应变值预测,KG模型预测精度相对最低,平均相对误差为7.81%;RBF次之,平均相对误差为6.85%;混合代理模型预测精度最高,平均相对误差为6.54%。总的来讲,对于坠物冲击下水下管汇主结构应力值、应变值、加速度和能量吸收,混合代理模型均具有最高的预测精度。另外,根据表5还可以计算混合代理模型对应各响应指标的总体平均预测误差为7.07%,根据表3可计算出3种单一代理模型的总体平均误差为17.19%。这表明相比单一代理模型,混合代理模型平均预测精度提高了10.12%。