精轧螺纹钢混凝土柱抗震性能理论与数值模拟

2023-11-04张香成赵佳宝王治东刘郑勇赵军

科学技术与工程 2023年29期

张香成, 赵佳宝, 王治东, 刘郑勇, 赵军*

(1.郑州大学力学与安全工程学院, 郑州 450001; 2.中建五局河南公司, 郑州 450001)

地震震害调查结果表明[1-2],按照现行规范设计的钢筋混凝土抗震结构在遭遇较大地震作用后会发生较大损伤,导致结构抵抗余震的能力较弱;且震后残余变形较大,导致结构难以修复。崔洪军等[3]对于装配式结构进行调研分析,指出了装配式结构同样存在震后变形较大、修复成本较高的问题。针对上述钢筋混凝土结构的这一缺陷,许多学者将超高强筋材用于混凝土抗震结构中,利用超高强筋材抗拉强度高、线弹性好和黏结强度低的特点形成了具有一定可恢复功能的抗震结构。赵军等[4-6]将钢筋混凝土剪力墙或柱中的部分纵向钢筋替换为碳纤维增强复合材料筋材(carbon fibre-reinforced polymer,CFRP)并开展了一系列的抗震性能试验研究。但是这种纤维增强复合材料筋材的低弹性模量和较低的抗剪抗压强度限制了这种筋材的应用[7]。刘志华等[8]、邵家邦等[9]和Takeuchi等[10]分别对钢绞线混凝土圆柱、低黏结超高强钢筋混凝土圆柱进行了抗震性能试验研究,结果表明:自复位结构在大位移角下具有较小的残余变形,有利于震后结构的修复,但耗能能力相对较差。

随着抗震理论研究的深入及有限元软件的广泛应用,许多学者对混凝土柱弯矩-曲率的计算和恢复力模型进行了研究,取得了丰富的研究成果。Al-Kamal等[11]提出了一种新的混凝土柱受压区应力分布计算方法。解咏平等[12]提出了等效屈服曲率和极限曲率的计算方法,推导出了考虑弯曲变形、剪切变形和黏结滑移变形影响的极限位移计算公式。马颖等[13]提出了确定弯剪破坏柱开裂、屈服和破坏时对应荷载及位移的计算方法,并提出了弯剪破坏柱恢复力模型骨架曲线的简化方法。

与前人采用的低黏结高强度筋材不同,精轧螺纹钢(prestressing-screw bars,PSB)又名预应力混凝土用螺纹钢筋,与混凝土之间的黏结强度更好,理论上能够极大地提高试件的水平承载力,保障地震中人民的生命安全,同时增强结构的耗能能力,克服自复位结构耗能能力相对较差的缺点。为了研究PSB筋材混凝土柱的抗震性能,现采用MATLAB软件基于截面分割法理论开发一种PSB筋材混凝土柱抗震性能的计算程序,提出一种框架柱抗震性能的计算方法,对PSB筋材混凝土柱在不同混凝土强度、轴压比和配筋率下的抗震性能进行对比分析。

1 计算方法及模型验证

1.1 混凝土材料的本构及滞回模型

混凝土材料的本构模型采用由Sakino等[14]提出的混凝土模型,骨架曲线如图1所示。

图1 混凝土材料模型骨架曲线Fig.1 Skeleton curve of concrete material model

该混凝土模型包括约束混凝土和无约束混凝土两种应力-应变关系,关系曲线由式(1)定义。

(1)

式(1)中的相关参数由以下一系列公式计算得到。

(2)

式(2)中:fc为混凝土应力;εc为混凝土应变;f′cc为约束混凝土峰值应力;εc0为约束混凝土峰值应力时对应的应变;f′c为无约束混凝土轴心抗压强度;ε0为无约束混凝土达到最大应力时的应变,50 MPa级别混凝土取ε0=0.002 0,f′c=50 MPa;K为约束混凝土强度增大系数,取K=1.1。

混凝土模型的卸载与再加载规则采用Sun等[15]提出的混凝土滞回规则。如图2所示。

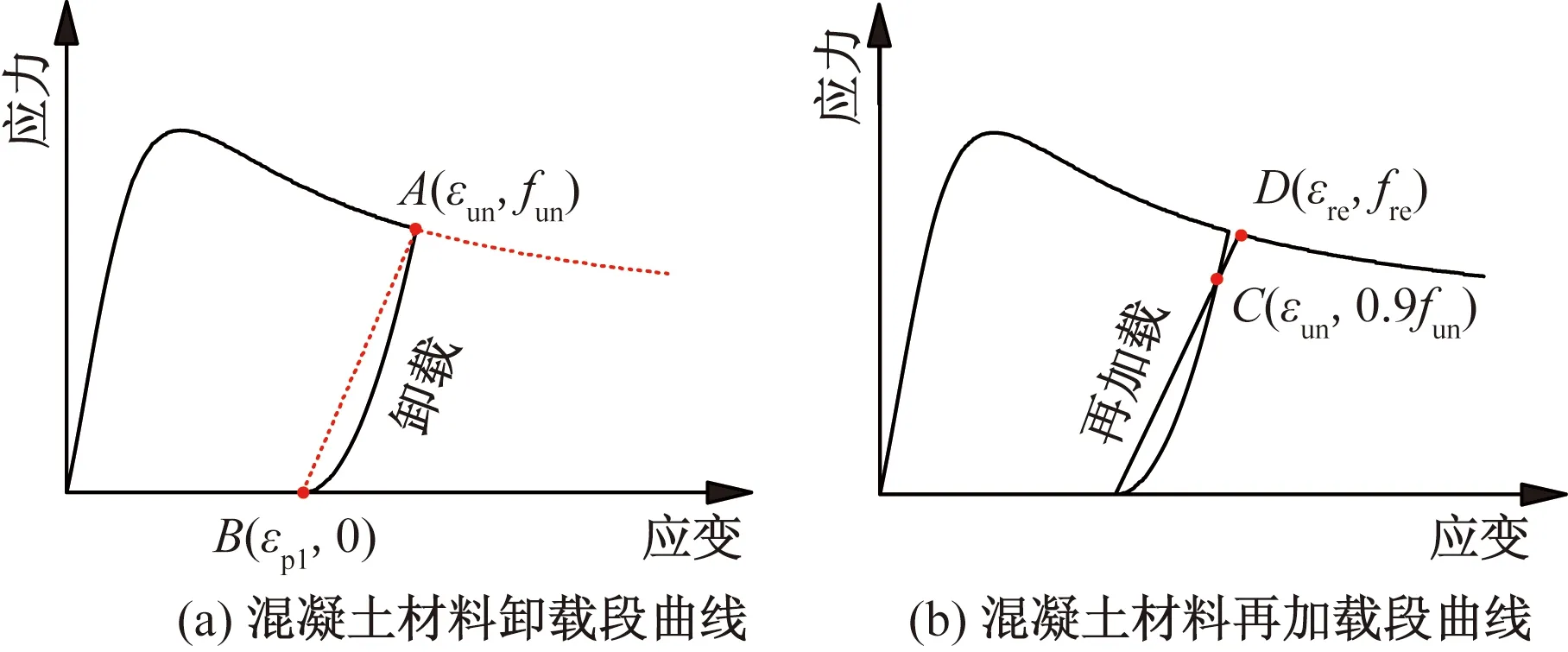
图2 混凝土材料滞回规则Fig.2 Hysteresis rules of concrete materials

当A(εun,fun)点为卸载起始点时,将卸载曲线定义为一条以B(εpl,0)点为顶点的二次曲线。卸载阶段曲线方程如式(3)所示,其中B点定义为:以混凝土弹性模量Ec为斜率且过A点的直线与横坐标轴的交点,B点横坐标可由式(4)计算得到。

该混凝土本构不考虑混凝土的受拉性能,卸载到混凝土应变小于εpl后应力为0。当卸载结束重新加载时,再加载路线是一条经过B(εpl,0)点和C(εun,0.9fun)点的直线。假定该直线与混凝土骨架曲线相交于D(εre,fre)点,当再加载混凝土应变值超过D点横坐标之后时,仍沿着最初的混凝土骨架曲线进行计算,再加载时应力应变方程如式(5)所示。

(3)

(4)

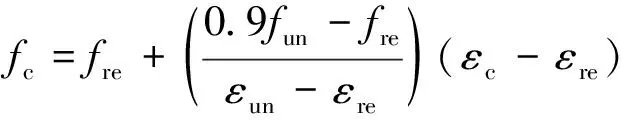
(5)

1.2 PSB筋材的本构及滞回模型

钢筋的本构曲线如图3所示。曲线由通过渐近线相连接的两条直线和由弹性段向完全塑性段过度的弹塑性段曲线组成。骨架曲线的初始切线刚度为Es,峰值点处的切线刚度为Et=QEs,骨架曲线方程如式(6)所示[16],参数Q与εch的计算公式如式(7)所示。

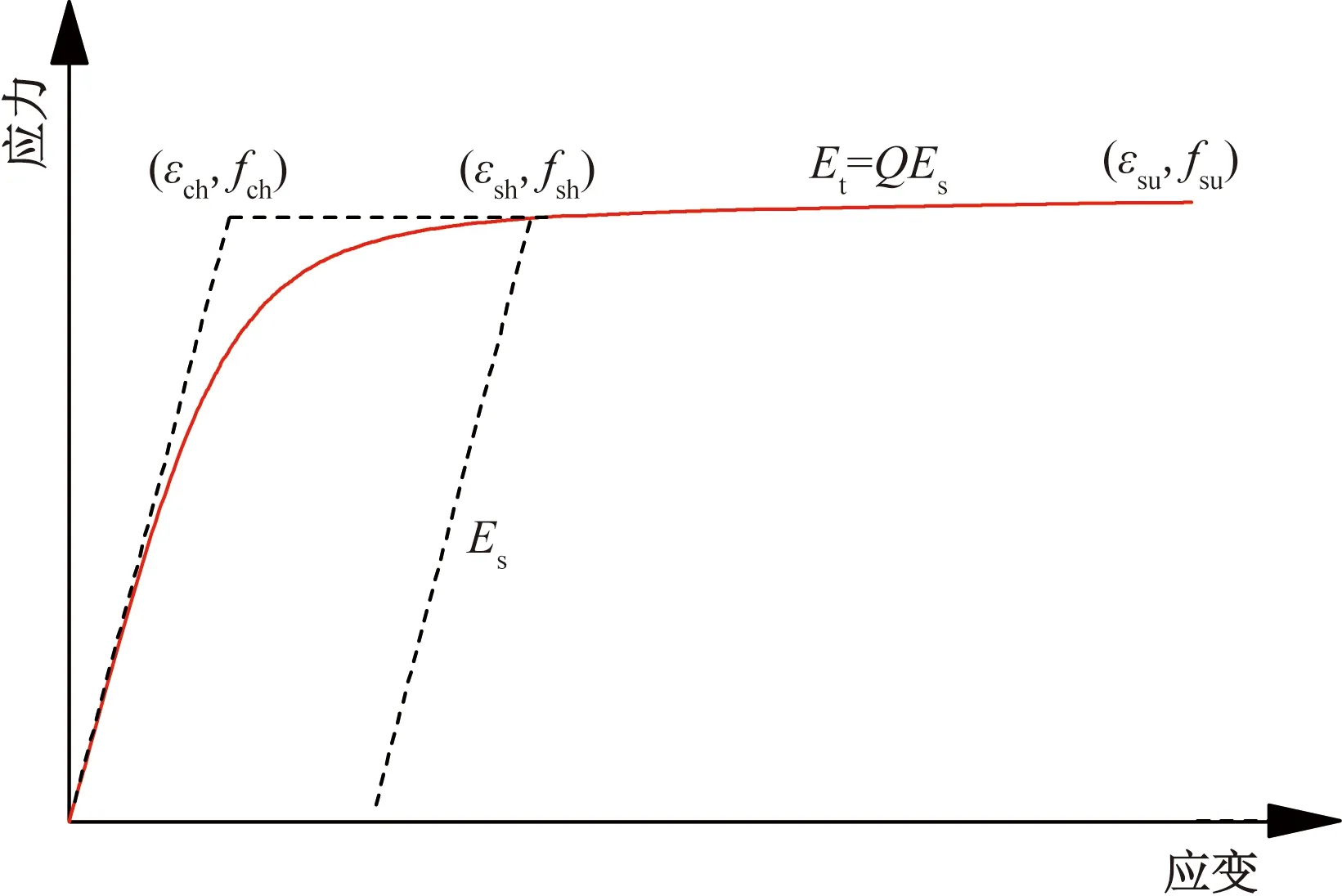
图3 钢筋材料骨架曲线Fig.3 Skeleton curve of reinforced material

(6)

(7)

式中:fs和εs分别为PSB筋材的应力和应变;Es为PSB筋材的弹性模量;εch为特征应变值;Q为峰值点处切线刚度与初始切线刚度的比值;C为连接两条直线的渐近线的曲率系数,取3.0。

该筋材模型的滞回规则如图4所示,3种工况分别如下。

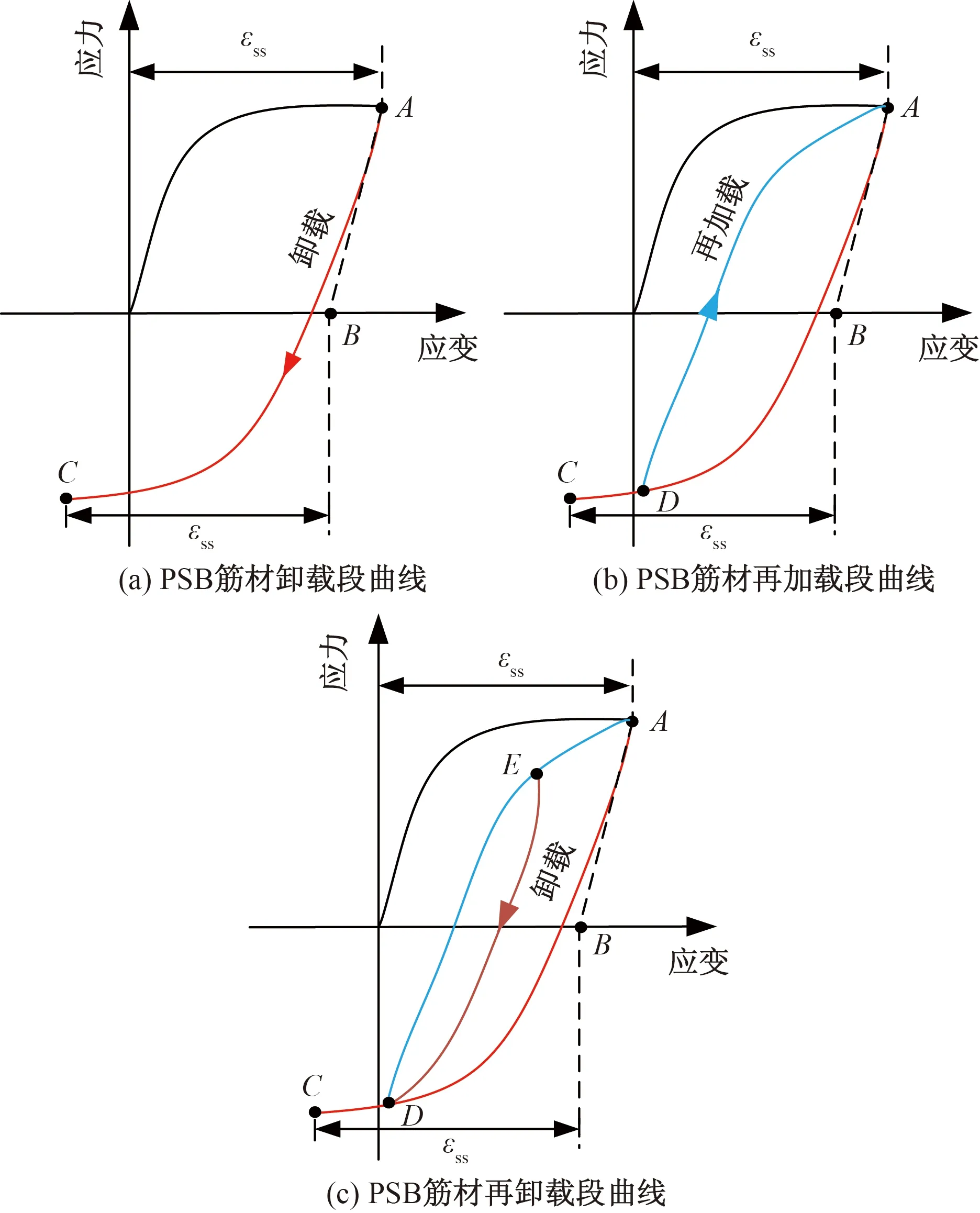
图4 钢筋材料滞回规则Fig.4 Hysteresis rules of steel bar materials

(1)当从骨架曲线上的A点开始卸载或者反向加载时,认为反向加载应力应变曲线的结束点是以点B(εmo,0)为原点的反向骨架曲线的与A点相对应的点C(εb,fb),C点相对于B点的相对应变等于A点的应变值。

(2)当从A点卸载沿图4(a)中所述曲线达到A点和C点之间的D点时,开始正向加载,将点A定义为再加载曲线的结束点,D点为起始点。

(3)当从D点正向加载后,在还没有到达A点之前的E点再次卸载,则认为E点为再卸载曲线起始点,上次再加载的起始点D点为结束点。

起始点和结束点确定后,仍使用Menegotto-Pinto[16]方程来定义卸载和再加载曲线,应力应变关系方程如式(8)所示。

(8)

式(8)中:Q1为结束点处的切线斜率与起始点处切线斜率的比值,起始点处的切线斜率即为Es。为了保证卸载和再加载后,曲线经过上次循环的结束点时应变连续,假定第一次加载曲线和再加载曲线在A点处的切线斜率相等。基于试验结果,Fukuhara等[17]提出了渐近线的弯曲系数C1的计算公式,如式(9)所示。

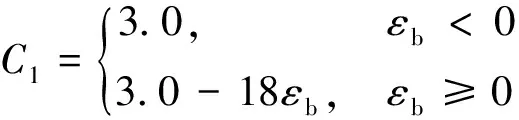
(9)

式(9)中:εb为结束点的应变,当εb为正值时考虑其对C1的影响,当εb为负值时默认C1=3.0。确定C1和Q1后,把结束点坐标代入最初的Menegotto-Pinto方程中,计算出新曲线对应的εch1。

1.3 截面分割法

使用文献[18]中的M-φ截面分割法对低周反复荷载作用下PSB筋材混凝土柱的滞回性能进行计算分析,其中M为截面的弯矩,φ为截面的曲率,该方法基于材料力学相关知识根据结构的截面性质计算结构的受力情况。将构件分为3个部分:锚固区、塑性铰区和弹性区。在每个区域中,柱截面都被划分为有限个单元,混凝土柱分区如图5所示。

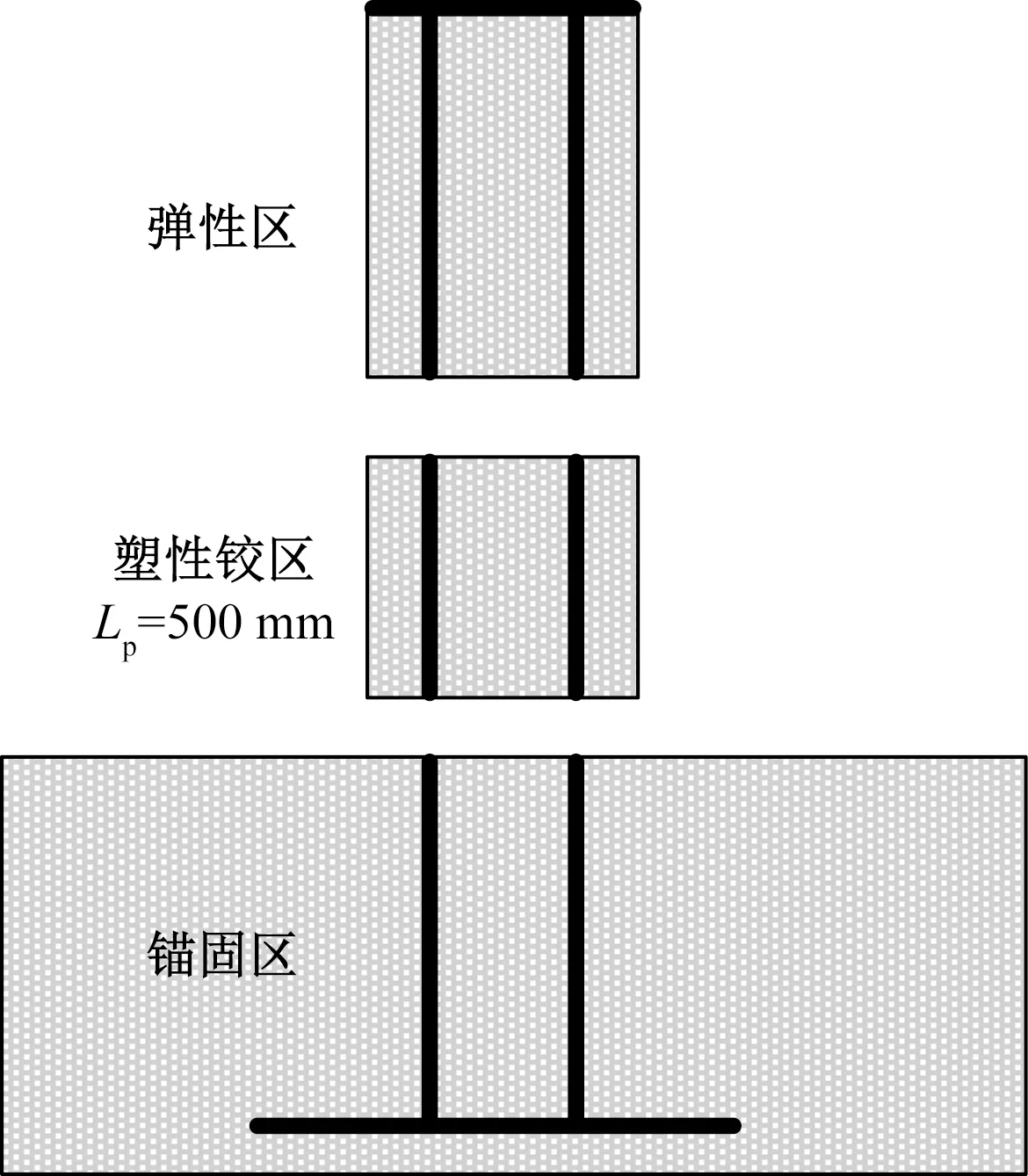
Lp为塑性铰区的高度

使用M-φ截面分割法分析时假定:不考虑混凝土的抗拉强度;混凝土在变形过程中符合平截面假定;混凝土、PSB筋材的本构关系已知;不考虑PSB筋材与混凝土之间的黏结滑移;塑性铰区的高度为1.0D,D为柱截面宽度;在塑性铰区内,PSB筋材的应力和应变均匀分布。

采用M-φ截面分割法分析PSB筋材混凝土柱滞回性能的步骤如下。

步骤1把整个构件划分为3个部分:根部锚固区,塑性铰区,弹性区。

步骤2对于任意一个给定的位移角Rk,计算塑性铰区的平均曲率,计算公式如式(10)所示。

(10)

式(10)中:φk为塑性铰区的平均曲率;L为柱的计算高度。

步骤3由混凝土截面中部纤维的初始应变值εk,可得整个截面混凝土纤维及钢筋纤维的应变分布。计算示意图如图6所示。

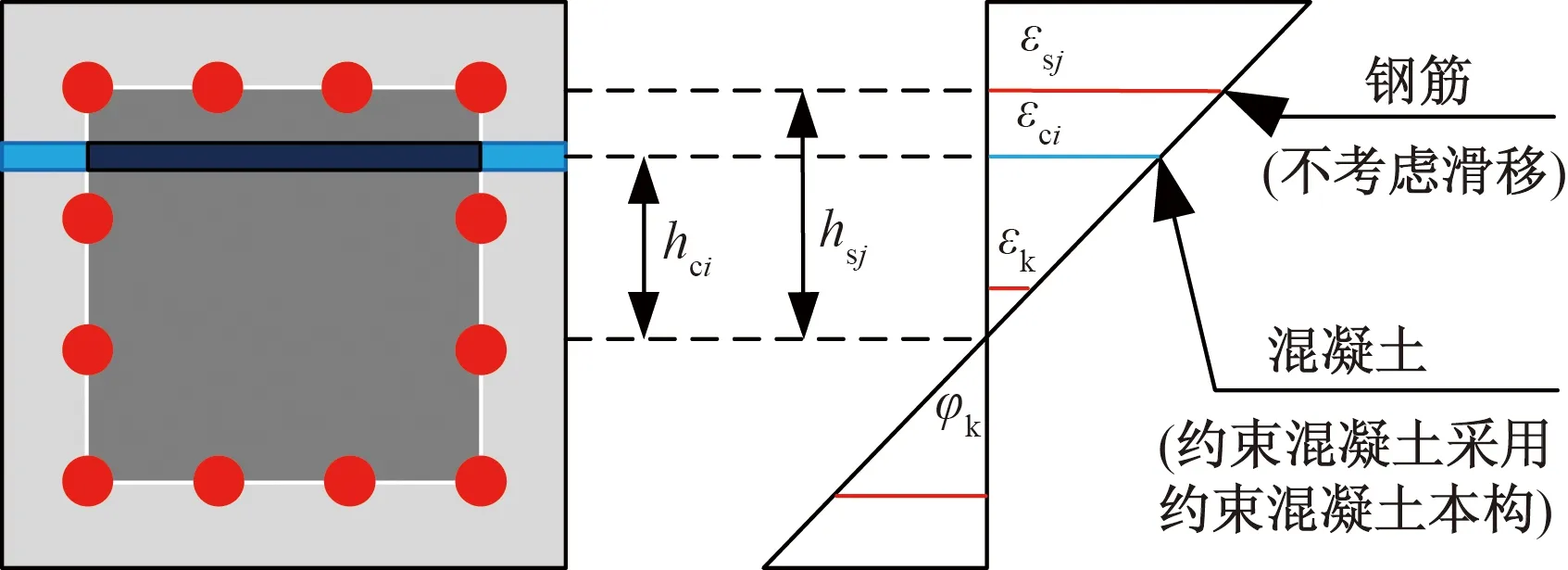
图6 柱截面应变分布Fig.6 Strain distribution of column section

步骤4基于PSB筋材和混凝土的本构关系,可得PSB筋材纵筋和混凝土的应力。

步骤5根据式(11)和式(12)计算塑性铰区混凝土截面应力合力N和弯矩M。

(11)

(12)

式中:nc为混凝土纤维的数量;σci为第i个混凝土纤维应变为εci时的应力;Aci为第i个混凝土纤维的面积;hci为第i个混凝土纤维到截面中性轴的距离;ns为钢筋纤维的数量;σsj为第j个钢筋纤维在应变为εsj时的应力;Asj为第j个混凝土纤维的面积;hsj为第j个钢筋纤维到截面中性轴的距离。

步骤6截面弯矩M即为在位移角Rk作用下的截面弯矩Mk。若塑性铰区构件截面的合力N和轴向荷载P误差较大,则重新假定新的混凝土截面中部纤维的应变εk,重复步骤3～步骤5直到误差满足要求。

步骤7得到真实的构件截面弯矩Mk,侧向荷载Vk=Mk-PRk。

步骤8给定一个新的位移角Rk,重复上述步骤,直到到达指定的位移角。

1.4 MATLAB编程建模及模型验证

1.4.1 MATLAB编程建模

基于MATLAB软件是采用2.3节所述的M-φ截面分割法计算钢筋混凝土柱的滞回曲线。主要步骤如下。

步骤1自动生成位移加载制度,设定每个加载等级的位移角幅值和每个加载等级的循环圈数;设定相邻加载制度之间的误差以及单圈循环的周期。编写好加载制度的循环后输出加载制度示意图以便于检查。

步骤2对PSB筋材混凝土柱计算滞回曲线的理论方法做整体设定,设定相关参数。输入矩形截面相关参数,将矩形截面分割为核心区和非核心区,并对纤维截面面积计算;划分单元,沿PSB筋材混凝土柱截面高度划分单元数量为50,矩形截面分割后单元面积100个,其中1～50为每个单元核心区混凝土的面积,51～100为非核心区混凝土单元面积;设置塑性铰区,输入构件有效高度和塑性铰区域长度;设定混凝土和PSB筋材的滞回模型,考虑箍筋的约束效应,保护层混凝土和核心区混凝土分别按照2.1节中无约束混凝土和约束混凝土模型计算输入相关参数及滞回规则,筋材依据2.2节中模型输入本构及滞回规则。

步骤3设定本计算模型为不考虑PSB筋材与混凝土的黏结滑移。记录每个加载步混凝土单元截面应变和混凝土骨架曲线往复加载历程,记录每个加载步的钢筋截面应变。对混凝土截面单元应力应变及其加载历史赋初值,使用二分法解析,二分法的解的值为0.000 01,收敛误差设为0.000 005。

步骤4设置轴压比,由轴心抗压强度计算柱轴力P,计算滞回曲线。由所有荷载步每个混凝土和钢筋单元的应变和应力,求柱截面纵筋和混凝土的合力N及弯矩M。如果塑性铰区构件截面的合力N和轴向荷载P在误差满足要求且截面受力达到平衡,则截面弯矩M即为在位移角Rk作用下的截面弯矩Mk。即可通过公式计算所有荷载步的水平荷载V。最终检查并输出各模型滞回曲线结果图及计算结果数据。

1.4.2 模型验证

为验证有限元模型参数设置以及材料本构模型的可靠性,对普通钢筋混凝土柱试件SRC-0%-0.15和SRC-0%-0.30(SRC表示全部采用普通钢筋的钢筋混凝土柱,0%表示CFRP筋的替代率为0%,0.15和0.3为试验的轴压比)的试验结果[4]进行验证,依据试验实测值设置混凝土和筋材的相关参数,通过数值计算得到滞回曲线如图7所示。

图7 计算滞回曲线与试验滞回曲线对比Fig.7 Comparison of calculated and experimental hysteresis curves

从图7中可以看出,计算滞回曲线与试验滞回曲线吻合良好,计算和试验的滞回曲线趋势和形状一致。随着轴压比的增大,计算得到的峰值承载力有所提升,峰值承载力对应的位移角有所增大。试件峰值承载力的试验结果与计算结果基本一致,误差很小;试件峰值承载力对应的位移角计算结果比试验结果偏小,误差稍大,这是因为不考虑黏结滑移时会高估模型的侧向刚度[19]。滞回曲线关键点参数对比见表1。通过对比可以判断,该计算模型能考虑PSB筋材筋材替换率、混凝土强度、轴压比对骨架曲线的影响,模型可靠。

表1 滞回曲线特征点数据对比Table 1 Comparisons of characteristic points of hysteresis curves

2 模型设计及加载制度

2.1 模型尺寸

设计了9个混凝土方柱数值仿真模型,模型由柱体和刚性底座两部分组成,在建立模型时柱根部视为固定约束,柱高为1 500 mm,柱体截面尺寸为500 mm×500 mm,剪跨比为3,混凝土保护层厚度为25 mm。纵筋采用直径为16 mm的PSB1080筋材。模型的几何尺寸及配筋情况如图8所示。

图8 模型几何尺寸及配筋图Fig.8 Geometric dimensions and reinforcement diagrams of model components

2.2 模型变量

保持图8中模型几何尺寸不变,改变PSB筋材配筋率、混凝土强度和轴压比,设置3组不同变量的数值模拟组,如表2所示。

表2 试件分组及设计参数Table 2 Grouping of specimens and design parameters

2.3 材料参数

在分析模型中,混凝土和PSB筋材采用的部分参数如表3和表4所示。当f′c=50 MPa时,根据系列公式[式(2)]中的f′cc=Kf′c计算得到f′cc=55 MPa,根据系列公式中的εc0=ε0[1+4.7(K-1)]计算得到εc0=0.002 94,其他参数根据混凝土本构关系设置。PSB筋材的极限拉应变εsu=4%,极限抗拉强度为1 370 MPa,受拉弹性模量Es=201 GPa,其他参数参照式(6)～式(9)计算得到。

表3 混凝土材料参数Table 3 Concrete material parameters

表4 PSB筋材材料参数Table 4 Material parameters of PSB

2.4 加载制度

计算模型的加载制度如图9所示,位移角定义为Δ/L,其中Δ表示模型水平位移,L为模型的有效高度1 500 mm。Rk≤2%时,每个加载等级循环两次;Rk>2%时,每个加载等级循环一次。

图9 加载制度示意图Fig.9 Loading system diagram

3 结果分析

3.1 抗震性能随配筋率的变化规律

如图10所示为不同配筋率各模型的滞回曲线,即模型S1-0.64、S1-0.96和S1-1.29的滞回曲线。模型S1-0.64正向和负向的峰值承载力分别为575.39 kN和-587.47 kN,对应的位移角分别为1.50%和-1.65%。模型S1-0.96正向和负向的峰值承载力分别为704.89 kN和-716.33 kN,比模型S1-0.64的正向和负向峰值承载力分别大22.5%和21.9%。达到峰值承载力对应的位移角分别为2.18%和-2.00%。模型S1-1.29正向和负向的峰值承载力分别为791.98 kN和-802.91 kN,比模型S1-0.64的正向和负向峰值承载力分别大37.6%和36.7%,达到峰值承载力对应的位移角分别为2.28%和-2.00%。通过对比S1-0.64、S1-0.96和S1-1.29的滞回曲线可以看出峰值承载力及大位移角下的承载力随着PSB筋材配筋率的升高而增大。这是因为PSB筋材屈服强度高,在较大位移角下PSB筋材仍具有较大的应力,而普通钢筋屈服强度较小,这就使得PSB筋材混凝土柱在大位移角破坏时的水平力要大于普通钢筋混凝土柱。

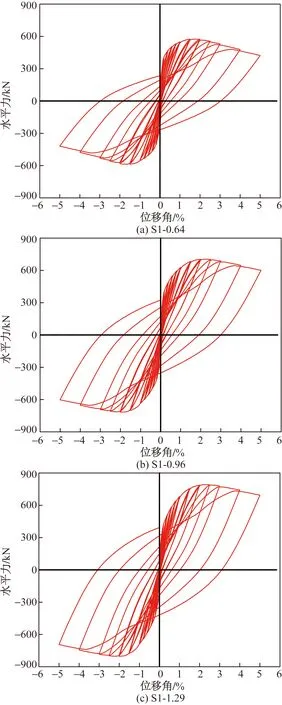
图10 不同配筋率的滞回曲线Fig.10 Hysteresis curves of different reinforcement ratios

滞回曲线中滞回环所包围的面积反映构件耗散的能量,表征构件的耗能能力。采用累积耗能[20]对模型的耗能性能进行量化分析,如图11所示。在位移角不大于1.5%时,各模型的累计耗能接近,曲线基本重合;在位移角大于1.5%时,模型的耗能能力随着PSB配筋率的增大而增大,在位移角为5.0%时,S1-0.64、S1-0.96和S1-1.29的累计耗能分别为164.69、205.81和239.98 kN·m,S1-0.96和S1-1.29的累积耗能相较于S1-0.64分别增大了25.0%和45.7%。这主要是由于在加载前期,模型受力较小,配筋率对模型的耗能影响不大,在较大位移角下,模型承受较大的水平力,配置更多的PSB筋材可以更好地耗散能量。

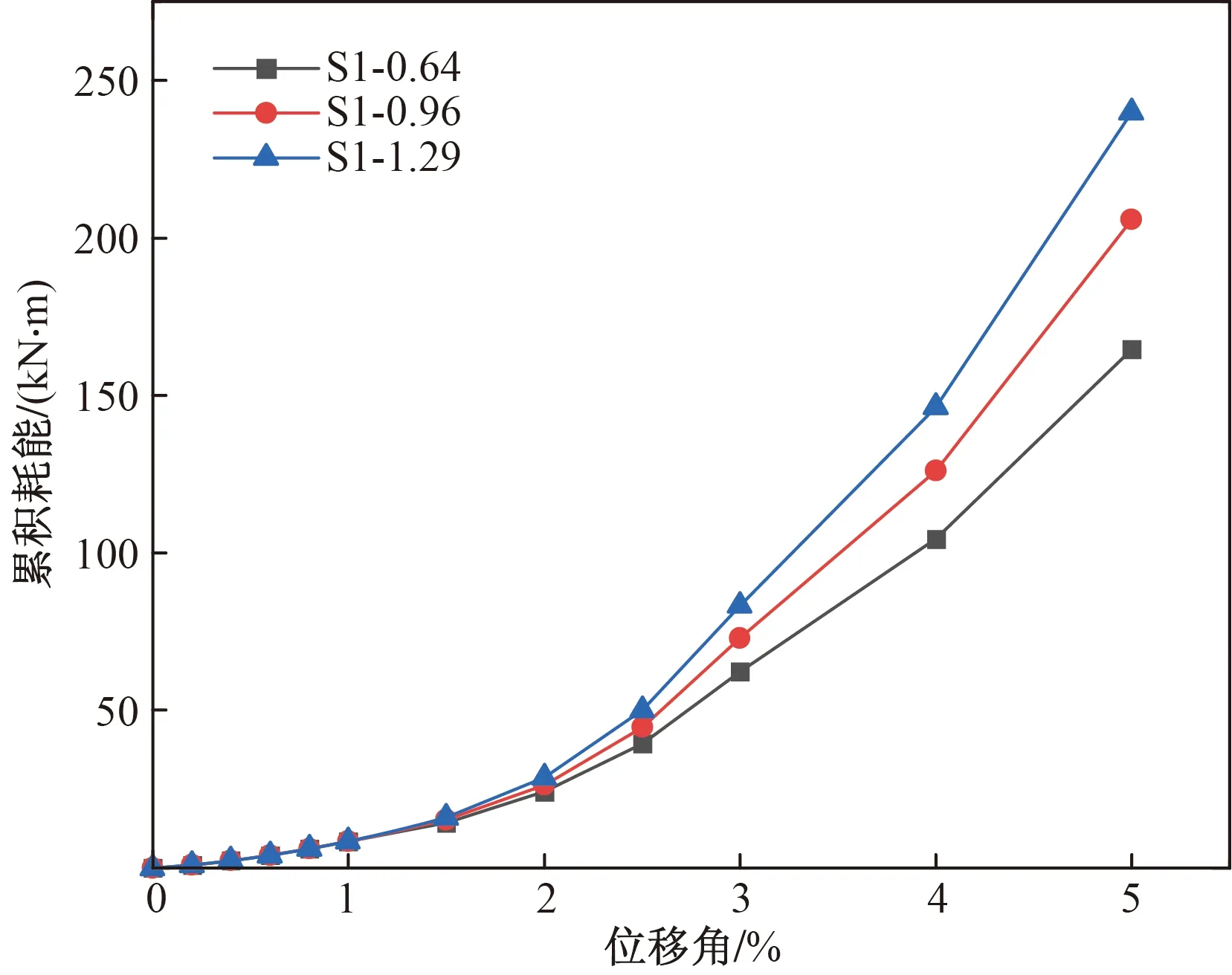
图11 不同配筋率的耗能曲线Fig.11 Cumulative energy dissipation of different reinforcement ratios

3.2 抗震性能随混凝土强度等级的变化规律

图12所示为不同混凝土强度等级各个模型的滞回曲线,即模型S2-40、S2-50和S2-60的滞回曲线。模型S2-40正向和负向的峰值承载力分别为646.32 kN和-653.81 kN,对应的位移角分别为2.35%和-2.23%,达到峰值承载力后水平承载力开始缓慢下降。模型S2-50正向和负向的峰值承载力分别为704.89 kN和-716.33 kN,比模型S2-40的正向和负向峰值承载力分别大9.1%和9.6%。达到峰值承载力对应的位移角小于模型S2-40,分别为2.18%和-2.00%,比模型S2-40的正向和负向峰值承载力对应的位移角分别小7.4%和10.1%。模型S2-60正向和负向的峰值承载力分别为764.27 kN和-778.33 kN,比模型S2-50的正向和负向峰值承载力分别大8.4%和8.7%。达到峰值承载力对应的位移角小于模型S2-40和S2-50,分别为2.00%和-1.83%。比模型S2-50的正向和负向峰值承载力对应的位移角分别小8.0%和8.8%。通过对比S2-40、S2-50和S2-60的滞回曲线可以看出模型峰值承载力随着混凝土强度的提高而增大,峰值承载力对应的位移角随着混凝土强度的增大而减小,在大位移角下的水平承载能力随着混凝土强度的升高而增强。

图12 不同混凝土等级的滞回曲线Fig.12 Hysteresis curves of different concrete grades

不同混凝土强度的累计耗能曲线如图13所示,在位移角不大于1.0%时,各模型的耗能能力接近,曲线基本重合;在较大位移角下,模型的耗能能力随着混凝土强度的增大而增强,在5.0%位移角时,模型S2-40、S2-50和S2-60的累积耗能分别为193.19、205.81和219.78 kN·m,模型S2-50和S2-60的耗能能力相较于模型S2-40分别提高了6.5%和13.8%。

图13 不同混凝土强度的耗能曲线Fig.13 Cumulative energy dissipation of different concrete strength

3.3 抗震性能随轴压比的变化规律

图14所示为不同轴压比各个模型的滞回曲线,即模型S3-0.2、S3-0.3和S3-0.4的滞回曲线。模型S3-0.2正向和负向的峰值承载力分别为680.81 kN和-683.67 kN,对应的位移角分别为2.45%和-2.33%,达到峰值承载力后水平承载力开始缓慢下降。模型S3-0.3正向和负向的峰值承载力分别为704.89 kN和-716.33 kN,比模型S3-0.2的正向和负向峰值承载力分别大3.5%和4.8%。达到峰值承载力对应的位移角小于模型S3-0.2,分别为2.18%和-2.00%,比模型S1-40的正向和负向峰值承载力对应的位移角分别小11.2%和14.0%。模型S3-0.4正向和负向的峰值承载力分别为687.52 kN和-695.64 kN,比模型S3-0.3的正向和负向峰值承载力分别小2.5%和2.9%。达到峰值承载力对应的位移角小于模型S3-0.2和S3-0.3,分别为1.50%和-1.50%。比模型S3-0.2的正向和负向峰值承载力对应的位移角分别小38.8%和35.5%。比模型S3-0.3的正向和负向峰值承载力对应的位移角分别小8.0%和8.8%。PSB筋材混凝土柱峰值承载力随着轴压比的升高并未发生明显的改变,达到峰值承载力对应的位移角随着轴压比的升高而减小,由于模型S3-0.4轴压比较大,在达到峰值承载力之后的水平力退化速度明显快于模型S3-0.2和S3-0.3。

图14 不同轴压比的滞回曲线Fig.14 Hysteresis curves of different axial compression ratios

不同轴压比的累计耗能曲线如图15所示。模型的耗能能力随着轴压比的增大而增强,在5.0%位移角时,模型S3-0.2、S3-0.3和S3-0.4的累积耗能分别为187.53、205.81和254.34 kN·m,模型S3-0.3和S3-0.4的耗能能力相较于模型S3-0.2分别提高了9.7%和35.6%。