基于强制环状流的往复式动态电导传感器的持液率测量
2023-11-04吴慧雄张兴凯李仲豪廖锐全
吴慧雄, 张兴凯*, 李仲豪, 廖锐全
(1.长江大学石油工程学院, 武汉 430100; 2.中国石油天然气集团公司气举实验基地多相流研究室, 武汉 430100;3.油气钻采工程湖北省重点实验室, 武汉 430100; 4.中国石油大港油田公司采油工艺研究院, 天津 300280)
在气液两相流的各项参数中,相含率是其特性的一个重要表征,对其他参数的测量起着至关重要的作用。两相流参数的准确测量对工业过程的合理性、经济性、安全性和可靠性具有很大的影响[1],对两相流参数进行实时准确测量的需求也越来越迫切[2],但是由于两相流动中气液流型的复杂性和随机性,在科学研究和应用领域中相含率测量长期未能得到良好的解决[3]。近年来,采用新型传感技术进行两相流流动的参数测量已经成为了专家学者们主要的研究方向[4-7]。由于工艺流程复杂,测量成本高等原因,这些新型技术并没有得到更好的推广应用。
中外学者针对两相流动及相含率测量已开展了大量研究,蒋亚莉等[8]为对气液两相流流动进行调整提出了一种新型的Ω形管并做出优化设计,为气液两相流动调整机理提供了较好的应用基础。邱思聪等[9]基于优化过的Y形组合式微通道结构进行了内部流场实验,结果表明,气液多相流流型对气液多相流混合的剧烈程度有显著影响,对混合效果有促进作用。杨伟霞等[10]进行了气液两相流在倾斜管中的流型转化边界,为气液两相流流型的判别提供了更为精确的依据。吕宇玲等[11]运用电导探针对气液两相流的持液率进行了实验研究,实验表明,与双平行探针相比,环状探针测量气液两相流相含率的效果更好。同年,Devia等[12]研究了平板电极和和双圆环状电极两种不同的电极结构传感器装置在气液两相流中相含率的测量,将实验结果与理论预测模型进行对比,结果表明,双圆环状电极结构测量结果较平板电极测量结果更为稳定。徐英等[13]为提高电容器对气液两相流含水率测量的能力,在电容传感器的测量单元基础上,增加旋转分相单元,克服了气液两相流动形态的多样性对持液率测量的影响。此外,传统电导法测量混合物的电导率,通过建立电导率-含水率关系模型实现相含率的测量,这种测量方法容易受到水的矿化度的影响,需对液相的矿化度进行实时的标定。
现通过利用旋流器将复杂多变的流型调换为强制环状流,进而将气液两相流中难以测量的液相分布转换成厚度较为均匀的液体薄膜测量,消除流型对两相流动中持液率测量的影响。自主设计一种新型的可进行往复运动的动态电导探针结构,设计出测量电路系统,进而对形成的均匀液膜进行远程在线实流测量,以弥补传统的直接电导测量装置仅能测量静态液膜厚度的不足。
1 电导法测量
1.1 强制旋流装置
气液两相流在测量管段上游,通常是以分层流、结构不对称的环状流等流型存在,在测量管段中加入叶片式旋流器,如图1所示,可在进行液膜测量时将不同流型强制调换成为液膜分布较为均匀的环状流。由于气液密度的差异,在离心力作用下,密度较大的液体被甩至管壁,形成一段均匀对称的液环。此时两相流以“液膜-气核”的状态存在于测量管段内,便可以采用往复式动态电导探针实现液膜厚度的在线实流测量。

图1 叶片式旋流器Fig.1 Vane type cyclone
1.2 电导测量原理
基于李仲豪等[14]采用的周向阵列电导探针测量装置,设计出了往复式动态电导传感器在线实流测量装置,利用水和空气导电率的差异性,当电导探针的金属尖端接触导电液体时,电路形成回路,电压信号采集器输出高电压;当金属尖端与导电率极小的气相接触时,回路电阻极大,电压信号采集器输出低电压[15]。测量原理图如图2所示,通过探针的往复运动深度获得不同的电压信号,进而计算出液膜的厚度。
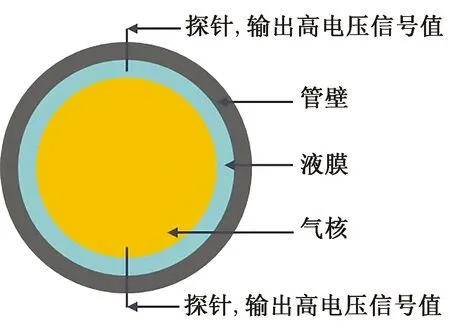
图2 电导测量原理图Fig.2 Schematic diagram of conductance measurement
2 数值模拟研究
2.1 数值模拟方法
采用计算流体力学软件Fluent进行数值模拟求解。模拟时模型的结构和网格划分质量对其结果的可行性、收敛性和计算精度有着直接的影响,使用Mesh进行模型的网格划分,采用结构化和非结构化的混合网格并进行网格无关性验证,确定最终网格数量为1 260 038个。采用欧拉模型(Eulerian)的多相流模型,该模型在不同体积分数的流体混合相中可计算出单相的流速等相关物理量[16]。湍流模型采用考虑了多相流动中具有旋流效应的雷诺应力模型(Reynolds stress model,RSM),该模型在具有叶片式旋流器的数值模拟中精确度更高[17]。
边界条件设置为速度入口以及压力出口,模拟介质为空气和水。模拟的方案如表1所示。
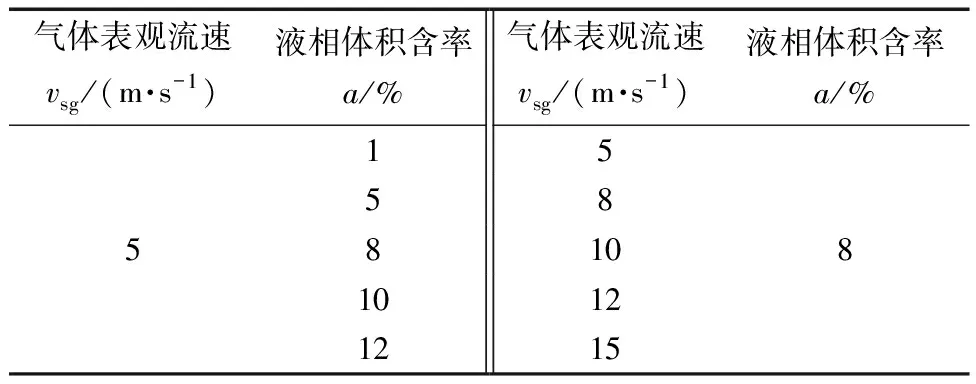
表1 数值模拟方案表
2.2 数值模拟结果分析
2.2.1 强制环状流流型
对内径为40 mm,长度为1 000 mm的测量管段进行数值模拟分析,以a=5%,vsg=8 m/s为例,观察在测量管段气液两相混合物流经旋流器后的形态分布,如图3所示。
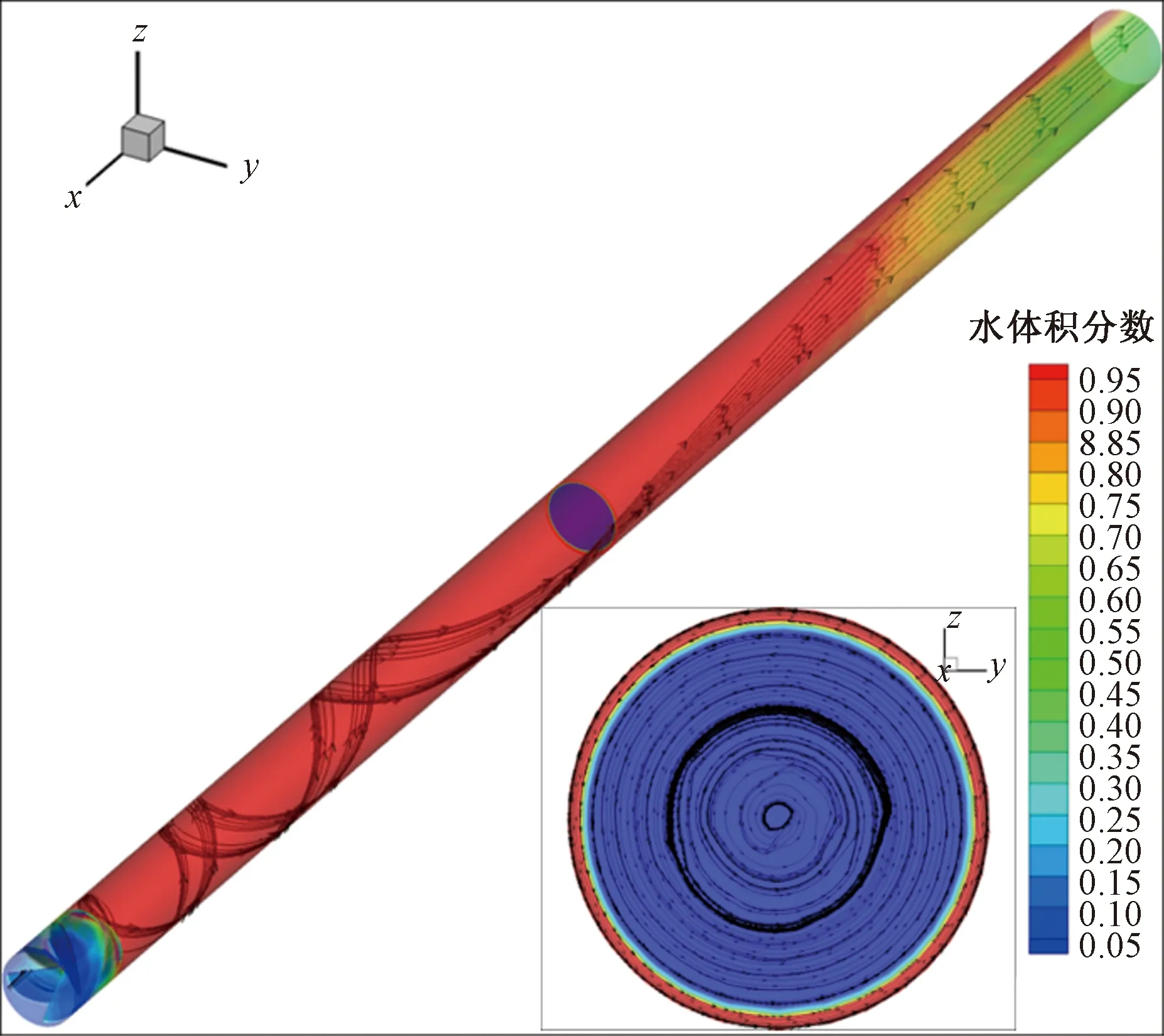
图3 旋流器管流体迹线图Fig.3 Cyclone tube fluid trace map
在混合相进入旋流器前壁面处,液相含率几乎为零,流态为湍流。在旋流器后端,壁面出现分布均匀的液膜,但随着管段长度的增加,流体流动迹线逐渐从螺旋流动转换成直线流动。在旋流管段内选取一管道截面,在旋流器的作用下混合相被强制转换为环状流,旋流效果较好且贴近壁面的液膜厚度分布均匀,形成了“气核-水环”的状态,达到了很好的气液分离效果。由于在旋流器下游流型变化较快,因而在使用电导探针往复运动测量持液率时,需将测量装置设置在测量管段中旋流效果较好的位置。
2.2.2 探针测量位置标定
采用网格体积含液率(即单位网格的液相含率)对数值模拟结果进行分析,即考虑网格单元液相分布来对液膜是否稳定形成进行分析。当测量管段内壁面液相含率高于90%,即认为已经形成液环[18]。为精确研究流体域内部混合相的流体流动状态,标定探针测量位置,以a=8%,vsg=8 m/s为例在旋流器下游的50、150、250、450、650、950 mm处选取截面进行研究,如图4所示。

图4 不同截面处液相体积分数分布 Fig.4 Liquid phase volume fraction distribution at different cross sections
从图4中可看出,在旋流器下游50 mm处已形成液膜成分布均匀的环状流,随着管道长度的增加至250 mm处,液膜厚度一直在不断增加,在旋流器的作用下混合相的流型得到充分的发展。随着长度的增加,在下游450 mm处,受重力影响,截面顶端液膜变薄,底部液膜变厚。在流体域后半段 650 mm 处至末端950 mm处,液膜衰减更加显著,液相分布不均匀性增加,在末端截面处已无法形成完整的液膜,这是因为随着管道长度的增加,气相流速降低导致气相携液能力降低,切向流速降低导致液相剪切力减小无法形成涡流,同时液滴受到重力在管道底部聚集,最终形成液相分布不均匀甚至消失的现象。
为研究管道贴近内壁处液环变化规律,在贴近管壁处取一条与管壁平行的直线可得到管道内壁处轴向网格体积含液率变化规律。由此可得出液环的稳定距离在旋流器出口196~302 mm处,即旋流器下游5D~7D(D为测量管段内径),且在250 mm(约6D)位置处含液率最大,液环最为均匀,因此在250 mm处标定为往复式动态传感器探针的测量位置。
3 往复式动态电导传感器测量系统
3.1 往复移动测量装置设计
为实现在动态实验测量过程中探针的往复可移动性,自主设计了一套可在线往复移动的电导探针装置,该装置主要由探针自动推进装置及远程控制器两部分构成,如图5所示。

图5 往复移动测量装置Fig.5 Reciprocating moving measuring device
3.2 测量电路系统
在利用电导法进行持液率测量所需要考虑的仅为电路是否导通,不需要考虑金属极化作用导致的测量误差。因此采用直流稳压电源提供电能,节能环保。测量电路主要由探针测量、电源跟随、数据采集器及计算机4部分构成,将电导探针作为测量电路的负极,钢制管段作为正极,当探针进行测量时,其与钢制管段形成闭合回路。随着探针的不断前移,接触到液体时,会输出高电压信号值;接触到气芯时,会输出低电压信号值,以此循环往复。其测量电路如图6所示。
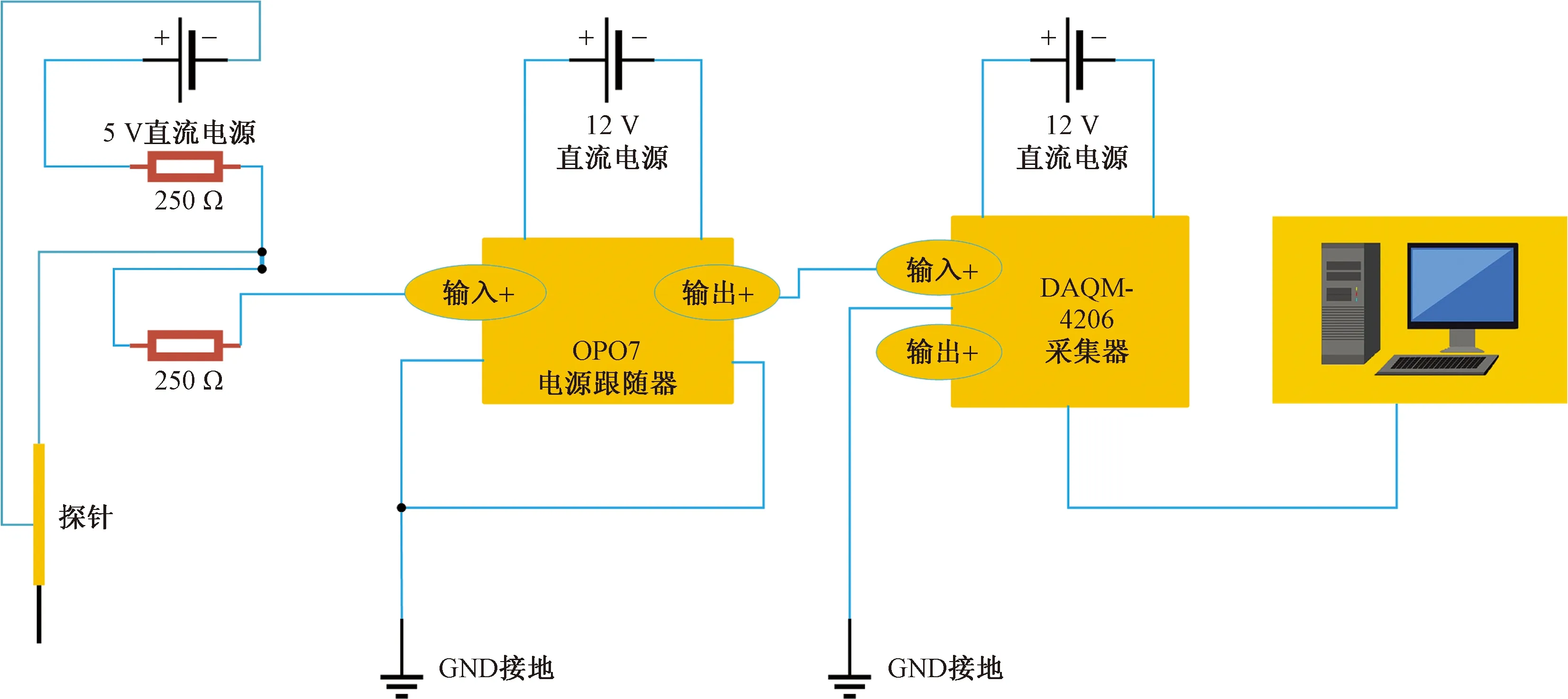
图6 电导测量电路图Fig.6 Conductance measurement circuit diagram
4 实验研究
4.1 实验设备与流程
4.1.1 实验设备
实验是长江大学的中国石油气举实验基地多相管流实验室进行装置设计、安装并实验的,该装置可分为气体供给系统、液体供给系统、计量装置、水平管实验测量管段、分离器、计算机控制系统、信号采集系统及计算机构成的,实验装置的流程图如图7所示。

图7 液膜厚度测量实验装置流程图Fig.7 Flow chart of liquid film thickness measurement experiment
在进行实验进行测量时,采用空气和水作为实验介质,同时向水中添加可溶性强电解质,以增强液相水的导电性。实验中,分别对气液两相进行增压混合,在各支路上分别配备流量计、温度计及压力计便于及时对气液两相流体的物性参数进行数据采集,另外,各支路上均安装单向阀以防止由于气相流量过大导致液相回流的现象。气液两相在被输送到混合器中进行充分的混合,而后输送至水平测量管段进行液膜厚度测量,最后经过气液分离罐进行气液分离,液体被送至储水箱中进行回收再利用,气体则直接被排入大气中。循环实验中,气液两相的流量通过Labview软件进行调控,气相增压使用单螺杆式空气压缩机,其可以提供的流量为0~2 300 m3/h;气相的流量测量使用热氏质量流量计,可以测量的流量范围为5~400 m3/h,测量的精度为±1.5%。液相增压采用多级离心泵,其可以提供的流量范围为0~6.3 m3/h;液相的流量测量使用转子流量计和电磁流量计,转子流量计测量范围为0~0.4 m3/h,测量精度为±1.5%;电磁流量计测量范围为0.3~3 m3/h,测量精度±0.5%。充分混合的气液两相进入水平测量管段内,流经叶片式旋流器后形成了一定长度的稳定环状流,将往复式动态电导传感装置安装在稳流段中,经过数据采集系统输出相应的电压信号值,记录时间为1 min。测量管段实验装置如图8所示。

图8 往复式动态电导传感器在线测量实验装置Fig.8 Reciprocating dynamic conductance sensor on-line measurement test device
实验在气液水平管道上进行,实验工质为空气和水,实验中气体的流量范围为22.6~90.5 m3/h,液体的流量范围为0.4~2.2 m3/h。具体实验方案如表2所示,信号采集电路激励电压为5 V直流电压。在进行测量实验之前,需要对整个实验系统进行密封检查,确保实验过程中装置不泄露。

表2 实验方案表
4.1.2 实验流程
当液相含率高于90%时,可认为液环已形成,
因此阈值R取90%,动态实验测量平均液膜厚度具体实验流程如下。
步骤1利用远程控制器调节探针的插入深度,当电压采集模块输出值高时,记录此时探针尖端与测量管段的距离H。
步骤2计算、记录每次采集时间内输出高电压信号的占空比M。
步骤3调节控制器,使电导探针继续前移Δh。
步骤4将M值与阈值R进行比较,当M 步骤5计算得出测量点处动态液膜平均厚度。 4.2.1 平均液膜厚度测量 对数值模拟所设计的10种工况进行实验测量,其测量结果采用占空比加权平均厚度算法[19]进行处理分析,测量统计时间内平均液膜厚度计算公式为 (1) 式(1)中:δavg为平均液膜厚度,mm;T为总采样时间,s;h为液膜高度的瞬时值,mm。 探针在进行动态测量时,其插入不同深度时所采集到的信号波形图不同,d1、d2、d3分别表示当前状态下的液膜平均厚度,如图9所示。当探针针尖与液膜接触时,测量电路处于导通状态,可输出高电压值信号即电源电压5 V,针尖未接触液膜时输出电压为0 V,当保持一定的测量时间时,随着时间的变化电压输出为电源电压的时间所占比值不同,表现为不同的占空比,因此输出信号表现为高低电平交替出现。 图9 探针不同插入深度测量示意图Fig.9 Schematic diagram of different probe insertion depth measurement 由于流体的不断向前运动,因此在电导探针往复运动的情况下,无法在不同的深度下进行同一个流体波的液膜厚度的测量,但是在测量管段前端放置的旋流器会将复杂的流型强制转换为环状流,同时,在足够长的采样时间的情形下,探针测量深度不同时所输出的测量信号值便可认为时不同深度下的平均液膜厚度。 从微观波形图进行数据分析,如图10所示,根据式(1)可计算出平均液膜厚度为 L1为波面;L2为在实验的测量时间段内气液界面的最小高度值;L3为管道内壁;Tλ为信号采集总时间,s;h1、h2、h3、h4分别为4个探针针尖至管道内壁底端的高度值,mm;t1、t2、t3、t4分别为4个探针对应的导通时间,s δavg=[h1(t1-t2)+h2(t2-t3)+h3(t3-t4)+h4t4]/Tλ (2) 式(2)中:t1/Tλ、t2/Tλ、t3/Tλ、t4/Tλ分别为不同测量高度值所对应的占空比Mi。换算出加权平均厚度算法公式如式(3)所示。在实际动态实验测量过程中,可依据对测量精度需求的不同,选定不同的电导探针插入深度增量。 δavg=MH+(H-Δh1)(M2-M1)+(H- Δh1-Δh2)(M3-M2)+…+(H-Δh1- Δh2-…-Δhi)(Mi+1-Mi) (3) 式(3)中:H为初始探针针尖处至管道内壁底部的高度,mm;Δhi为探针插入深度的增加值,mm。 因为所设计的往复式动态电导传感器在线测量装置测量精度可达到0.000 312 5 mm,因此无需考虑测量过程中产生的不确定度对测量结果的影响,极大程度上提高了测量精度,简化了测量流程。 4.2.2 平均液膜厚度理论计算 对测量管道内液膜平均厚度进行理论计算,通过已有数学模型预测液膜厚度的变化值,进而可对加权平均液膜厚度计算方法的测量误差方法进行评估,同时也验证了在强制环状流下设计的往复式动态电导传感器进行持液率测量的装置的可行性。 在强制环状流状态下,旋流器下游会形成一段气芯内没有液滴的环形流型,将液膜简化为理想的均质膜。通过简化液膜示意图中液膜与管道中心气芯的几何关系,利用式(4)和式(5)计算得到液膜的平均厚度。 (4) δavg=R2-R1 (5) 式中:R1和R2分别为气核半径及管道半径,mm;ε′和δavg分别为简化液膜模型计算的空隙率和液膜平均厚度,mm。令ε′=ε,那么可将式(4)代入式(5),从而可得到平均液膜厚度的计算公式为 (6) 4.3.1 占空比计算结果分析 对采集模块输出电压、时间进行处理,并计算出一定时间内高电压值输出的占空比,以气相表观流速5 m/s、液相体积含率8%工况为例进行分析。随着电导探针针尖距管道底端距离的改变,电压信号输出发生较大改变,为在动态实验过程中足够长的信号采集时间,截取60 s内的测量数据,如图11所示为获得占空比。 图11 不同液膜高度h处测量输出信号图Fig.11 Measured output signal diagram at different liquid film height h 从图11可看出,在采集模块输出高电压值初始阶段,其占空比较小,这是因为此时针尖距离管道底部距离较大,随着混合相向前流动仅有少部分的液膜波峰区域可与探针针尖接触导通电路。 通过不断调节自动电导探针的移动距离,随着针测量尖与管道底部之间距离的缩短,在固定时间内液膜与针尖的接触时间增加从而使高电压值占空比增加,如图12所示。测量过程中出现了非导通现象,这是因为强制环状流形成的液膜中存在少量气泡造成的,因此认定当占空比大于等于90%时,便形成了稳定的液环。 图12 不同液膜高度h处高电压值占空比Fig.12 Duty cycle of high voltage values at different liquid film height h 4.3.2 液膜厚度实验及理论计算结果分析 采用加权平均厚度算法分别对10种工况下液膜厚度进行了测量计算,研究了在气相表观流速不变,液相体积分数对液膜厚度值的影响;保持液相体积分数不变,气相表观流速对液膜厚度值的影响,结果如图13所示。 图13 不同工况下液膜厚度实验测量值与理论值对比图Fig.13 Comparison of experimental and theoretical values of liquid film thickness under different working conditions 由图13可以看出,利用控制变量法,气液比保持不变,且保持液相体积分数恒定,随着气相表观流速的增大,实验管中液膜厚度在逐渐增大,这是由于随着气体表观流速的增加,气相不断地携带液体,致使单位体积内持液率越来越大;其次在气相表观流速较低且不变时,随着液相体积分数的增加,液膜厚度会逐渐增大,但是液膜厚度增加的速率较小,这是由于当气相体积流量较小的时候,致使气相表观流速会较小,其能够携带液相的能力较差,虽然液相体积分数在不断地增大,但是气相所携带的液体没有显著增加,因此液膜厚度并没有明显变厚。当流动过程中气相体积流量较大时,随着液相体积分数的增加,液膜厚度有了明显的增厚,因为随着气体流量的增加,其携液能力会逐渐增强,导致旋流后两相分离出来的液相增多而使液膜变厚。 对比液膜厚度实验值与理论值,可以得到两种不同情形下的液膜厚度的偏差,如图14所示。 图14 不同工况下液膜厚度实验测量值与理论值偏差Fig.14 Relative error between experimental and theoretical values of liquid film thickness under different working conditions 通过图14可知,液膜厚度的理论计算值大于实验测量值,最大偏差分别为8.90%和10.45%。这是因为利用的理论计算模型中忽略了旋流装置所带来的偏差。当气液两相流流经旋流器后产生强烈的涡流,计算过程忽略旋流产生的离心力及黏性力、涡量产生的损耗。此外,通过对比偏差值可发现,随着气相表观流速的增加,偏差也随之增大,这是因为较高的气相流速对液相的携带作用增强,但在理论计算过程中未考虑强制环状流形成的“液膜-气核”中气核中心携带的液滴。因此,液膜厚度理论值与实验值会存在一定偏差。 (1)通过数值模拟研究,研究了气液两相流在经过旋流器后形成的强制环状流流型,液环的稳定范围维持在旋流器下游196~302 mm,且标定了动态电导传感器进行液膜测量的位置位于旋流器下游250 mm(约6D)处,此处的液相含率最大,液环最为均匀。 (2)针对传统直接电导法测量两相流中液膜厚度仅能静态测量的问题自主研发设计了基于强制环状流的往复式动态电导传感器装置,可针对液膜厚度进行远程在线实流测量,有较好的工程实际应用价值。 (3)通过实验所得数据进行占空比计算以及理论计算可知,保持实验过程的气液比不变,且保持液相体积分数恒定,随着气相表观流速的不断增大,实验管中液膜厚度在逐渐增大;在气相表观流速较低且不变时,随着液相体积分数的增加,液膜厚度会逐渐增大,但是液膜厚度增加的速率较小;当流动过程中气相体积流量较大时,随着液相体积分数的增加,液膜厚度有了明显的增厚。 (4)在理论计算中忽略旋流装置带来的偏差影响,使得液膜厚度的实验测量值小于理论计算值,在保持气相表观流速不变与液相体积分数不变两种情形下的最大偏差分别为8.90%和10.45%,在实验过程中,可通过调节不同插入深度以达到需求的精度。4.2 实验及理论计算方法




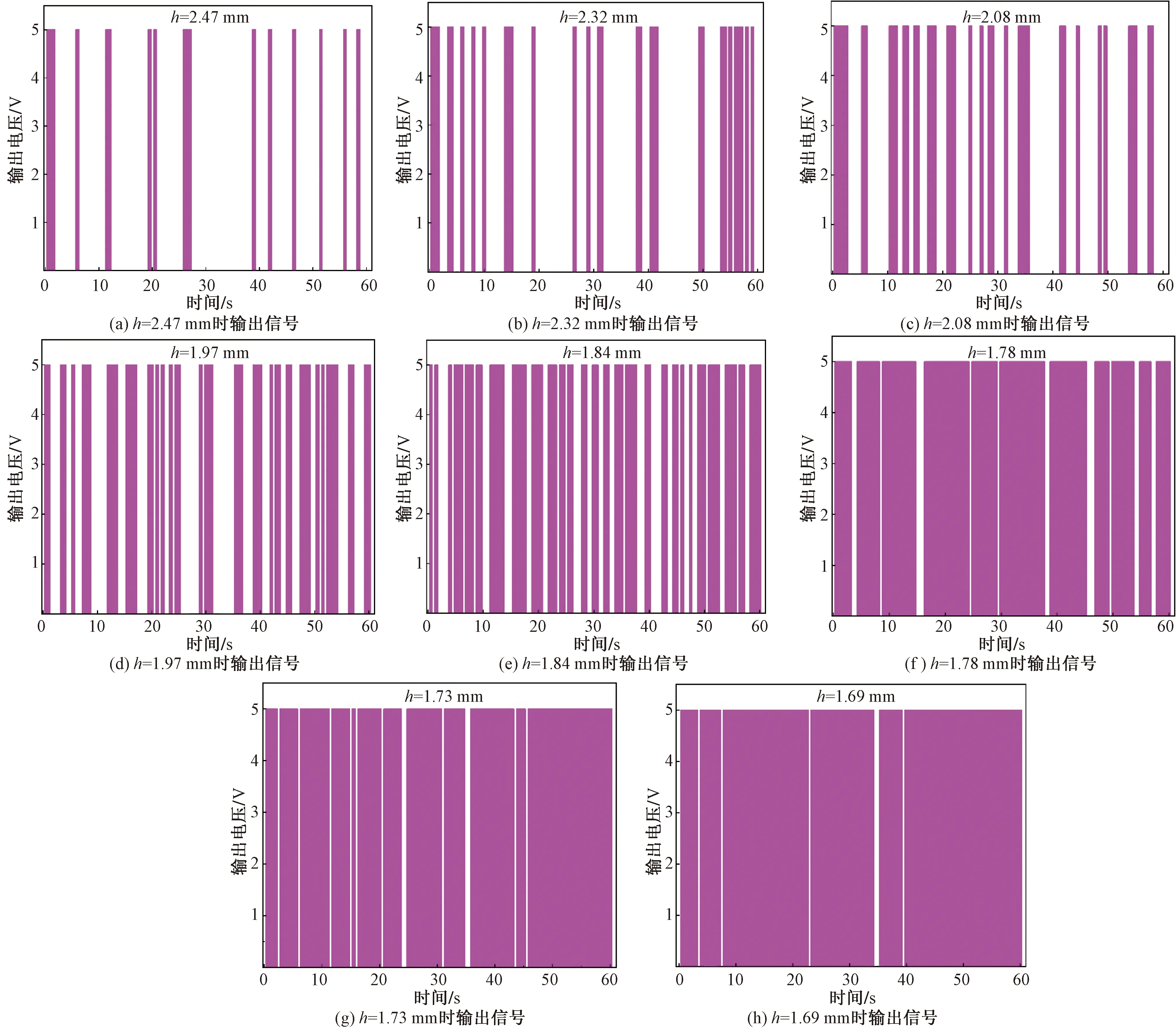
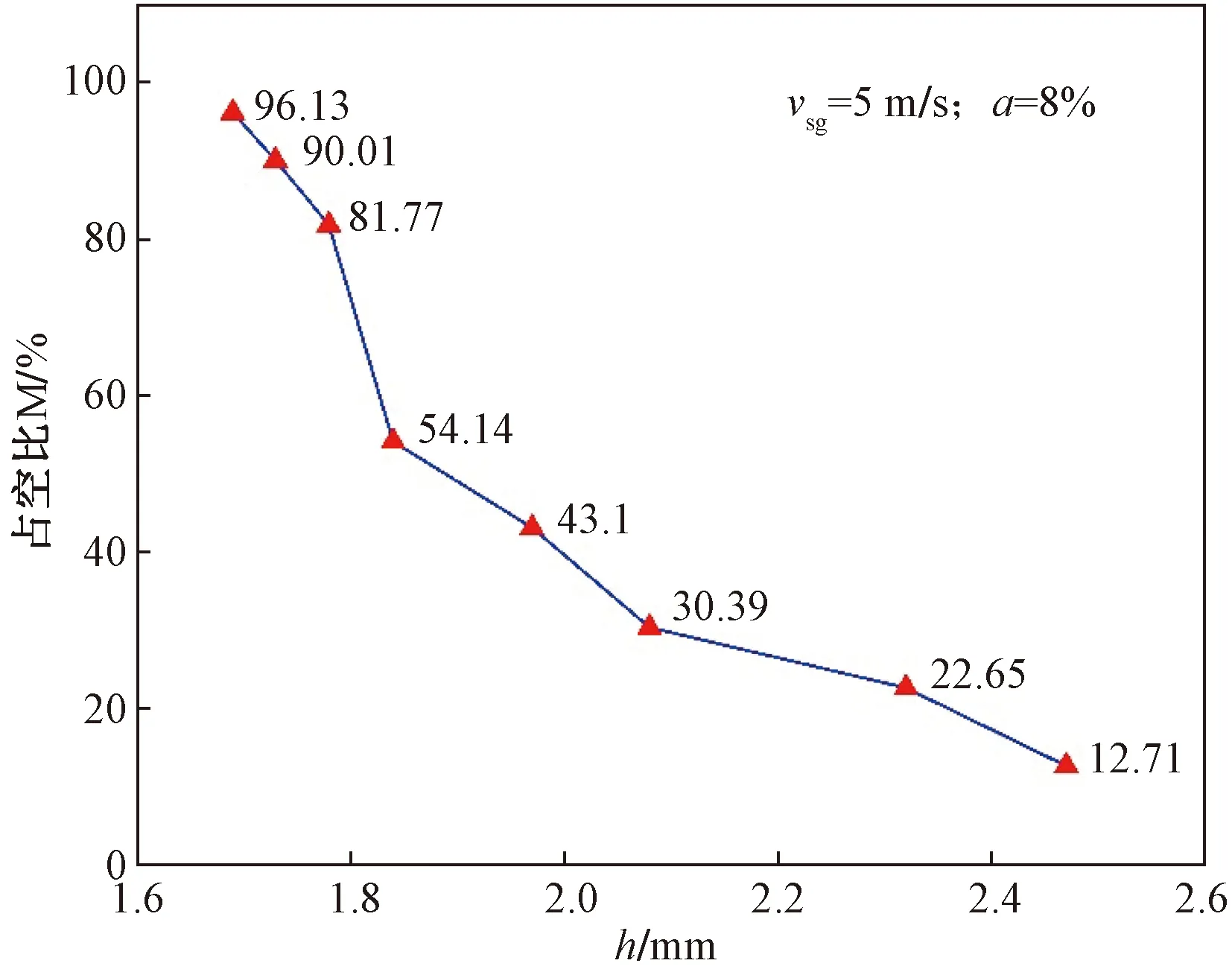
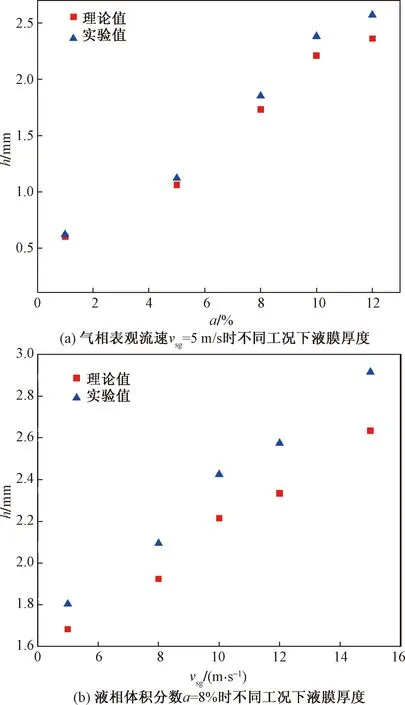
4.3 液膜厚度实验结果分析

5 结论
