凹凸酒窝表面换热管道内颗粒沉积与传热特性的数值模拟研究

韩尊师, 卢 浩,3,*, 赵文君, 王泽宇, 肖志博

(1. 新疆大学 电气工程学院 能源碳中和实验室, 新疆 乌鲁木齐 830047;2. 新疆大学 西北能源碳中和教育部工程研究中心, 新疆 乌鲁木齐 830047;3. 新疆大学 未来技术学院 新能源研究中心, 新疆 乌鲁木齐 830047)

0 引 言

热交换器广泛应用于能源利用领域,包括加热和冷却系统在内的各种设备都需要在气流和热交换器表面之间进行热传递[1-2]。然而,在长期使用过程中,湍流携带的颗粒会沉积在热交换器表面。这将导致传热效率的大大降低,同时还会增加热交换器的压降[3-4]。因此,了解颗粒如何附着在热交换器表面非常重要。

研究方法在数值模拟研究中非常重要,研究方法的不同往往会对研究结果产生一定的影响。XU等[5]对比了拉格朗日技术和欧拉技术在相同运行环境下预报湍流中颗粒沉积的效果。结果表明,欧拉技术的计算时间低于拉格朗日方法。KUMARI等[6]通过数值和实验研究,帮助理解了紧凑型热交换器的热力学特征,从而进行了有效的设计,并对热交换器管束进行热力、水力和空气动力测试,提出了具有不同翅片比的各种全尺寸管试样。

热交换器的结构会影响其传热性能。研究发现,可以通过优化和改进热交换器结构来实现热交换器的优化。HAN等[7-8]通过数值模拟的方法分别对凹酒窝换热管道和凸酒窝换热管道进行了研究。研究者采用了RANS方法对两种换热管到进行了仿真,RSM模型被用于流场的计算,结果表明与光滑管道相比凹酒窝和凸酒窝换热管道均可强化管道的换热且可以促进大颗粒的沉积。LI等[9]对U形弯曲带肋通道中的颗粒沉积进行了离散模拟。气相计算采用雷诺平均纳维-斯托克斯技术,结果表明后排肋条受到前排肋条的保护,较高的雷诺数和较大的颗粒直径促进了颗粒在壁上的沉积。

本研究的重点是分析热交换通道内结构的改变对通道中的流场和颗粒沉积情况的影响。模拟中研究了一种规律性凹凸酒窝热交换管道的换热和颗粒沉积情况。通过比较管道中有无凹凸酒窝存在以及改变入射颗粒大小,研究不同条件对管道中热交换特性和颗粒沉积特性的影响。

1 数值方法

1.1 气相湍流模型

雷诺应力模型(RSM)考虑了湍流的各向异性,可以计算出管道中由于应力引起的二次流,是Fluent中提供的最精细的RANS湍流模型。RSM采用求解雷诺应力输运方程以及耗散率方程而不是涡黏性假设来封闭方程。因此RSM模型在三维求解中需要额外求解七个方程[10-11],气流的质量、动量和能量方程可以描述为:

(1)

(2)

(3)

式中,ρ为流体密度,kg/m3;p为压力,Pa;h为焓值,kJ/kg;x,u,fi分别表示笛卡尔坐标分量、速度分量以及质量力的分量;μ为分子粘性系数;μt为湍流粘性系数,由湍流模型确定。

由于粗糙结构的存在,在壁面附近会出现一些复杂的湍流结构。本文为了准确地模拟粗糙流道的湍流流动,采用了RSM模型来对气相部分进行模拟,RSM模型相较于k-ε,k-ω这两种模型来说,RSM模型更多地考虑了湍流涡粘度的各向异性,而且它大大提高了计算的精度。

湍流雷诺应力模型(RSM)的方程表达式为:

(4)

式中σk,C1,C2是经验常数,分别为1.0,1.8和0.6。

湍流耗散率ε的计算公式为:

(5)

其中,σε= 1.3,Cε1= 1.44,Cε2= 1.92[12]。

1.2 离散相模型

颗粒在粗糙流道壁面沉积主要包括流场中的运动、与粗糙壁面的接触粘附或反弹、在流场的出口逃逸这三个过程,颗粒在流场中流动时主要受接触力(碰撞力和接触粘附力)、非接触力(非接触粘附力)、流体对颗粒的作用力(涡团区域的浮力、布朗力、Saffman升力和热泳力)以及颗粒自身重力的作用。因为空气密度与粒子密度之比非常小(本研究中为0.000 8),所以与粒子上的外力相比,压力梯度力和虚假质量力都很小,因此忽略这些力对颗粒的作用[13]。对于DPM模拟,研究采用了单向耦合。

DPM模型中考虑了颗粒相的传热过程,其中使用的颗粒物类型为惰性,其传热过程为惰性加热/冷却,离散相中还考虑了热泳力对颗粒物运动的影响。

根据拉格朗日轨道追踪法求解了颗粒运动方程得到其运动轨迹,颗粒的运动满足牛顿第二定律,平衡方程为:

(6)

其中mp为颗粒质量,kg;up为运动速度,m/s;等式右边依次为颗粒所受曳力、重力、布朗力、Saffman升力和热泳力。

在RANS模型中,离散随机漫步模型(DRW)考虑了颗粒的离散旋涡与流体之间的相互作用,从而能够更好地预测颗粒的湍流扩散。本研究采用雷诺应力模型(RSM),其脉动速度考虑了雷诺应力的各向异性:

u′=ζu′rms

(7)

v′=ζv′rms

(8)

w′=ζw′rms

(9)

在湍流涡团中,流体脉动速度u′、v′和w′ 满足高斯概率密度分布函数,m/s。ζ是正态分布随机数。

研究发现,如果直接应用DRW模型和RSM模型,会导致对颗粒沉积速率的过度预测[10, 14]。因为垂直于壁面的速度波动对于计算颗粒沉积速度是很重要的,Kim等的DNS数据[15]校正近壁区域的壁面法向湍流波动可以准确预测颗粒沉积速度。计算公式为:

(10)

(11)

(12)

其中v为运动粘度,m2/s;CC为坎宁安滑移修正系数(Cunningham slip correction coefficient);S为粒子与空气的密度比;dp为颗粒物粒径,μm。

与墙壁的无量纲距离y+的定义如下:

(13)

颗粒的沉积速度Vd由下式得出:

(14)

式中J是沉积的颗粒数量;C0是平均颗粒浓度,%(体积分数);颗粒的无量纲沉积速度[16]为:

(15)

颗粒沉积率的计算方法为:

(16)

其中Nd和N0分别为沉积颗粒的数目和管道入口释放的颗粒数目。

大寻访活动在深圳启动，作为晚到者，我在东莞加入了团队。加入之前，北京印刷学院的六位同学已经紧张地奋战了几天，一开始以为我会不适应，其实不然，在大家的照顾下我很快融入集体。第一天晚上，我便加入了大家的讨论，“怎样从大学生的视角来看待整个印刷行业？”几个人众说纷纭，也不知道哪位同学提到了凹（ao）印，我听着不顺耳，就顺便跟了句，我们业内都叫（wa）印，“看见没，这是专业的”，顿时紧张的氛围立马就欢快了起来。

2 工况描述及求解方法

图1(a)是凹凸酒窝管道XY截面结构化示意图,图1(b,c)为YZ截面结构化示意图。通道宽度D为20 mm,长度L为400 mm。通道的下表面排列着规律性的凹凸酒窝。通道下表面的凹凸酒窝为2×8,共16个。入口区位于通道前部,以确保凹凸酒窝结构附近的气流均匀,而出口位于通道后部,并在通道后部延伸,以避免空气倒流。根据表1,研究共模拟了16个实例。入口风速设为6 m/s,采用出口受压条件,通道壁面和凹凸面均设为无滑动条件。采用了第一类边界条件,规定通道壁面和凹凸酒窝面温度为300 K,入口热空气温度为373 K。

表1 仿真工况Table 1 Simulation case

研究中所采用的颗粒物为无烟煤颗粒,即“anthracite”,密度为1 550 kg/m3。50 000个颗粒在入口处以圆锥面(cone)方式入射,通道内地所有粒子都被追踪,直到它们沉积在管道中或离开管道。为了关注凹凸酒窝的存在对通道中颗粒沉积的影响,将凹凸酒窝和下表面的壁面边界条件设置为“trap”,即粒子一旦接触到上述两个壁面,即视为沉积。通道的出口是“escape”边界条件[17]。

采用有限体积法(FVM)求解湍流风场的控制方程。对流项和扩散项分别采用二阶迎风格式和二阶中心差分格式离散。采用SIMPLE算法对压力场和速度场进行解耦。采用龙格-库塔法求解尘埃粒子的运动方程。

3 模型验证

3.1 网格无关性验证

利用网格划分软件ICEM划分了凹凸酒窝通道的六面体结构化网格,并对边界层区域进行了加密处理,网格总数为1 717 561,壁面最近网格中心距离壁面3.3e-5m,增长因子为1.2,如图1所示。

为探究网格数量对仿真模拟的影响,对模型进行了网格无关性验证。分别挑选了网格数量为:802 455、1 096 544、1 543 431、1 717 561和1 949 675地5种网格数量的模型进行了验证,计算了颗粒粒径分别在10、30、50 μm时通道内的颗粒沉积率,如图2所示。结果表明当通道网格数量大于1 717 561时,网格数量对颗粒沉积的结果影响较小,因此本研究选用了网格数量为1 717 561的网格。

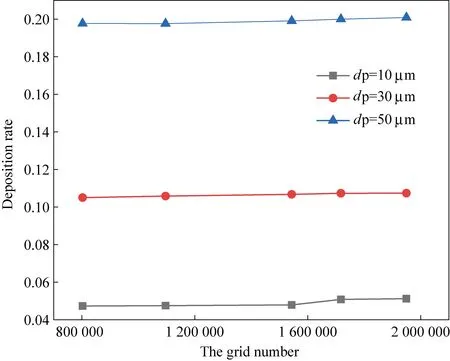
图2 网格无关性验证折线图Fig. 2 Line graph mesh-independence validation

3.2 流场验证

选择光滑管道中X=0.1 m处的湍流流速剖面,是因为此时流场已经完全演化[18]。如图3所示,本文RSM模型的计算结果与KIM等的直接数值模拟(DNS)结果非常吻合[15]。

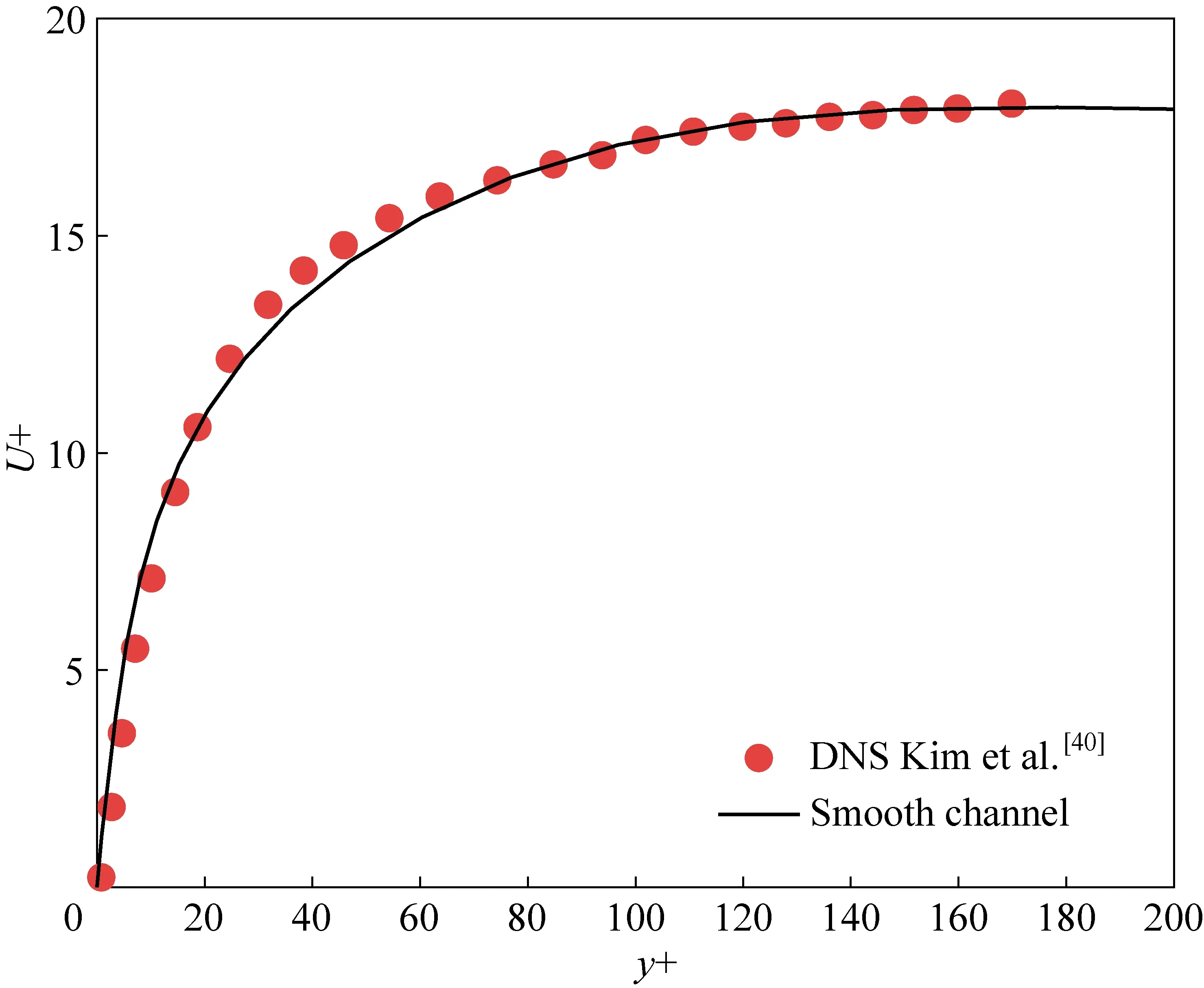
图3 光滑通道速度数值验证图Fig. 3 Numerical validation graph of smooth channel velocity

3.3 颗粒沉积验证

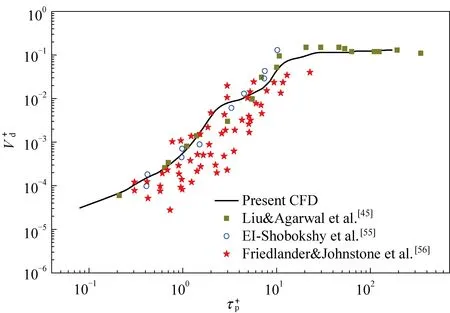
图4 光滑通道颗粒沉积数值验证图Fig. 4 Numerical validation graph of particle deposition in smooth channel

4 结果分析

4.1 通道流场分析

热交换通道中,凹凸酒窝的存在会极大地影响通道中的速度场和温度场,以及通道壁面处气流的流动状态。如图5(a)所示,从X=0 m处开始,可以明显观察到沿着凹凸酒窝的周期性速度边界层。在凹酒窝空腔内部气流速度较小,凸酒窝后方存在低流速区。在凸酒窝后面的凹酒窝空腔内的速度要大于左侧第一个凹酒窝空腔内速度,这是因为凸酒窝的存在影响了通道内的流场结构,为其后面的凹酒窝起到了引流的作用。

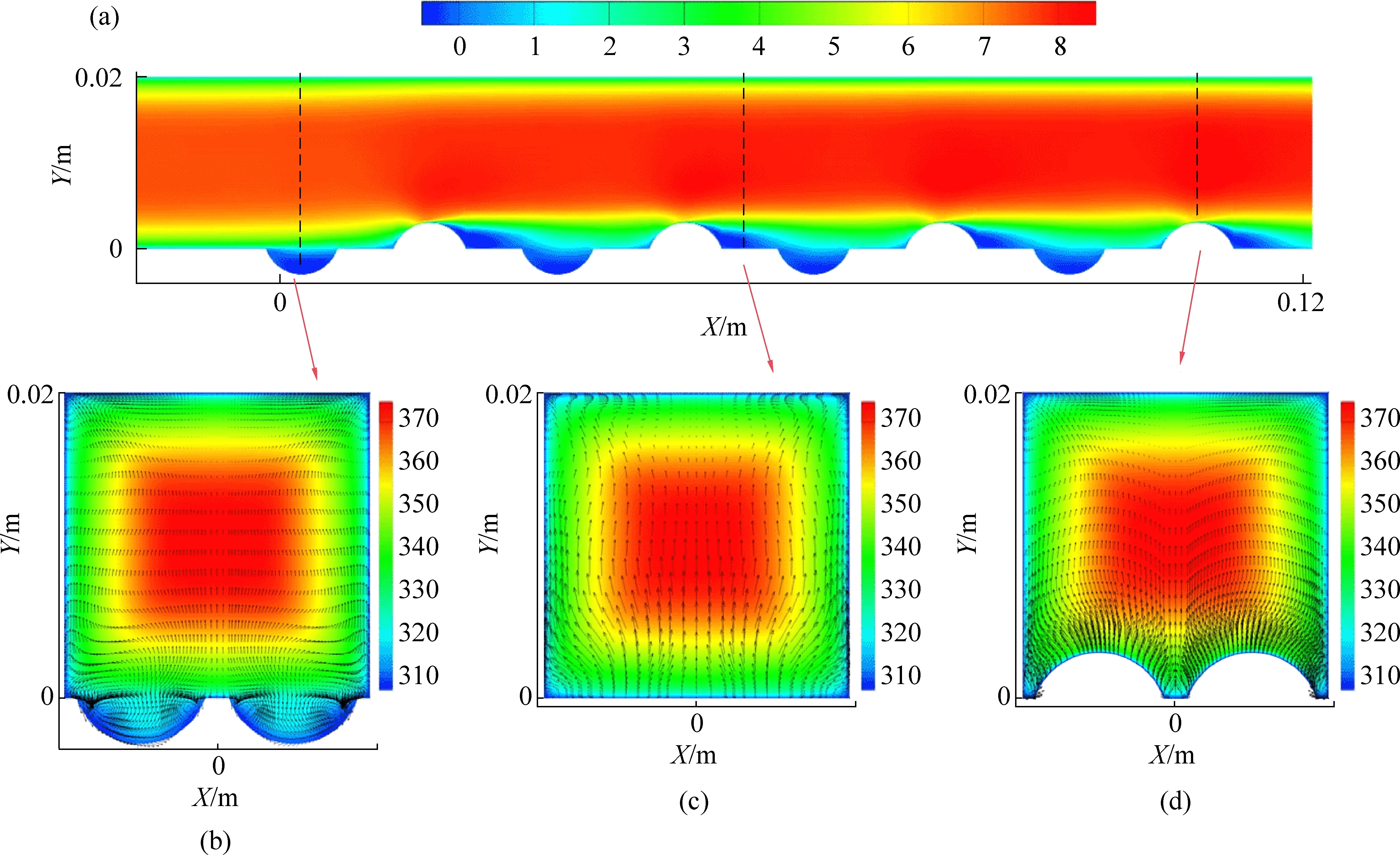
图5 (a)凹凸酒窝速度云图, (b,c,d)YZ截面温度场及二次流动示意图Fig. 5 (a) Velocity cloud of dimple and convex dimple,(b,c,d)Temperature field and secondary flow in YZ section

凹凸酒窝的存在还影响了通道内的温度场。如图5(b-d)所示,凹酒窝空腔内部是低温区,通道中部位置是高温区。温度由通道中部靠近壁面递减,此时则会存在由高温区域指向低温区域的热泳力,从而促进颗粒趋壁沉积。另外通过观察通道YZ截面的速度矢量图,在通道壁面处和凹酒窝空腔内部存在二次流动,可以促进颗粒物在此处的沉积。

图6展示了通道中YZ截面的TKE值(Turbulent Kinetic Energy)和流场流线图,高TKE值在凹酒窝的右上位置,凸酒窝的迎风面上方和背风面的后方。凹酒窝空腔内和凸酒窝后方存在明显的大涡团,高TKE值和大涡团的存在会极大地影响通道内的颗粒沉积特性。

图6 YZ截面TKE值及流场流线图Fig. 6 YZ cross-section TKE value and field streamline

4.2 颗粒沉积分析

通道中凹凸酒窝的存在会影响通道内的流场进而影响颗粒物在通道内的运动轨迹,图7为流场均匀时颗粒轨迹分布图,在凹凸酒窝上方颗粒物较密集而在表面光滑区域则颗粒物较分散。

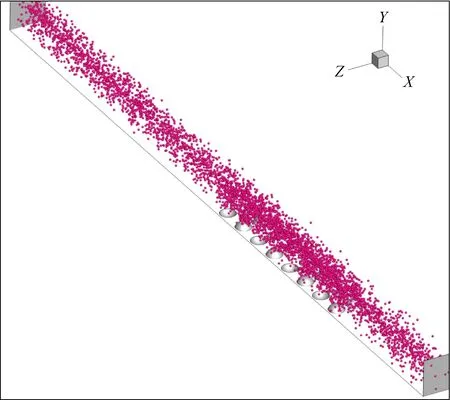
图7 凹凸酒窝通道颗粒轨迹图Fig. 7 Particle trajectory of dimple and convex dimple channel

在光滑通道内进行了颗粒物沉积实验,选用的是美国ISO 12103-1 A2灰尘,沉积情况如图8所示,同时跟光滑通道仿真对比,沉积形貌几乎一致,证明了本仿真模拟颗粒沉积模型的正确性。

图8 光滑通道颗粒沉积实验仿真对比图Fig. 8 Comparison of experimental simulation of particle deposition in smooth channel

图9展示了不同粒径的颗粒物在凹凸酒窝通道中的三维沉积示意图。图9(a)展示了粒径为1 μm的颗粒部分沉积在凹酒窝空腔内部和凸酒窝迎风面上,但是光滑表面处也有部分颗粒沉积。此时颗粒物质量较小,受流场影响较大,流场均匀后颗粒物沉积分布也较为均匀。图9(b)中5 μm颗粒集中沉积在凹酒窝空腔内、凸酒窝迎风面以及凹凸酒窝之间的光滑壁面。这是因为颗粒粒径增大,重力和颗粒自身的惯性对颗粒物的沉积影响变大,因此凸酒窝的迎风面沉积颗粒数目增多。图9(c)30 m的颗粒物主要沉积在凸酒窝迎风面以及第一个和最后一个凸酒窝两侧光滑壁面处。此时颗粒粒径进一步增大,受流场、重力以及颗粒物自己惯性的影响,颗粒物集中沉积于凸酒窝迎风面,凹酒窝右上部以及光滑壁面。

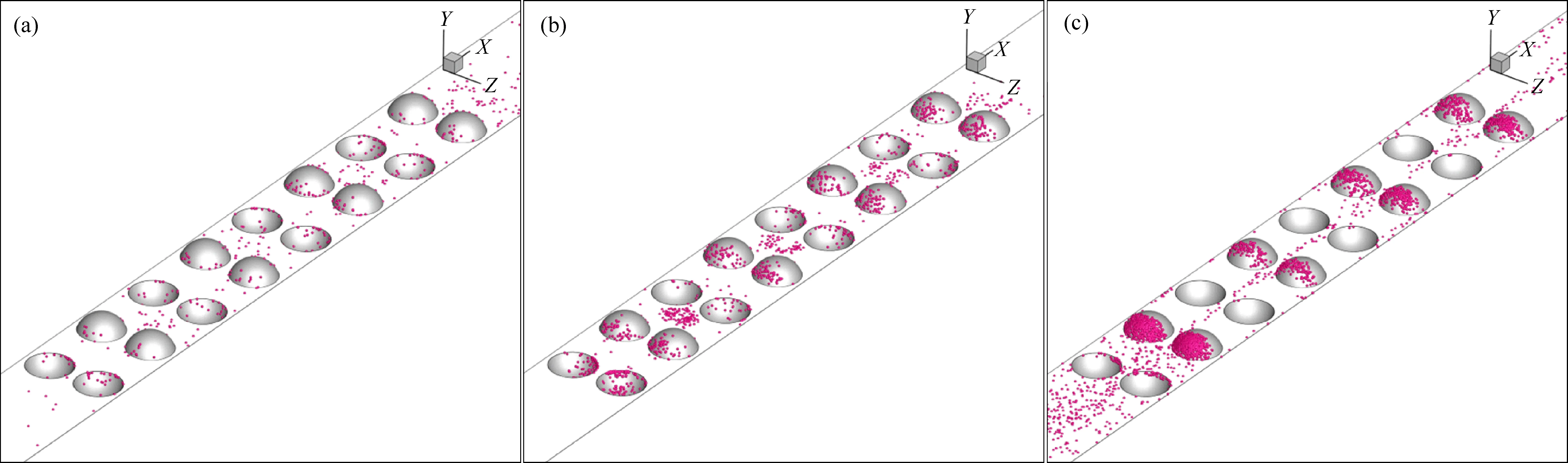
图9 (a,b,c)1、5及30 μm颗粒沉积示意图Fig. 9 (a, b, c) Schematic of 1, 5 and 30 μm particle deposition

当颗粒粒径较小时,凹凸酒窝通道内颗粒物沉积率大于表面光滑通道内。随颗粒粒径增大,总体颗粒物在通道中的沉积数目越多,然而两种通道中的沉积率趋于一致,当粒径增大到50 μm时凹凸酒窝通道中沉积率略低于表面光滑通道,如图10所示。

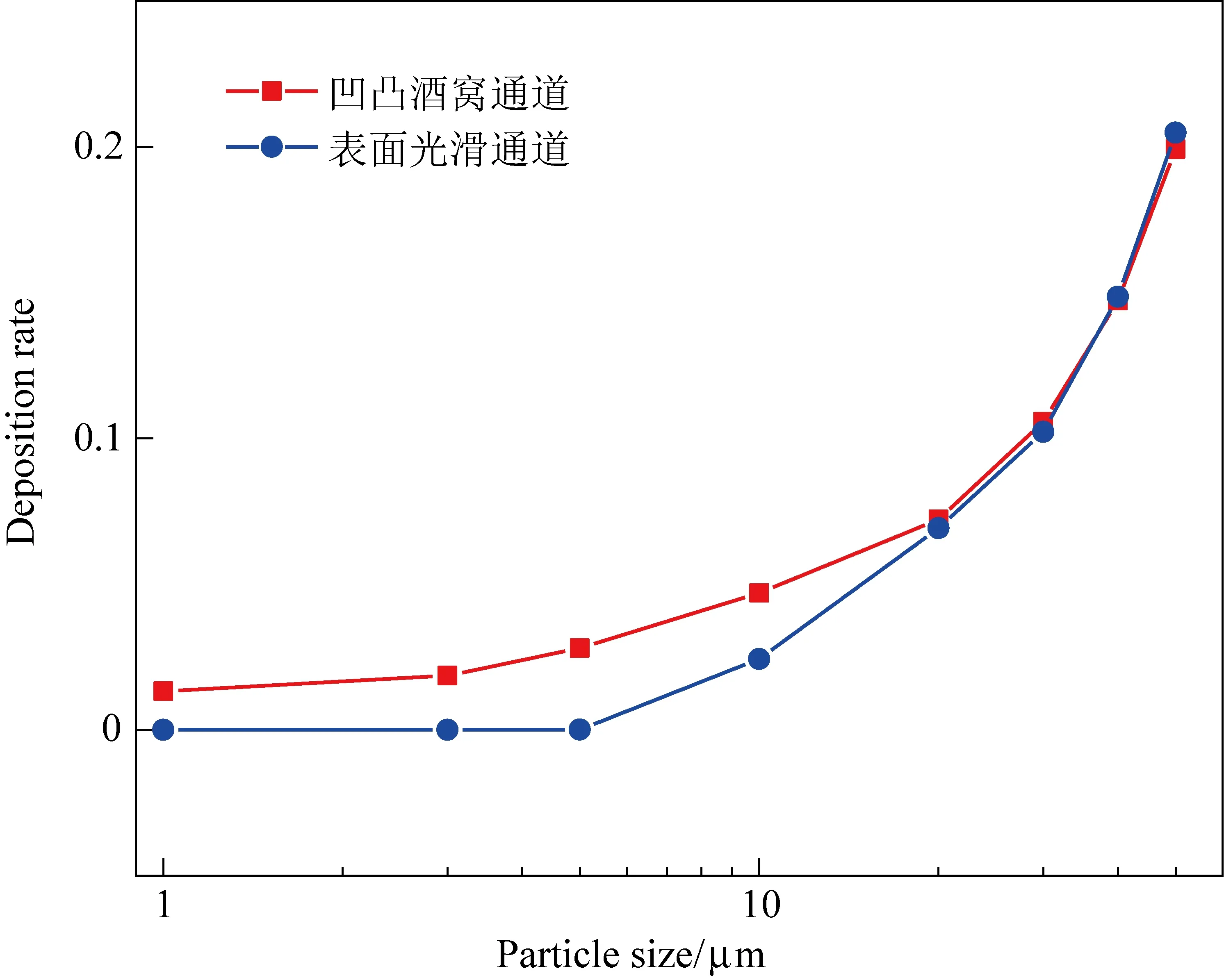
图10 通道颗粒物沉积率对比Fig. 10 Comparison of channel particulate deposition rates

5 结 论

研究了颗粒物在具有凹凸酒窝结构的三维传热通道中的沉积情况。采用了结构化网格进行了网格划分,流体相采用雷诺应力模型(RSM),颗粒相采用离散颗粒模型。研究并讨论了气流场、粒子沉积特性和沉积效率。研究了壁面结构和颗粒物对流场和沉积特性的影响。结论如下:

(1)凹凸酒窝的存在会影响酒窝通道中的流场,并强化通道中的传热。它还会影响颗粒在通道中的运动轨迹。更多的颗粒聚集在凹凸酒窝上方,酒窝的存在促进了小颗粒(dp≤10 μm)的沉积。

(2)颗粒粒径大小的差异会明显影响颗粒在通道中的沉积。颗粒沉积速率随颗粒直径的增大而增大,凹凸酒窝结构的存在对小颗粒(dp≤10 μm)的沉积有很好的促进作用。