节理几何特征对爆破裂纹扩展的数值模拟研究

2023-11-02费鸿禄包士杰蒋安俊

工程爆破 2023年5期

费鸿禄,山杰,包士杰,蒋安俊

(辽宁工程技术大学爆破技术研究院,辽宁阜新 123000)

钻爆法破碎岩体过程中,炸药爆炸后,爆炸冲击波作用于炮孔近区岩体,随着冲击波扩散距离的增加,冲击波逐渐减弱为应力波,应力波对岩体的破坏和裂纹的扩展起着非常重要的作用。在天然岩体中存在着大量的裂隙、层理、节理等结构面,结构面的存在导致岩体有明显的不均匀性和各项异性,当爆炸应力波遇到节理面时,不同节理几何特征产生的反射、透射、绕射应力波的区域与大小不一样,从而改变爆炸应力波对岩体的作用效果、破坏模式以及爆破裂纹扩展范围,最终改变岩体爆破效果。国内外学者对节理岩体爆破以及裂纹扩展规律进行了一些研究,刘婷婷等[1]通过数值模拟方法研究含充填节理岩体中应力波的传播规律,发现充填厚度的递增会降低透射系数,节理数量对透射系数的影响与节理间距有关;潘长春等[2]基于模型试验研究了含裂隙岩体爆破时,爆破振动波的传播规律,结果表明裂隙的存在显著降低了爆破振动效应;丁晨曦等[3]基于模型试验研究了张开节理对切缝药包爆生裂纹扩展的影响,指出定向裂纹扩展不会穿过张开节理,而是在节理端部产生翼裂纹;魏晨慧等[4]指出初始应力场的作用不利于裂纹的扩展,节理对裂纹沿节理面方向的扩展具有导向和促进作用;杨仁树等[5]通过模型试验,研究不同炮孔与节理间距下节理处起裂形式,指出节理处起裂有爆生裂纹扩展至节理之前或之后节理处起裂2种形式;赵安平等[6]探讨了节理强度、刚度、间距、倾角对爆破效果的影响,认为在节理岩体中爆破时,爆区内的节理发育程度与爆破效果呈负相关;Wang Y等[7]基于数字激光动态焦散线实验系统,进行了爆炸载荷下垂直开缝PMMA介质中的裂纹扩展实验,指出翼裂纹扩展初始阶段,剪切波起主导作用,膨胀波起次要作用,节理倾角为45°时,翼裂纹扩展长度最长;Yang X等[8]基于爆炸加载实验和AUTODYN软件模拟实验试件的动态裂纹扩展过程,指出充填物类型、角度和距离与反射和吸收的应力波能量存在相互制约的关系。

从上述研究现状来看,国内外学者在岩体中节理的不同几何特征对爆破裂纹扩展影响的研究较少,因此,基于前人的研究,首先探讨和选择爆破破坏理论及数值验证的RHT本构模型,其次利用有限元仿真软件,建立3组不同节理几何特征的岩体准二维模型,对岩体耦合爆破裂纹扩展进行数值模拟。最后研究分析了不同节理宽度、节理长度、节理弯度(弯曲程度)对爆破作用下裂纹扩展的影响规律。

1 岩体爆破破坏理论及数值验证

1.1 岩体爆破破坏理论

根据应力波与爆生气体综合作用破坏理论,结合药包的内部作用可知:炸药在岩体中爆炸后,炮孔周围岩体沿着炸药中心产生不同程度的径向损伤,按照损伤程度依次为粉碎区、裂隙区和振动区。岩石爆破裂纹扩展,其耦合装药粉碎区半径计算公式[9]如下:

(1)

裂隙区半径公式[9]为

(2)

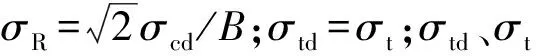
1.2 数值验证

1.2.1 材料模型

1)岩石材料模型。RHT本构模型[10]是由Riedel等提出的一种针对混凝土和岩石等脆性材料的高级损伤模型。它引入弹性极限面、失效面和残余强度面,分别描述材料的初始屈服强度、失效强度及残余强度的变化[11];它包括强度模型和损伤模型,通常与p-a状态方程共同使用,p-a状态方程用来描述多孔隙的脆性材料压力的压缩过程;强度模型主要分为弹性、线性强化、损伤软化3个阶段,3个阶段的表达式[12]如下:

(3)

(4)

σr=Af·(P*)nf

(5)

RHT本构的累积损伤表达式[12]为

(6)

(7)

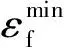
因此,RHT模型可以模拟岩石在动态载荷下的拉伸和压缩损伤演化[13],用于模拟爆破裂纹扩展优势明显[14]。岩体模型材料的参数通过理论计算和参数研究确定[14-15],其部分主要参数如表1所示。

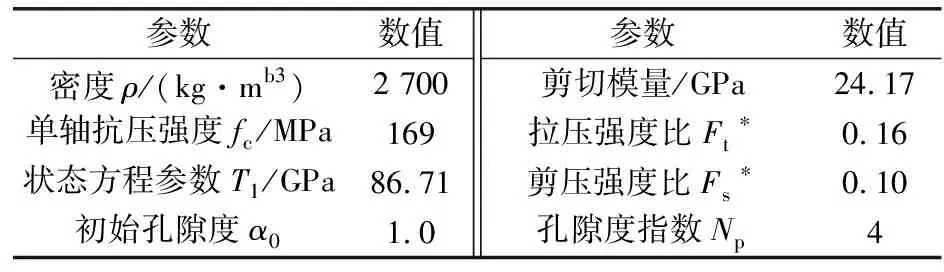
表1 岩体模型参数

2)炸药本构模型及状态方程。炸药选用*MAT_HIGH_EXPLOSIVE_BURN和JWL状态方程来描述,其JWL状态方程表达式为[16]

(8)

式中:P为爆压;V0为初始相对体积;E0为初始内能;A、B为材料常数;R1、R2、ω为状态方程常数。其具体参数如表2所示。

表2 炸药材料及状态方程参数

3)耦合空间(空气)材料模型及状态方程。耦合空间(空气)采用*MAT_NULL材料模型,其状态方程为*EOS_LINEAR_POLYNOMIAL,具体参数如表3所示。

表3 耦合空间(空气)材料及状态方程参数

1.2.2 数值模型

为验证选取的参数、材料模型以及岩体爆破裂纹扩展数值模拟的准确性,利用有限元分析软件,按照所选的材料本构模型及参数,建立数值模型(见图1),对单孔耦合装药爆破裂纹扩展进行模拟。为了简化数值模拟计算、减少模拟结果所占计算机的存储空间,建立一个二分之一、z方向为一个单元格的准二维模型,其中AB长400 cm,AC长200 cm,炮孔直径5 cm,因其研究耦合装药下爆生裂纹扩展规律,则装药直径为5 cm,CD定义为对称边界条件,AB、BD、AC定义为无反射边界条件,约束岩体z轴方向不动。黄佑鹏等[17]指出当耦合空间半径大于炸药半径10倍时,计算结果是正确、收敛的,因此取空气长75 cm、宽为37.5 cm,设置模型网格尺寸大小约为0.5 cm×0.5 cm×0.5 cm,炸药网格单元54个,耦合空间(空气)网格单元11 204个,岩体网格单元319 957个,其网格划分如图2所示。为了避免网格畸变过大,导致产生负体积运算错误,因此有限元模拟采用流固耦合算法,炸药与耦合空间采用ALE算法,岩体采用Lagrange算法。

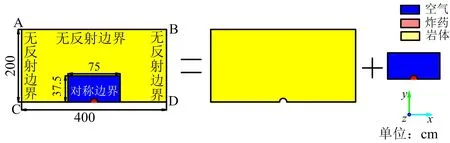
图1 数值计算准二维模型Fig.1 Numerical calculation of quasi-2D model

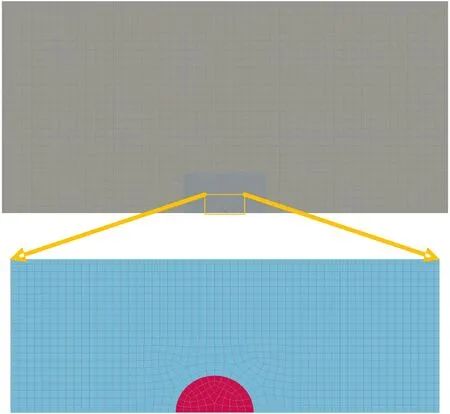
图2 模型网格划分Fig.2 Meshing of model

1.2.3 数值实验验证

在爆破过程中,RHT模型损伤(Damage)云图可以反映岩体损伤情况,岩石未损伤时,Damage=0,岩石完全损伤时,Damage=1[18]。炸药在岩体中爆炸时,炸药爆炸的强烈冲击波与爆生气体作用于炮孔近区岩体,形成爆破空腔,产生粉碎区;随着爆炸冲击波在岩体内继续传播逐渐减弱为应力波,炮孔附近的岩体在爆炸应力波作用下开始产生径向、环向裂纹,远区裂纹呈放射状分布,形成裂隙区,单孔耦合爆破理论结果和数值模拟结果分别如图3和图4所示。

图3 单孔耦合爆破理论结果Fig.3 Theoretical results of single-hole coupled blasting

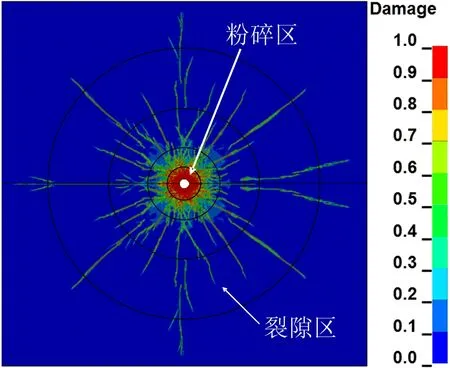
图4 单孔耦合爆破数值结果Fig.4 Numerical results of single-hole coupled blasting

可以看出,理论结果与基于RHT模型的数值模拟结果裂纹扩展模式及损伤分布的一致。通过Ls-propost后处理软件中的measure板块得到粉碎区与裂隙区的半径分别为12.7、167.2 cm。通过式(1)、式(2)及表1、表2理论计算粉碎区与裂隙区半径分别为14.2、165.8 cm,数值模拟获得的粉碎区与裂隙区的半径与理论计算结果基本一致。因此,所采用的RHT模型及相关材料参数适用于研究爆破裂纹扩展模式及岩体的损伤情况,且进一步用于研究节理几何特征对爆破裂纹扩展的影响。

2 数值模拟方案

运用ANSYS/LS-DYNA软件,建立3组不同节理几何特征的数值模型。第1组是不同节理宽度条件下的岩体爆破,节理长度为40 cm,节理距炸药中心60 cm,节理宽度分别为1、2、3、4 cm,对应的模型编号分别为I、II、III、IV,用于考察节理宽度对岩体爆破裂纹扩展的影响。第2组模型是在相同节理宽度(1 cm)及位置(距炸药中心水平位置60 cm)条件下建立节理长度分别为60、80、100 cm的模型,模型编号分别为V、VI、VII。第3组模型是在相同节理宽度(1 cm)及距炸药中心水平位置60 cm条件下,分析节理弯曲程度对爆破裂纹扩展的影响。为了定量确定节理弯度,引用弯度定义,弯度是中弧线离弦线的最大距离与弦长度的比值。采用半径、角度、弯度共同确定节理的形状和位置,半径为圆心到节理的距离,角度为节理端部和圆心的连线与水平方向的夹角。以模型I中的垂直节理(弯度为0)、长度及其距炮孔中心的距离作为参考,建立3种不同弯曲程度的节理:经计算,半径与角度分别为40 cm、57.30°的节理对应的节理弯度为0.128;半径与角度分别为60 cm、38.20°的节理对应的节理弯度为0.084;半径与角度分别为80 cm、28.65°的节理对应的节理弯度为0.063,其模型编号分别为VIII、IX、X,具体弯度、半径及角度如图5所示。以上数值模拟不同几何特征的节理均采用*MAT_PLASTIC_KINEMATIC材料本构模型,其力学参数[19]如表4所示。

图5 不同节理弯度Fig.5 Camber of different joints

表4 节理材料模型参数

3 爆破裂纹扩展数值模拟结果分析

3.1 节理宽度对爆破裂纹扩展的影响

在不同节理宽度对爆破裂纹扩展的影响数值模拟中,选择基于已验证的岩体、炸药本构模型及参数,对含节理宽度1、2、3、4 cm的岩体进行爆破模拟,设置与数值验证相同的边界条件、网格尺寸及求解时间等选项,其数值模拟爆破裂纹扩展结果如图6所示。

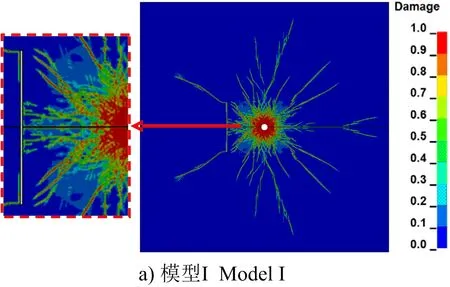
图6 不同节理宽度条件下的爆破裂纹扩展Fig.6 Explosion crack propagation under different joint width conditions

从图6可以看出,对于不同节理宽度的4种模型,粉碎区的半径范围、爆破裂纹扩展形式大致相同,说明节理宽度大小对粉碎区裂纹扩展影响较小;节理端部产生翼裂纹,且翼裂纹先呈水平扩展,后翼裂纹改变扩展路径,这是由于爆炸应力波扩散至节理面时,应力波发生反射、透射与绕射导致节理端部发生应力集中现象,应力强度因子超过岩体断裂韧度使岩体开裂并扩展,形成水平和弧形翼裂纹,且水平翼裂纹长度随着节理宽度的增加递增。

观察图6中炮孔与节理之间岩体裂纹发展情况可以发现,随着节理宽度的增加,朝向节理扩展的裂纹范围逐渐增大,裂纹逐渐变粗变长,此部位岩体损伤越严重。

为分析其原因,在节理中间距炸药中心水平距离30 cm位置处选择参考点E(见图7)。

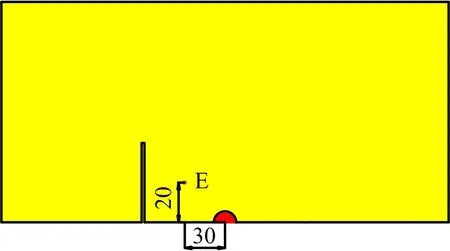
图7 参考点E位置Fig.7 Reference point E position

利用Ls-prepost后处理软件中的history模块获得不同节理宽度条件下E点的有效应力曲线,并提取曲线中的第二峰值应力大小(反射应力波产生的有效应力大小),绘制节理宽度—第二峰值有效应力曲线,结果如图8所示。

图8 不同节理宽度条件下点E的第二峰值有效应力Fig.8 Second peak effective stress at point E under different joint width conditions

从图8可以看出随着节理宽度的增加,参考点E的第二峰值有效应力从85.2 MPa增大到125 MPa,与图6中所示的炮孔与节理之间的岩体裂纹扩展范围及损伤程度的变化趋势一致。通过对比分析可知,随着节理宽度的增加,爆炸应力波通过节理产生的反射拉伸应力越大,阻滞应力波的作用越明显,导致炮孔与节理之间的岩体损伤程度及裂纹范围增大。

3.2 节理长度对爆破裂纹扩展的影响

在相同节理宽度(1 cm)及节理位置(距炮孔中心水平距离60 cm)条件下,对比分析不同节理长度对单孔耦合爆破岩体裂纹扩展的影响。在节理长度分别为40、60、80、100 cm条件下,爆破裂纹扩展及损伤情况如图9所示。

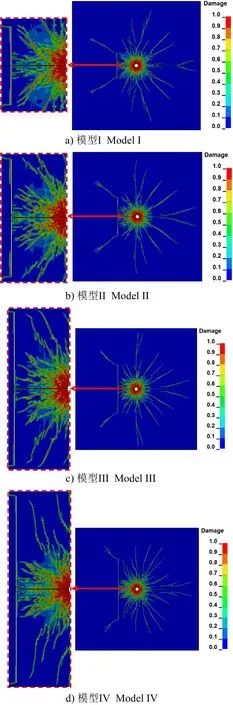
图9 不同节理长度条件下的爆破裂纹扩展Fig.9 Explosion crack propagation under different joint length conditions

从粉碎区范围来看,粉碎区裂纹扩展基本无变化,说明节理长度对粉碎区范围影响也较小;节理长度的递增导致翼裂纹扩展长度逐渐减小,节理与炮孔之间平行于节理的主裂纹长度出现递增趋势。

为分析节理长度对节理与炮孔之间平行于节理的裂纹扩展影响,以模型VII(节理长度100 cm)为选取参考点的基础模型,在节理与炮孔之间中心位置平行于节理自下而上选择等间距(20 cm)的4个参考点E、F、G、H(见图10),绘制各参考点的有效应力时程曲线,结果如图11所示。

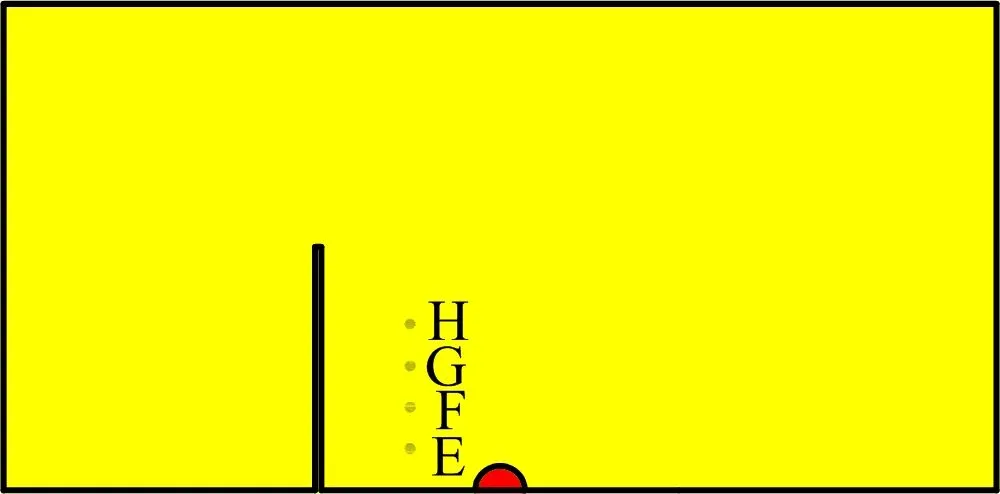
图10 参考点E、F、G、H位置Fig.10 Reference point E, F, G, H position

图11 各参考点有效应力时程Fig.11 Time-history of effective stress at each reference point

由图11可知,在相同节理长度下,随着参考点位置的上移,爆心距的增加,参考点E、F、G、H峰值有效应力逐渐递减,符合经典爆破理论。在相同参考点下,随着节理长度的增加,各个参考点的峰值有效应力增加,说明节理产生的反射拉伸波与爆炸应力波共同作用促进了炮孔与节理之间平行于节理的裂纹扩展。

为进一步分析节理长度对节理端部翼裂纹长度扩展的影响,提取不同节理长度的端部有效应力数据,绘制爆破过程中节理端部的有效应力时程曲线,结果如图12所示。

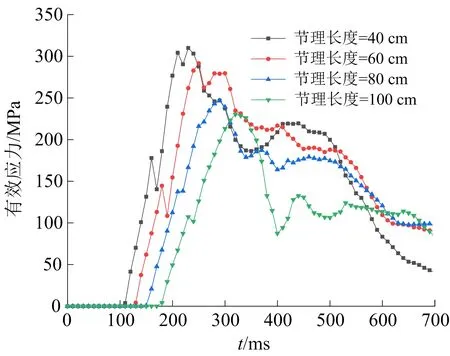
图12 不同节理长度的端部有效应力时程Fig.12 Time-history of effective stress at the ends of different joint lengths

对比分析图11、图12可知,节理端部峰值有效应力明显大于参考点E、F、G、H的峰值有效应力,说明节理的存在导致节理端部发生应力集中现象,且观察图12可知,随着节理长度的增加,节理端部峰值有效应力减小,说明节理长度的增加导致节理端部应力集中现象减弱,翼裂纹扩展长度减小。

3.3 节理弯曲程度对爆破裂纹扩展的影响

在相同节理宽度、长度及位置(距炮孔中心水平距离60 cm)条件下,研究节理弯曲程度对单孔耦合装药爆破裂纹扩展及损伤程度的影响,在弯度0(垂直节理)、0.063、0.084、0.128的节理弯度条件下爆破裂纹扩展及损伤图像如图13所示。

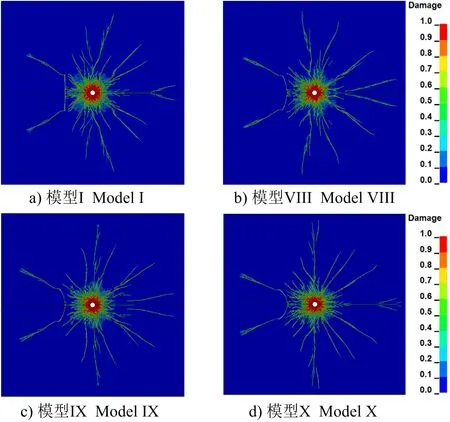
图13 不同节理弯度条件下的爆破裂纹扩展Fig.13 Explosion crack propagation under different joint camber conditions

模拟结果显示,节理弯度的增加对粉碎区裂纹扩展范围及损伤程度影响仍然较小;随着节理弯度的增加,节理左侧弧形翼裂纹弧线逐渐下移,弧形翼裂纹起裂夹角(弧形翼裂纹与水平方向夹角)逐渐减小,爆生主裂纹长度逐渐增大。对4种不同节理弯度条件下,爆破产生的弧形翼裂纹长度、主裂纹长度及弧形翼裂纹起裂夹角进行统计,统计结果如表5、表6所示。

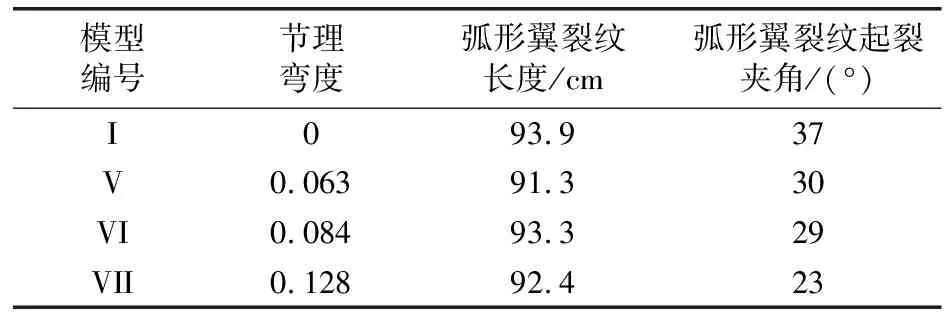
表5 不同节理弯度下弧形翼裂纹扩展长度及起裂夹角

表6 不同节理弯度下主裂纹扩展长度

由表5可知,4种不同节理弯度条件下,弧形翼裂纹长度分别为93.1、91.3、93.3、92.4 cm,弧形翼裂纹起裂夹角分别为37°、30°、29°、23°。可见,不同的节理弯度对爆生翼裂纹扩展长度及起裂夹角有不同影响,且弧形翼裂纹起裂夹角与节理弯度呈负相关。

由表6可知,节理弯度的递增,导致平均主裂纹长度由101.9 cm递增到127.0 cm,岩体破碎范围增大。由此可知,节理弯度的增加对爆破裂纹扩展有促进作用。

3.4 不同节理几何特征对爆破裂纹扩展的影响

节理的存在导致节理端部应力集中,产生翼裂纹;随着节理的几何特征变化,爆破裂纹扩展整体表现出复杂性与差异性,对节理与炮孔之间岩体的裂纹扩展及损伤情况影响较大,对粉碎区范围内裂纹扩展及损伤情况影响差异较小,其原因是节理几何特征的变化导致爆炸应力波的反射、透射和绕射的区域与强弱不同。为进一步分析不同节理几何特征对爆破粉碎区的影响,统计3组不同模型的粉碎区半径数值模拟结果,其结果在12.4～12.9 cm之间,可见,与无节理数值模拟验证粉碎区半径12.7 cm对比,节理的宽度、弯度、长度变化对粉碎区范围内裂纹扩展及损伤情况影响较小。