基于ALO-ELM的隧道超挖预测及其影响因素敏感性分析

2023-11-02吴心怡

工程爆破 2023年5期

陈资,吴心怡

(广东理工学院智能制造学院,广东肇庆 526100)

钻爆法是隧道开挖的最主要施工方法,具有投资成本低、施工工艺简单和对地质条件适用性强等优点,然而该方法会不可避免地造成隧道围岩损伤,无法有效保证隧道轮廓尺寸[1]。作为钻爆法常见的不良影响,隧道超挖不仅会增加施工成本,而且引起支护结构失稳坍塌等安全问题[2],因此,准确合理预测超挖量,优化钻爆法设计参数具有重要意义。

目前,国内外学者对隧道超挖预测研究分为两类,一类是基于统计方法的预测,Hasan Mohammadi等[3]建立了沉积岩隧道爆破超挖的多元线性回归预测模型;陆中玏等[4]分别运用线性Fisher判别模型(FDA)和非线性共轭梯度法(CG)重点分析了地质因素对超挖的影响,但是,该方法无法描述超挖因素之间的非线性和复杂性,导致预测精度低[5]。另一类是基于人工智能算法的预测,李启月等[6]建立基于T-S模型的模糊神经网络地下硐室超挖预测模型;KOOPIALIPOOR M[7]利用遗传算法优化的人工神经网络预测隧道超挖;Adel Mottahedi[8]结合粒子群算法(PSO)和自适应模糊神经网络(ANFIS)对隧道超挖预测进行了研究。极限学习机( ELM)相比于以上算法,具有设置参数少、学习速度快和泛化能力好等优点,能更适用超挖影响因素之间具有复杂非线性关系。另外,影响超挖因素众多,只有通过对因素进行敏感性分析,才能更有针对性地采取措施控制隧道超挖。

综上所述,选取7个影响隧道超挖的重要因素,并用蚁狮优化算法(ALO)对ELM参数进行寻优,解决了传统ELM人工选择参数具有盲目性的问题,提高了模型学习能力和泛化能力,并采用余弦值振幅法开展影响因素敏感性分析,得到影响隧道超挖最重要因素,为控制隧道超挖提供理论指导。

1 隧道超挖影响因素

隧道超挖是指在隧道理论剖面外发生的不必要开挖[9],图1为隧道超挖示意图。影响隧道超挖因素众多,其不仅与爆破参数等可控因素相关,还要受围岩体条件等不可控因素影响,且这些因素之间是复杂的、不确定性的非线性关系。通过结合国内外相关的参考文献,咨询相关专家和现场施工人员的具体意见,分析归纳隧道超挖影响因素如表1所示。

表1 隧道超挖速率影响因素

图1 隧道超挖Fig.1 Overbreak of tunnel

1)爆破参数。炸药单耗PF用作衡量岩石可爆性的尺度,从侧面反映爆破区域岩体特征[10];开挖进尺AL越深,越容易造成钻孔偏角,最终因累积效应导致超挖[11]。间距与荷载比S/B是孔间间距S与排间间距B比值,钻孔率SD是每平方米隧道横截面的孔密度,合理设置S/B和SD能避免炸药的能量造成不必要的岩体破坏[12];此外,段数ND和炮孔深度HD也一定程度影响隧道爆破效果[13]。

2)地质参数。隧道开挖段的地质情况会影响爆破的质量,从而导致开挖时出现超挖。RMR作为一种岩体地质力学分类方法,综合考虑了岩块强度Sc、岩石质量指标RQD、节理间距Ja、节理条件Jo和地下水情况Jw这5个参数,RMR值是将上述参数的评分值相加而得,并按节理分类对其进行修正[4]。RMR岩体分级情况如表2所示。

表2 RMR岩体分级

2 隧道超挖预测模型

2.1 极限学习机ELM

ELM是在单隐层前馈神经网络基础上改进的新型智能学习算法,ELM学习速度快、泛化能力好,对非线性样本数据具有较好适用性,被广泛应用于各种预测、分类和回归问题[14]。

对于输入层神经元个数为n,隐含层的节点个数为L,输出神经元个数为m的ELM结构网络,给定样本训练样本(xj,tj),xj=[xj1,xj2, …,xjn]T为输入向量,期望输出向量tj=[tj1,tj2,…,tjm]T,其中j=1,2, …,N,则期望输出值为

(1)

式中:wi为输入权值矩阵,bi为隐含层神经元阈值,βi为输出权值,g(x)为激活函数。

将(1)式转换成行列式形式:

Hβ=T

(2)

式中:H为隐含层输出矩阵,T为目标期望输出矩阵。

输出权值矩阵β为

β=H+T

(3)

式中:H+为矩阵H的Moore-Penrose广义逆矩阵。

2.2 蚁狮优化算法ALO

ALO算法是一种通过模拟自然界中蚁狮捕食蚂蚁行为的群体智能优化算法[15]。蚁狮在捕猎前会挖出一个漏斗状的陷阱诱捕蚂蚁,一旦随机游走的蚂蚁落入陷阱时,蚁狮向陷阱边缘抛沙以防止蚂蚁逃脱,并迅速将其捕食,随后重新修缮陷阱等待下一次捕猎,ALO基本原理如下:

搜寻食物过程中,蚂蚁随机游走的行为可用数学公式表示为

K(t)=[0,cs(2r(t1)-1),…,cs(2r(tn)-1)]

(4)

(5)

式中:K(t)为蚂蚁随机游走的步数集;cs为计算累加和;n为最大迭代次数;r(t)为随机函数;rand是[0,1]随机数。

为确保蚂蚁在可行区域边界内游走的随机性,需要对蚂蚁位置进行归一化处理:

(6)

同时,蚂蚁的随机游走受到蚁狮陷阱的影响,公式如下所示:

(7)

当蚂蚁落入陷阱时,蚁狮通过向陷阱外抛沙以收缩蚂蚁范围,获取蚂蚁位置。因此,随着迭代次数增加,c与d的值自适应的减小,数学表达式为

(8)

(9)

式中:I为比例系数。

每次迭代后,选择适应度最好的蚁狮作为精英蚁狮,为减小算法陷入局部极值概率,蚂蚁的位置由轮盘赌蚁狮和精英蚁狮共同决定:

(10)

最后,蚂蚁被蚁狮吃掉,蚁狮会随蚂蚁的位置更新自己的位置,表达式为

(11)

式中:f为适应度函数。

2.3 ALO-ELM预测模型

为解决隧道超挖影响因素多,且因素之间非线性、强耦合和高冗余,克服ELM模型易陷入局部最优解的缺点,建立了隧道超挖ALO-ELM预测模型,提高预测结果精度和效率,具体流程如图2所示。

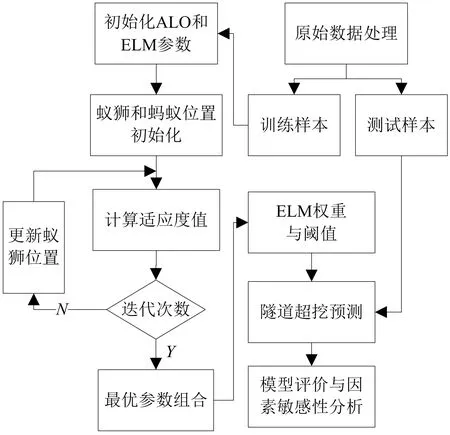
图2 ALO-ELM模型流程Fig.2 The flowchart of ALO-ELM

为了验证ALO-ELM模型的预测性能,引入均方根误差(RMSE)、决定系数(R2)以及方差比(VAF)作为模型评价指标,计算公式如下:

(12)

(13)

(14)

3 实例应用

3.1 数据获取

以广东某高速公路隧道为例,该隧道围岩主要由绿泥石和云母片岩组成,单轴抗压强度约为63 MPa,使用35 mm药筒直径的乳化炸药。选取炸药单耗PF、开挖进尺AL、间距与荷载比S/B、钻孔率SD、延发段数ND、炮孔深度HD和围岩质量指标RMR作为模型输入量,隧道超挖量作为模型输出量,并从该隧道爆破过程中得到50组有效样本数据,具体统计数据如表3所示。

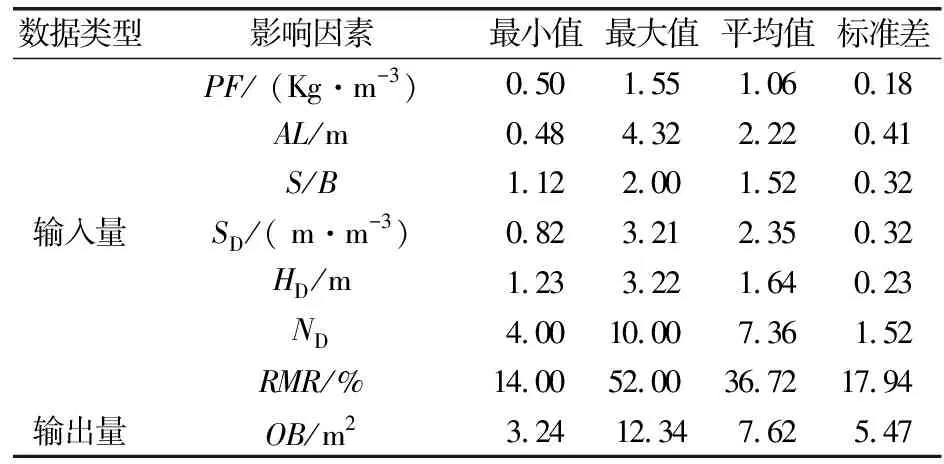
表3 输入量和输出量统计数据

3.2 预测结果与比较分析

选取数据样本前40组(80%)作为预测模型训练样本,后10组(20%)作为预测模型预测样本,经过数据预处理后代入ALO-ELM模型。相关初始化参数设置为:ELM模型中隐含层激励函数为sigmoid函数,输入层神经元个数为1,隐含层的节点个数为6,输出神经元个数为1;ALO算法中种群规模为30,最大迭代次数为100。

为论证该预测模型适用性和优越性,对比分析ALO-LSSVM模型、未优化参数的ELM模型和文献[6]中TS模糊神经网络预测模型的预测结果,对比结果如图3和表4所示。由结果可知,ALO-LSSVM模型平均相对误差5.63%,优于ELM模型的8.59%和PSO-LSSVM模型的11.82%;另外,相对于另2种模型,ALO-LSSVM模型预测值曲线更贴近测量值曲线。

表4 模型预测结果和相对误差

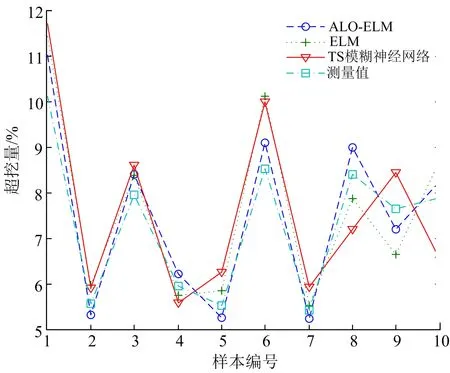
图3 不同模型相对误差对比Fig.3 Comparison with the relative errors of different models

为了进一步评价3种模型的预测性能,引用第三节中RMSE、R2以及VAF作为评判指标,结果如表5所示,其中ALO-LSSVM模型的RMSE为0.48,分别低于ELM模型的0.82和PSO-LSSVM模型的1.00,且94.68%,均明显优于另外2种模型。由此可见,ALO-LSSVM模型的预测结果误差小,精度高,更可靠,更适合作为隧道超挖预测模型。

表5 模型评价指标结果对比

3.3 敏感性分析

采用余弦值振幅法分析各因素对隧道超挖结果的影响程度,对于数组V=[v1,v2,…,vn],此数组中各元素vi是长度为m的矢量vi=[vi1,vi2,…,vim],因此每个数据节点可以看作m维空间中的一点,任意2个数据样本vi和vj之间的影响程度hij可以由式(15)得出,0≤hij≤1,hij越接近于1说明两因素之间关联程度越大。

(15)

敏感性计算结果如图4所示,对比可以看出,各个因素影响程度由高到低排序为钻孔率SD>间距与荷载比S/B>围岩质量指标RMR>开挖进尺AL>炸药单耗PF>炮孔深度HD>段数ND,其中,钻孔率SD和间距与荷载比S/B影响最为显著,而段数ND对结果影响最小。