基于改进HHT的地下洞室爆破地震波信号时频分析
2023-11-02杨钧凯
孙 苗,杨钧凯,吴 立
(1.湖北国土资源职业学院,武汉 430090;2.中国地质大学(武汉)岩土钻掘与防护教育部工程研究中心, 武汉 430074;3.中国地质大学(武汉)工程学院, 武汉 430074)
爆破地震波监测信号表现为瞬时、突变和震荡特征,属于典型的非平稳信号[1]。时频分析已成为处理这类信号的重要手段[2]。常用的时频分析方法[3-5]有:短时傅里叶变换(STFT)、连续小波变换(CWT) 、离散小波变换(DWT)等。上述时频分析方法建立基础均是傅里叶变换,因而不可避免地会受到傅里叶变换分析非平稳信号缺陷的影响,如出现虚假频率和多余分量等。针对这一问题,Huang N E[6]等提出了HHT算法,该算法依据数据本身的特性进行分解,从根本上突破了傅里叶变换的限制。但是实际施工中爆破地震波信号监测环境复杂,导致监测信号不可避免混有噪声,噪声的存在使得EMD产生严重的模态混淆。同时信号存在开始和结束节点,导致绝大多数算法在端点处无法避免会产生端点效应。模态混淆和端点效应都是影响HHT时频分析精度的主要原因,因此为了获得准确的爆破地震波特征参数,必须对传统的HHT算法进行模态混淆抑制和端点处理。
以烟台某地下洞室爆破地震波监测信号为研究对象,通过进行STFT、CWT、DWT、HHT 和改进HHT的爆破地震波监测信号时频对比分析,最终发现改进HHT算法是一种更具自适应的爆破地震波信号处理算法,能有效抑制HHT在处理含噪地震波信号出现的模态混淆和端点发散的现象。改进HHT算法能有效、准确地对爆破地震波监测信号进行时频分析,提取爆破地震波信号蕴含的时频特征参数,为研究爆破振动有害效应提供了重要的依据。
1 多种时频分析方法原理分析
1.1 短时傅里叶变换
短时傅里叶变换(STFT)[7]是在传统傅里叶变换的基础上通过加窗处理,实现可局部反应信号时频域信息,详见式(1)。
F(τ,ω)=STFT{f(t)}=FT{f(t)·w(t-τ)}
(1)
式中:f(t)为原始信号;w(t-τ)是一个以时刻τ为中心的窗函数,其作用是对τ附近的函数做傅里叶变换,得到τ附近的频率信息。
1.2 连续小波变换
将任意L2(R)空间中的原始信号f(t)在小波基函数下展开,称这种展开为f(t)的连续小波变换(CWT)[8],其表达式为
(2)
式中:a为伸缩因子;τ为平移因子;ψa,τ(t)是依赖参数a,τ的小波基函数。
1.3 离散小波变换
连续小波变换中a和τ的变化是连续的,离散小波变换(DWT)[9]是不连续的,DWT定义式为

(3)
1.4 HHT算法
HHT包含两部分,第一部分是Huang N E提出的经验模态分解(EMD);第二部分是Hilbert变换。HHT将时间信号通过EMD得到一组固有模态函数(IMF),再对IMF进行Hilbert变换,得到Hilbert谱,即可描绘出信号的时频谱和幅值谱。
1.4.1 经验模态分解
EMD算法实现过程如图1所示, S(t)为爆破地震波监测信号;Smax(t)和Smin(t) 为上、下包络线;M(t)为Smax(t)和Smin(t)的均值;D(t)为S(t)和M(t)的差值;Ri(t)为余项。
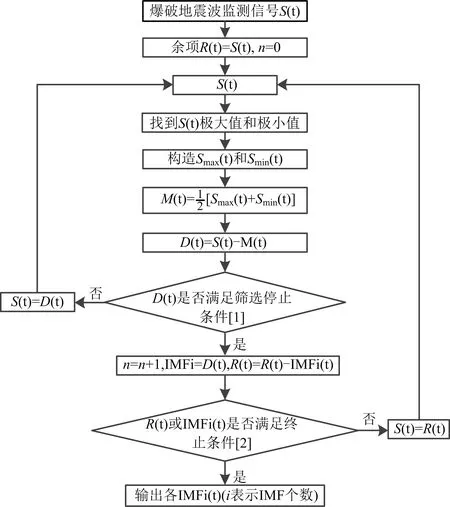
图1 EMD运算流程Fig.1 EMD operation flow
1.4.2 Hilbert变换
Hilbert变换[10]的实质是对任意信号f(t)和h(t)做卷积,将f(t)换成IMF可实现任意IMF的Hilbert变换。
(4)
(5)
1.5 改进HHT算法
1.5.1 EMD模态混淆抑制研究
考虑到爆破地震波监测信号多为含噪信号,噪声的存在导致EMD得到的IMF产生严重的模态混淆,因此解决EMD模态混淆最根本的途径就是对爆破地震波进行降噪处理。
对EMD进行改进得到补充集合经验模态分解(CEEMD)[11],CEEMD是在原始含噪监测信号S(t)中添加2个方向相反的噪声信号,并分别(S1(t)=S(t)+正方向随机噪声,S2(t)=S(t)+反方向随机噪声)进行EMD,即成对呈相反方向增加随机噪声。
CEEMD的具体步骤如下:①成对地添加方向相反的随机噪声到监测信号中,得到S1(t)和S2(t);②对S1(t)和S2(t)分别进行EMD;③重复步骤①、②直到达到预设的添加次数为止;④将步骤②得到的结果进行总体平均。
1.5.2 端点处理
由EMD运算原理可知,IMF产生的原理是不断求均值的过程,均值来自于极大值和极小值包络之差,由于端点不可能同时处于极大值和极小值,导致EMD在端点处发散,这种发散会从端点处向信号中间扩散,数据越短,影响越大。
端点处理最直接的方法就是将原信号端点进行延拓,使得原端点向中间移动,进而使EMD免受端点效应的影响。具体实现如下:
找到信号所有的极大值点的坐标,即(tmax1,xmax1),(tmax2,xmax2)…(tmaxi,xmaxi) (i=1,2,3…M),同理找到信号所有的极小值点的坐标,记为(tmin1,xmin1),(tmin2,xmin2)…(tminj,xminj) (j=1,2,3…N),需要延拓的极大值点和极小值点时刻分别为tmax0和tmin0,其计算分以下2种情况。
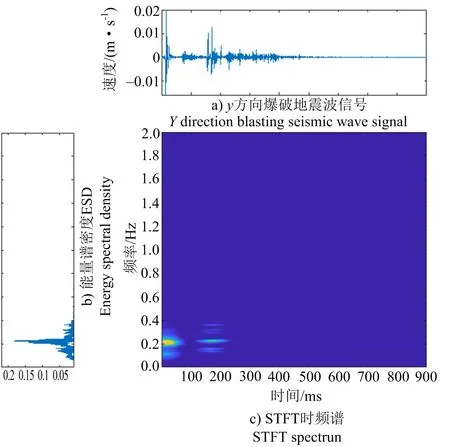
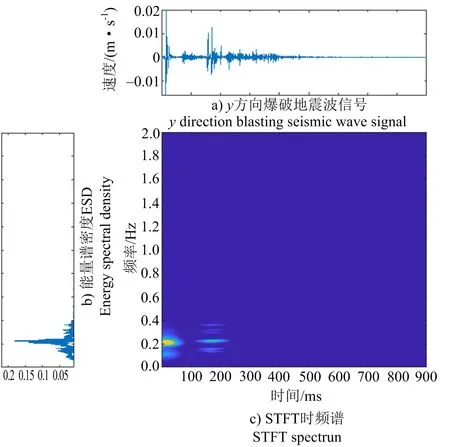
情况1:tmax1 (6) 情况2:tmax1>tmin1,tmax0和tmin0求解见式(7): (7) 对所有极大值点的纵坐标进行多项式拟合,并将计算得到的tmax0代入拟合式,便可计算出xmax0,xmin0的计算和xmax0一致。假设满足情况1,(tmax1,xmax1),(tmin0,xmin0)和(tmax0,xmax0)组成的三角波即为延拓的结果,对此时的信号进行CEEMD即可实现EMD模态混淆和端点抑制处理。对此时得到的IMF进行Hilbert变换即可实现改进HHT爆破地震波信号时频分析。 以烟台某地下水封LPG洞库爆破施工工程为依托,采用TC-4850型爆破测振仪进行监测,选取一条典型的中间主洞室爆破地震波监测信号为研究对象,该地震波监测信号如图2所示。该信号采样频率为4 000 Hz,在0~0.899 s可采集3 600个数据点。 图2 原始爆破地震波监测信号Fig.2 Original blasting seismic wave monitoring signal 采用STFT[Hamming(749)]对图2爆破地震波监测信号进行频谱分析,得到如图3所示的时频谱和能量谱密度图,图3b中的ESD为能量谱密度。从图3可知,当选定了窗函数,即确定了信号的时间分辨率。窗函数越窄,时域特征越明显,在窗内进行快速傅里叶变换会因数据点过少导致快速傅里叶变换精度降低,即频率分辨率降低,导致其在应用过程中只能满足一种分辨率需求。 图3 STFT[Hamming(749)]时频谱和能量谱密度Fig.3 Spectrum and energy spectral density at STFT[Hamming (749)] 对比图3b和图4b可发现,Hamming由749缩小到257,频率分辨率降低,时频谱精度降低,快速傅里叶变换分析结果真实性需要进一步研究。因此STFT适合频率波动不大的平稳信号,不适合爆破地震波这种非平稳、非线性的信号。 图4 STFT[Hamming(257)]时频谱和能量谱密度Fig.4 Spectrum and energy spectral density at STFT[Hamming (257)] 图2爆破地震波监测信号CWT[scale=1:32,db5]处理后,可得到各个小波系数能量占比,如图5b所示,同时得到小波系数在时间-尺度平面上的分布,如图5c所示。观察图5可发现,CWT在分析的过程中虽然可计算出特定尺度-位移平面下的小波系数,但同时也引入了大量的冗余成分,该特点导致小波逆变换重构不唯一。 图5 CWT[scale=1:32,db5]小波谱Fig.5 CWT[scale = 1:32, db5] wavelet spectrum 通过DWT[db5(分解8层)]对图2爆破地震波监测信号进行分解,得到图6所示的结果。观察图6b可发现,信号的高频蕴含在d1~d3中,低频蕴含在d7、d8和a8中,可发现DWT能够较好地描述信号的时频特征,可用于非平稳信号时频分析。 图6 DWT[db5,8层]分量Fig.6 DWT[db5, 8th floor] component diagram 研究发现DWT虽能够在一定程度描述信号的局部特征,但会因小波基选择不同导致不同的分解重构结果,说明小波分量依赖于小波基的选择。图7a是不同小波基函数小波分量d1的对比图,通过该图可发现db5小波基和sym3小波基得到的d1分量之间存在明显的差距,这也从侧面反映,DWT分解并不唯一。进一步观察图6b[db5(分解8层)]得到的小波系数图和图7c[sym3(分解8层)]得到的小波系数图,也可发现明显的差异,因此在小波变换中,小波基函数的选择显得极其重要。 图7 DWT[sym3,8层/db5,8层]小波谱Fig.7 DWT[sym3, 8th floor / db5, 8th floor] wavelet spectrum 针对小波变换受限于小波基选择的问题,采用EMD对图2信号进行分解,得到如图8的分解结果。从图8可见:分量IMF1-IMF2表现为频率高、幅值低、能量低。而即噪声信号一般常表现为高频低能,可初步确定IMF1-IMF2为在实际监测中混入的噪声成分。 图8 实测爆破振动信号EMD结果Fig.8 EMD results of measured blasting vibration signal 不难发现由于噪声的混入,导致IMF4和IMF5在采样点500~700区间内出现了向低频发展的趋势;IMF6在采样点750~1 150区间内出现了向低频发展的趋势,即中高频有向中低频混淆的趋势,这种变化趋势对时频分析的准确性影响很大。 进一步分析发现IMF4、IMF5和IMF6在左端点出现了向低频发散的现象;IMF8和IMF9在信号的左右端点都存在发散现象,端点发散也会对IMF真实性产生不利影响,进而影响HHT时频分析精度。 对图8得到的IMF进行Hilbert变换得到信号的时间-频率-能量谱密度三维图,如图9所示。 图9 基于HHT的时频能量三维图Fig.9 Three dimensional diagram of time-frequency energy based on HHT 图9直观展示了噪声信号以及端点效应对信号整体时频分布的影响,不仅降低了时频分辨率,同时导致实际的时频信息真实性受损,时频分布欠稳定。 通过改进HHT算法求得图2爆破地震波监测信号的时频能量三维图如图10所示。对比图9和图10可发现,通过抑制模态混淆和端点效应得到信号视频能量三维图,在时间和频率上都具有很高的分辨率。本次爆破能量主要集中在150~300 Hz这一频率范围内,这一研究结论和李洪涛[12]关于地下洞室爆破地震波信号频率能量分布研究结果一致。从侧面反映出,改进HHT算法是一种更具自适应的时频分析算法,运算结果具有可靠性,运算更稳定。 图10 基于改进HHT的时频能量三维图Fig.10 Three dimensional diagram of time-frequency energy based on improved HHT 爆破地震波时频分析是为了让爆破科研人员掌握爆破产生的危害效应,并制定对应的爆破危害控制措施[13]。改进HHT算法可实现根据信号本身特征进行解析,同时可实现传统HHT算法模态混淆和端点效应抑制研究,得到高分辨率的时间-频率-能量三维图,实现爆破地震波时频参数提取,有助于爆破危害分析和控制。对爆破振动特性研究和爆破地震波衰减规律学习具有重要的现实意义。 1)STFT窗函数选定,便确定了信号的时间分辨率。因此只适合平稳、线性信号时频分析; 2)CWT中a和τ的变化是连续的,导致计算量大、计算难度大,研究结果引入了大量的冗余成分,导致小波逆变换重构不唯一; 3)DWT中a和τ的变化不连续,能在一定程度描述信号的局部特征,但是过度依赖于小波基的选择,分解不唯一; 4)EMD分解具有唯一性,噪声的存在及端点效应均会影响IMF的稳定性和真实性,导致Hilbert变换后得到的时频分析结果精度不高。改进HHT算法通过抑制模态混淆和端点效应,可得到高分辨率时频分析结果,对爆破振动特性研究和爆破危害控制具有重要的现实意义。2 多种方法爆破地震波信号时频分析对比研究
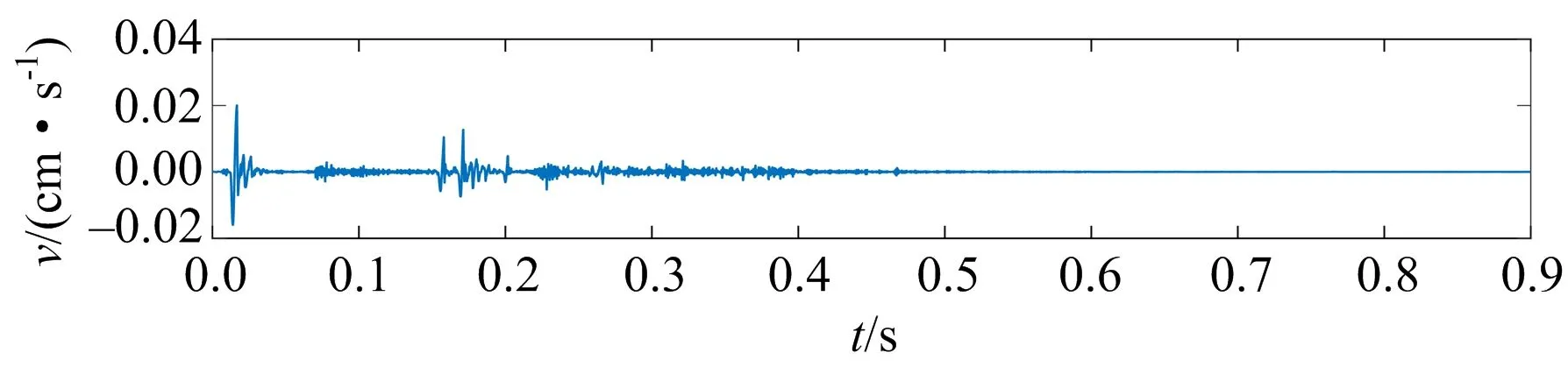
2.1 端点处理爆破地震波信号STFT 时频分析
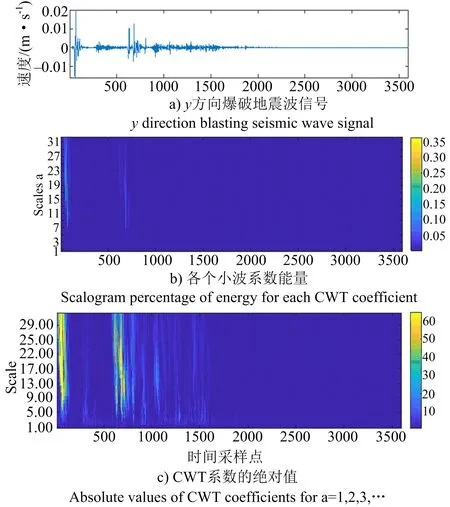
2.2 爆破地震波信号CWT时频分析
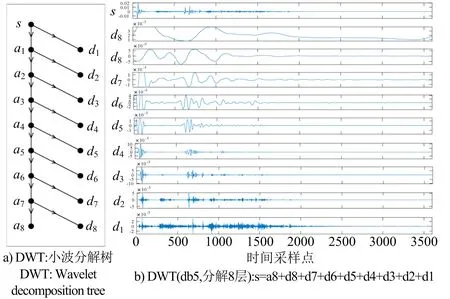
2.3 爆破地震波信号DWT时频分析
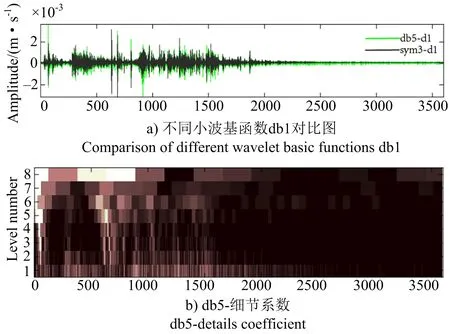
2.4 爆破地震波信号HHT时频分析


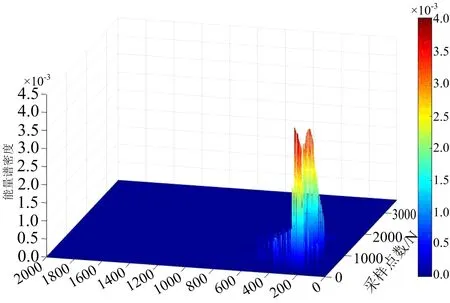
2.5 爆破地震波信号改进HHT时频分析
3 结论
