300 kW航空高速永磁发电机分析与设计

魏嘉麟, 王又珑,3, 温旭辉,3, 陈晨, 李文善

(1.中国科学院电工研究所 中国科学院电力电子与电气驱动重点实验室,北京 100190; 2.中国科学院大学,北京 100049; 3.齐鲁中科电工先进电磁驱动技术研究院,山东 济南 250100)

0 引 言

随着对飞行器节能、减排和降噪要求的日益提高,多电飞机成为未来航空的重要发展趋势,大功率且具有起动发电一体化功能的高速电机系统是其关键技术[1-2]。与此同时,功率密度和可靠性又是航空电机系统的重要指标,因此高速永磁电机是航空系统的最优选择之一[3-4]。

Halbach阵列磁体具有空间磁密谐波含量低、磁路自屏蔽的特点,在无转子铁心的情况下同样能产生较强的气隙磁密,可以提升电机的功率密度[5-6]。环形磁体也可避免间隔导致的护套局部应力增加,从而增加了转子强度[7-8],因此高速Halbach永磁电机在飞行器中获得了越来越多的应用[4]。然而,由于Halbach阵列的特殊排布,磁体内部存在低磁密区域[9-10],并且护套的使用进一步降低了转子散热能力,在涡流损耗的作用下会引起显著的温升[11],增加局部退磁的风险,降低了电机系统的可靠性。因此,航空高速永磁发电机的设计需要在满足多物理场约束的前提下,重点考虑Halbach磁体退磁的抑制技术。

由于计算精度较高、又能够考虑磁饱和等因素,有限元法常用于Halbach磁体的分析[5]。但该方法计算耗时较长,并且受限于网格密度,难以精确计算磁体的局部磁密。解析法计算速度快,能够揭示电机内部的电磁机理,但需要建立精确解析模型对Halbach磁体的低磁密区域进行分析。国内外学者对于Halbach磁体的解析建模已进行了大量的研究,一类使用剩余磁化强度对永磁体建模,列出磁矢位[10,12]或磁标量函数[13-14]的控制方程并求解;另一类则使用磁化电流建模[15]。上述模型多用于分析铁磁材料转子轭,文献[14]所建立的解析模型可以考虑空芯转子的情况。由于Halbach磁体的聚磁性能以及为了增强高速电机的转子结构强度,常选用高强度低磁导率合金材料的实心转子,而现有解析模型难以用于分析。

针对Halbach阵列内部低磁密区域的研究较少,在中低速永磁电机上可以使用增加磁体的充磁方向(如增加45°和60°充磁方向)以及设置磁体之间间隔的方法[9-10]。然而为抑制高速永磁电机的转子涡流损耗,需要对磁体分段处理,轴向长度为毫米级,增加充磁方向会大幅增加制造成本和工艺复杂程度,磁体之间的间隔则会产生较高的护套局部应力。

针对Halbach阵列磁体内部存在低磁密区域和高速电机设计受到多物理场约束的问题,本文建立适用于高强度转子的通用电磁解析模型,与有限元仿真对比来验证模型精度和通用性。使用模型分析磁体低磁密区域的形成机理和影响因素,提出抑制退磁的设计方法。通过场路耦合仿真分别计算两电平和三电平变流器控制下转子的涡流损耗,结合电机温升计算指导磁体的分段设计并选择变流器类型。最后,设计一台装配Halbach磁体的300 kW、30 000 r/min航空高速永磁发电机,制造样机并进行T型三电平变流器控制的发电实验,样机实验和有限元仿真验证模型精度以及设计的有效性。

1 电机基本参数和解析建模

1.1 技术指标与基本设计参数

高速永磁发电机技术指标如表1所示,电机的难度值[16]约为5.2×105。由于碳纤维复合材料抗拉强度较大,并且电导率具有显著的各向异性,垂直于纤维方向电导率很低[17],产生的涡流损耗可以忽略。因此大功率的高速永磁电机更适合选择碳纤维护套[18]。

转速为20 000至40 000 r/min的高速电机常设计为2极或4极。2极电机定子轭部较厚,不利于提高功率密度,并且绕组端部较长,影响转子动力学设计。因此,选择4极24槽方案,额定频率为1 kHz,为降低高频损耗,定子铁心需要使用低损耗软磁材料[19],绕组使用交叉换位的利兹线。由于高速电机损耗密度较高,需要采用定子油冷的方式。

1.2 通用解析模型

高速永磁电机结构图如图1所示,按照材料属性和结构可将高速永磁电机分为转子轭、磁体、护套、气隙和定子铁心几个区域,为了便于建模分析,作如下假设:

图1 高速Halbach永磁电机结构图Fig.1 Schematic diagram of the high-speed Halbach-array permanent magnet machine

1)铁心的磁导率无穷大,忽略磁滞和涡流效应。

2)忽略端部效应,物理量沿轴向无变化,简化为二维分析。

3)不计定子齿槽效应,定子内径为光滑圆面。

4)磁体退磁线及回复线均为直线,忽略磁体涡流效应。

基于以上假设,以轴心为原点建立二维极坐标系进行分析,θ为转子坐标系机械角度,逆时针方向为角度正方向。由于碳纤维材料电磁性能与真空相近,转子护套和气隙同属区域Ⅰ;磁体部分为区域Ⅱ;转子轭部为区域Ⅲ。每段磁体充磁方向如图中箭头所示,Rr、Rm、Rsl和Rs分别为转子轭外径、磁体外径、护套外径和定子铁心内径。

1.2.1 控制方程及其通解

解析模型需要考虑电流的作用,一般选择磁矢位函数A用于求解较为简便。并且,为了便于分析多种充磁方向和排布方式的Halbach阵列磁体,使用磁化强度M表征永磁体剩磁。

区域Ⅰ、Ⅲ的磁矢位函数均满足拉普拉斯方程,磁体区域存在剩磁,磁矢位函数满足泊松方程:

▽2AⅡ=-μ0(▽×M)。

(1)

式中μ0为真空磁导率。在极坐标系下,将永磁体磁化强度沿径向和切向分解为Mr和Mθ。永磁体均匀磁化,因此磁化强度分量与半径无关,只随角度变化。一对极下磁体的磁化强度可用傅里叶级数表示为:

(2)

由于电机结构的周期性,区域Ⅰ、Ⅲ的磁矢位函数的解为:

(3)

(4)

对于4极电机不存在np为1的解。

1.2.2 等效面电流和边界条件

子域模型可以计及定子开槽的影响,然而对于多槽电机求解较为复杂,并且高速永磁电机电磁气隙较宽,齿槽效应相对较弱。因此,本文基于绕组函数理论[20-21]将电枢电流等效为定子内壁的面电流,如下式所示,可通过气隙比磁导函数[13]补偿定子开槽的影响,即

(5)

式中:K为面电流矢量;ωe为电频率;Fkn为k次电流时间谐波、n次空间谐波对应的磁动势,其表达式为

(6)

式中:Np为每相绕组匝数;Ik为k次电流时间谐波幅值;kwn为n次绕组系数,即为分布系数和短距系数的乘积。

根据磁矢位在分界面的衔接条件,边界条件为:

(7)

式中μmr和μyr分别为磁体和转子轭的相对磁导率。对于空载磁密的求解,将面电流密度K设置为0即可。

1.2.3 求解

将各区域磁矢位函数的解析式代入式(7)所示的边界条件,联立方程组即可求解待定系数。为了简化表达式,定义中间变量为:

(8)

(9)

限于篇幅,仅展示空载时区域Ⅰ磁矢位的系数,即

(10)

1.3 模型验证

通用解析模型可用于分析转子轭部为任意磁导率的实心转子,包括铁磁材料、低磁导率和不导磁合金。转子轭部为铁磁材料时,在建模过程中可简化为无穷磁导,因此轭部为非实心时也可使用解析模型分析。以一台采用90°-Halbach阵列高速永磁电机为样机,电机参数如表2所示,选择分布绕组优化反电势波形。分析有铁心和空芯转子两种典型应用,解析计算结果与有限元对比验证模型精度。

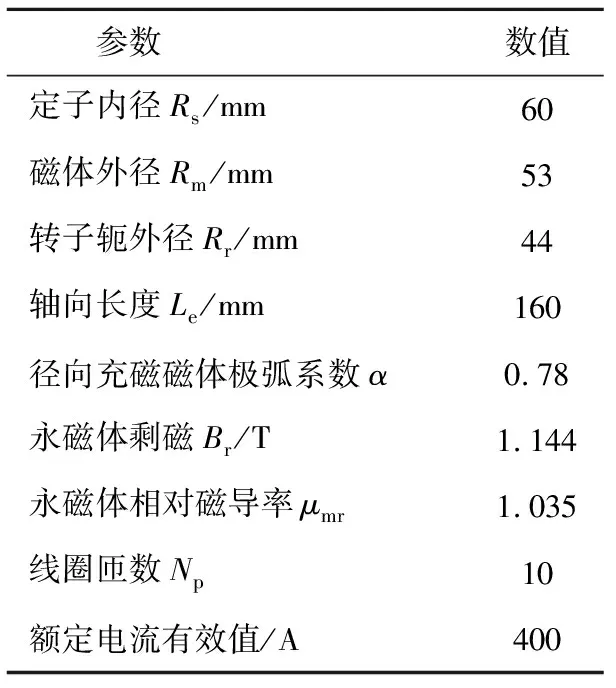
表2 样机参数Table 2 Parameters of prototype

限于篇幅,仅展示磁体内部磁密计算结果的对比,其空载磁密如图2所示。

额定正弦电流激励时磁体内部的电枢反应磁密分布(不包含永磁体产生的磁场)如图3所示。解析解和有限元计算结果非常吻合,验证了模型的精度和通用性。

图3 磁体内部电枢反应磁密Fig.3 Armature reaction magnetic flux density in magnet

2 Halbach磁体退磁分析与优化设计

通用解析模型具有较高精度,因此可用于分析磁体内部低磁密区域,并提出满足约束的改进措施。

2.1 低磁密区域分析

2.1.1 形成机理

相邻不同充磁方向的磁体会相互在局部产生与充磁方向相反的磁场,造成交界面角落处空载磁密较低甚至退磁。多充磁方向的Halbach阵列磁体制作成本较高、安装的工艺复杂,因此90°-Halbach阵列磁体更为广泛使用,本节仍以参数为表2所示的样机为例分析低磁密区域。解析模型通过有限次级数计算所得N极径向充磁磁体内部磁密径向分量的三维分布如图4所示。有铁心和空芯转子均存在低磁密区域,在图中被圈出,最低处与充磁方向相反。切向充磁磁体在径向充磁磁体内部产生的磁场使交界面附近接近气隙一侧磁密增强,接近转子轭一侧磁密减弱。交界面附近的切向充磁磁体在气隙一侧同样存在低磁密区域。

以径向磁密为例分析,图4(a)中的A点为磁密负向极值。使用解析模型计算该点磁密,无论转子轭部磁导率为何值,其计算结果均不收敛,即随着级数次数增加向负无穷发散。由磁密的连续性可知,A点附近的区域径向磁密为负值。

2.1.2 影响因素

切向和径向充磁磁体之间存在间隔时,A点磁密的计算结果可收敛,同时负磁密区域也会减小。模型计算A点磁密与间隔角度的关系如图5所示。

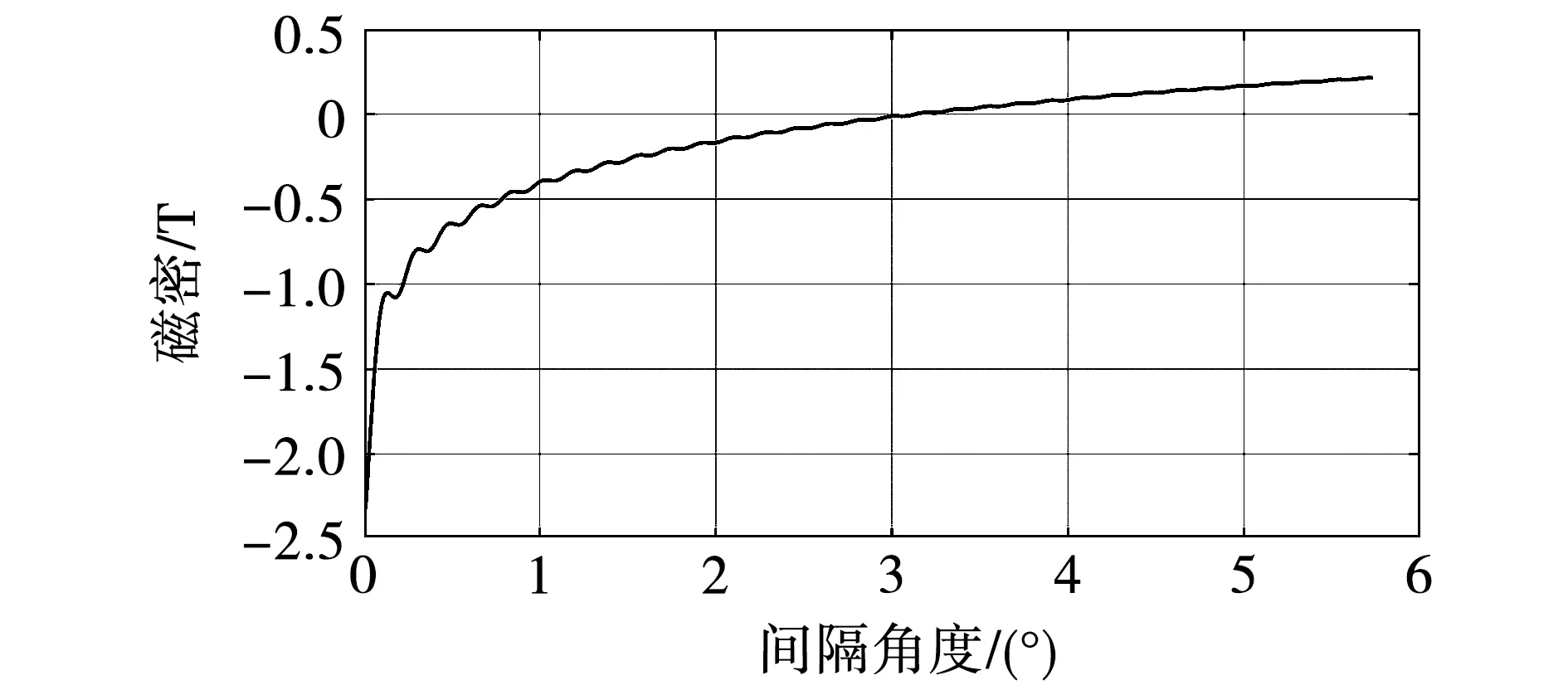
图5 A点空载磁密随间隔角度的变化Fig.5 Radial component of no load magnetic flux at point A vs. gap degree

起初A点磁密随间隔角度的增加而快速上升,然而间隔较大时,切向充磁磁体在A点产生的磁密较弱,继续增大间隔,磁密变化不再明显。间隔3°左右可使A点磁密为正,然而会使护套局部应力显著增大,不利于电机转速和功率的提高。常温下永磁材料线性区较宽,退磁区域较小,但退磁点会随磁体温度升高而上移,使局部产生不可逆退磁。

2.2 电枢反应退磁分析

对于常规永磁电机,常使用额定转速下端部三相短路的特征电流预测磁体退磁情况。然而,Halbach磁体内部的低磁密区域使电枢反应退磁情况变得更为复杂。

使用解析模型分析电枢反应退磁,转子有铁心时电枢反应磁密较强,因此以铁心转子样机为例分析电枢反应退磁。特征电流和发电状态额定电流在低磁密区域产生的电枢反应磁密如图6所示。

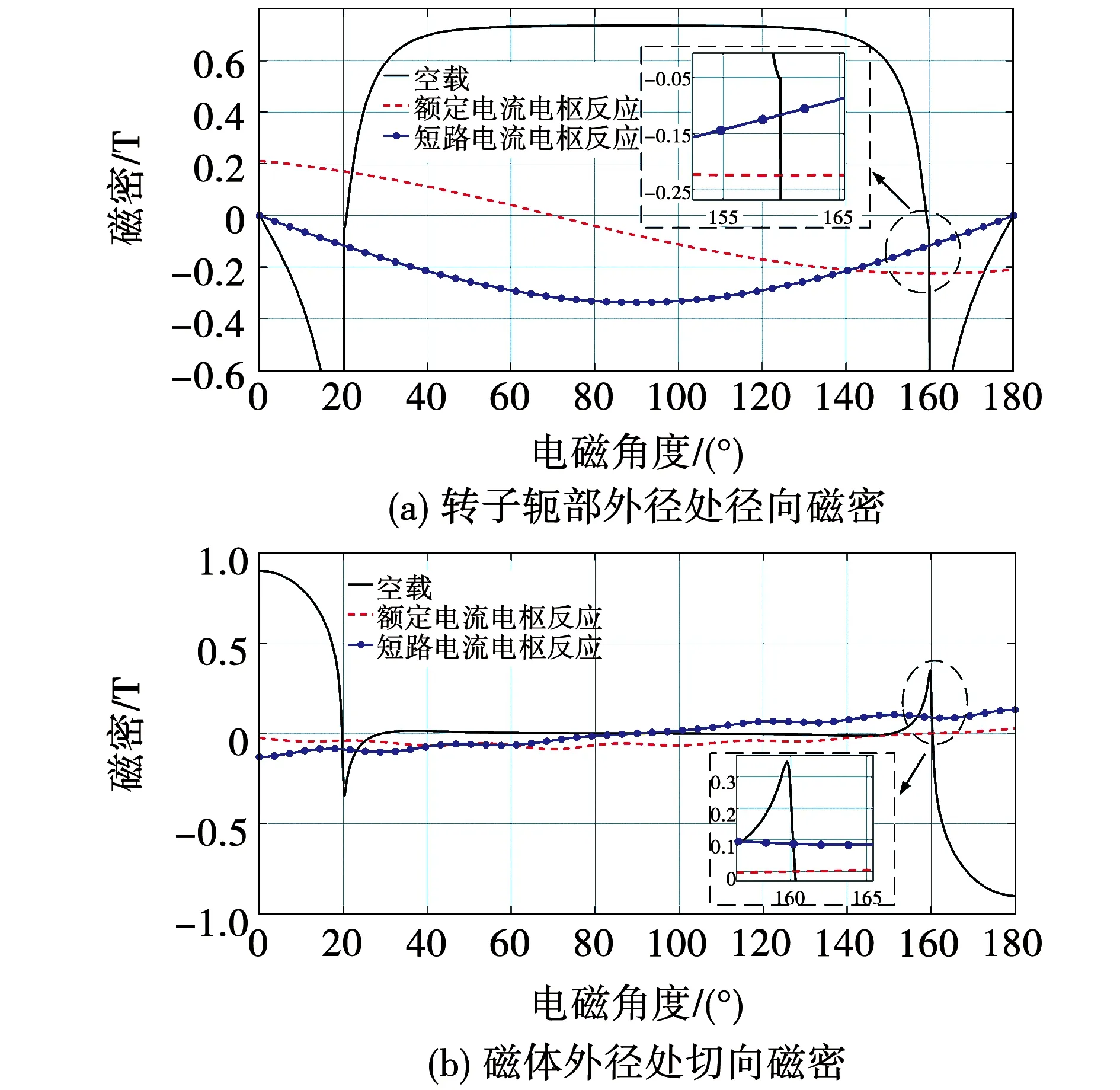
图6 低磁密区域电枢反应磁密Fig.6 Armature reaction magnetic flux density in low flux density parts of the magnet

径向充磁磁体所跨电磁角度为20°至160°时,空载低磁密区域位于其端部附近。根据磁密分布可知,特征电流产生的磁密幅值较大,但负峰值接近于磁体中部,在低磁密区域(160°附近)的负磁密小于额定电流产生的,去磁作用相对较弱。电机运行在电动状态时,额定电流产生磁密的负峰值接近于另一侧低磁密区域(20°附近)。实际应用中,由于系统电压的限制,常需要对高速永磁电机进行弱磁控制,隐极电机弱磁角度较小,容易接近于切向充磁磁体所占的电磁角度(例如10°～20°),此时电枢反应磁密负峰值与低磁密区域重合。因此,额定工况下径向退磁更为严重。

图6(b)为磁体外径Rm附近的电枢反应切向磁密分布,特征电流对切向退磁的作用更为显著,然而,有铁心转子的电枢反应切向磁密相对较小。

使用有限元软件分析样机在额定电流作用下的退磁。由于碳纤维护套耐温有限,转子最高温升应为150 ℃左右,磁体材料选择150 ℃时的N42SH钕铁硼永磁体。图7为磁体内部的径向磁密分布,低磁密区域在额定电流作用下有明显的退磁,多次作用后磁密趋于稳定。

图7 电枢反应退磁Fig.7 Demagnetization caused by armature reaction

2.3 磁体优化设计

由上述分析可知,Halbach阵列磁体在额定工况下容易发生局部退磁,降低电机系统的可靠性。因此需要对其进行抑制,本节以样机为例对磁体进行优化设计。

2.3.1 永磁材料选型与磁体厚度设计

选择永磁材料应考虑工作温度下的退磁拐点对退磁面积的影响。基于线性磁体的通用解析模型计算样机空载退磁面积与退磁拐点关系如图8所示,磁密低于拐点的区域为退磁区域。由图4(a)可知,磁体角落处磁密分布的非线性程度较高,接近A点时磁密急剧降低,因此退磁拐点低于0时退磁面积较小,低于1‰,加工公差导致的间隔可以使退磁面积忽略不计;拐点磁密进一步降低时,退磁面积减小不明显;拐点高于0.1 T时,退磁面积随拐点的上升迅速增加。因此,合理选择材料在工作温度点的退磁拐点能够抑制退磁并控制成本。

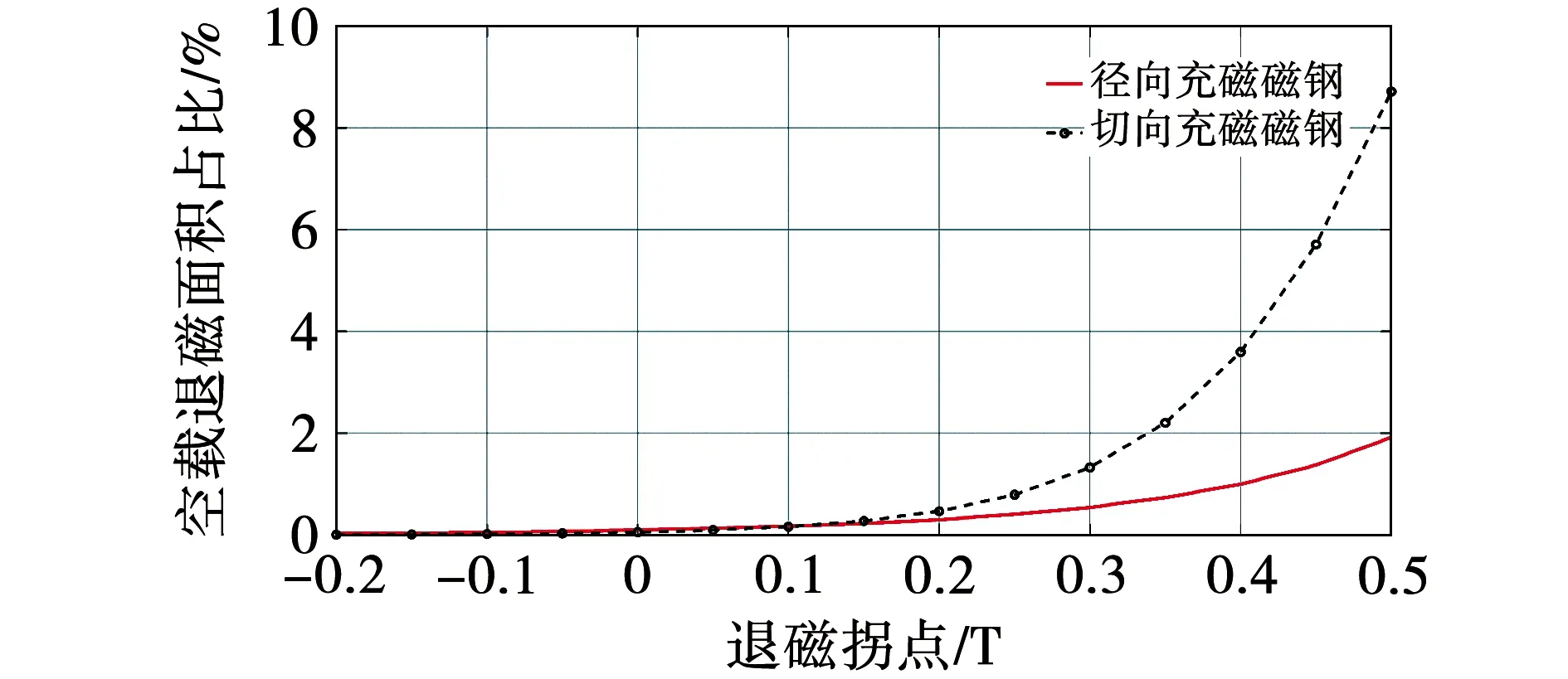
图8 空载退磁面积随退磁拐点的变化Fig.8 Demagnetization area on no load vs. demagnetization value

进而分析电枢反应退磁应计及电枢反应去磁磁密的影响。产生特定的空载气隙磁密(或磁链基波幅值)可以选择不同的磁体厚度,相同的电枢电流作用下磁体越薄则电枢反应去磁磁密越强,因此磁体不能设计得过薄。

2.3.2 分段平行充磁

90°-Halbach磁体只有两种充磁方向的磁体,可调整切向充磁磁体的充磁角度或采用分段平行充磁的方式减小充磁方向突变角度。相邻径向和切向平行充磁磁体充磁方向角度如图9所示,每段磁体所跨角度越大,突变角度越小。

图9 充磁方式Fig.9 Magnetization patterns

当一极下磁体周向均分成9段并为平行充磁时,充磁方向仍然只有两种,气隙磁密基波幅值只增加了约14‰,但径向和切向负磁密面积分别减小为原来的75.8%和22.5%。

2.3.3 有限元验证

将上述方法用于样机磁体的优化:磁体充磁方式为平行充磁,选择钐钴永磁材料。使用有限元模型分析样机在额定电流作用下的退磁,磁体内部径向磁密如图10所示,电枢反应作用前后磁密基本吻合,验证了优化方法的有效性。

图10 退磁抑制方法验证Fig.10 Verification of anti-demagnetization

3 转子损耗抑制和温升计算

高速永磁电机损耗密度远高于常规电机,并且散热条件差,尤其对于内转子电机,难以对转子实施冷却措施。为避免碳纤维护套受热分解和磁体的不可逆退磁,需要抑制转子涡流损耗,并计算电机温升。

3.1 磁体涡流损耗分析

三维有限元能够考虑磁体轴向和周向的分段,因此使用场路耦合有限元法分析变流器和磁体分段对转子损耗的影响。分别分析一极下磁体周向6分段(径向充磁的极弧系数为5/6)和9分段(径向充磁的极弧系数为7/9)的情况,6分段磁体仿真模型如图11所示。

分别由两电平10 kHz、两电平16 kHz和三电平10 kHz的脉宽调制电压供电,在这3种情况下,又分别取永磁体的轴向厚度为5、10、15和20 mm,分析永磁体的涡流损耗,在使用三维有限元软件进行分析计算时,均考虑了涡流的集肤效应。

表3为磁体涡流损耗的计算结果,可以看出,轴向长度为5 mm的分段可显著降低涡流损耗;开关频率为10 kHz的三电平变流器供电下产生的磁体涡流损耗远低于开关频率为16 kHz的两电平变流器产生的损耗,证明了使用三电平变流器供电对磁体涡流损耗抑制的优越性。

进一步地,可计算开关频率为10 kHz的三电平变流器供电下周向9分段磁体的涡流损耗,结果如表4所示。

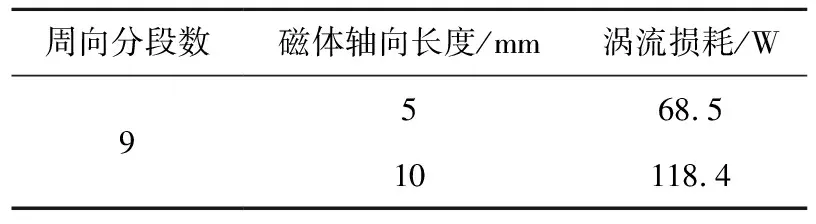
表4 周向9分段磁体涡流损耗计算结果

3.2 电机温升计算

碳纤维复合材料的耐温约为180 ℃,因此额定工况下转子温度应不超过150 ℃。变流器选择载波频率为10 kHz的三电平变流器,使用解析法和场路耦合有限元仿真计算电机损耗。主要包括定子铜耗、定子铁耗、转子涡流损耗和风摩损耗。

由于定子绕组使用利兹线,并且每根导线半径远小于铜材料在额定频率的透入深度,因此可以忽略集肤效应、邻近效应以及环流,使用解析法计算铜耗。根据Bertotti损耗分离模型计算定子铁耗,通过爱泼斯坦方圈法测试铁心材料样件,获得磁滞、涡流和异常损耗系数。使用场路耦合有限元仿真计算三电平变流器供电下的定子铁耗。转子涡流损耗使用周向6分段磁体的有限元计算结果,风摩损耗根据文献[22]所使用的解析法计算。

将各部分损耗值提供至有限元软件计算电机温升,机舱温度较高,因此环境温度设置为80 ℃。定子槽中通入冷却油质,转子最高温度为147.5 ℃,保留了一定的温升裕量。周向9分段磁体产生的涡流损耗略低于6分段磁体,然而制造和工艺成本也会增加,并且根据2.3节分析,6分段磁体所跨角度更大,平行充磁时更利于减小负磁密区域面积。

4 样机与实验

基于以上分析,设计并制造一台300 kW航空高速永磁发电机,额定转速为30 000 r/min,样机及其测试系统如图12所示。

图12 航空高速永磁发电机样机及其测试系统Fig.12 Prototype of aerospace high-speed permanent magnet generator and its test system

转子装配Halbach阵列,为抑制退磁和涡流损耗,一极下磁体周向6分段,径向充磁磁体的极弧系数为5/6,采用平行充磁的方式。磁体厚度设计和材料选择相配合,退磁面积可忽略不计。使用轴向长度为5 mm的分段磁体,并由碳纤维护套缠绕。

使用有限元软件计算转子一阶弯曲模态对应的临界转速高于45 000 r/min,满足转子动力学隔离裕度的要求。测试系统配套T型三电平变流器进行可控整流发电。

4.1 空载实验

对样机进行25 000 r/min空载试验,反电势(electromotive force,EMF)波形的实测、有限元仿真和解析计算结果如图13所示,吻合程度较高,验证了模型精度。线电压基波幅值分别为435、450和460 V,实测电压幅值略低,主要由于端部漏磁和叠片系数的偏差等因素导致。

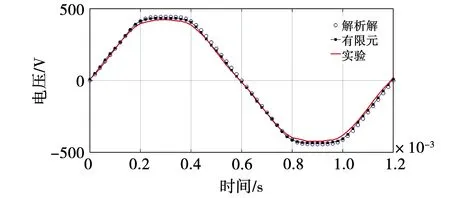
图13 空载反电势波形Fig.13 Measured, simulated and analyzed back EMF waveforms on no load

4.2 负载实验

对样机进行321 kW、30 000 r/min负载实验,电机转矩由高速测扭器测量,发电功率由功率分析仪记录,负载为电阻箱。实验数据如表5所示,电机效率高于96.5%(包括三相动力线的铜损)。

由示波器采集的样机253 kW、25 000 r/min发电实验线电压Uab和两相电流波形如图14所示。为抑制中点电位不平衡,T型三电平变流器使用闭环虚拟矢量调制策略,各级电平无明显偏移,相电流波形较好。

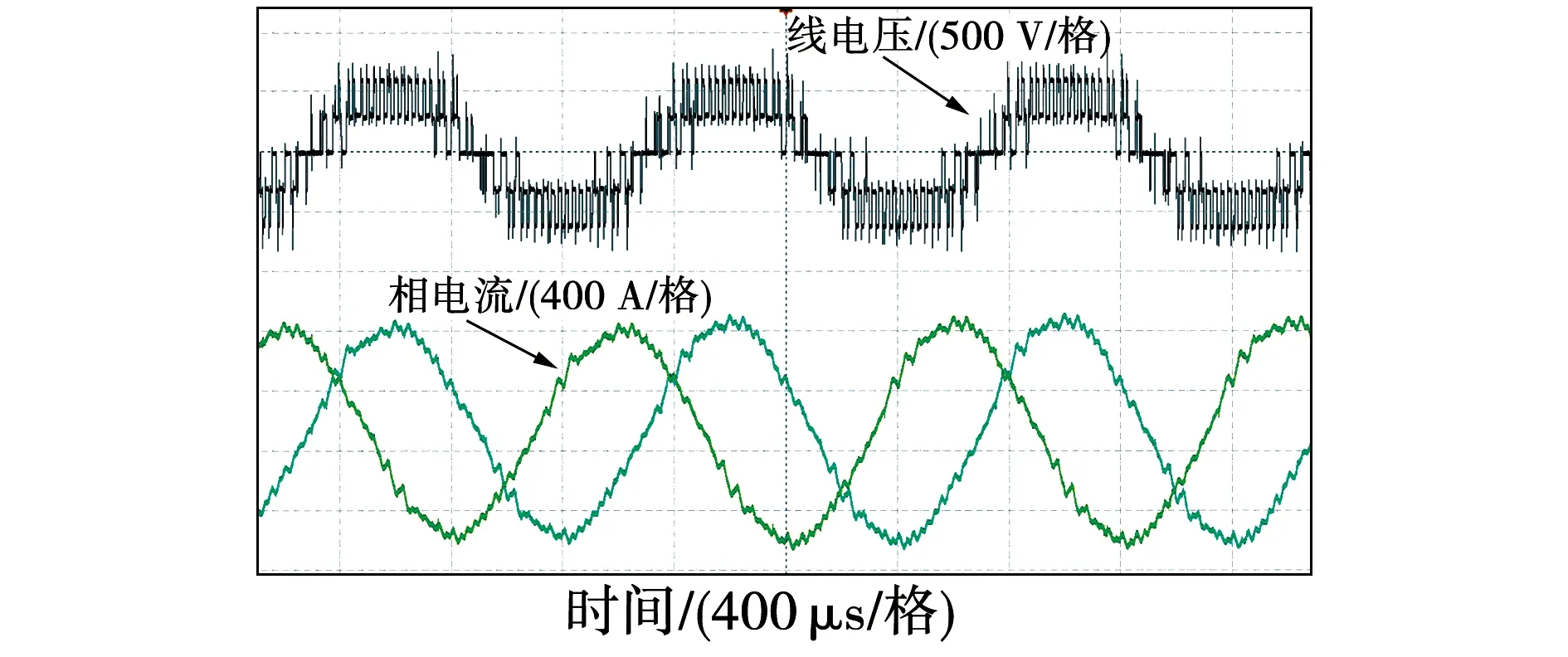
图14 样机25 000 r/min线电压和相电流实验波形Fig.14 Experimental results of the prototype at 25 000 r/min

4.3 磁体优化验证

磁体内部磁密无法实测,因此通过测量电机空载反电势的方法间接验证。样机进行了多次额定功率电动和发电实验前后分别进行空载试验,转速为15 000 r/min。反电势波形对比结果如图15所示,二者基本吻合,不存在因磁体退磁造成的明显衰减,证明磁体无明显退磁。并且,经过一定时长的额定功率实验,转子磁性能和结构完好,未因涡流损耗产生的转子温升造成损坏,验证了磁体优化设计和涡流损耗抑制的有效性。

5 结 论

本文建立了Halbach磁体的通用解析模型,并使用模型分析Halbach磁体内部低磁密区域的形成机理和影响因素,进而优化磁体设计来抑制退磁。使用三维有限元分析磁体的分段方式,抑制磁体涡流损耗。所提出的模型和分析方法用于300 kW、30 000 r/min航空高速永磁发电机的设计,制造样机并进行相关实验,得出如下结论:

1)基于任意磁导率转子轭的电磁解析模型适用于有铁心、空芯转子以及低磁导率实心转子,能够对多种充磁方式的磁体快速建模,与有限元仿真以及样机实验对比验证了模型的精度和通用性。

2)磁体平行充磁可以减小低磁密区域的面积,并且不增加磁体的充磁方向;由于存在低磁密区域,额定工况电枢反应去磁作用强于特征电流。通过有限元模型和样机实验验证,使用解析模型能够合理设计磁体厚度并配合磁体材料(退磁拐点)的选择,可抑制局部退磁。

3)样机实验验证了本文方法对Halbach磁体的退磁和涡流损耗抑制技术的可行性,为Halbach磁体在航空高速永磁发电机中的应用提供了一定的参考。