轮辐式游标永磁电机分析与多目标优化设计

刘洋, 宋宝, 周向东, 唐小琦

(华中科技大学 机械科学与工程学院,湖北 武汉 430074)

0 引 言

受益于磁场调制效应带来的优良转矩特性,近年来游标永磁电机在伺服驱动、新能源发电等领域引起广泛关注。为了提高游标永磁电机转矩密度和转矩品质,研究者们提出了一系列新型拓扑结构,例如“V型内置式”[1]、“轮辐式磁体阵列”[2]、“Halbach式磁体阵列”[3]、“双边调制结构”[4]、“交替极结构”[5]等。

其中,轮辐式游标永磁电机(spoke type vernier permanent-magnet machine,STVPM)不仅可有效减小气隙长度,增加气隙磁导的磁场调制效果,还能充分利用切向励磁结构的聚磁效应,有效提升电机转矩性能。然而,有研究表明由于受其特有磁位波动效应的影响,STVPM的转矩性能提升并未达到预期效果[7]。

针对该问题,研究者提出“交替磁桥”[8]、“双边气隙”[9]等STVPM新型拓扑结构,优化设计了低对极工作磁场的磁通路径,减小和抑制转子磁位波动对电机转矩特性的负面影响。但是,上述方案不可避免导致电机结构更加复杂,大大增加结构变量和设计约束条件,使得该类型电机在高维设计变量空间下的多目标优化设计难度和计算资源需求急剧增加,降低优化设计效率[10-11]。

综上,针对STVPM特有的磁位波动效应,本文以等效磁路模型为基础,推导空载气隙磁密的解析模型,分析该类型电机磁场调制本质特性和磁位波动效应产生机理,研究转子磁位波动对气隙磁场调制效果的作用。进一步地,从电机优化设计方法入手,为削弱磁位波动效应对STVPM转矩特性的影响,解决该类型电机转矩特性综合提升优化设计难度大、效率低的问题,本文提出一种基于参数灵敏度分层的多目标优化设计方法,采用综合灵敏度分析法对设计变量空间进行分层降维,构建具有高精度的电机性能代理模型,运用多目标遗传优化算法对电机转矩密度、齿槽转矩和转矩波动等进行综合优化设计,最终确定优选设计方案,并通过有限元法验算优化设计的有效性和实用性。

1 STVPM磁场解析模型

1.1 等效磁路模型

STVPM的拓扑结构如图1(a)所示,其局部等效磁路模型如图1(b)所示,图中:Zs为定子槽数;Pr为转子极对数;g为气隙长度;hmag为永磁体高度;wmag为永磁体宽度。气隙空间位置θ和转子位置θr间的关系为θr=θ-ωt,ω为转子旋转速度。根据磁场调制工作原理,游标永磁定子绕组的极对数需满足Pa=|Zs-Pr|,本文优先选用Pa=Zs-Pr的组合以充分利用磁场调制效应[12]。

图1 空载等效磁路模型Fig.1 No-load equivalent magnetic circuit model

根据STVPM拓扑结构特征可知,其转子铁心被永磁体分割成相互独立的2Pr块,导致各块转子铁心的磁位相互独立、各不相同。因此,无法参照传统游标电机的磁路计算方法,将转子铁心视为等磁位体,仅分析永磁体磁动势的影响。

为了简化磁场解析计算,假设定转子铁心材料的磁导率为无穷大,忽略饱和效应,可将每块转子铁心的磁位等效成一个节点,进而推导出STVPM的等效磁路模型,如图1(c)所示。图中:Fmag是永磁体磁动势;Λmag为永磁体磁导;Vk是第k块转子铁心的磁位;Λg_k是第k块转子铁心的集总磁导;ψk为第k块转子铁心的磁通量。

1.2 空载磁密特性推导

由于STVPM转子磁路具有不对称性,可归类为双凸极结构电机,其气隙磁导Λ可由下式求解:

Λ(θ,t)≈Λs(θ)Λr(θr)=[Λs0+Λs1cos(Zsθ)]×

[Λr0+Λr1cos(2Prθ-2ωet)]。

(1)

从图1(b)所示STVPM等效磁路模型可获得:

(Vk-Vk+1-Fmag)Λmag+(Vk-Vk-1-Fmag)Λmag+VkΛg_k=0;

(2)

(3)

由于STVPM定子铁心结构的周期性,任意一块转子铁心的磁位Vk应是定转子相对位置的周期函数,且当转子转动一周后其交替变化Zs次。因此,忽略高次谐波项后,Vk可写成式(4)所示形式,将其代入式(2)、式(3)中即可求解出转子铁心磁位Vk:

Vk=(-1)k[V0+V1cos(Zsθ)];

(4)

(5)

(6)

在计算出的每块铁心磁位Vk基础上,利用傅里叶级数展开式求得转子磁动势,如式(7)所示。可见,STVPM转子磁动势分为Fcon和Fadd两部分,其中Fcon与常规游标永磁电机相似,仅与转子永磁体空间位置θr和永磁体极对数Pr有关。Fadd则与定转子的相对空间位置有关,一般称为转子附加磁动势,该分量表征的是由定子开槽对转子磁动势的影响,即为转子磁位波动。

在游标永磁电机一般解析模型中,通常会忽略转子附加磁动势Fadd的影响,仅考虑Fcon作为磁场源对电机的影响。然而,STVPM存在转子磁位波动效应,转子附加磁动势Fadd幅值较大,若忽略其影响,则会带来较大的解析推导误差。并且,需要注意的是,转子附加磁动势的幅值Fa_n为负数,会对气隙工作磁密产生负面影响,即

F(θ,t)=Fcon+Fadd=

Fa1_ncos[(nPr-Zs)θ-nωet]+

Fa2_ncos[(nPr+Zs)θ-nωet]};

(7)

(8)

(9)

(10)

STVPM空载气隙磁密解析表达如式(11)所示,主要包含Pr极对数磁密Bcon、经气隙磁导调制后的调制|Pr±hZs|极对数磁密Bmod。可见,受转子附加磁动势Fadd的影响,空载气隙磁密主要成分与传统游标永磁电机存在较大区别,并且Bcon和Bmod都受到不同程度的削弱,见式(12)～式(16)。特别是在大极比条件下,转子附加磁动势基波Fa_1的幅值更大,此时磁场抑制效果明显,磁位波动效应更加突出,导致转矩性能提升未达到预期效果。

B(θ,t)=F(θ,t)Λ(θ,t)≈

{Bcon_1cos(Prθ-ωet)+

Bmod1_1cos[(Pr-Zs)θ-ωet]+

Bmod2_1cos[(Pr+Zs)θ-ωet]+

Bmod3_1cos[(Pr-2Zs)θ-ωet]+

Bmod4_1cos[(Pr+2Zs)θ-ωet]};

(11)

(12)

(13)

(14)

(15)

(16)

1.3 解析法与有限元对比验证

为了验证推导出的转子磁动势和气隙磁密的解析模型准确性,研究磁位波动效应对电机磁场特性的影响,本文设计了一台12槽14极STVPM电机,其主要设计参数见表1。

STVPM转子磁动势的有限元法与解析法计算结果对比如图2所示。可见,转子磁动势中存在较大的(Zs-Pr)次的分量,即为附加转子磁动势。在考虑转子附加磁动势后,解析法具有较高的精度。

图3为有限元法和解析法计算的STVPM空载气隙磁密的结果对比。可知,当考虑附加磁动势的影响时,气隙磁密解析计算结果与有限元结果基本一致。此外,由于STVPM气隙磁导存在丰富谐波,使得附加磁动势对于不同谐波次数的磁密,影响效果并不完全相同。

2 STVPM多目标优化设计

2.1 优化设计思路

STVPM的参数化结构模型如图4所示,与常规永磁电机相比,该类型电机设计变量较多、参数空间维度较高、磁场调制过程较复杂。在考虑同时满足多个设计目标时,采用经典的单变量扫描法优化所需的计算资源将会急剧增加,并且有可能获得局部最优而非全局最优的方案。

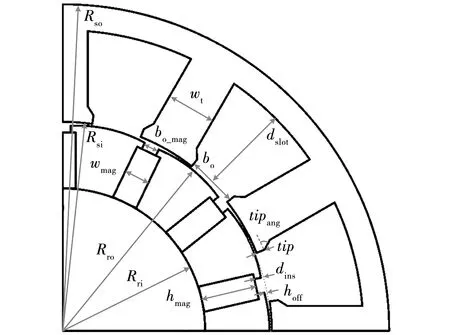
图4 参数化结构模型Fig.4 Parametric structure model

因此,为解决STVPM转矩特性综合提升优化设计难度大、效率低的问题,本文提出一种基于参数灵敏度分层的多目标优化设计技术,通过分析不同设计变量对多个优化目标的影响程度,分别选用针对性的优化设计方法构建电机性能代理模型,然后采用多目标遗传优化算法综合提升电机转矩特性与品质。基于参数灵敏度分层的多目标优化设计流程如图5所示。

图5 多目标优化设计流程图Fig.5 Multi-objective optimization design flow chart

其主要包括以下步骤:

步骤1:根据STVPM设计要求,明确优化目标、目标函数、设计变量和约束边界;

步骤2:运用试验设计法分析所有设计变量对不同优化目标的参数灵敏度,结合综合灵敏度分析法,将初始的高维设计变量空间划分为强敏感层和弱敏感层,实现设计空间的分层与降维;

步骤3:针对强敏感层和弱敏感层变量,分别采用响应面法和参数扫描法进行优化设计;

步骤4:建立不同优化目标下的电机性能代理模型,评估电机性能代理模型的可信度。只有当模型可信度达到要求时,代理模型才可被用于下一步优化设计;

步骤5:基于高可信度的电机性能代理模型,采用多目标遗传优化算法进行设计,根据优化目标函数选择出电机的优选方案,运用有限元计算判断是否达到优化目标。

2.2 优化设计约束

根据STVPM的设计输入要求,确定优化设计的约束条件,主要包括:直流母线电压Vdc=48 V;额定转速nr=3 300 r/min;额定转矩Tr≥0.83 N·m;效率η≥88%;功率因素PF≥0.9;定子外径Rso≤38 mm;气隙长度g≥0.25 mm;槽满率ksg≤0.49;热负荷AJ≤2 400 A/cm×A/mm2。进一步地,选取转矩密度Tdensity、齿槽转矩Tcog和转矩波纹Trip作为优化设计目标,确定优化目标函数f(x)为:

f(x)={maxTdensity(X),minTcog(X),minTrip(X)};

(17)

X=[ksplit,kso,ksd,ktw,krso,tip,tipang,wmag,hmag,dins,hoff,lstk]。

(18)

其中X是为电机的设计变量空间,其初始调整范围见表2。为避免在优化过程中有限元仿真模型出现出现干涉错误,本文选用结构变量比进行参数化建模,具体定义如下:

表2 设计变量及其调整范围Table 2 Design parameters and range

(19)

2.3 综合灵敏度分析

在STVPM优化设计中,由于设计变量繁多,不同设计变量对优化目标的影响程度并不一致,若同时对所有变量进行扫描分析,将会急剧增加优化设计的计算消耗。参数灵敏度可有效地分析和评估设计变量对优化目标的影响强弱,被认为是实现系统和高效优化设计的有效方法之一[13-14]。设计变量x对优化目标y的参数灵敏度S(x,y)定义如下:

(20)

(21)

式中:cov(x,y)为协方差;xm和σx为设计变量x的平均值和标准差;ym和σy为优化目标y的平均值和标准差;N为试验设计的样本空间。

所有设计变量对不同优化目标的灵敏度系数分析结果如图6所示,图中ST、Scog、Srip分别为设计变量对转矩密度Tdensity、齿槽转矩Tcog和转矩波动Trip的灵敏度系数。可见,不同的设计变量对不同优化目标的影响有明显的差异。通常,灵敏度系数越大表明设计变量和优化目标间的内在联系就越强,正灵敏度系数表征优化目标将会随着设计变量值的增加而增大,而负灵敏度系数则表征相反的趋势。

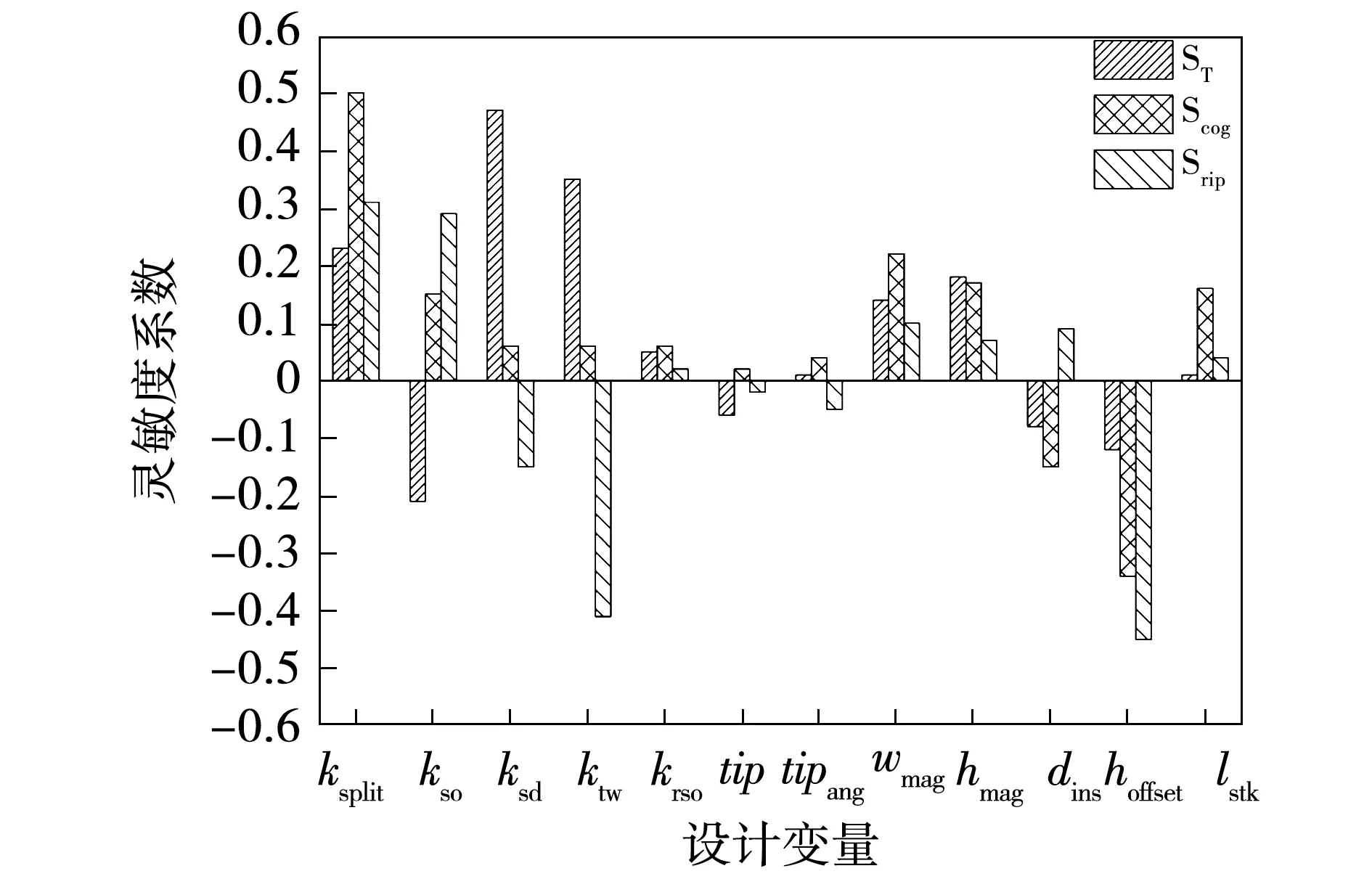
图6 灵敏度分析结果Fig.6 Sensitivity analysis result

由于单个设计变量对不同优化目标的影响程度有差异,仅根据单变量的灵敏度系数进行优化是无法同时满足所有优化目标。本文引入综合灵敏度系数Scom,用于有效评估和确认多目标优化设计问题下变量的敏感程度,其定义如下:

Scom=λT|ST|+λcog|Scog|+λrip|Srip|;

(22)

λT+λcog+λrip=1。

(23)

式中λT、λcog和λrip分别为转矩密度Tdensity、齿槽转矩Tcog和转矩波动Trip的权重系数。考虑到电机设计输入要求,转矩密度Tdensity优先级别高,因此将λT设定为0.6,λcog和λrip设为0.2。最终求出所有设计变量的综合灵敏度系数,见表3。

2.4 代理模型构建与优化

通过比较综合灵敏度系数Scom,所有变量被分成两个不同层次,实现设计空间的分层与降维。表4为设计变量分层结果,针对不同层级的变量,分别选用响应面法和扫描法,建立不同优化目标下的电机性能代理模型。

针对强灵敏度层级的设计变量,选用基于二阶多项式的响应面法,构建设计变量与优化目标的电机性能代理模型,即

(24)

式中:β0、βi、βii和βij是根据试验样本空间数值拟合出的回归系数;ε是随机误差。图7给出了设计变量ksplit和ktw的响应面分析结果。可见,ksplit与ktw对转矩密度Tdensity、齿槽转矩Tcog和转矩波纹Trip的影响趋势和强弱程度并不相同,并且二者之间存在耦合作用互相影响,共同决定了设计目标的最优分布。

通过决定系数Cod评估电机性能代理模型的拟合精度,数值越接近于1,意味着代理模型的精度更加接近有限元模型,表征基于代理模型的优化结果越可信[15]。决定系数Cod定义为

(25)

表5 优化结果Table 5 Optimization results

图8 优化解集和帕累托前沿Fig.8 Optimal solution set and Pareto front

3 电磁性能验证

为了验证所提出基于参数灵敏度分层的多目标优化设计技术的有效性,本文采用限元法分析优化前后的STVPM电磁性能。图9为优化前后在额定转速下电机空载反电势对比图,可以明显看出,优化后的空载反电势波形更加正弦,THDv由优化前的13.1%降至优化后的5.2%,有利于降低电机运行时的损耗和振动。

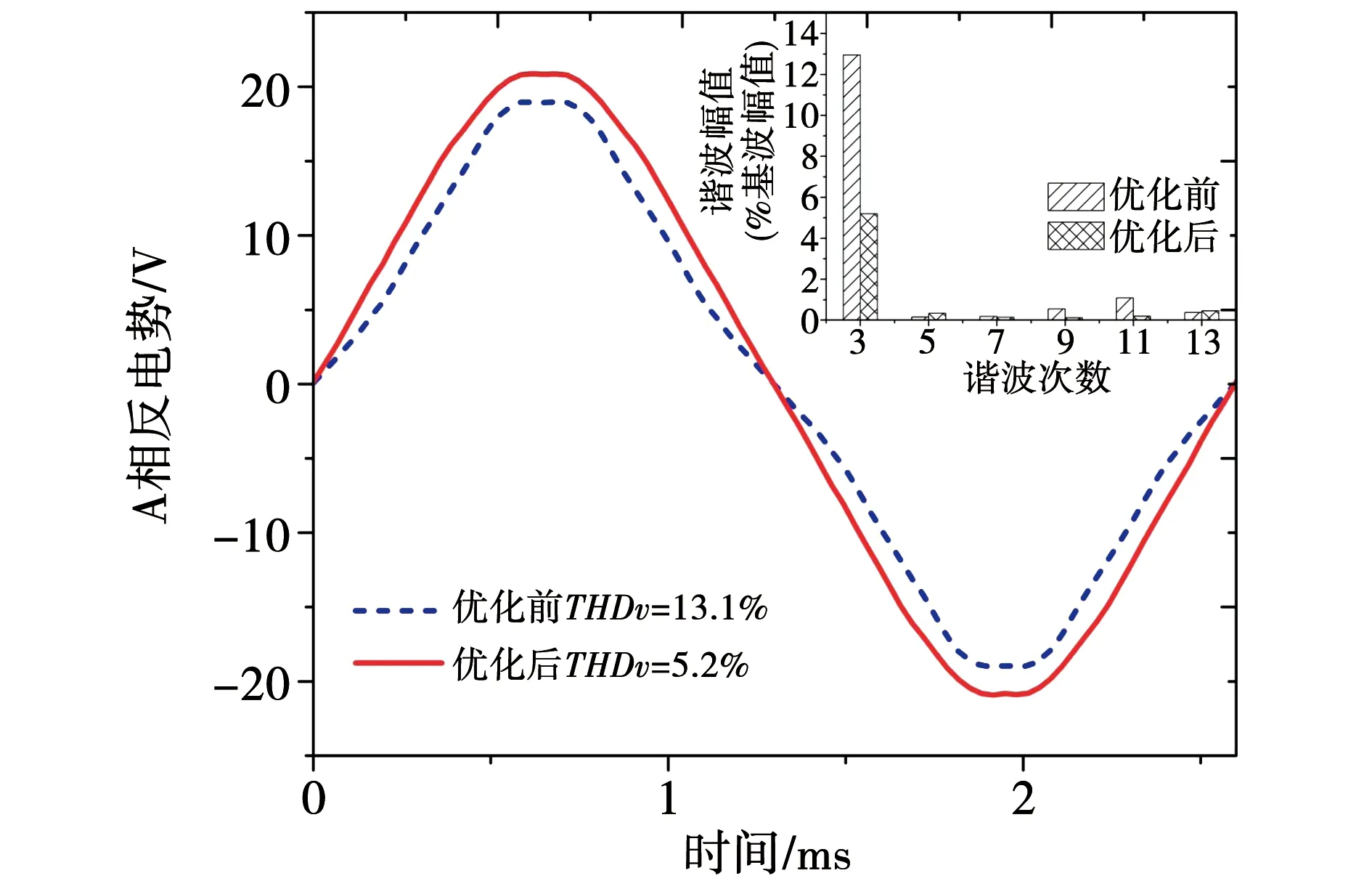
图9 优化前后空载反电势对比Fig.9 Comparison of no-load back EMF before and after optimization

图10为优化前后的电机转矩性能对比结果。可见,优化后电机转矩质量明显提升,齿槽转矩由28.5 mN·m降至10.3 mN·m,转矩波动由4.9%降至1.6%。转矩品质的提高并没有以牺牲输出转矩为代价的,优化后的电机平均电磁转矩从0.68 N·m提升至0.83 N·m。

考虑到STVPM转子铁心的安装工艺,须校核1.2nr转速下转子强度,结果如图11所示。转子最大应力集中于转子极靴顶端和安装齿根部,最大应力约16 MPa,但远低于转子铁心材料和铝合金支架材料的屈服强度,表明优化后电机转子结构强度满足要求。

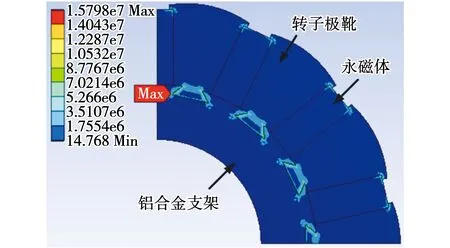
图11 转子强度校核结果Fig.11 Rotor strength calibration results

4 结 论

本文采用解析法分析轮辐式游标永磁电机的磁位波动效应产生机理,建立STVPM的附加转子磁动势和空载气隙磁密解析表达,并采用有限元法进行对比验证,证明解析模型的准确性。为削弱转子磁位波动对STVPM转矩特性的影响,提高多目标优化设计效率,本文提出一种基于参数灵敏度分层的多目标优化设计方法,以综合提升电机转矩密度、齿槽转矩和转矩波动等转矩性能为优化目标,获得优先结构方案。经有限元校核,优化设计后电机空载反电势波形更加正弦,THDv由13.1%降至5.2%。电机转矩特性具有明显改善,齿槽转矩由优化前28.5 mN·m降至优化后10.3 mN·m,转矩波动由4.9%降至1.6%,平均转矩由0.68 N·m提升至0.83 N·m。