基于物理信息神经网络的飞机气动参数辨识方法

付军泉，钟伯文，*，钟运琴，刘 赟

(1.南昌航空大学 飞行器工程学院，南昌 330063；2.江西省飞行器设计与气动仿真重点实验室，南昌 330063；3.中国科学院大学 中国科学院大数据挖掘与知识管理重点实验室，北京 100190)

0 引言

在飞机设计与研制过程中，建立精确的飞行动力学模型是飞行控制系统设计、飞行品质评估、实物及半实物飞行仿真的基础与前提。飞机气动参数一般可通过计算流体力学[1]、风洞试验[2]、参数辨识[3]等方法获得。计算流体力学方法由于存在N-S 方程离散误差、计算截断误差、湍流模型误差等因素，导致精确的飞行流场很难求解。风洞试验中由于存在洞壁效应、相似性效应、传感器测量误差等因素，也使得精确的气动参数获取存在困难。随着传感器技术与飞行试验技术迅速发展，通过飞机气动参数辨识方法、基于飞行试验数据来获取更高精度的气动参数成为一种可行的、必要的手段。飞机气动参数辨识是一个系统工程，主要包括飞行试验设计、飞行动力学模型结构假设、飞机气动参数辨识、模型辨识结果验证四个步骤。

1920 年，Waener 和Norton 对飞行器的气动参数辨识方法进行了早期研究[4]。1951 年，Harry[5]提出了一种以飞机小扰动线性化模型为基础，基于最小二乘法辨识飞机稳定导数与操纵导数的方法。目前，应用最广泛的飞机气动参数辨识方法是极大似然法与牛顿拉夫逊迭代的组合方法。基于极大似然估计的模型参数辨识问题本质上是参数优化问题，但该方法是一种收敛缓慢的算法。Lin 等[6]通过改进极大似然估计方法的参数化梯度的递推中间计算过程，提高了极大似然方法的收敛速度。Kalman 滤波算法能将参数估计问题转化为状态估计问题，依据飞行器的实际飞行情况，采用连续估计模型，并通过离散时间测量与离散滤波算法达到实时估计，其中应用最广泛的非线性气动参数辨识方法是扩展Kalman 滤波（extended Kalman filter,EKF）方法。此外，无迹卡尔曼滤波（unscented Kalman filter,UKF）方法能降低模型线性化所带来的误差，因此在辨识非线性气动模型时有较明显的优势[7]。极大似然法是目前应用于飞机气动参数辨识的主要算法。极大似然法辨识需要给出合理的飞行动力学模型结构以及待辨识参数初始值，不准确的动力学模型会导致气动数据拟合结果不理想，不合理的待辨识参数初始值则容易导致优化陷入局部最小值，甚至导致辨识过程发散[8]。

近年来，人工智能技术的日益成熟为飞机气动参数辨识提供了一种新方法。神经网络可以逼近任何非线性输入输出系统，是一种系统辨识建模的有效工具[9]。基于神经网络的系统辨识可以避免飞行动力学建模过程，并且在气动参数辨识过程中不需要给出待辨识参数的初始值估计。21 世纪初期开始，国内外学者均开展了传统神经网络在飞机气动参数辨识的应用研究，这类方法用神经网络模拟飞行动力学系统的输入输出关系，并利用增量法、导数法从神经网络间接地提取气动参数，是一种数据驱动的辨识建模方法。Ghosh 等[10]基于真实飞行数据建立舵面控制输入与气动力、力矩之间的前馈神经网络模型，并研究舵面控制输入叠加微小增量后的神经网络输出变化，通过增量法提取气动参数。Kuttieri 等[11]研究了基于前馈神经网络的弹性体飞机的气动参数辨识，在建立升降舵、飞行状态输入与升力、俯仰力矩输出之间神经网络模型的基础上，利用深度学习框架自带的微分求导功能，直接求解升力、俯仰力矩输出相对于升降舵、飞行状态输入的导数，得到气动参数。2020 年，Verma 等[12]基于极限学习机器（extreme learning machine,ELM），一种改进的前馈神经网络，并利用导数法辨识基于真实飞行数据的飞机气动参数，结果显示，该方法能显著加速气动力、力矩的神经网络模型的训练过程。

随着深度学习理论与技术的持续发展，2017 年美国布朗大学Raissi 等[13]综合并改进了前人在神经网络求解微分方程方面的技术方法，正式提出了基于物理信息的神经网络（physics informed neural network,PINN）算法框架，并首次提出PINN 方法不仅可以求解微分方程正问题（即建模问题），也可用于求解微分方程逆问题（即参数辨识问题）。PINN 是一种数据与物理双驱动的建模框架，可以将物理约束作为正则项加入到传统神经网络建模过程中，从而减少对建模数据的需求。同时，PINN 相对于传统神经网络，也具有更高的辨识精度[14]。PINN 被正式提出后，引发了流体力学、热力学、生物医学、材料力学等领域大量的相关应用研究[15]。比较典型的网络结构有应用于不可压N-S 方程的分数阶fPINNs 网络[16]，应用于心房颤动诊断分布型DPINNs 网络[17]，应用于新材料设计的贝叶斯型B-PINNs 网络[18]等。基于PINN 网络的系统辨识方法应用研究目前尚不多见。本文研究的重点是根据待辨识动力学系统的特征，设置PINN网络的结构和损失函数。

文章首先给出通用PINN 网络的基本结构以及工作原理，然后给出基于PINN 网络的飞机纵向状态空间模型的气动参数辨识建模方法，最后利用基于JSBSim 的飞行仿真数据验证上述建模方法的正确性与有效性。

1 PINN

设含参数的偏微分方程的通用形式为：

方程的初始条件和边界条件定义为：

其中：空间变量x∈Rd；t为时间变量；Ω为 欧式空间Rd的子集；∂Ω 为 Ω 的边界；微分方程f包含微分算子∂xu、∂tu；λ=[λ1,λ2,...]为 微分方程f的参数；u(x,t)为偏微分方程f的理论解；g(x)为f的 初始条件；h(x)为f的狄利克雷边界条件、黎曼边界条件或混合边界条件。

PINN 用一个神经网络逼近偏微分方程的解。不妨定义PINN 网 络(x,t)逼近微分方程f的解u(x,t)，该PINN 网络的损失函数L定义为：

其中：LPDE为 损失函数中模型驱动的部分；LIC为损失函数中初始条件驱动的部分；LBC为损失函数中边界条件驱动的部分；LData为损失函数中其他数据驱动的部分。损失函数各部分定义如下：

在损失函数（4）的约束下，在尽可能满足偏微分方程的条件下，使PINN 网络的训练数据的误差尽量小。含参数的偏微分方程（1）对应的PINN 网络结构如图1 所示，在输入时间t和 空间x数据后，首先用全连接神经网络(x,t)逼 近函数u(x,t)，然后利用神经网络自动微分技术[19]，求出偏微分方程残差、初值、边值残差，并将其作为正则项加入损失函数中，最后利用梯度下降法更新神经网络权重参数和偏微分方程物理参数。需要说明的是，PINN 广义上是一种基于物理信息神经网络的框架，主要用于求解偏微分方程，但也适用于常微分方程的求解。

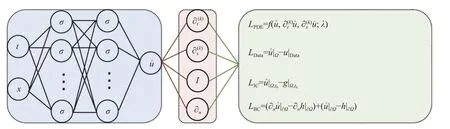
图1 PINN 网络结构示意图Fig.1 Schematic of PINN

2 PINN 气动参数辨识方法

以飞机纵向运动为例，研究基于PINN 网络的飞机气动参数辨识方法。假设飞机在定常平飞状态只受到升降舵激励输入扰动，飞机的纵向运动与横航向运动在该小扰动作用下可以完全解耦，则典型的飞机纵向运动小扰动线性化状态方程可表示为[20]：

其中：u为 流向速度；w为垂向速度；q为俯仰角速率；θ为俯仰角；δe为升降舵偏转角。如无特殊说明，文中所有与飞机飞行状态相关的参数，如u、w、q、θ、δe等，均为扰动增量。进一步假设在上述飞机纵向激励输入下，观测变量与状态变量完全一致，则此处观测方程可略去。

本文飞机气动参数辨识方法研究采用离散型PINN 网络。参考Raissi 等[14]提出的PINN 求解离散型偏微分方程逆问题的方法，构造离散型PINN 系统辨识网络一般需要采用高阶Runge-Kutta 算法离散偏微分方程。本文采用三阶Runge-Kutta 公式离散飞机纵向小扰动线性化状态方程模型。记一阶微分方程通用形式为=f(t,y)，其三阶Runge-Kutta 公式为：

为后文表述方便，将飞机纵向运动小扰动线性化状态方程（9）中与速度u、速度w、俯仰角速率q相关的微分方程分别记为fu、fw、fq：

按式（10）三阶Runge-Kutta 公式将微分方程fu、fw、fq依 次离散化，得到关于u、w、q的递推公式：

由飞机纵向小扰动线性化状态方程的离散化公式（17～19），需要构造PINN 网络，其输入为uk、wk、qk、θk、δek，输出为uk+1、wk+1、qk+1。基于PINN 的飞机气动参数辨识全连接神经网络结构参数见表1，该神经网络共有9 层，激活函数均采用Relu。

表1 PINN 气动参数辨识网络结构参数Table 1 Structure parameters of PINN for aerodynamic parameter identification

PINN 气动参数辨识网络结构如图2 所示。输入uk、wk、qk、θk、δek后，首先用PINN 全连接神经网络预测输出，预测输出与真实输出的残差LData构成数据驱动的损失函数，然后将飞机纵向小扰动线性化状态方程的离散化公式（17～19）中计算输出与预测输出的残差LODE-u、LODE-w、LODE-q作为模型驱动的部分加入损失函数中，最后利用梯度下降法更新PINN 全连接网络权重参数和状态方程中的待辨识气动参数。

图2 PINN 气动参数辨识网络结构示意图Fig.2 Schematic of PINN for aerodynamic parameter identification

3 飞行仿真

研究采用的飞行仿真数据基于JSBSim 求解器产生。JSBSim 是一个可在多种操作系统下编译和运行的开源飞行动力学模型库。JSBSim 既可以作为一个独立的程序运行，从xml 格式的脚本文件和配置文件中获取输入，也可以集成到一个支持交互输入的飞行模拟平台中[21]，如FlightGear 和OpenEaagles。

飞机气动参数辨识需要在飞机配平状态下施加合理的舵面控制输入，以充分激励出飞行动力学响应过程。目前基于时域的气动参数辨识常用的激励输入信号为倍脉冲信号与3211 信号[22]。图3 所示为采用的PINN 网络纵向气动参数辨识升降舵含噪声倍脉冲激励信号与3211 激励信号。倍脉冲激励信号可近似为单位周期内的正弦信号，通过对倍脉冲激励信号宽度的选择，可以将激励所覆盖的频段移至飞行仿真所需要激发的模态频段。同理，在3211 激励信号中，通常将脉冲“2”的宽度设为飞机固有模态频率一半所对应的时间，脉冲“3”与“1”分别设置在飞机固有模态频率的两侧，以形成频带更宽的激励输入。

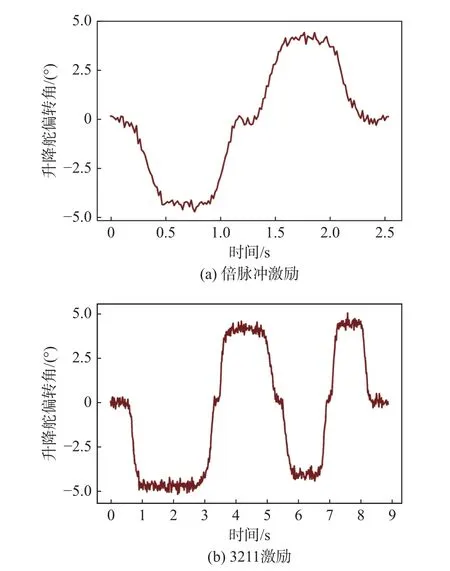
图3 升降舵倍脉冲信号与3211 激励信号Fig.3 Doublet and 3211 activation signal of the elevator

在默认设置下，JSBSim 输出的飞行动力学响应数据是无噪声的，因为JSBSim 会将激励输入信号送入一个低通滤波器滤波，再迭代求解飞行动力学方程。本文主要研究基于无噪声飞行仿真数据的PINN网络纵向气动参数方法，同时为了研究该PINN 网络辨识方法的泛化性，也研究了该方法在含噪声的飞行仿真数据上的辨识效果。含噪声的飞行仿真数据u′(t)定义如下：

其中：u(t) 为原始信号；β ∈(0,1)表 示噪声水平；σ为原始信号u(t) 的标准差；标准随机噪声 rand(t)～N(0,1)。

飞行仿真所采用机型为“DELTA”[23]，与纵向运动相关的定常平飞配平状态为：u0=75 m/s，w0=0 m/s，q0=0 rad/s，θ0=0.047 rad。飞机纵向小扰动状态方程（9）中，“DELTA”飞机的Mu值相对于其他气动参数为小量，在飞行仿真中将该值设为0。其他待辨识纵向气动参数的真实值为：Xu=-0.02，Xw=0.1，=0.14，Zu=-0.23，Zw=-0.634，=-2.9，Mw=-0.005，Mq=-0.61，=-0.44。在JSBSim 飞机气动力配置文件中设置上述飞行动力学气动参数，在JSBSim 初始化配置文件中设置上述定常平飞配平状态为仿真初始状态，在JSBSim 脚本设置文件中设置飞行状态参数的输出频率为64 Hz。分别以10 个幅值与周期不同的升降舵含噪声倍脉冲信号和10 个幅值与周期不同的升降舵含噪声3211 信号激励作为输入，通过JSBSim 求解器得到无噪声飞行仿真数据。含噪声飞行仿真数据通过在无噪声数据中添加噪声水平2%的随机噪声获得。图4 为升降舵含噪声3211激励输入下的纵向飞行参数随时间变化图。

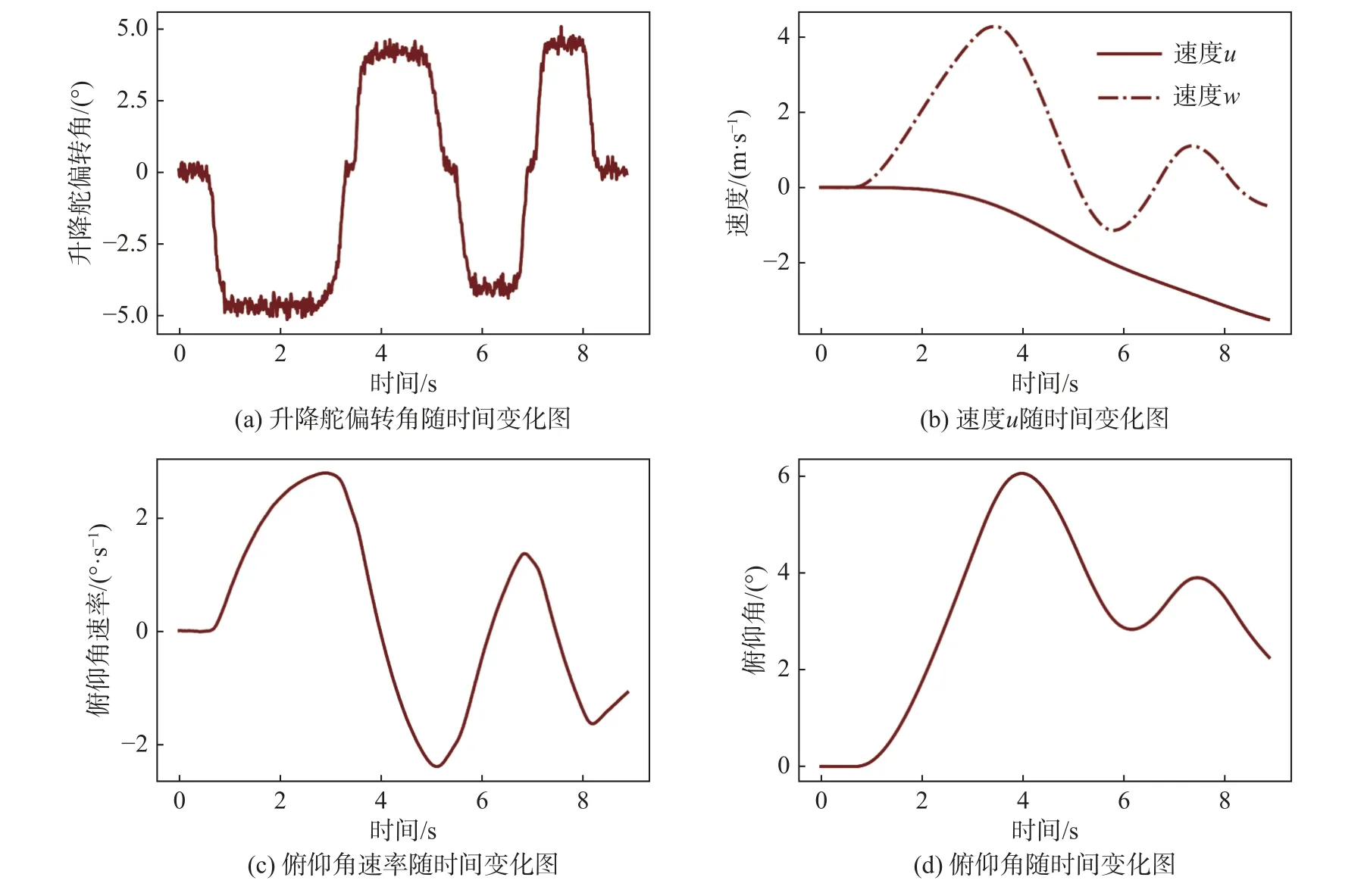
图4 升降舵3211 激励下纵向飞行参数随时间变化图Fig.4 Time history of longitudinal flight parameters under 3211 activation of the elevator

4 模型验证

气动参数辨识算法模型基于PyTorch 开源机器学习框架实现。随机从JSBSim 飞行仿真数据中选择5 000 组数据作为PINN 网络气动参数辨识方法研究的数据集，并将该数据集以80%和20%的比例随机划分为训练集与测试集。PINN 网络训练过程中主要超参数设置为：训练数据批量大小为512，学习率为0.001，所有训练集数据迭代训练次数为10 000。

基于无噪声飞行仿真数据的PINN 网络飞机纵向气动参数辨识结果及对应误差如表2 所示，基于含噪声飞行仿真数据的气动参数辨识结果及对应误差如表3 所示。无噪声时，9 个辨识参数中辨识误差最大的是Mw，其相对真值的误差为1.80%，这主要是因为Mw相对于其他待辨识气动参数小一个数量级，在PINN 网络误差反向传播、梯度下降及参数更新过程中相对更容易产生累积误差。含噪声时，待辨识参数中辨识结果误差最大的是Xδe，其相对真值的误差为4.64%。同时，含噪声时的待辨识参数的相对误差比无噪声时的结果整体上略微偏大。

表2 无噪声时PINN 气动参数辨识结果及对应误差Table 2 Results and errors of aerodynamic parameter identification by PINN without noise

表3 含噪声时PINN 气动参数辨识结果及对应误差Table 3 Results and errors of aerodynamic parameter identification by PINN with noise

为进一步验证基于PINN 网络的飞机气动参数辨识方法的效果，分别选取一组不在训练数据集中的完整升降舵激励信号，测试无噪声、含噪声PINN 网络的预测输出速度u、速度w、俯仰角速率q。图5、图6 分别为无噪声时一组升降舵倍脉冲激励、含噪声时一组升降舵3211 激励输入下，PINN 网络u、w、q的预测输出与真实值对比图。为了更清晰地展示对比情况，无噪声时选取t=0.5～1.0 s 时间范围，含噪声时选取t=2.0～2.5 s 时间范围。由图可见，无论纵向动力学飞行仿真数据中是否含有噪声，相对速度u、速度w、俯仰角速率q的预测误差总是偏大，这也与表2、表3 中气动参数辨识相对误差的分布表现一致。无噪声时，与u、w、q相关的气动参数辨识的最大相对误差分别为0.15%、0.14%、1.80%；含噪声时，与u、w、q相关的气动参数辨识的最大相对误差分别为4.64%、1.39%、2.60%；无论是否含有噪声，与w相关的气动参数的最大相对误差总是小于与u、q相关的气动参数的最大相对误差。

图5 无噪声时PINN 网络的预测输出与真实值对比图Fig.5 Comparison between the PINN prediction and the real value without noise

图6 含噪声时PINN 网络的预测输出与真实值对比图Fig.6 Comparison between the PINN prediction and the real value with noise

由于本文采用梯度下降法训练PINN 网络，其中与u、w、q相关的物理方程正则项约束在加入损失函数时权重均设为1，而与w相关的物理方程正则项以更大的梯度更新相关气动参数，所以导致与w相关的气动参数的相对误差较小。Wang 等[24]指出，在PINN 网络训练过程中，可以通过调整损失函数中不同组成成分之间的权重，使得其梯度值大小趋于一致，来改善PINN 网络的收敛情况。

一般来说，在飞机气动参数辨识工程应用领域，气动参数辨识结果的相对误差不大于10%就可采纳[25]。综上所述，基于PINN 网络的飞机气动参数辨识方法可行且有效，并对含噪声飞行数据的气动参数辨识具有一定的泛化能力。

5 结论

本文在传统神经网络气动参数辨识方法基础上，提出了一种基于PINN 网络的飞机气动参数辨识方法。该方法可以将含待辨识参数的飞机飞行动力学方程作为正则项加入到损失函数，通过PINN 网络梯度下降与参数更新，直接辨识得到气动参数。与极大似然法等工程辨识算法相比，该方法不需要给出待辨识参数的初始估计。与基于传统神经网络气动参数辨识方法相比，基于PINN 网络的辨识建模方法可以显著减少建模数据需求，也能提高建模精度。同时，针对纵向飞行状态空间模型辨识，通过JSBSim 飞行仿真验证，获得了在无噪声和含2%噪声仿真数据时9 个待辨识参数中辨识结果的最大相对误差（分别为1.80%、4.64%）。研究结果表明，基于PINN 网络的飞机气动参数辨识方法具有可行性，并对含噪声飞行数据的气动参数辨识具有一定的泛化能力。

后期，针对基于PINN 网络的非线性飞行动力学系统（特别是含有时间延迟、过程噪声等复杂场景）的气动参数辨识，需要结合真实飞行数据进行进一步验证。