使用灰度矩阵分析光子灯笼模式控制性能波动

赵欣瑞， 董一甲， 宁永强， 林星辰， 朱洪波

（1. 中国科学院 长春光学精密机械与物理研究所，长春 130031；2. 中国科学院大学，北京 100049）

1 引 言

随着半导体激光在机械加工、光纤通信等领域应用的发展，大功率、高稳定性与高基模成分比的高质量半导体激光的需求越来越大[1-5］。半导体激光的光纤合束损耗低，但受到多个因素的限制，如光纤热效应会造成模场收缩与横模振荡，输出端少模光纤会引入高阶模式等[6-7］。搭配主动模式控制系统的光子灯笼能够实现全光纤结构的相干光合束，是光合束的理想器件，但其输出光仍存在模式波动[8-9］。为了进一步提升大功率半导体激光合束光的稳定性，需要一种能在模式振荡下准确分析光子灯笼模式控制能力波动的评估技术。

目前，模式控制能力评估技术主要有间接测量与直接测量两类。间接测量主要包括基于空间光调制器滤波技术的计算机全息图法[10-13］与相干光滤波法[14-15］。这类技术能实现输出光模式的实时分解，但计算机全息图法需要预设输入光的模式成分，对于同类型器件的先验知识要求较高；相干光波法可以直接分解模式，不过当需要分解的光模式数目较多时，对空间光调制器尺寸、能力，以及实验对准精度的要求都会增加，这降低了它的适用性。直接测量主要包括光束质量因子与模式功率测量两种。2021 年，Zhou 等通过数值计算，使用3×1 光子灯笼实现了三路激光非相干合束时输出激光束的光束质量因子下限为M2=1.75，7 核光子灯笼的输出光的光束质量因子下限为M2=2.7，并以此来评估光子灯笼用于激光合束时的能力[16］。但这种光束质量因子测量方案下，合束功率超过光子灯笼的横模振荡阈值时，横模振荡造成的光束并不稳定会导致无法测量M2；即使在横模振荡阈值以下，光子灯笼的光纤包层中存在的干扰光也会影响M2的测量[17-18］；当出现意外的高阶模式时，M2的测量结果会低于1 从而失效[19］。直接测量的另一种方法是利用另一个模式选择光子灯笼结构将输出光分解后测量不同模式的功率，以此探究光子灯笼在模式复用与解复用上的应用潜力[20-21］。因为需要额外的结构，该方法同样不适用于半导体激光合束过程中光子灯笼的模式控制能力评估。

一种新的思路是通过评估锥形光纤区域的能力来分析光子灯笼性能。Savovi'c 等最早于2019 年提出基于实验测定光纤输出光的远场角功率分布方差变化率来计算光纤耦合系数，从而表征光纤模式控制能力的方案，并不断扩展到多种类型光纤的能力评估上[22-23］。然而，当输出光的稳定性较低时，基于实验进行光子灯笼的耦合系数的测定存在困难。为了克服上述技术的不足，本文采用灰度提取算法提取远场光场灰度矩阵，使用矩阵方差替代远场光场角功率分布方差来表征耦合系数，进而分析光子灯笼模式控制能力波动的情况，同时测量输出合束光质量与合束损耗曲线，分析了光子灯笼模式控制能力波动给合束效果带来的影响。

2 原 理

2.1 光子灯笼模式控制能力波动分析系统

图1 为自主研制的光电集成系统，用来分析光子灯笼模式控制能力波动。整个系统由3 部分组成：（1）976 nm 单频半导体激光器，具有3 路输出光纤，单路基模半导体激光的输出功率≤100 mW；（2）搭配主动模式控制系统的3×1 光子灯笼相干光合束系统；（3）光场分析系统。该系统的基本工作原理为：使用基于随机并行梯度下降算 法（Stochastic Parallel Gradient Descent Algorithm，SPGD）的主动模式控制系统控制光子灯笼实现相干光合束并抑制横模振荡效应，借助光束质量分析仪SP620 装配的CCD 相机获取多帧光子灯笼输出的合束光远场光场，输入程序后使用灰度提取算法计算灰度值矩阵分布方差的方差（Variance of Distribution Variance of Gray Value Matrix，VDVGM），以此评估光子灯笼在不同合束功率下的模式控制能力。

实验过程中，半导体激光器输出三路相同功率的基模半导体激光，在3×1 光子灯笼中发生合束，合束光经过非偏振平板分束镜被分为两路。其中，A 路功率占比为90%，经过凸透镜收束后进入CCD，CCD 拍摄的远场光场图像输入电脑端进行灰度提取与分析；B 路功率占比为10%，经过凸透镜聚焦后输入正中心装配25 μm 小孔的DET100A2 光电探测器，以测量透过小孔进入光电探测器的光功率，即轴上功率。功率信号被转换为电流信号后输入SPGD 系统，输出三路电压信号控制3×1 相位调制器阵列，这样做的目的是控制多路光发生相干合束，确保输出合束光的主要成分为基模，进而保证光子灯笼的性能分析符合理论推导条件。在输出端记录到基模轮廓的半导体激光合束光输出后，降低系统迭代系数的量级，这样可以适当降低对横模振荡效应的抑制效果[24］，降低光束稳定性，以便于模拟模式振荡存在时光子灯笼的性能。

2.2 基于方差系数的光子灯笼临近模耦合能力评估

在使用光子灯笼实现激光合束时，输出的合束光场振荡的主要诱因是光纤热效应造成的横模振荡，本质是临近模式之间的能量转移造成输出光模式成分不断地变化。因此，联立Gloge 功率流方程与耦合模理论来求解光纤耦合系数[25-27］，以此分析光子灯笼锥区光纤中的模式耦合过程，这是描述光子灯笼模式控制能力的可行方案。同时，考虑光纤波导的特性与半导体激光在光纤中发生的临近模耦合过程，将合束光场作为发射条件和光纤长度的函数构建方程，求解光场横向功率分布与光子灯笼对其中临近模耦合过程控制能力的关系。

在3×1 光子灯笼结构中，3 路合束光经由3根单模光纤输入到光子灯笼的锥区，在锥区耦合并激发多个横模，其中被输出端支持的模式进入输出端，不支持的高阶模被包层吸收产生模式损耗。这一传输过程可以表征为时间无关的光传输方程[28］，即：

其中：∂P(θ，z)为光波导的功率分布；α(θ)为模态衰减；d(θ)为光纤结构对应的耦合系数；Δθ为相邻模组间的角间距，当传播的光波导波长为λ时，对于纤芯直径为a，纤芯折射率为n1的光纤结构，Δθ=λ/4an1；z为光波导在光纤中的传输距离；θ为光波导输入路径与光纤中心轴的夹角。实验使用熔融拉锥法制备3×1 光子灯笼，其锥区的纤芯与包层折射率差为0.55%，在此结构下可以将离散模谱近似为模态连续体。根据临近模耦合理论，相邻模态间的功率耦合占到模态耦合的主要部分。光子灯笼锥区由对称排布的3 路单模光纤熔融拉锥制成，这使得入射光子灯笼锥区的3 路入射方向与光纤中心轴夹角θ相同，且保证多路输入光的角度均在引导模区域内。因此，输出端的少模光纤的模态衰减是可忽略的常量，即α(θ)=α0，α0为一个固定常量。同样忽略作为常量的传统损失，简化耦合系数[23，29］，同时根据Olshansky 的分析简化光纤中的耦合系数，最终得到：

假定D为常数，将P(θ，z)视为概率分布函数进行求解，最终将耦合系数表征为：

其中σ2z为光场的远场角功率分布方差。

对于稳定性较差的光束，其远场光场随传输长度的变化有两方面：一是输出光发散角造成的光场面积变大，二是模式振荡对于光场形状的影响。当使用灰度提取算法提取整个光场的功率分布情况时，发散角对光场面积的影响得以避免，模式振荡对于光场形状的影响成为主要分析对象。此时，可以使用固定位置处的CCD 拍摄的远场光场图的角功率分布方差变化率，代替远场角功率分布方差随传输距离变化的实验测量结果，进行光子灯笼能力波动的分析。

2.3 灰度提取算法原理及误差分析

图像特征值分析广泛应用于边缘提取、内容识别等领域[30-33］，灰度是图像的主要特征之一。本文基于图像识别数值化技术提出了一种灰度提取算法，核心思想是将光场的功率分布情况转化为灰度值矩阵，计算VDVGM 来表征光子灯笼在相干光合束过程中模式控制能力随合束功率的波动情况。光场的角功率分布方差是一个描述光场在空间频域上统计特性的物理量，主要用于反映光场在不同空间频率上功率分布的均匀程度。因此，可以通过提取图像各像素点亮度生成灰度矩阵，计算其方差来实现这一描述。该方法可以降低测量难度，同时提升光场的光强分布分析精度，增强光场角功率分布方差测量的实时性。

为了降低环境光对于光场角功率分布方差测量与计算的影响，在光束质量分析仪SP620 每次开始拍摄前都进行去背景光处理。首先在SP620 采集的固定19 帧图像中心727×727 像素尺寸内采样，确保背景光相同。如图2（a）所示，采样后每幅光场图的背景光保持为均匀一致的深色，在灰度矩阵中表现为24～30 内的较低矩阵值。当输出功率过高时，SP620 获取的远场光场会存在饱和白点，白点会掩盖功率差异，所以通过调节不同合束功率下SP620 的曝光参数来确保灰度值读取结果有效，并把曝光参数添加到最终的数据处理过程中来保证结果的准确性。

图2 光场图像的采集与处理Fig.2 Sampling and processing of light field image

各像素点灰度值是通过给三通道彩色图的R，G 与B 通道分别赋予不同权重后计算得到的，这样操作的目的是分离亮度与色度，实现亮度的独立计算。光场的各像素点振幅决定了亮度，各点亮度被提取为0～255 之间的整数灰度值，用于后续方差计算。由于光场功率分布的复杂性，以整数灰度值描述光场功率分布会引入误差，同时使用SP620 拍摄光场时也可能引入测量误差。为了分析这两部分误差，这里以合束功率为150 mW 时获得的一张采样后的远场光场图2（a）为例，根据从中提取的灰度矩阵复原生成彩色光场图，如图2（b）所示。

将两幅图像的RGB 三通道分离，分别提取灰度直方图进行匹配，计算三通道的平均相似度。如图3 所示，两幅图在RGB 三个通道内的灰度直方图曲线都表现出较高的重叠度，三通道相似度的平均值达到99.827%，这说明灰度提取算法对于远场光场功率分布的描述误差率＜0.2%，说明该误差对计算结果的影响较小，可以忽略。

图3 原光场图与根据灰度矩阵恢复得到的复原图的三通道灰度值对比Fig.3 Comparison of gray value of three channels between original light field image and restored image obtained according to gray matrix recovery

3 实验结果与分析

实验室制备的光子灯笼输入端使用商用康宁单模光纤（Single Mode Fiber， SMF），芯径为8.3 μm，包 层 直 径 为125 μm，纤 芯 折 射 率 为1.468 1，芯包层折射率差为0.36%。输出端为OFS 两模渐变折射率光纤，传输976 nm 激光时支持多种模式，其中Lp01与Lp11两种模式的衰减＜0.21，为光纤主要支持的模式，也是光子灯笼锥区的主要模式。为了对比，本文给出了两个不同合束功率下的输出光场与标准基模和一阶模的输出光场，如图4 所示。图4（a）与4（b）为实际测量光场，由于存在环境光的影响，光场背景也存在一定亮度；图4（c）～4（e）为仿真得到的标准模式，不存在环境光故而背景颜色较深。

图4 不同合束功率下的输出光场与标准基模Fig.4 Output light field and standard modes with different combiming powers

在0～300 mW 内改变合束功率，测量输出光的最大高斯拟合度来分析输出合束光的主要模式成分，结果如图5 所示。其中，高斯拟合度来自SP620，它在捕获光场的2D 图像后，SP620 输出横纵两个方向的功率分布曲线，分别与高斯曲线拟合后求均值即可得到高斯拟合度。在高斯拟合度计算过程中，图4（a）～4（e）的背景光在轮廓曲线中均表现为平直的山脚，对光束轮廓曲线的形状没有影响，故不会为光束模式成分分析引入误差。当合束功率＜270 mW 时，合束光的高斯拟合度均在0.55～1 之间，这证明主动模式控制保证了输出合束光的主要成分为基模。

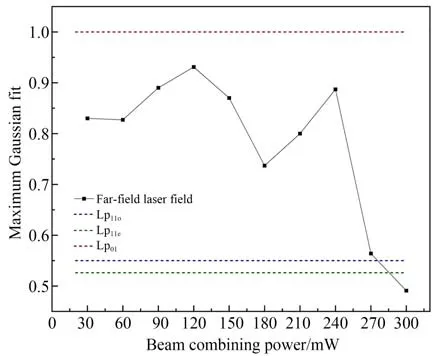
图5 输出光远场光场的最大高斯拟合度曲线Fig.5 Curve of maximum Gaussian fitting degree of farfield light field of output light

实验按照30 mW 的步长改变合束功率并测量VDVGM，光子灯笼模式控制能力与合束损耗随合束功率波动的曲线如图6 所示。随着合束功率的升高，模式间的耦合会加剧，给合束损耗带来正面影响，所以实际的合束损耗是模式耦合效应与光子灯笼模式控制共同作用的结果。当合束功率在60 mW 附近时，VDVGM 较低，光子灯笼的模式控制能力较弱，导致实际合束损耗曲线的斜率较大，对应输出光的高斯拟合度在0.8 附近。当合束功率在120 mW 附近时，VDVGM 较高，意味着光子灯笼的模式控制能力较强，合束损耗曲线斜率相较之前变小。因为光子灯笼较高的模式调控能力抑制了能量向高阶模的转移，减少了被光纤包层吸收的高阶模功率，从而降低了合束损耗，所以合束功率从90 mW 增加到150 mW 时的合束损耗增幅远小于合束功率从30 mW 增加到90 mW 时的合束损耗增幅。同时在120 mW 合束功率下测到了一个高的高斯拟合度与具有基模轮廓的输出光，如图4（a）所示。当合束功率在180 mW 附近时，VDVGM 降低，导致合束损耗曲线出现一个明显的上升。当合束功率在210 mW 附近时，VDVGM 升高，光子灯笼中的模式耦合被很好地控制，合束损耗降低，也因此得到了图4（b）所示的具有基模轮廓的合束光输出，但是由于合束功率为210 mW 时的VDVGM 低 于120 mW，所 以 图4（b）的 光 场 相较于图4（a）具有一些额外的旁瓣，高斯拟合度也更低。在240 mW 附近输出光的高斯拟合度存在一个极大值，这是由于合束功率从210 mW 升 高 至240 mW 时，功 率 升 高 造 成 的 模 式耦合引起的能量向高阶模转移增加，相较于功率较低时更强烈，导致大量高阶模功率被光子灯笼输出端少模光纤的包层吸收，剩余的基模光进入纤芯输出，因而具有较高的高斯拟合度，同时具有一个较大的合束损耗曲线斜率。当合束功率进一步提升时，VDVGM 下降但基本保持在一个较为稳定的水平，同时功率升高引起的光纤热效应导致的模式振荡随功率升高变强，造成输出光质量急剧下降，合束损耗急剧上升。

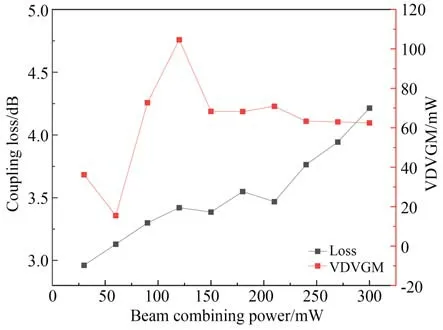
图6 VDVGM 与合束损耗随合束功率的变化Fig.6 Variation of VDVGM and beam combining loss with beam combining power

实验结果表明，随着合束功率的升高，光子灯笼模式控制能力存在一个非线性波动，这导致合束损耗曲线的非线性增加与最大高斯拟合度曲线的波动。根据VDVGM 的测量结果，光子灯笼模式控制能力存在达到峰值的合束功率点，合束损耗曲线在该合束功率附近斜率降低，光子灯笼的模式控制能力提升，验证了该方法表征光子灯笼模式控制能力的可靠性。

4 结 论

本文针对现有光子灯笼性能评估方法设备复杂、实验要求高、适用范围小的缺点，提出一种简单、即时的技术方案来测量光子灯笼模式控制能力随合束功率变化的波动情况。理论推导证明，该方案能够实现输出光稳定性较低时对光子灯笼模式控制能力波动的实时测量与分析。光场图和复原图的灰度直方图曲线相似度结果大于99%，证明了该方案对光场描述的可靠性。使用该方法进行了弱主动模式控制下3×1 光子灯笼在输出不稳定光场时的模式控制性能波动分析，高斯拟合度与光损耗测量结果验证了使用VDVGM 表征光子灯笼性能的准确性。实验结果表明，光子灯笼模式控制能力波动会影响其输出光的质量与光合束损耗变化率，模式调控能力的升高能够在一定程度上提升光束质量同时降低光合束损耗的增幅。本文提供了一种简单、即时且输出光稳定性要求低的光子灯笼模式控制性能波动测量方法，适用于模式振荡存在时光子灯笼模式控制能力随合束功率变化的波动分析，为进一步提升光子灯笼横模振荡阈值提供了可靠的评价方案，有助于大功率半导体激光稳定性的进一步提升。