基于离散绕组的磁场式时栅位移传感器及误差特性

陈自然， 张桁潇， 何智颖， 陈鸿友， 余海游

（1. 重庆理工大学 机械检测技术与装备教育部工程研究中心，重庆 400054；2. 中煤科工集团重庆研究院有限公司，重庆 400039；3. 时栅传感及先进检测技术重庆市重点实验室，重庆 400054）

1 引 言

精密位移测量技术及器件是高档数控机床、高端仪器设备等精密高端装备的核心技术和关键功能部件，是实现精密定位与控制的“眼睛”[1-4］，直接决定着系统的性能。光栅采用又精又密的栅线作为测量基准，其加工精度决定测量精度，其密度决定测量分辨力[5-7］。目前，市场上高精度增量式直线光栅的栅距为20 μm，测量精度为±3 μm。为提高测量精度和分辨力，世界领先的德国HEIDENHAIN 公司生产的LIP201 直线光栅[8］的栅距提高到2.048 μm，测量精度达到±1 μm。上海光学精密机械研究所为实现纳米级的测量精度，使用超精密激光设备 研 制 了 栅 距 为830 nm 的 光 栅[9］，测 量 精 度 提高到50 nm。光栅的测量精度越高，对栅线刻划的均匀性和一致性要求越高，制造难度呈几何指数增长，此类精密光刻技术已逼近极限，很难再进一步提高。同时，光栅使用过程中易受到光电池安装位置、指示光栅与标尺光栅夹角误差和衍射光强等因素的影响[10-11］，导致信号质量不稳定，严重影响光栅的测量精度。因此，光刻精度和安装误差是影响光栅测量精度的两个重要因素。

针对上述问题，前期课题组提出利用时间提高位移测量精度的方法，发明了时栅位移传感器[12-17］。本文在此基础上提出了基于离散绕组的磁场式时栅位移传感器，通过设计毫米级尺寸的激励绕组和感应绕组的形状与排布输出位移感应信号，实现微米级测量精度，降低了传感器的制造难度。

2 工作原理

基于离散绕组的磁场式时栅位移传感器结构主要包含动尺和定尺，动尺和定尺在空间上正对平行安装，并保持一定的间隔距离δ，如图1所示。其中，动尺包含基体和正弦形感应绕组阵列，定尺包含基体和激励绕组阵列。定尺上均匀布置两行边长为d的离散矩形激励绕组，按间隔d等间距排布，其中第一行构成正弦激励绕组，第二行构成余弦激励绕组。同行相邻激励绕组依次施加相位相差180°的激励电流信号，如下：

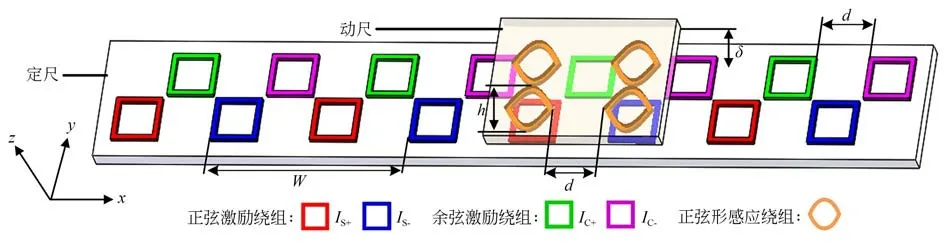
图1 磁场式时栅位移传感器总体结构Fig.1 Overall structure of magnetic-field type time-gating displacement sensor

其中：Im为激励交变电流的最大幅值，ω为激励交变电流频率。

动尺包含4 组正弦形感应绕组，记为A，B，C，D，其中正弦形感应绕组A 和正弦形感应绕组B 按相同绕向串联，正弦形感应绕组C 和正弦形感应绕组D 按相同绕向串联，如图2所示。

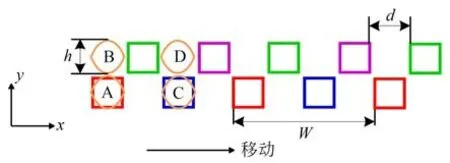
图2 感应绕组和激励绕组的位置示意图Fig.2 Position of induction winding and excitation winding

给定尺上的激励绕组通入正/余弦激励电流，当动尺与定尺产生相对位移时，根据电磁感应原理可得正弦形感应绕组A，B 在一个激励绕组周期极距W内的感应电动势，即：

其中：k为比例系数，h为正弦形感应绕组的高度，W为极距，x为动尺的运动位移。

同理，正弦形感应绕组C，D 在一个激励绕组周期极距W内的感应电动势为：

由叠加定理可得正弦形感应绕组A、B 串联后的感应电动势以及正弦形感应绕组C、D 串联后的感应电动势，如下：

其中：K=

正弦形感应绕组A 和正弦形感应绕组C 构成差动传感结构，正弦形感应绕组B 和正弦形感应绕组D 构成差动传感结构，可有效消除共模信号干扰。因此，正弦形感应绕组A，C 与正弦形感应绕组B，D 串联后的叠加信号为：

式（5）即为传感器输出的携带位移信息的行波信号，行波信号的相位变化反映动尺的运动状态，并随运动位移发生周期变化，与同频参考信号比相获得时间量Δt，进而获得测量位移量Δx，位移解算方案如图3 所示。在动尺运动过程中，感应绕组产生输出的感应信号Ux，经过滤波电路、放大电路的预处理后，由整形电路整形成方波信号，之后输入FPGA 模块与同频参考信号Uf进行比相，由高频时钟脉冲插补计数求出相位差的时间量Δt，由此求得运动方向的位移量为：

图3 位移解算方案示意图Fig.3 Schematic diagram of displacement solution scheme

其中：N为动尺在运动方向上运动的完整对极数，T为参考信号的时钟周期。

传感器的测量分辨力可以表示为：

其中：L为量程，N为对极数，fe为激励信号频率，fr为用于插补相位差的高频时钟频率。

3 传感器误差分析

3.1 驻波信号幅值不等的误差分析

根据式（5）可知，被测位移主要体现为行波信号的相位变化，因此行波信号质量会直接影响传感器的测量精度。但加工误差与人为因素在测量过程中会导致测量误差，根据基于离散绕组的磁场式时栅位移传感器的结构和工作原理，这里对两路驻波信号的幅值不等、相位非正交造成行波信号发生的变化展开讨论。

磁场式时栅位移传感器在测量过程中，由于激励信号误差和安装误差的影响，合成行波信号的两路驻波信号幅值不等，使行波信号的相位与理论相位之间存在偏差。以正弦形感应绕组A，B 为例，当感应绕组输出的信号幅值不等时，式（2）改写为：

其中：KA，KB分别为正弦形感应绕组A，B 输出驻波信号的幅值。

三角函数辅助角公式如下：

根据式（9）对两路驻波信号进行叠加，得到的行波信号如下：

根据式（9）对式（4）进行变形，得到：

将式（10）与式（11）的相位作差可得到由两路驻波信号幅值不等造成的误差，即：

反三角函数的表达式如下：

根据式（13）对误差表达式进行简化，得到：

由上述分析可知，当合成行波信号的两路驻波信号的幅值不等时，测量结果会引入2 次谐波误差。

3.2 驻波信号相位非正交分析

两路驻波信号在空间上的相位非正交，使得行波信号中引入误差，主要因为传感器产生了安装误差。此刻设正弦形感应绕组A，B 输出的驻波信号的幅值相等、初相位不相等，则表达式为：

其中φ为两路驻波信号空间上的相位差值。

根据叠加定理，两路驻波信号叠加产生的行波信号为：

根据式（11）和式（12）可得由两路驻波信号空间相位非正交造成的误差公式，即：

由式（17）可知，当两路空间相位非正交的驻波信号合成行波信号时，误差主要含有0 次谐波（直流分量）和2 次谐波。

4 仿真与误差分析

为研究激励信号误差和动尺的安装误差对传感器输出的行波信号的影响，使用Maxwell 电磁仿真软件进行有限元仿真。激励信号误差为激励信号幅值不相同，动尺的安装误差一般分为3 种情况：动尺相对于定尺沿X轴、Y轴和Z轴发生了旋转（分别称为俯仰、翻转和偏摆），如图4 所示。传感器的基本仿真参数设置如下：运动方向极距W为24 mm，激励绕组的高度和宽度均为5.8 mm，直径为0.2 mm，感应绕组高度和宽度均为6 mm，直径为0.3 mm，感应绕组阻抗为1 MΩ，感应绕组和激励绕组的气隙高度为0.6 mm。

图4 传感器动尺的不同安装姿态Fig.4 Different installation attitudes of sensor moving ruler

4.1 激励信号幅值不相同仿真

仿真中传感器的动尺移动24 mm，感应信号刚好变化一个完整的周期。在正弦激励绕组和余弦激励绕组中通入设定好幅值的激励信号，得到在两路激励信号幅值不同的情况下仿真输出的行波信号，如图5 所示。

图5 对极内不同激励信号幅值下的仿真结果Fig.5 Simulation results under different excitation signal amplitudes within a pitch

计算图5（a）～5（d）每条正弦曲线的初相位角，并与理论的初相位角相减，得到各空间位置的初相位误差，最后转换为对应的误差曲线，如图6（a）所示，采用傅里叶变换分析误差曲线，结果如图6（b）所示。

由图6 可知：当两路激励信号的幅值为1 A和1 A，位移误差的峰峰值为18.96 μm；当幅值为1 A 和2 A，位移误差的峰峰值为25.21 μm；当幅值为1 A 和3 A，位移误差的峰峰值为39.77 μm；当幅值为1 A 和4 A，位移误差的峰峰值为48.58 μm。不同激励信号幅值对应的位移误差主要包含直流分量和2 次谐波，当两路激励信号的幅值差距逐渐变大，直流分量和2 次谐波的幅值明显增大。

4.2 沿X 轴俯仰姿态的仿真

动尺相对于定尺绕X轴有一个俯仰角度α，如图7 所示。在仿真模型中，俯仰角度α分别设置为0°，1°，2°和3°，得到不同俯仰角度下仿真输出的行波信号，如图8 所示。

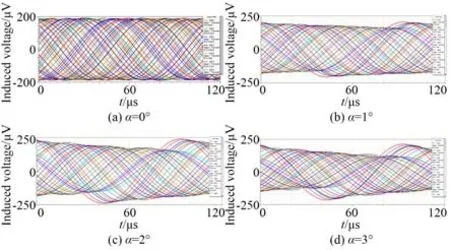
图8 对极内不同俯仰角度下的仿真结果Fig.8 Simulation results under different tilt angles within a pitch

计算图8（a）～8（d）中行波信号的初相位和理论初相位的误差，得到不同俯仰角度的误差曲线，如图9（a）所示，采用傅里叶变换分析误差曲线，结果如图9（b）所示。

由图9 可知：α为0°时，位移误差的峰峰值为18.96 μm；当α为1°时，位 移 误 差 的 峰 峰 值 为22.11 μm；当α为2°时，位 移 误 差 的 峰 峰 值 为41.08 μm；当α为3°时，位 移 误 差 的 峰 峰 值 为41.91 μm。不同俯仰角度下对应的位移误差主要包含直流分量和4 次谐波，在α从0°增大到1°的过程中，直流分量和4 次谐波的幅值减小，而在α从1°增大到3°的过程中，直流分量和4 次谐波的幅值逐渐增大。

4.3 沿Y 轴翻转姿态的仿真

动尺相对于定尺绕Y轴有一个翻转角度β，如图10 所示。在仿真模型中，偏转角度β分别设置为0°，1°，2°和3°，得到不同翻转角度下仿真输出的行波信号，如图11 所示。

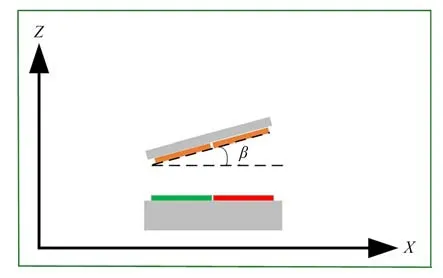
图10 动尺的翻转示意图Fig.10 Flipping diagram of moving ruler

图11 对极内不同翻转角度下的仿真结果Fig.11 Simulation results under different flip angles within a pitch

计算图11（a）～11（d）中行波信号的初相角和理论初相角的误差，得到不同翻转角度下的误差曲线，如图12（a）所示，采用傅里叶变换分析误差曲线，结果如图12（b）所示。

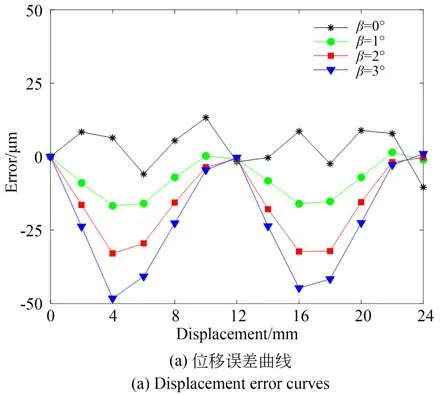
图12 对极内不同翻转角度的位移误差曲线和误差频谱Fig.12 Displacement error curves and error spectra for different flip angles within a pitch

由图12 可知：当β为0°时，位移误差的峰峰值为18.96 μm；当β为1°时，位移误差的峰峰值为20.58 μm；当β为2°时，位移误差的峰峰值为32.95 μm；当β为3°时，位 移 误 差 的 峰 峰 值 为49.26 μm。不同翻转角度下对应的位移误差主要包含直流分量和2 次谐波，并随翻转角度的增大，直流分量和2 次谐波的幅值也逐渐增大。

4.4 沿Z 轴偏摆姿态的仿真

动尺相对于定尺绕Z轴有一个偏摆角度θ，如图13 所示。在仿真模型中，设置偏摆角度θ分别为0°，1°，2°和3°，得到不同偏摆角度下仿真输出的行波信号，如图14 所示。

图13 动尺的偏摆示意图Fig.13 Deflection of moving ruler

图14 对极内不同偏摆角度下的仿真结果Fig.14 Simulation results under different deflection angles within a pitch

计算图14（a）～14（d）中行波信号的初相角和理论初相角的误差，得到不同偏摆角度下的误差曲线，如图15（a）所示，采用傅里叶变换分析误差曲线，结果如图15（b）所示。

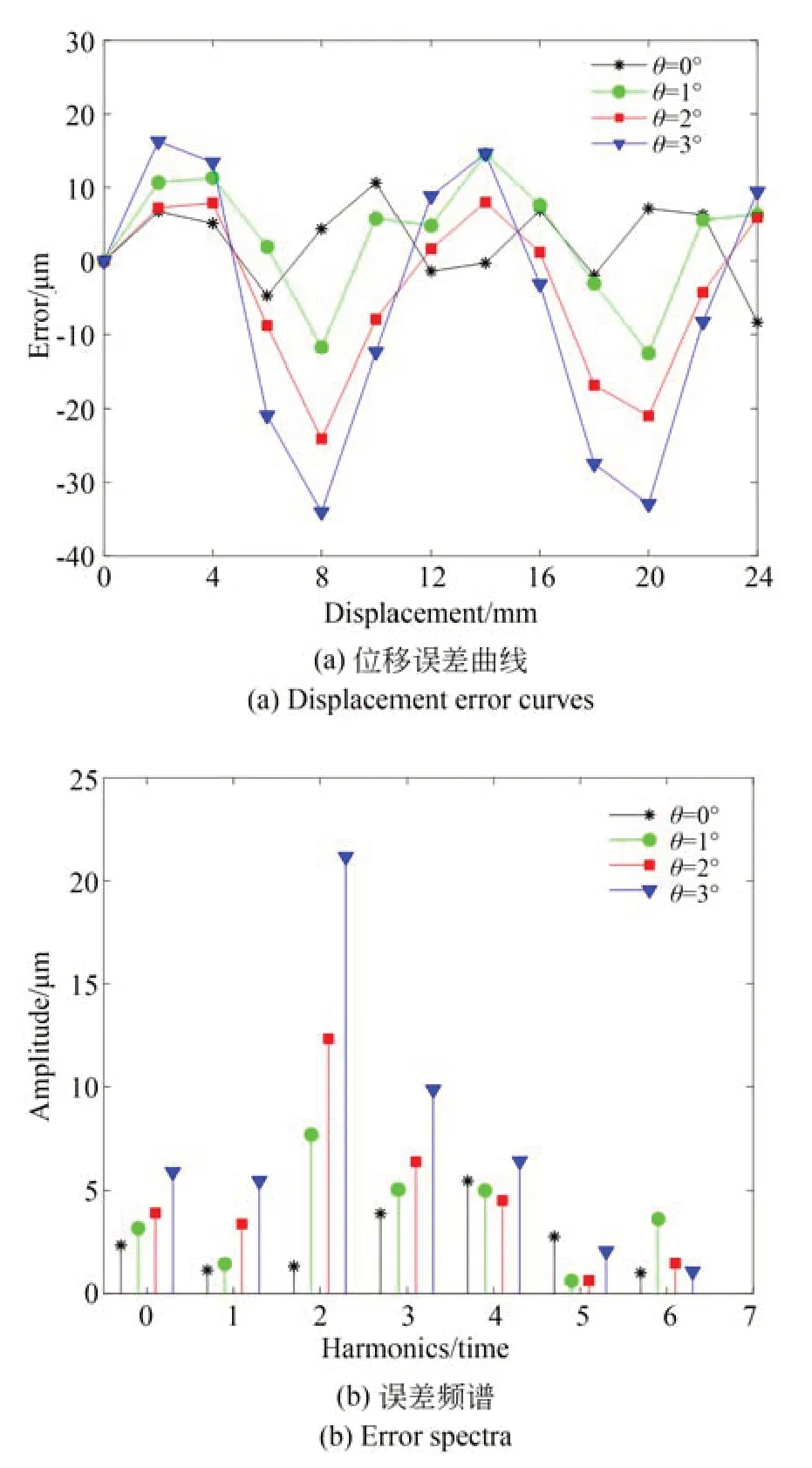
图15 对极内不同偏摆角度的位移误差曲线和误差频谱Fig.15 Displacement error curves and error spectra for different deflection angles within a pitch

由图15 可知：当θ为0°时，位移误差的峰峰值为18.96 μm；当θ为1°时，位移误差的峰峰值为27.11 μm；当θ为2°时，位移误差的峰峰值为32.07 μm；当θ为3°，位 移 误 差 的 峰 峰 值 为50.3 μm。不同偏摆角度下对应的位移误差主要包含2 次谐波，且随着偏摆角度的增大，2 次谐波的幅值也逐渐增大。

综上所述，仿真结果与理论推导基本相同，两路激励信号的幅值不相同、动尺沿X轴俯仰姿态、沿Y轴翻转姿态和沿Z轴偏摆姿态在测量精度中主要引入直流分量误差和2 次谐波误差。经分析，动尺沿Z轴偏摆姿态误差对测量精度的影响最大，沿Y轴翻转姿态误差影响次之，沿X轴俯仰姿态对测量精度的影响最小。

5 实 验

采用工艺成熟、价格相对低的印制电路板技术制作传感器样机，如图16 所示。激励绕组在空间上间隔1/4 极距等间隔、均匀排布。激励绕组分别通入频率为10 kHz的正/余弦激励信号，通入同相的激励信号的激励绕组按相反绕向串联。

采用美国AEROTECH 公司制造的直线电机模组PRO190LM-0500-T1-E3-MS1F-PL2-TAS，配置高性能驱动器BLMC-192-A，搭建如图17 所示的实验平台，整个系统的重复精度为±0.5 μm，系统的整体定位精度为±1 μm，分辨率为10 nm。

图17 时栅位移传感器误差特性实验平台Fig.17 Experimental platform for error characteristics of time-gate displacement sensor

实验中，动尺与定尺分别固定在导磁基体上，气隙高度为0.6 mm，由直线电机带动传感器的动尺沿导轨做直线运动。在运动过程中，传感器动尺的感应绕组通过与定尺产生的空间磁场耦合，感应得到直线电机运动平台的位移信号。感应信号在放大、滤波并整形成方波信号后，与FPGA 内部的参考信号进行比相，通过高频时钟脉冲进行计数得到位移测量值。实验采用Renishaw 激光干涉仪XL-80 作为测量基准标定传感器的测量精度，得到传感器的位移测量误差，整个实验平台结构如图18所示。

图18 时栅位移传感器样机Fig.18 Prototype of time-gate displacement sensor

图18 为传感器样机，直线电机带动动尺匀速运动24 mm，即1 个对极，每运动1 mm 信号处理电路的FPGA 芯片同步采集激光干涉仪数据和传感器运动位移数据。传感器安装较为理想，通过设置两路激励信号的幅值不同，进行对极内精度实验，获得如图19（a）和19（b）所示的对极内不同激励信号幅值的测量误差曲线和误差频谱。

然后，在两路激励信号的幅值为1 A 和1 A的条件下，对动尺在不同轴上发生安装偏差产生的测量误差进行实验。动尺沿X轴的俯仰角度α分别为0°，1°，2°和3°时得到的测量误差曲线如图20（a）所示，采用傅里叶变换进行分析，得到如图20（b）所示的误差频谱。

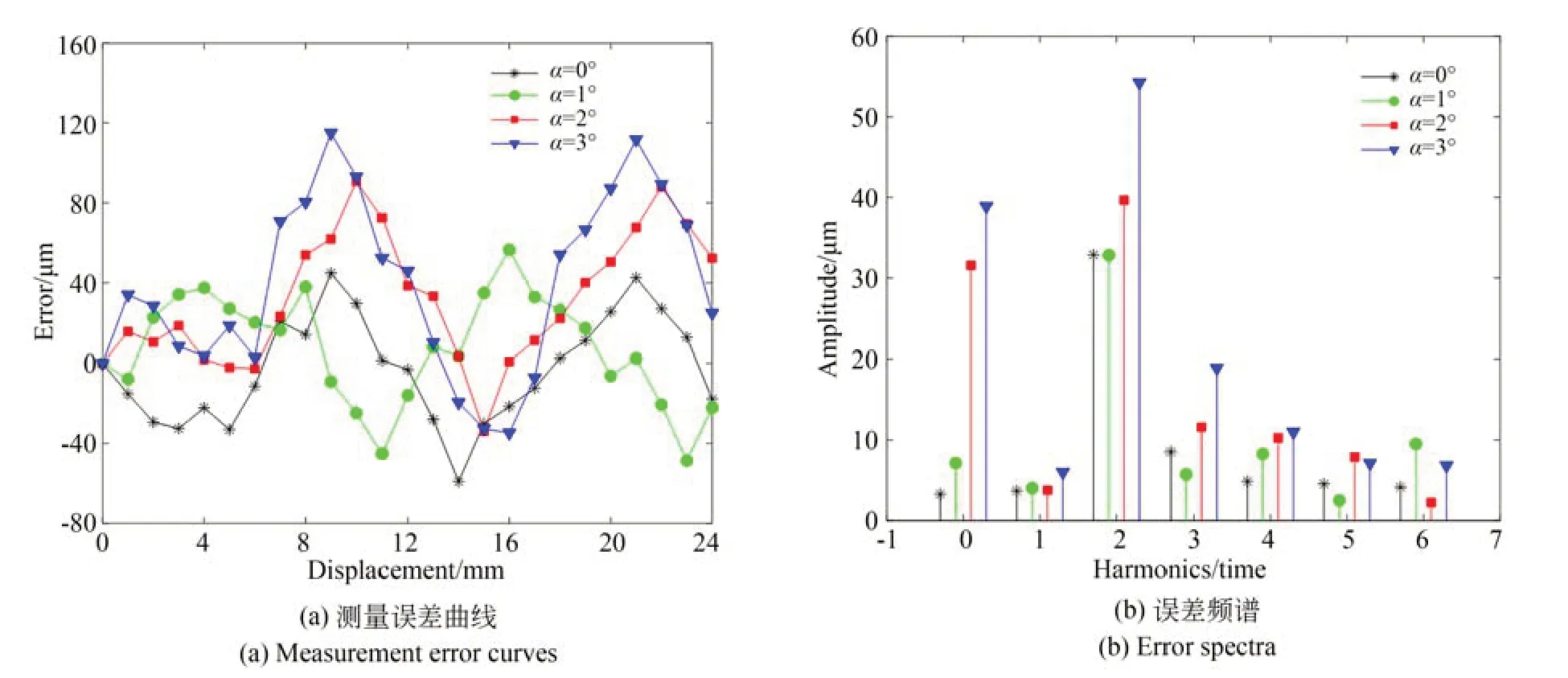
图20 对极内不同俯仰角度的测量误差曲线和误差频谱Fig.20 Measurement error curves and errors spectra for different tilt angles within a pitch

重新安装动尺，沿Y轴的翻转角度β分别为0°，1°，2°和3°时所得到的测量误差曲线如图21（a）所示，采用傅里叶变换进行分析，得到如图21（b）所示的误差频谱。

图21 对极内不同翻转角度的测量误差曲线和误差频谱Fig.21 Measurement error curves and error spectra for different flip angles within a pitch

再次安装动尺，沿Z轴的偏摆角度θ为0°，1°，2°和3°时得到的测量误差曲线如图22（a）所示，进行傅里叶变换得到如图22（b）所示的误差频谱。

图22 对极内不同偏摆角度的测量误差曲线和误差频谱Fig.22 Measurement error curves and error spectra for different deflection angles within a pitch

整理实验数据可知：（1）对极内不同激励信号幅值为1 A 和1 A，1 A 和2 A，1 A 和3 A，1 A和4 A 时，测量误差的峰峰值分别为103.95，168.23，231.31 和274.22 μm。当激励信号相同时，测量误差中包含的主要误差成分为2 次谐波；当激励信号不同时，测量误差中包含的主要误差成分为直流分量和2 次谐波，且随两路激励信号的幅值之差越大，直流分量和2 次谐波的幅值也越大。

（2）动尺的俯仰角度α为0°，1°，2°和3°时，测量误差的峰峰值分别为103.95，104.63，124.72，149.67 μm。当俯仰角度α为0°时，测量误差的主要成分为2 次谐波；当俯仰角度从1°开始增大时，测量误差的主要成分为直流分量和2 次谐波，且随俯仰角度的增大，直流分量和2 次谐波的幅值也增大。

（3）动尺的翻转角度β为0°，1°，2°和3°时，测量误差的峰峰值分别为103.95，114.32，135.12，166.29 μm。不同翻转角度下测量误差的主要成分相同，为2 次谐波，且随偏转角度的增大，2 次谐波的幅值也增大。

（4）动尺的偏摆角度θ为0°，1°，2°和3°时，测量误差的峰峰值分别为103.95，187.07，259.82，342.97 μm。不同偏摆角度下测量误差的主要成分相同，为2 次谐波，且随偏摆角度的增大，2 次谐波的幅值也增大。

在整量程144 mm 内，传感器安装较为理想、激励信号幅值为1 A 和1 A，得到的原始测量误差曲线如图23 所示，测量误差为-59.1～44.85 μm，测量误差的峰峰值为103.95 μm。采用谐波修正法[18］对原始测量误差进行修正，修正后测量误差为-2.85～1.65 μm，测量误差的峰峰值为4.5 μm。表1 为激励信号误差和安装误差对整量程内测量精度的影响。

表1 激励信号误差和安装误差对整量程内测量精度的影响Tab.1 Influence of excitation signal error and mounting error on measurement accuracy over entire scale （μm）

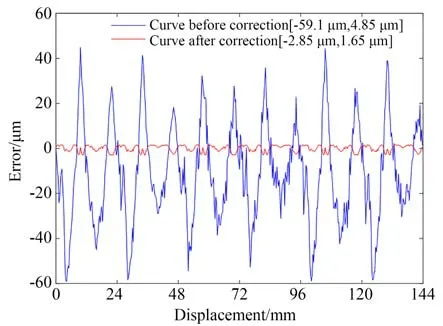
图23 整量程内谐波修正前后的测量误差曲线Fig.23 Measurement error curves before and after harmonic correction within full-range

由于传感器的量程L为144 mm，激励绕组和感应绕组的对极数为6，激励信号频率为10 kHz，FPGA 中进行插补的高频时钟脉冲频率为1.6 GHz，由式（7）计算得到该传感器的测量分辨力理论上可以达到0.15 μm。

6 结 论

针对高精度位移传感器难以加工的难题，本文利用组合测量原理，通过设计毫米级激励绕组和感应绕组的排布方式与形状实现微米级测量精度，研制了一种基于离散绕组的磁场式时栅位移传感器。对磁场式时栅位移传感器在激励信号幅值不等和动尺沿X轴俯仰姿态、Y轴翻转姿态和Z轴偏摆姿态下的误差特性进行了仿真和实验验证。仿真与实验结果表明：在对极内，两路激励信号幅值不等和动尺沿X轴俯仰姿态对测量误差中的直流分量和2 次谐波分量的影响较大，对其他频次谐波的影响较小；而动尺沿Y轴翻转姿态和沿Z轴偏摆姿态对测量误差中的2 次谐波分量的影响较大，对其他频次谐波的影响较小。因此，激励信号误差和安装误差在测量精度中引入直流分量误差和2 次谐波误差，其中2 次谐波误差为主要误差成分，仿真结果与实验结果基本相同。

在对极内和整量程中，两路激励信号幅值不等和不同的安装误差对测量精度均有较大影响。安装误差中，动尺沿Z轴偏摆姿态对测量精度的影响最大，动尺沿Y轴翻转姿态对测量精度的影响次之，动尺沿X 轴俯仰姿态对测量精度的影响最小。因此，在基于离散绕组的磁场式时栅位移传感器的安装过程中，应着重避免动尺沿Y轴发生翻转和动尺沿Z轴发生偏摆，确保两路激励信号的幅值相同，以保证传感器的测量精度。

最后进行整量程精度实验，在144 mm 量程内，传感器原始误差的峰峰值为103.95 μm，经谐波修正后测量误差的峰峰值为4.5 μm，传感器的分辨力为0.15 μm。综上表明，通过毫米级尺寸的激励和感应绕组实现微米级测量精度，可显著降低传感器的制造难度，具有重要的工程应用价值。