多电压等级直流系统大信号稳定性分析

2023-11-01吴彦伟欧嘉俊吴浚铭

电力系统及其自动化学报 2023年10期

吴彦伟，欧嘉俊，苏涛，王波，吴浚铭，穆涵

（1.广东电网有限责任公司广州供电局，广州 510620；2.南京南瑞继保电气有限公司，南京 211102；3.东南大学先进电能变换技术与装备研究所，南京 210096）

近年来，随着光伏、风电和储能装置的高度渗透，以及直流负荷的日益增长，电网的直流特征愈发明显[1-3]。由于直流系统可实现分布式新能源的并网及消纳，且不存在交流系统的无功、相位和频率问题，已逐渐成为国内外研究热点[4-6]。随着电力电子技术的快速发展，直流系统的控制更加灵活[7]，但众多电力电子设备间的复杂交互作用导致直流系统大扰动下的稳定性问题突出[8]。另外，恒功率负载CPL（constant power load）的负阻抗特性也是导致系统大信号失稳的主要原因之一[9-10]。

当系统受到大信号扰动时，并不满足线性化的假设条件，这意味着基于经典控制理论的小信号分析方法将不适用于评估系统在大扰动下的稳定性[11-12]。目前，李雅普诺夫第二法被广泛应用于分析系统的大信号稳定性[13-14]。但基于李雅普诺夫函数的大信号稳定性分析方法并不能给出系统稳定域的代数表达式，因此难以直接指导系统设计。而Brayton-Moser 混合势函数理论则可以直接用于分析非线性电路的大扰动稳定性，并得到系统稳定域的解析解[15-16]。

文献[17]建立了LC 滤波器和CPL 级联形式的直流系统的混合势函数，分析不同控制参数对系统大信号稳定性的影响。文献[18]分析了带CPL的双向buck变换器的混合势函数，得出在大扰动下控制器限幅对系统大信号稳定性的影响。由于实际负载变换器的响应速度要明显慢于理想的CPL，从而导致大信号稳定性分析得出的稳定性边界过于保守，为此文献[19]改进了CPL的简化模型。

混合势函数理论多被应用于单电压等级直流系统，而其在多电压等级直流系统中的应用研究较为匮乏。近年来，多电压等级直流系统由于可实现更大电压比，且便于接入不同电压等级负载而逐渐兴起[20-21]。文献[22]首次将混合势函数理论应用于简单三级级联系统，评估了其大信号稳定性，但并未考虑不同控制模式对系统大信号稳定的影响。

本文以简单三级级联Buck 变换器为例研究多电压等级直流系统的大信号稳定判据。首先，结合系统开环状态空间模型和混合势函数定理，讨论了源变换器在采用单电压环控制和双闭环控制下的模型简化方法，并提出通用系统大信号简化模型。然后，通过构造混合势函数方程，确定系统的大信号稳定域，并研究系统关键参数对大信号稳定性的影响。最后，通过案例分析和仿真实验，验证了理论分析的正确性。

1 多电压等级直流系统的状态平均模型

由Buck 变换器构成的具有两个电压等级的三级级联直流系统如图1所示。中压直流MVDC（medium voltage DC）母线和低压直流LVDC（low voltage DC）母线电压分别为vMbus和vLbus。其中，前两级变换器的状态空间平均方程为

图1 基于Buck 变换器的三级级联系统Fig.1 Three-stage cascaded system based on Buck converters

式中：vin为系统输入电压；RLx、iLx和uLx分别为电感Lx的串联等效电阻、电流和端电压，序号x=1，2；dx为占空比；Cx为输出滤波电容；iox为输出电流；iCPL为后级变换器的输入电流。

对于CPL，当母线电压骤降或突然升高时，其输入电流将沿着反方向变化，从而进一步加剧电压波动。因此系统中后级变换器在大信号分析中可以等效为一个受控电流源，其电流值iCPL=PCPL/vLbus，其中，PCPL为后级变换器吸收的有功功率。因此根据式（1）可得三级级联系统的状态平均模型如图2所示。

图2 系统的状态平均模型Fig.2 State-average model of system

2 混合势函数理论

混合势函数理论由Brayton 和Moser 在1964年提出[1]，它为非线性电路的暂态稳定性分析提供了统一的研究方法，也为非线性电路大扰动下的稳定性提供了判据[2]。该方法首先基于非线性电路的特性与结构，构建待研究系统的混合势函数；然后，根据混合势函数的特点对其进行重构，以满足相应的稳定性判别定理所要求的形式；最后，应用相应定理得到稳定判据。

系统的混合势函数P与其电路结构有关，可根据非线性电路中的电感、电容及非储能元件进行构建，其表达式为

式中：i、v分别为电路中所有电感电流和电容电压构成的向量；iμ、vμ分别为第μ个非储能元件的电流和电压，μ= 1，2，…，b，b为非储能元件的个数；Γ为一维积分曲线，由系统中的电压和电流决定；iσ、vσ分别为第σ个电容的电流和电压。假定一个电路中包含r条电感支路和s条电容支路，且i1,i2,…,ir为所有的电感电流，vr+1,vr+2,…,vr+s为所有的电容电压，则等号右侧第1项为所有非储能元件的电流势，第2项为所有电容的总功率。

混合势函数P的统一形式可表示为

式中：A(i)为电流势函数；B(v)为电压势函数；γ、α为常向量。

定义两个最小特征值μ1、μ2为

式中：λ（·）为矩阵的特征值；L=(L1,L2,…,Lr)为电路中所有电感组成的对角矩阵；C=(C1,C2,…,Cs)为电路中所有电容组成的对角矩阵；Aii(i)为A(i)对i求二阶偏导数；Bvv(v)为B(v)对v求二阶偏导数。

若电路中所有的i和v均满足

且当|i|+|v|→∞时，有

那么当系统受到大信号扰动后，最终还会在趋于稳定的平衡点工作，所以满足式（5）和式（6）的系统，可以保证在大扰动下的稳定性。

3 系统混合势函数方程及稳定性分析

根据混合势函数理论，通过定义支路正方向，确定终端节点和起始节点，以及节点之间的电压差，构造包含系统中所有独立变量i1,i2,…,ir，vr+1,vr+2,…,vr+s的完整网络，从而计算系统支路的能量存储情况，并构建系统的能量函数。在计算时，并不需要采用类似小信号稳定性建模的方法，而是基于从开关周期角度考虑的状态空间平均模型得到系统的混合势函数。因此，针对图2系统的状态平均模型可以进一步分析其在单位周期下的特性，得到适用于混合势函数计算的简单模型。

3.1 源变换器模型简化及系统的混合势函数

当Buck 变换器采用双闭环控制时，可以假设系统电流内环的响应足够快，那么，此时电感电流能够紧紧跟随电压外环的输出电流参考值[19，23]。因此，Buck变换器的状态空间模型可以简化等效为如图3所示的受控电流源和输出电容并联的形式，其中，受控电流源的输出电流等于系统电流内环的参考值。

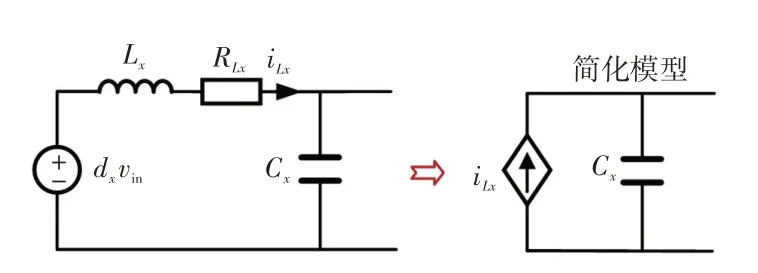
图3 Buck 变换器的简化模型Fig.3 Simplified model of Buck converter

当采用单电压环控制时，不存在电流环，无法直接根据图3对变换器进行简化。因此，需要计算和分析整个系统的混合势函数，进而讨论在单电压环控制下变换器的简化方法。

由图2 的状态空间平均模型，可得基于受控电流源、受控电压源、电阻、CPL等非储能元件建立的电流势函数为

将式（1）代入式（7）可得。

由图2可得系统各电容支路的电压电流乘积为

将式（8）、（9）代入式（2）可得系统混合势函数为

由式（3）给出的混合势函数统一形式，可得电流势函数A（i）和电压势函数B（v）为

由混合势函数定理可得

图4 电感电压电流波形Fig.4 Waveforms of inductor’s voltage and current

三级级联系统的简化大信号模型如图5所示。由于可通过图5 中大信号模型构造混合势函数得到μ1和μ2，因此，图5也可视为系统的通用大信号简化模型。

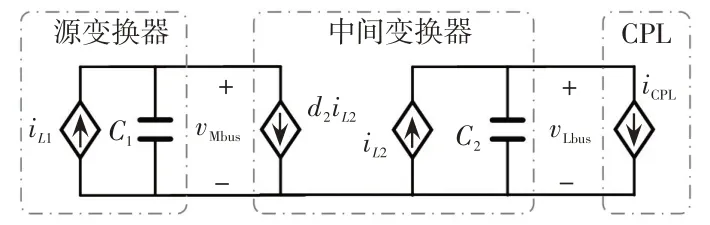
图5 系统通用大信号简化模型Fig.5 General large-signal simplified model of system

为进一步给出系统的大信号稳定判据，将进一步结合系统的不同控制环路求解μ2。

3.2 双闭环控制模式下的大信号稳定判据

当图1所示的三级级联系统采用双闭环PI 控制时，源变换器和中间变换器的控制环路如图6所示，相应的控制环路表达式为

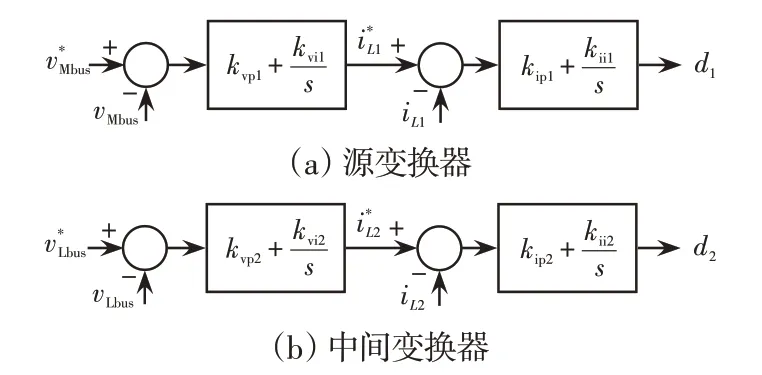
图6 双闭环控制框图Fig.6 Block diagram of double-closed-loop control

由于电流内环相应的速度足够快，内环电流值可以及时的跟随给定值，因此有

由式（14）～（16）可得

将式（17）、（18）代入式（13）可得

忽略变换器损耗，由输入输出功率平衡可得

将式（20）代入式（19）并结合混合势函数理论可以得出，当源变换器和中间变换器均采用双闭环控制时，系统的大信号稳定判据为

由式（21）可知，此时系统的大信号稳定性仅与两个母线电压vMbus和vLbus、源变换器和中间变换器电压外环PI 控制器的比例系数kvp1及kvp2、电容C1和C2，以及负载变换器的功率PCPL有关。

3.3 单电压环控制模式下的大信号稳定判据

当图1 中的三级级联系统采用单电压环控制时，源变换器和中间变换器的控制环路如图7所示，相应的控制环路表达式为

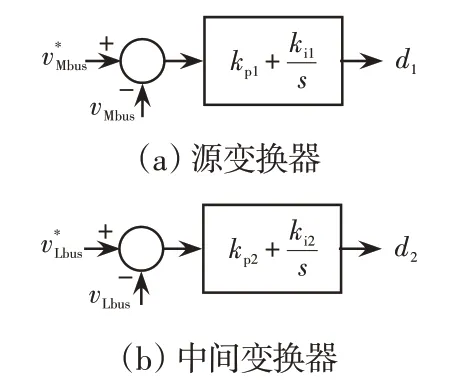
图7 单电压环控制框图Fig.7 Block diagram of single-voltage-loop control

式中：kp1、ki1分别为源变换器的比例和积分系数；kp2、ki2分别为中间变换器的比例和积分系数。

由式（1）可得电感电流iL1和iL2计算式[19]分别为

式中，N1、N2均为常数，不影响偏微分的结果。

于是iL1和iL2对母线电压的偏导数分别为

将式（20）、（26）和式（27）代入式（13）并结合混合势函数理论可以得出，当源变换器和中间变换器均采用单电压环控制时，系统的大信号稳定判据为

由式（28）可知，时系统的大信号稳定性与输入电压vin、母线电压vMbus和vLbus、源变换器和负载变换器PI控制器的比例系数kp1及kp2、电感串联等效电阻RL1和RL2、电容C1和C2，以及负载变换器功率PCPL有关。

对比式（21）与式（28）可以发现，三级级联系统在源变换器和中间变换器采用不同控制方式下得到的大信号稳定判据不同，但均可以图5所示模型构造系统混合势函数的表达式。

4 案例分析与仿真验证

为验证所提出大信号稳定判据的正确性，分别针对采用双闭环控制和单电压环控制的三级级联Buck变换器进行案例分析，并在Matlab/Simulink 仿真平台搭建如图1所示系统的仿真模型进行验证，系统参数如表1所示。其中，系统输入电压为80 V，kvp3、kvi3分别为CPL 电压外环的比例和积分系数；vo为后级变换器输出电压。

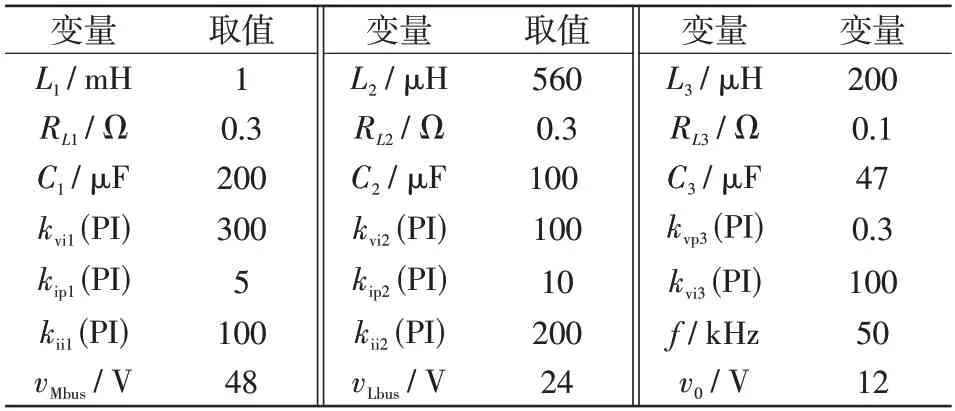
表1 系统参数Tab.1 System parameters

4.1 双闭环控制时系统大信号稳定域分析验证

由式（21）及Matlab 绘制出系统的大信号稳定域如图8所示，并在系统的稳边界上选取两个临界点A1和A2以验证所提系统大信号稳定域的准确性。

图8 系统在双闭环控制下的稳定域Fig.8 Stable region of system under double-closed-loop control

（1）当系统选取临界点A1进行验证时，系统大信号稳定的临界功率为（122÷1.25）W=115 W。设置系统源变换器的电压环比例系数kvp1=0.2，中间变换器的电压环比例系数kvp2=0.2 ，而CPL 将在t=0.4 s 时从96 W 跳变到144 W。由图8 的大信号稳定域可知，CPL 跳变前，系统满足大信号稳定的条件，而跳变后则不满足。图9 给出了系统中2 个母线电压及负载变换器输出电压和电流的仿真波形，其中io为负载电流。由图9可知，在t＜0.4 s时，系统稳定；在t＞0.4 s 时，由于发生负载跳变，系统母线电压产生了振荡。这与由图8 给出的系统大信号稳定域判定结果一致。

图9 负载功率从96 W 切换到144 W 系统仿真波形Fig.9 Simulation waveforms of system when load power is switched from 96 to 144 W

（2）当系统选取临界点A2进行验证时，系统大信号稳定的临界功率为（122÷0.3）W = 480 W。设置系统源变换器的电压环比例系数kvp1=0.2，中间变换器的电压环比例系数kvp2=1.6 ，而CPL 将在t= 0.4 s 时从360 W 跳变到500 W。由图8 的大信号稳定域可知，CPL 跳变前，系统满足大信号稳定的条件，而跳变后则不满足。图10给出了系统中2个母线电压及负载变换器输出电压和电流的仿真波形。由图10可以看出，在t＜0.4 s时，系统稳定；在t＞0.4 s时，由于发生负载跳变，系统母线电压产生了振荡。这与由图9 给出的系统大信号稳定域判定结果一致。

图10 负载功率从360 W 切换到500 W 系统仿真波形Fig.10 Simulation waveforms of system when load power is switched from 360 to 500 W

4.2 单电压环控制时系统大信号稳定域分析验证

在系统采取单闭环控制时，由式（28）及Matlab绘制出系统的大信号稳定域如图11所示，并在系统的稳边界上选取两个临界点A3和A4以验证所提系统大信号稳定域的准确性。

图11 系统在单电压环控制下的稳定域Fig.11 Stable region of system under single-voltage-loop control

（1）当系统选取临界点A3进行验证时，系统大信号稳定的临界功率为（122÷1.3）W = 111 W。设置系统源变换器的电压环比例系数kp1=0.08，中间变换器的电压环比例系数kp2=1.2，而CPL 将在t= 0.2 s 时从144 W 跳变到72 W。由图11 的大信号稳定域可知，CPL 跳变前，系统不满足大信号稳定的条件，而跳变后则满足。图12 给出了系统中2 个母线电压及负载变换器输出电压和电流的仿真波形。由图12 可知，在t＜0.2 s 时，母线电压产生了振荡，系统不稳定；在t＞0.2 s 时，由于发生负载跳变，CPL 减小，系统由不稳定进入稳定状态。这与根据图11中给出的系统大信号稳定域判定结果一致。

图12 负载功率从144 W 切换到72 W 系统仿真波形Fig.12 Simulation waveforms of system when load power is switched from 144 to 72 W

（2）当系统选取临界点A4进行验证时，系统大信号稳定的临界功率为（122÷0.8）W = 180 W。设置系统源变换器的电压环比例系数kp1=0.2，中间变换器的电压环比例系数kp2=1.9，而CPL 将在t=0.2 s 时从288 W 跳变到72 W。由图11 的大信号稳定域可知，CPL 跳变前，系统不满足大信号稳定的条件，而跳变后则满足。图13给出了系统中2个母线电压及负载变换器的输出电压和电流的仿真波形。由图13 可知，在t＜0.2 s 时，母线电压产生了振荡，系统不稳定；在t＞0.2 s 时，由于发生负载跳变，CPL 减小，系统由不稳定进入稳定状态。这与由图11 中给出的系统大信号稳定域判定的结果一致。

图13 负载功率从288 W 切换到72 W 系统仿真波形Fig.13 Simulation waveforms of system when load power is switched from 288 to 72 W

4.3 不同控制模式下系统大信号稳定域的对比

图14 给出了系统在单电压环和双闭环控制方式下的大信号稳定域对比情况。由图14 可知，当不同控制方式下的系统采用相同的源变换器电压环比例系数kvp1和中间变换器的电压环比例系数kvp2时，单电压环控制的大信号稳定域小于双闭环控制下的稳定域；当选取单闭环临界点A5和双闭环临界点A6进行验证时，系统单环控制下大信号临界功率为（122÷0.86）W = 167 W，双闭环控制下大信号临界功率为（122÷0.30）W = 480 W，此时设置kvp1=0.2、kvp2=1.8，而CPL在t=0.2 s时从324 W跳变到180 W，跳变前后系统在单闭环控制下均不满足大信号稳定条件，而系统在双闭环控制下跳变前后均满足大信号稳定条件。

图14 系统在不同控制模式下的稳定域Fig.14 Stable regions of system in different control modes

图15 给出了不同控制环路系统中两个母线电压及负载变换器的输出电压和电流的仿真波形。由图15 可知，在系统切换前后，单环控制下的系统母线电压产生了振荡，系统不稳定；采用双闭环控制时，母线电压在切换前后都处于稳态值，系统处于稳定运行的状态。这与由图14 的判定结果一致。

图15 负载功率从324 W 切换到180 W 系统仿真波形Fig.15 Simulation waveforms of system when load power is switched from 324 to 180 W

5 讨论

5.1 限幅对系统大信号稳定性的影响

实际控制中，对于双闭环控制来说，需对PI 控制器电压外环输出值电感电流进行限幅，以避免超过系统的额定容量[25]。但在大扰动过程中，系统可能工作在限幅工况，这与大信号稳定性分析不同，因此需要进行讨论。

以采用双闭环控制的源变换器为例进行分析，如图16（a）所示。当负载功率PCPL持续增加至电感电流iL1上升到电压外环的最大限幅值IL1_max时，内环PI控制器将变为一个限幅器，其输出恒为IL1_max；同理，当PCPL持续减小至iL1下降到电压外环的最小限幅值IL1_min时，内环输出也是恒定值为IL1_min。显然，工作在限幅工况下源变换器仍然可以等效为电流源与输出滤波电容的并联形式，如图16（b）所示。

图16 限幅工况下的源变换器控制框图与简化模型Fig.16 Control block diagram and simplified model of source converter under limitation working condition

尽管限幅并不改变变换器的大信号简化模型，但其将影响基于混合势函数方法的进一步分析，这是由于当简化模型中的电流源为限幅值IL1_max或IL1_min时，其对系统内其他电气变量的偏导数恒为0。因此，当源变换器或中间变换器工作在限幅工况时，系统大信号稳定判据也将发生变化，具体分析如下。

1）仅源变换器工作在限幅工况

d1=iL1=IL1_max，可得

将式（29）代入式（13）可得

由式（30）可知，μ1+μ2恒小于0，根据混合势函数理论可得出系统恒不稳定。

2）仅中间变换器工作在限幅工况

d2=iL2=IL2_max，可得

将式（31）代入式（13）可得

由式（32）可知，μ1+μ2恒小于0，根据混合势函数理论可得出系统恒不稳定。

3）源变换器和中间变换器均工作在限幅工况

式（29）和式（31）同时成立，因此μ1+μ2恒小于0，系统恒不稳定。

需要说明的是：本节分析结果与文献[26]对两级级联系统的研究结论完全一致。由文献[26]可知，要想三级级联在限幅工况下仍大信号稳定，需要增加一定的阻性负载。

5.2 基于混合势函数的大信号稳定性判据的保守性

尽管本文基于混合势函数给出了系统的大信号稳定域，但这一稳定边界较为保守。以图8中点A1为例进行分析，由所提大信号稳定判据，可得其稳定边界为kvp1=0.2、kvp2=0.2、R=1.25 Ω（对应系统功率115 W），而实际上当R约为1.1 Ω（对应系统功率131 W）时，系统才处于临界稳定状态，两种工况的仿真波形如图17所示。由于点（0.2，0.2，1.25）位于点A1下方，验证了系统大信号稳定域较为保守的结论。

图17 负载功率从115 W 切换到131 W 系统仿真波形Fig.17 Simulation waveforms of system when load power is switched from 115 to 131 W

混合势函数是李雅普诺夫函数的一种特例，其获得的所有稳定性边界均具有保守性的特征，根据这种保守的稳定性准则可以为系统稳定裕度提供足够的保证[19]。文献[27]对比研究了几种大信号稳定评估方案，也证明了基于混合势函数分析方法的保守性。除此之外，导致系统大信号稳定评估结论保守的原因还有寄生参数、建模方法及对CPL过于理想的简化等等，其中，对CPL 的简化处理导致的保守性更为突出[19]。例如，本文直接将CPL 等效为一个受控电流源，而实际变换器的暂态响应与理想的恒功率仍有差距。为此后续工作将进一步研究如何减小所提大信号稳定域的保守性。