计及分布式电源发电出力的自适应反时限保护

方宇辰，王 斌，张良力

（1.武汉科技大学信息科学与工程学院，武汉 430081；2.冶金自动化与检测技术教育部工程研究中心，武汉 430081）

国家《“十四五”现代能源体系规划》[1]提出“积极发展智能电网”的现代化电网建设发展目标，随着新能源发电技术的快速发展，越来越多的分布式电源DG（distributed generation）得到大量应用。由于DG 的大量渗透，整体电网结构由原来单电源辐射型网络转变为多端电源网络，电网发生故障时，故障电流呈双向流动，大小也随之变化[2-4]。由于故障电流受系统结构变化、DG渗透率、发电出力等因素的影响很大，传统保护方式无法满足保护需求，使系统拒动、误动，甚至重合闸失败[5-8]。针对当前系统运行方式与故障特性，需要研究新的电网保护方法[9-11]。目前国内外针对DG 大量接入下的电网保护研究，主要有两个方向：①以通讯系统为基础，集中各保护安装处电气量进行综合判据[12-13]。文献[12]通过IEC61850通讯协议获取保护参数，进而实现自适应电流速断保护；文献[13]通过通信信道接收DG 助增电流大小，保证上、下级保护之间的配合，但该方式存在传输不稳定、抗干扰能力差的缺点。②以传统配网保护为基础，针对故障特性对保护方案进行改进[14-15]。文献[14]提出反时限低阻抗保护方案，利用保护点测量阻抗改进传统反时限过流保护；文献[15]基于DG 助增效应，对反时限方程进行修正。

目前配电网多使用固定整定值的阶段式电流保护，在DG大量接入的情况下，这一方法容易发生误动。反时限保护能够根据保护安装处电气量的大小自动调整动作时限，其本身具备一定应对系统拓扑变化的自适应能力。因此，反时限保护是一种针对新形势下DG 大量渗透，保证系统可靠切除故障的一种有效保护方式。

本文基于传统反时限过流保护动作特性，对电网故障特性和DG影响进行分析，提出一种计及DG发电出力的反时限低阻抗DG-ITLI（distributed generation inverse-time low-impedance）保护方法。利用阻抗修正系数对过渡电阻产生的附加阻抗进行修正，并在阻抗修正系数中，引入电压电流故障偏移角，建立DG 等效阻抗的数学模型，形成以DG 发电出力为影响因子的自适应反时限低阻抗ITLI（inverse-time low-impedance）保护。在MATLAB/Simulink 下建立仿真模型，验证了该保护方案的有效性与可行性。

1 含DG 的电网故障特征

电网中微源大多是以新能源发电单元形式存在的逆变型DG，例如光伏、风机等。不同于传统发电形式，此类微源出力受环境天气与时间的影响很大，极端情况甚至会停止出力或因不可控因素断开与电网的连接。针对不同电网具有不同拓扑结构，接入的DG容量也各不相同，不同DG接入状态与出力对电网保护有着重大影响，因此需要分析DG 对电网保护的影响。首先，建立含DG 的电网结构如图1所示，分析DG1 和DG2 同时接入、DG1 单独接入、DG2 单独接入不同接入状态下的保护动作情况。其中，DG1容量为3 MW；DG2容量为2 MW；ES为系统侧输出电压；EDG1为DG1输出电压；EDG2为DG2输出电压。

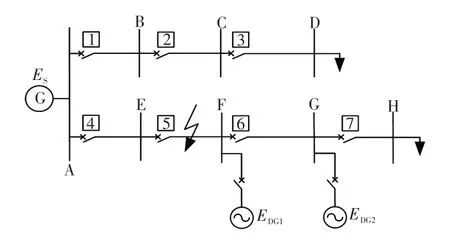
图1 含DG 的电网结构Fig.1 Grid topology with the access of DG

由图1 可知，由于保护5 故障时的故障电流呈双端输入，因此以该段保护为例进行分析。当线路EF 发生三相短路故障时，故障电流由DG1、DG2 与系统侧电源共同提供，由于传统保护为单侧电源下的保护整定，因此DG 的接入将对保护产生影响。通过仿真分析不同接入状态下保护5的动作情况，得出不同DG 接入下保护动作状态如表1所示，其中，“1”表示DG接入系统，“0”表示DG未接入系统。

表1 不同DG 接入下保护动作状态Tab.1 Protection action status with the access of different DGs

由表1 可以看出，当DG1 和DG2 同时接入时，保护能较快地切除故障，满足保护要求；当DG1 或DG2退出时，保护5仍按当前整定值整定，动作时限将产生较大延时，在DG输出功率较低的情况下，甚至会产生拒动。

由此可见故障电流随DG 接入、出力变化而变化，进而对保护的速动性与可靠性产生影响。因此，需要研究一种适合DG 间歇性变化的自适应保护方法来满足系统的保护需求。

2 反时限低阻抗保护原理与整定方法

不同于传统电流保护，反时限保护动作时限随短路电流变化而变化，短路电流越大，动作时间越短。一般反时限过流保护的动作延时方程可表示为

式中：t为保护动作延时；Td为时间整定系数；I为流入保护安装处电流；Iop为保护装置启动电流；A为反时限曲线形状系数；B为曲线平移系数。

当测量电流大于保护装置启动电流时，保护将启动。根据保护原则，要求系统正常运行时保护不动作，相邻线路故障切除后保护返回，因此，对线路时间整定系数Td与启动电流Iop进行整定。

结合图1 电网结构，线路整定首先从距离电源G最远的保护3开始进行整定，即

式中：Iset为电流整定值；Krel为可靠系数；Kss为自启动系数；Kre为电流继电器的返回系数；ILoad.max为正常运行最大负荷电流。

启动电流按式（2）整定为Iop1，对应的动作时间为t1；线路CD 首端短路时，在短路电流IL.max的作用下，保护3 可以整定成固有动作时间tc，由此可得保护3的时限动作特性曲线，从而确定保护安装处的时间整定系数Td与启动电流Iop。对保护2进行整定，其启动电流同理整定为Iop2；在线路BC 首端短路时，为了保证网络的选择性，当短路电流为IL.max时，保护2 可以整定为固有动作时间tb，且必须保证保护2的动作时限比保护3高出一个时间阶梯Δt，即tb=tc+Δt。据此可得保护2 的时限动作特性曲线，从而确定其时间整定系数Td与启动电流Iop。其余保护的动作特性曲线的确定方式与上述保护2、3同理。

根据保护整定原理，将传统反时限过流ITOC（inverse-time over-current）保护和低压反时限保护二者的保护原理相结合，提出ITLI保护。引入阻抗因子Z*的ITLI保护延时方程可表示为

式中：Z*为低阻抗加速因子；Zm为测量阻抗，即短路点到保护安装处的距离；Zline为被保护线路阻抗；m为综合系数，用于调节保护灵敏度。

图2（a）为ITLI保护的动作特性，由图2（a）可以看出，在保护区域内发生故障时，随测量阻抗的减小，即故障电流增大、电压减小，动作时限减小，总体上呈反时限特性。图2（b）为根据ITLI 保护动作特性提取的不同测量阻抗对应的反时限动作曲线，其中，实线为不同测量阻抗下的反时限特性曲线，虚线为发生某一具体线路故障时，根据其测量阻抗选定的反时限特性曲线。ITLI 保护会针对线路故障或系统拓扑结构变化，确定不同线路的测量阻抗，选取对应的反时限动作曲线，并根据其故障电流值，确定故障的切除时限，完成保护整定值的计算和修正，从而实现系统的反时限保护。

图2 不同线路阻抗下ITLI 保护动作特性Fig.2 Action characteristics of ITLI protection under different line impedances

为防止区外故障时阻抗因子Z*过大导致上、下级保护失去配合，对阻抗加速因子Z*分段取值[15]，即

当发生区外故障时，阻抗加速因子Z*恒为1，使区外故障时上、下级线路之间动作延时不变，保证保护的选择性。图3 为ITLI 保护动作延时与短路位置关系曲线，当电网发生区外故障时，由于阻抗因子恒为1，不会使后备保护动作延时增大，同时由于以阻抗因子作为保护动作依据，进而解决了区内短路时靠近系统侧电源保护速动性差的问题。

图3 ITLI 保护动作延时与短路位置关系曲线Fig.3 Curve of relation between ITLI protection action time delay and fault location

3 基于DG 发电出力的DG-ITLI 保护方法

3.1 基于阻抗修正系数的阻抗修正

在第2 节针对反时限保护的分析中，均是以金属性故障为前提进行分析。然而实际系统形成的故障回路中存在由故障电弧形成的过渡电阻，且电弧电阻随电弧不断延伸逐渐增大，使保护处电气量发生变化，最终影响阻抗加速因子Z*的取值。为避免过渡电阻对保护整定产生干扰，利用阻抗修正系数对测量阻抗进行修正，即对过渡电阻产生的附加阻抗进行补偿，保证阻抗加速因子Z*的准确性。

由于过渡电阻的干扰，实际情况下测量阻抗与真实阻抗的关系可表示为

式中：Um为测量电压；Im为测量电流；Uf为故障点电压；If为短路电流；Rg为过渡电阻阻值。

针对故障点两侧存在DG 的双电源系统，分析其故障状态下的电压电流如图4所示。其中，ZS为DG1的等效阻抗；ZDG2为DG2的等效阻抗；ZLine为本段被保护线路阻抗；α为故障位置占比系数；OM为保护点M处测量电压UM；ON为保护点N处测量电压UN；OF为故障点F处测量电压Uf；Rf为故障点故障电阻；IN为N点处测量电流矢量；ψ为偏移角，即测量电流Im与故障点电压Uf之间的夹角；φline为线路阻抗角，即测量电流Im与线路MF 之间的夹角；φui为测量阻抗角，即测量电流Im与测量电压Um之间的夹角。由于故障点两侧DG 电流均流入故障点F，则If=Im+In。

图4 双侧DG 故障下电压、电流分析Fig.4 Voltage and current analysis under dual-side DG fault

以O为原点，作线路MF 的垂线，交MF 延长线于点A，那么MO与AO之间的夹角为φui+90°-φline。垂直点P为保护整定的边界点，如果故障发生在保护范围内，则点P就位于线路MF的延长线上；如果故障发生在保护范围外，则点P就位于线路MF上。MF 为保护安装点M到故障点F的电压差，其值为测量电流Im与短路点到保护安装处的线路阻抗Z的乘积，即|MF|=|ImZ|。在同一故障点发生不同大小过渡电阻故障时，OF在以Uf为弦的圆弧上移动，MF 仍为故障点F到保护安装处线路上的压降U。由此可得各电气量之间的关系为

整理后可得

式中，Z为真实阻抗。

将式（4）、（7）联立可得

式中：ka为阻抗修正系数；ψ为测量电流Im和故障电压Uf的夹角。

由式（6）～（9）可知，对ITLI 保护中的测量阻抗进行修正，需要求得阻抗修正系数ka；对过渡电阻的修正计算，关键在于对故障偏移角ψ的求解。

3.2 基于故障偏移角的阻抗补偿

由于故障点处故障电压Uf和故障电流If同相位，因此偏移角ψ可看作为故障点故障电流If和故障测量电流Im之间的夹角。但实际测量中无法测得故障点故障电流If，因此利用保护安装处电流测量值Im来计算偏移角ψ。

由图4（a）故障下的边界条件可得偏移角ψ为

故障点的负序电流和零序电流可表示为

式中：If2为负序故障电流；If0为零序故障电流；Im2为故障点测量负序电流；Im0为故障点测量零序电流；Cm2为负序电流分配系数；Cm0为零序电流分配系数；ZZ2、ZZ0和ZR2、ZR0分别为故障点上游线路负序阻抗、零序阻抗和下游线路负序阻抗、零序阻抗；ZL2为线路负序阻抗；ZL0为线路零序阻抗；α为故障位置占比系数。

在传统配网中，一般将负序电流分配系数和零序电流分配系数作为常数。但在DG大量渗透的情况下，由式（11）可得，负序、零序电流分配系数受DG 等效阻抗影响很大，不再适合作为常数。因此基于电流分配系数，根据图4双侧DG的电压、电流关系，建立故障偏移角ψ与DG 等效阻抗XN之间的等效拓扑如图5所示。其中，ZM为M侧DG等效阻抗；ZN为N侧DG 等效阻抗；y为故障点至M侧线路总长；l为MN线路总长；ΔIM为M侧DG 所产生的电流偏移量；ΔIN为N侧DG 所产生的电流偏移量；ΔIf为故障点的电流偏移量；Rf为故障点电阻；rL为单位长度线路阻抗。

图5 含DG 系统故障分量等效拓扑Fig.5 Equivalent topology of system fault components with DG

基于故障时电压电流向量的关系，对偏移角ψ进行分析，可得

式中：U为DG 输出电压；XM为M侧DG 的等效电抗；XN为N侧DG的等效电抗；XL为单位线路的等效电抗；rL为单位长度线路阻抗；δ为ΔIf和ΔIm的夹角。

由式（13）可知，偏移角ψ受M、N两侧DG 阻抗影响，并随DG等效阻抗XM、XN实时变换。

3.3 基于DG 发电出力的DG-ITLI 保护整定

在第3.2 节中已建立保护动作时限与DG 等效阻抗的关系模型，但DG间歇性特点具体体现在DG出力的实时变化而非其等效阻抗变化，因此需在保护动作与DG发电出力间建立关系模型。以光伏微源为例，根据其发电出力特性建立光伏发电出力P与其等效阻抗XN的关系模型。将系统短路时最大可升高电压与最大可升高电流之比来近似表示微源等效阻抗，分析不同功率等级发电出力P与其对应等效阻抗XN的关系，并根据发电出力P与等效阻抗XN之间的对应关系进行拟合，得到二者的关系呈幂函数形式如图6所示。

图6 等效阻抗与光伏出力拟合曲线Fig.6 Fitting curve of equivalent resistance and photovoltaic output

设XN=F(P)=aPb，利用最小二乘法确定P与XN之间的关系，设函数G为

式中：a、b均为拟合系数；P为DG发电出力大小；Xi为第i个光伏点阻抗大小，i=1，2，…，n，n为曲线拟合数据的数量；Pi为第i个光伏点发电出力大小。

对函数G分别求a和b的偏导可得

将图2 各点数据带入，可得光伏发电出力P与等效阻抗XN满足的幂函数关系为

将式（3）、（7）、（9）、（13）、（16）联立可形成DGITLI保护的判别整定依据为

根据式（16）发电出力P与等效阻抗XN的关系，可得发电出力的实时变化影响其等效阻抗实时变化，进而影响式（13）中故障偏移角ψ的变换；故障偏移角ψ与阻抗修正系数ka有关，通过对阻抗系数的修正，能较大程度地降低过渡电阻的干扰，从而保证式（4）中阻抗加速因子Z*的准确性，进而保证DG-ITLI保护的速动性与选择性。

4 仿真验证

4.1 电网结构及相应参数

基于第3.1～3.3节理论分析，以光伏DG作为微源，搭建如图7所示的电网结构拓扑，详细对比分析ITOC 保护、低压ITOC（UA-ITOC）保护、传统低阻抗ITOC（ZA-ITOC）保护、改进低阻抗ITOC（IZA-ITOC）保护、DG-ITLI 保护动作时限与上、下级保护配合的能力。其中，系统电压等级为10 kV，DG 均为逆变型微源，容量为5 MW，通过不同百分比发电出力改变其输出功率；最大输出电流为额定电流的2倍，DG均采用恒功率控制方式且考虑其低压穿越作用的影响；上、下级线路保护时间阶梯Δt=0.5 s ；配网等效阻抗ZS=j0.5 Ω 、z=0.210+j0.287 Ω/km，线路长度均为10 km，配置均为反时限保护。

图7 电网系统结构Fig.7 Structure of grid system

（1）对无DG接入三相短路情况下，各保护的保护效果进行对比分析。线路AB段短路，保护1 动作，保护延时情况如表2所示。由表2可以看出，保护1 由于靠近电源侧，ITOC 保护动作延时较长，动作速度较慢；UA-ITOC保护与ZA-ITOC保护有一定程度的加速效果，但不够明显；IZA-ITOC 保护与DG-ITLI保护动作延时最短，动作速度最快，能最大程度满足保护速动性。在DG-ITLI保护下末端保护出口处的故障电压、电流波形如图8、9所示。由图8、9 波形可以看出，当0.2 s 发生故障后，经由DGITLI 保护判据并快速动作，将故障切除，系统恢复运行。故DG-ITLI 保护的动作较其他保护更加迅速，保证了保护的速动性。

表2 线路AB 短路保护延时Tab.2 Protection time delay under short-circuit fault condition at Line AB s

图8 DG-ITLI 保护下故障电压波形Fig.8 Fault voltage waveform under DG-ITLI protection

图9 DG-ITLI 保护下故障电流波形Fig.9 Fault current waveform under DG-ITLI protection

（2）线路CD段短路，保护1、2、3 均动作，其动作延时如表3所示。由表3 可以看出，在UA-ITOC下保护2 与保护3 时间阶梯Δt＜0.5 s，不满足保护配合时限；而DG-ITLI能够有效保证上、下级时间阶梯，保证系统的选择性；在速动性与可靠性方面，DG-ITLI相比传统保护，更加迅速与可靠，并能较好地满足上、下级保护的故障处理。

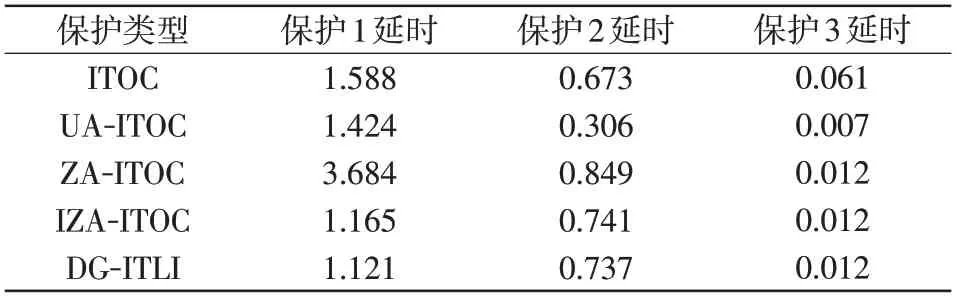
表3 线路CD 短路保护延时Tab.3 Protection time delay under short-circuit fault condition at Line CDs

4.2 阻抗加速因子补偿可靠性仿真结果分析

表4 DG 相邻线路AB 短路时保护动作延时Tab.4 Protection action time delay under short-circuit fault condition at Line AB which is adjacent to DGs

4.3 过渡电阻抗扰仿真结果分析

针对电网发生故障情况后，线路过渡电阻从0开始逐渐变化，持续对测量阻抗产生干扰的情况，来验证在过渡电阻干扰下，各保护方案能否保证故障可靠切除。将DG1、DG2 分别接入母线E、F，线路EF故障时，对比不同过渡电阻对各保护的影响，其结果如表5所示。

表5 经不同过渡电阻线路EF 短路时保护动作时间Tab.5 Protection action time under short-circuit fault condition at Line EF with different transition resistancess

由表5可以看出，ITOC保护随过渡电阻增加动作延时严重，基本没有过渡电阻抗扰能力，保护的速动性与上、下级保护配合均受到较大影响；IZAITLI保护在过渡电阻较小时，一定程度上能够保证保护的速动性，但随着过渡电阻增大，由于其无法进行阻抗修正，故障偏移角ψ逐渐增大，上、下级保护的时间阶梯也逐渐偏移，与式（7）理论分析一致；DG-ITLI保护由于引入阻抗修正系数ka，对测量阻抗进行修正，最大限度补偿因过渡电阻产生的附加阻抗，在满足保护速动性的前提下，还能较好的保证上、下级线路的保护配合关系，且在高阻故障状态下，仍具有较好的动作特性。

4.4 DG 间歇发电出力抗性仿真结果分析

针对DG大量接入电网并间歇性频繁变换的特性，分析在不同出力DG 接入下各保护的可靠性。将DG3 接入母线H，线路HI故障时，不同出力DG3对各保护影响，具体对比DG3 出力为10%、20%、50%、80%和100%的情况下，线路HI短路保护动作时限如表6所示。

表6 不同DG 出力下线路HI 短路保护动作时限Tab.6 Protection action time under short-circuit fault condition at Line HI with different DG output s

由表6可以看出，随着DG出力减小，其等效阻抗XN增大，过渡电阻影响减小，DG 提供的故障电流逐渐减小，致使保护7 与保护8 的动作时间差逐渐减小。当DG出力为20%时，ITOC与IZA-ITOC保护动作时限差小于标准时间阶梯Δt，可能造成保护误动，降低保护的可靠性；而DG-ITLI 保护针对DG出力变化时保护点故障电流、电压的不同，选择不同反时限动作特性曲线，形成针对DG 出力变化的自适应保护方案，保证保护可靠性；即使在DG出力仅为10%的情况下，上、下级保护时限仍然维持在标准时间阶梯Δt下，保证保护的选择性；而在其余出力情况下，DG-ITLI 保护也具备良好的速动与选择能力。

为验证在ITLI和DG-ITLI保护下线路保护选择性效果，调节DG 为100%、80%、60%、50%出力，线路每500 m 处设置三相短路故障，分析DG 的助增效应对ITOC保护选择性的影响，将不同DG发电出力的离散点数据进行拟合形成曲线如图10所示。

图10 不同DG 发电出力下ITLI 保护的时间阶梯Fig.10 ITLI protection time steps under different DG output

由图10可以看出，在DG出力为100%的情况下，DG 的助增效应对线路保护产生的影响最大，故障点由保护出口处向保护末端移动的过程中，保护7与保护8之间的时间阶梯逐渐减小至负数，保护逐渐失去选择性；在DG 出力为80%的情况下，DG 的助增效果相对减弱，选择性失配点(Δt78＜0)相较于100%出力下向线路后端移动，但保护依旧会失去选择性。

通过对比可以发现，DG的发电出力越大，其助增效应越明显，对传统线路保护的影响越大，甚至导致其失去选择性。

在相同故障条件下，对DG-ITLI 保护的选择效果进行仿真验证，将不同DG 发电出力的离散点数据进行拟合形成曲线如图11所示。

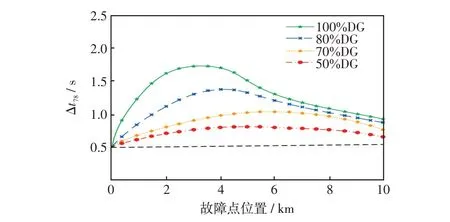
图11 不同DG 发电出力下DG-ITLI 保护的时间阶梯Fig.11 DG-ITLI protection time steps under different DG output

由图11 可以看出，由于DG-ITLI 保护通过DG出力对阻抗修正因子进行自适应修正，实现了对反时限动作曲线的优化，能准确地反应线路各处的故障，在不同DG出力的情况下均可以保证上、下级的保护配合；且在保证保护上、下级配合关系的前提下，能够最大程度保证保护快速动作，确保全线保护的速动性与选择性。

综上仿真结果可以看出，DG-ITLI 保护针对不同DG 出力采用特定反时限特性曲线，以保护速动性为最优前提，同时尽量保证上、下级保护之间的保护配合；DG-ITLI保护以阻抗参数作为保护依据，使保护具有距离保护的优越性，能够反应故障距离，不受系统运行方式和故障类型的影响，即使在被保护线路末端发生故障，仍能以较快的速度动作。

5 结论

本文针对DG发电出力间歇性变化对电力系统继电保护的影响，提出一种基于DG 出力变化的自适应反时限低阻抗保护方法，该方法针对DG 的发电出力特性，利用故障偏移角与阻抗修正系数补偿附加阻抗，通过DG 出力状态选择合适的反时限特性曲线和动作时间常数，进而完成ITLI保护定值的自适应整定。该方案具有以下特点：

（1）当被保护线路发生区外故障时，利用阻抗加速因子分段取值，保证了保护的选择性；

（2）该保护方案具有较好的抗过渡电阻能力，在高阻故障状态下，仍具有较好的动作特性，保证了保护的速动性；

（3）该保护方案能自适应根据DG 发电出力选择动作曲线，不需要随DG间歇性变换切换整定值，进一步提高了自适应保护的性能。