单钢板混凝土组合板冲击响应的数值模拟及计算方法
2023-10-31赵唯以庞庆宏
赵唯以, 庞庆宏
(青岛理工大学 土木工程学院,山东 青岛 266033)
钢板-混凝土组合(steel plate-concrete composite structures,SC)结构是由外侧钢板(单侧或双侧)、剪力连接件和混凝土组合而成的一种新型结构[1-2]。在工程中,剪力墙等抗侧力构件可以采用双钢板-混凝土组合结构(Full-SC),而楼板、桥面板等受弯构件则可采用单钢板-混凝土组合结构(Half-SC)。典型的SC结构如图1所示。
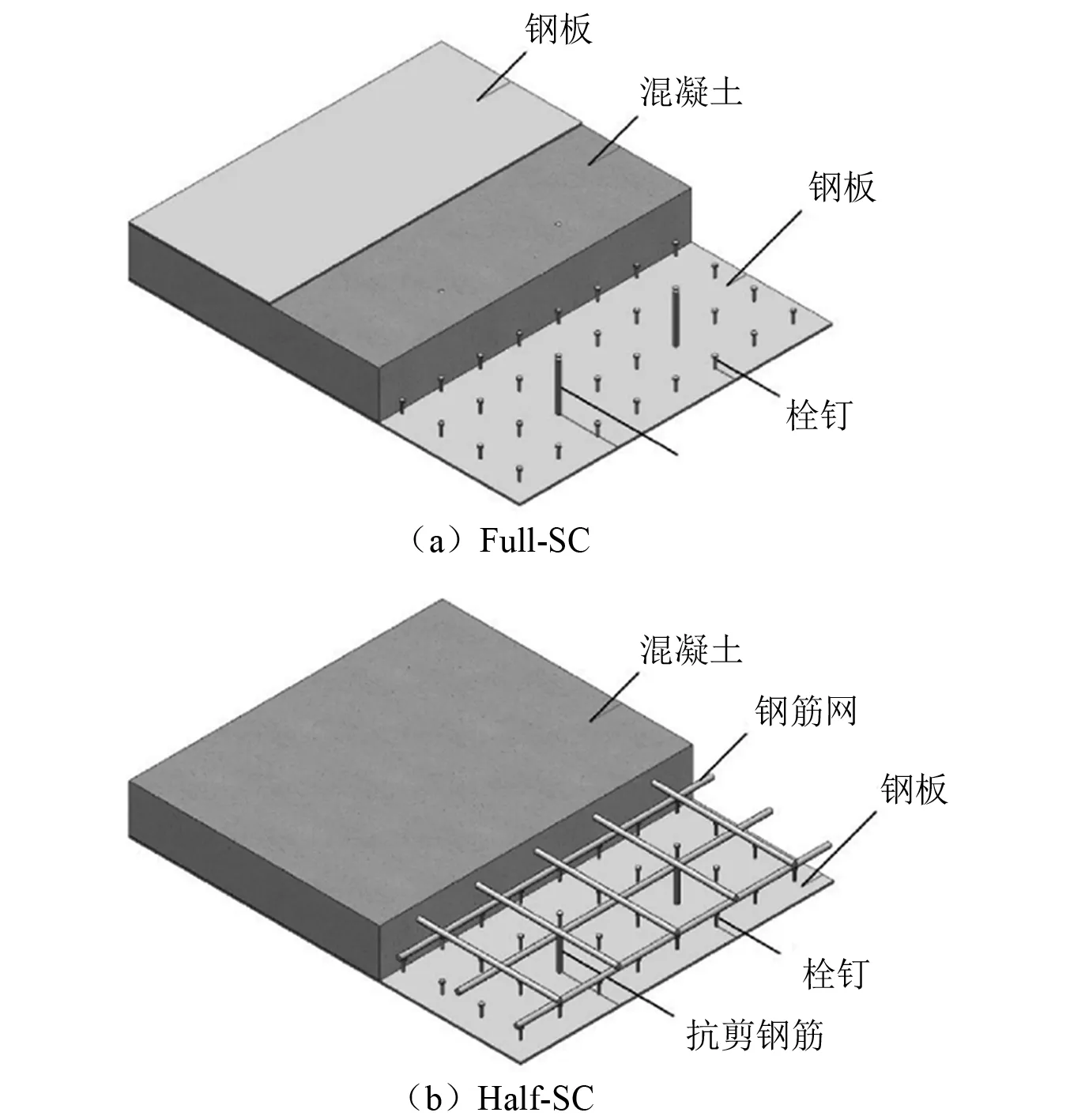
图1 典型的SC结构形式
结构在投入使用阶段除承担正常的恒、活荷载外,还可能会受到意外冲击作用的威胁。在SC结构的设计中如未充分考虑冲击作用的影响,可能会造成严重的人员伤亡和财产损失。Half-SC板作为一种新型组合结构,在桥梁、核电站、高层建筑等重要基础设施中得到了广泛应用。因此,进行Half-SC板的动力响应和抗冲击性能研究,对于保证结构物的安全性能具有重要意义。
针对Half-SC板在弹道冲击下的侵彻或贯穿破坏问题,Walter等[3-7]开展了高速冲击试验,结果均表明在背部设置钢板可以有效提高结构的抗冲击性能,而在受冲击侧设置钢板的作用较小。由于计算混凝土结构侵彻和贯穿的经验公式相对成熟,Walter等和Tsubota等将钢板等效为混凝土,并提出了等效厚度计算公式。Grisaro等[8]则在Walter试验结果的基础上,修正了混凝土结构的穿透公式,使之可以考虑钢板的影响。Bruhl等[9]汇总了已有的Full-SC板和Half-SC板高速冲击试验结果,并同时采纳了混凝土和钢板两种结构的穿透公式,提出了防止SC结构贯穿的三步设计法,该方法已被美国ANSI/AISC N690s1-15规范[10]推荐使用。
在大质量低速度的冲击作用下,Half-SC板的整体变形响应也是设计中需要关注的重点。然而,这方面的研究相对较少。窦旭强[11]进行了1片Half-SC板的静力加载试验和5片Half-SC板的落锤冲击试验,结果表明板底最大位移与冲击能量基本呈线性关系。赵唯以等[12]基于有限元模拟和机器学习算法训练了Half-SC板在落石冲击下最大变形的预测模型,但缺乏准确的力学模型且适用范围有限。
为了进一步揭示Half-SC板在冲击作用下的力学性能和动力响应过程,本文基于LS-DYNA对现有Half-SC板的落锤冲击试验开展数值模拟,并分析冲击物质量、冲击速度和钢板厚度等参数对Half-SC板动力响应的影响规律。在此基础上,推导Half-SC板的抗力和刚度计算式,提出Half-SC板的抗力函数模型,并合理考虑材料的应变率效应,最终建立计算Half-SC板变形响应时程的等效单自由度模型。
1 有限元分析
1.1 现有试验研究
窦旭强开展了1片Half-SC板的静力加载试验和5片Half-SC板的落锤冲击试验。试件的具体结构形式如图2所示,所有试件长1 000 mm、宽1 000 mm,底面钢板厚2 mm,混凝土厚75 mm。试件内布置栓钉、抗剪钢筋和钢筋网,均与钢板焊接连接。其中,栓钉的直径为5 mm,长度为20 mm,间距为50 mm;抗剪钢筋采用直径6 mm光圆钢筋,布置间距为150 mm;钢筋网采用直径为10 mm的HRB335级钢筋,双向布置,同向钢筋间距为75 mm,混凝土保护层厚度为15 mm。为了在试验时用高强螺栓固定试件位置,在试件上用直径50 mm的钢管预留了8个孔洞。具体材料性能如表1和表2所示。
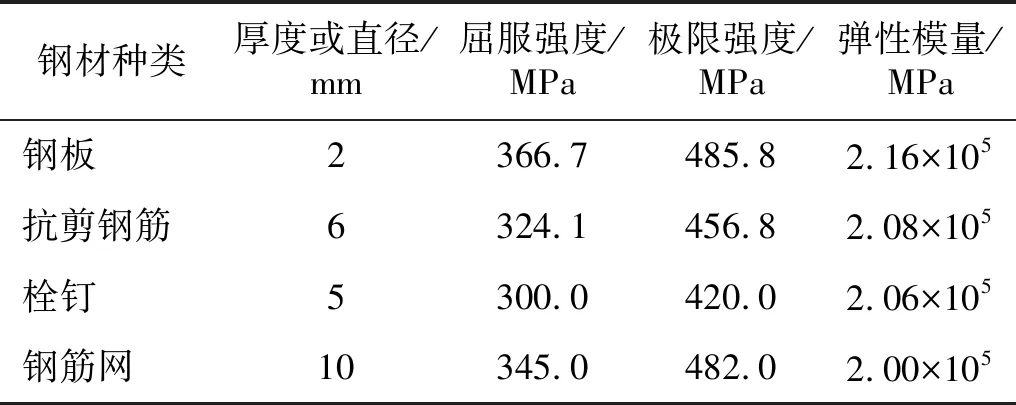
表1 钢材材料性能

表2 混凝土材料性能
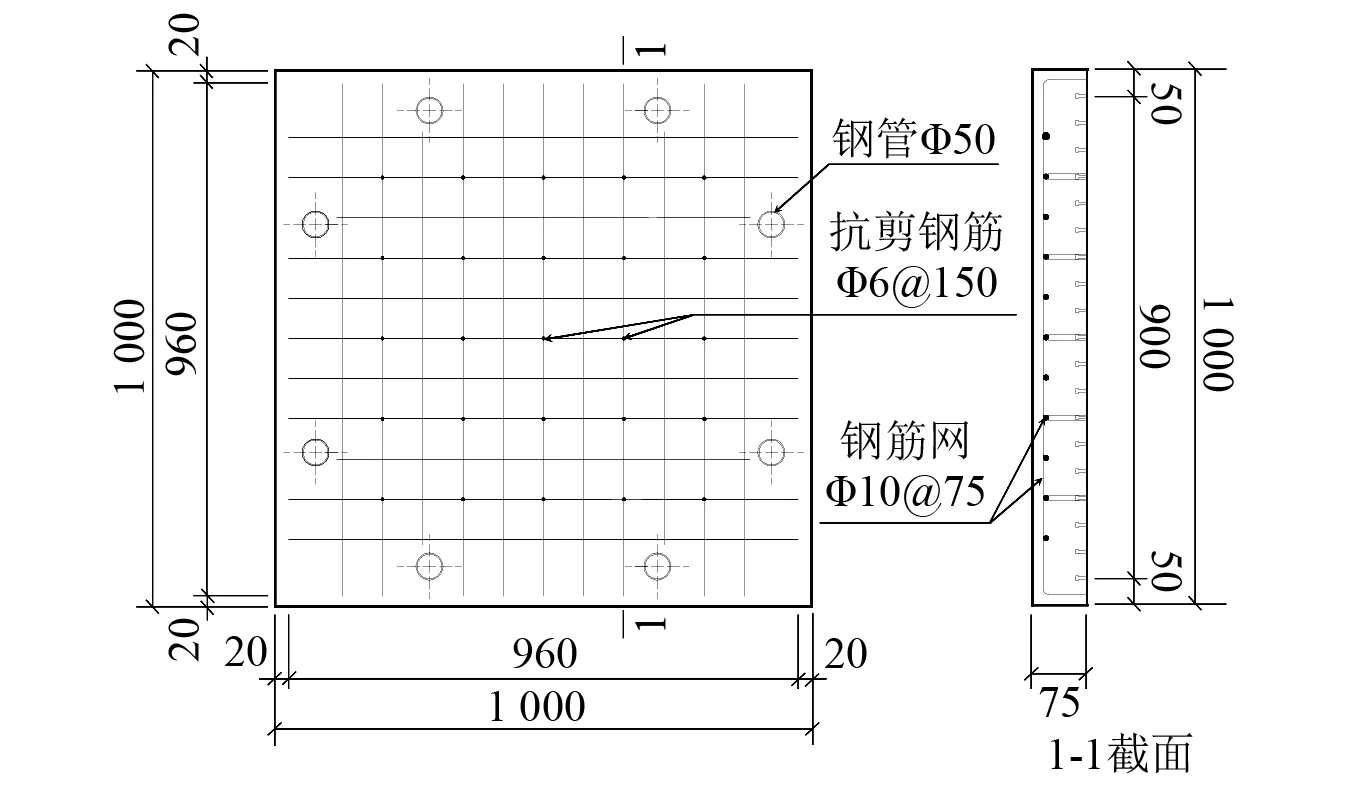
图2 Half-SC板试件加工图(mm)
在静力试验和冲击试验中,试件所受边界条件为四边简支,双向跨度为750 mm。静力加载使用正方形平板加载,边长为150 mm。冲击试验所使用的落锤由冲击头、力传感器和配重三部分组成,各部分之间通过高强螺栓连接,落锤总质量为660 kg,冲击头直径为80 mm。为了研究Half-SC板在不同冲击能量下的动力响应,选取0.5 m,1.0 m,1.5 m,2.0 m,2.5 m共5个落锤释放高度进行面外落锤冲击试验。试验中记录了Half-SC板底中心的位移时程和冲击力时程,具体结果如表3所示。其中,试件编号由字母H和落锤落距组成,如H05即落锤释放高度为0.5 m的试件。

表3 试验主要参数和结果
1.2 有限元模型建立
1.2.1 单元与网格
针对上述试验研究,本文采用LS-DYNA开展数值模拟和参数分析。基于LS-PrePost前处理软件建立Half-SC板有限元模型,如图3所示。其中,抗剪钢筋、栓钉和钢筋网采用 Hughes-Liu with cross section integration beam梁单元(ELFORM=1);钢板、混凝土、支座和落锤均采用 constant stress solid实体单元(ELFORM=1)。通过收敛性研究,确定冲击点和抗剪钢筋区域的网格尺寸为12.5 mm,其他区域网格尺寸为25 mm,以节省计算时间且不损失精度。
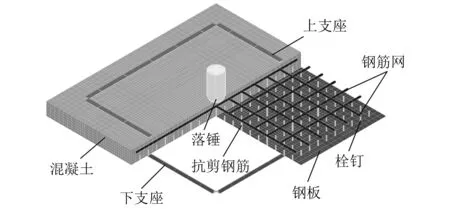
图3 有限元模型剖切视图
1.2.2 边界与约束
定义关键字*BOUNDARY_SPC_SET以约束上下支座所有节点的平动自由度,使其位置完全固定。落锤位置紧贴混凝土,定义关键字*INITIAL_VELOCITY_GENERATION对落锤施加接触Half-SC板瞬间的初速度。混凝土与钢筋网、栓钉以及抗剪钢筋之间保证共节点连接。
在落锤与混凝土、落锤与钢板、混凝土与钢板以及钢板与支座之间,定义自动面面接触(AUTOMATIC_SURFACE_TO_SURFACE)。其中钢板与混凝土之间的静摩擦因数取0.3,动摩擦因数取0.1,不考虑黏结作用;忽略落锤与试件之间的摩擦[13]。
1.2.3 材料本构
本文有限元模型中选取的材料本构如下:
(1) 钢材(钢板、栓钉、抗剪钢筋和钢筋网)均选用*MAT_003(*MAT_PLASTIC_KINEMATIC)本构模型。该模型定义了双线型应力-应变关系,输入参数包括屈服应力、弹性模量、切线模量、硬化参数和失效应变等。采用Cowper-Symonds模型考虑钢材的应变率效应,如式(1)所示
(1)
式中:σd为钢材在应变率为ε时的屈服强度;σs为静力条件下钢材的屈服强度;系数D取40.4 s-1,q取5[14]。钢材的失效应变FS取0.35。
(2)混凝土采用*MAT_159(*MAT_CSCM)模型。该模型可以有效地预测结构在低速冲击载荷下的性能,输入参数包括混凝土棱柱体抗压强度、密度和骨料粒径等。模型中率效应开关打开(即IRATE=1)以考虑应变率效应的影响。
(3) 对于支座和落锤,因为在冲击过程中仅发生弹性变形而选用*MAT_20(*MAT_RIGID)刚体本构模型进行模拟,以节省计算时间。模型所需的参数参考标准低碳钢的材性,弹性模量取2.06×105MPa,密度取7.8×10-9/mm3。由于落锤模型的体积与实际情况不同,因此通过改变密度使其质量与实际相同。
1.2.4 沙漏控制
定义关键字HOURGLASS对钢板和混凝土进行沙漏控制以减少沙漏效应,采用IHQ=6(Belytschko-Bindeman strain co-rotational stiffness form)沙漏控制,沙漏系数QH取0.03。
1.3 模型验证
5片Half-SC板试件的下表面中心位移时程(w-t)曲线,如图4所示。由于试验中出现意外情况,试件H15的下表面中心位移时程数据缺失。由图4可知,随着冲击能量的增大,试件下表面中心位移峰值变大,到达峰值的时间增加。通过对比发现模拟结果和试验曲线吻合良好。
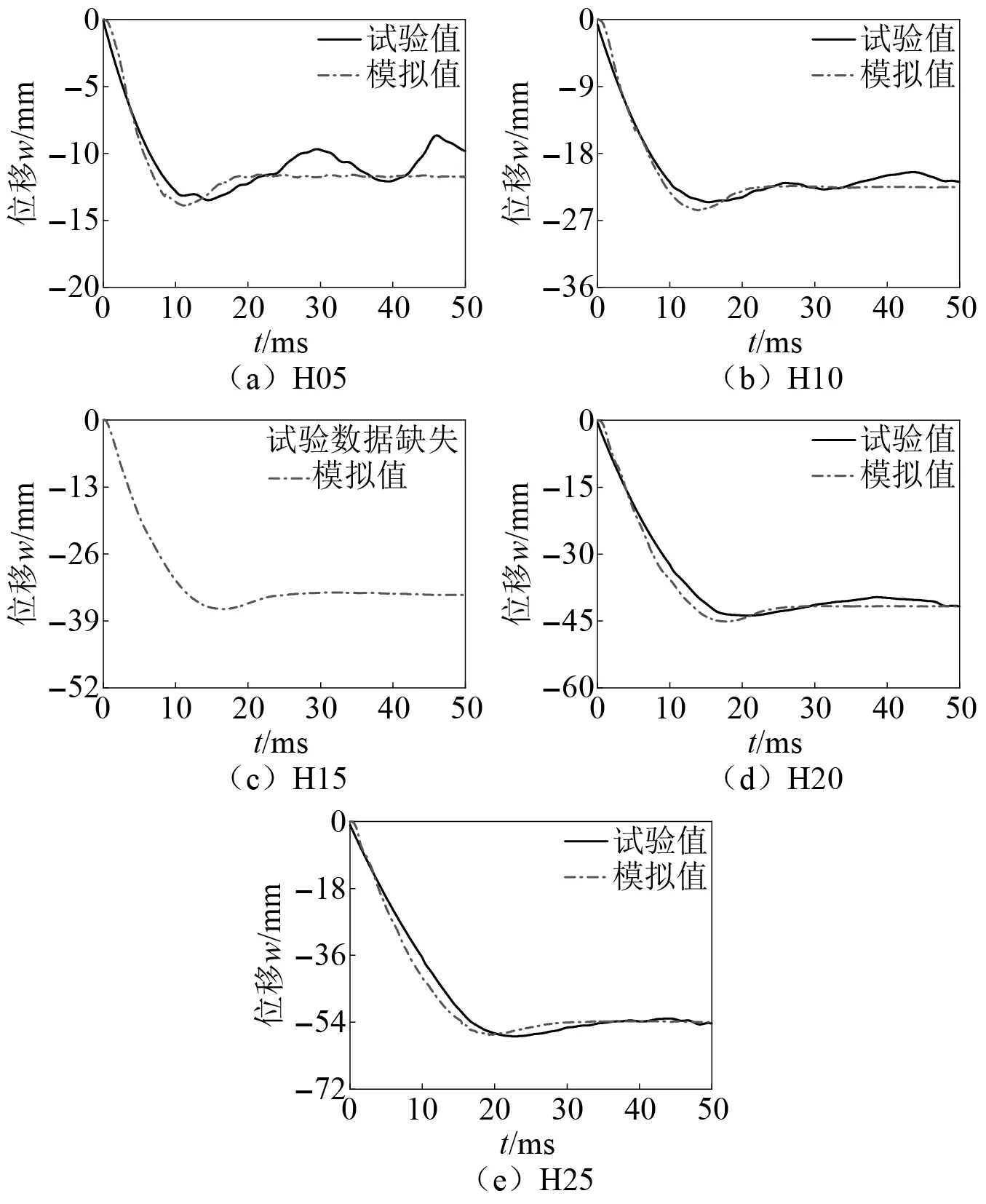
图4 板底中心位移时程曲线
5片Half-SC板的冲击力时程(F-t)曲线,如图5所示。在落锤与Half-SC板发生接触后,冲击力在极短时间内到达惯性响应阶段的冲击力峰值,该阶段的冲击力峰值主要与冲击质量、落锤和试件之间的接触刚度和冲击速度有关[15]。达到该峰值后,由于落锤与试件之间的分离趋势,冲击力有所下降。随后试件承载力进入强化段,冲击力再次提高。当冲击能量全部转化为变形能时,落锤开始回弹,冲击力逐渐下降最终变为零。
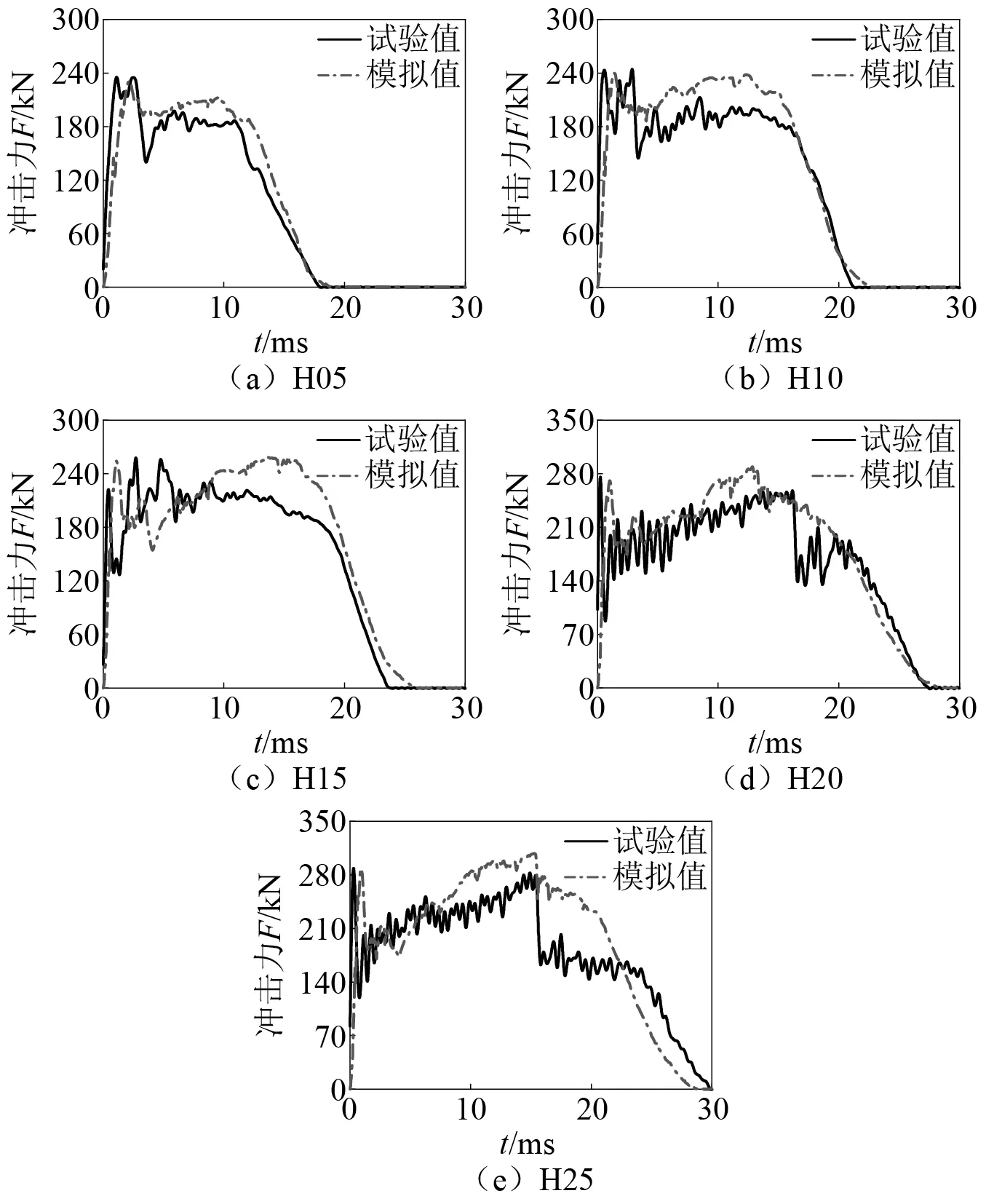
图5 冲击力时程曲线
试件H20和试件H25的冲击力分别在16 ms和15 ms时发生骤降,分析原因是钢筋发生断裂导致冲击力部分卸载,模拟结果中钢筋网同样出现断裂,但发生时间相比试验略有提前。由图5可知,随着冲击能量的增大,冲击力峰值提高,持续时间增加。模拟结果与试验结果整体趋势吻合较好。
各试件达到最大变形时的竖向位移等值线,如图6所示。由图6可知,Half-SC板的变形由整体弯曲变形和局部冲切变形组成。冲击后的试件H15跨中剖切图与有限元模型变形结果对比,如图7所示。有限元模型受冲击后形成冲切锥体的直径约为300 mm,与试验结果基本吻合。试验过程中,试件H25出现了钢板撕裂现象,有限元模型对该现象进行了很好的模拟,如图8所示。由图7、图8可知,有限元模型可以有效预测Half-SC板的整体和局部变形。

图8 试件H25底部钢板局部撕裂
2 参数分析
基于本文建立的有限元模型,本章分别参数化研究了冲击物质量、冲击速度和钢板厚度3个参数对Half-SC板冲击响应的影响规律,选取板底中心位移作为Half-SC板冲击响应的关键指标。标准试件钢板厚度为4 mm,冲击物质量为400 kg,冲击速度为5 m/s,分析单一参数影响时保持其他参数不变。
2.1 冲击物质量
图9和图10给出了当冲击物质量分别为100 kg,200 kg,300 kg,400 kg,500 kg,600 kg,700 kg和800 kg时,Half-SC板的板底中心位移时程曲线以及最大位移和残余位移。结果表明,随着冲击物质量的增加,对应的板底中心最大位移分别为7.4 mm,13.0 mm,17.1 mm,20.5 mm,23.5 mm,26.8 mm,29.8 mm和32.3 mm,残余位移分别为6.2 mm,11.2 mm,15.4 mm,18.6 mm,21.3 mm,24.5 mm,27.3 mm和29.7 mm,最大位移和残余位移均呈上升趋势。由图10可知,位移与冲击物质量近似呈线性关系。
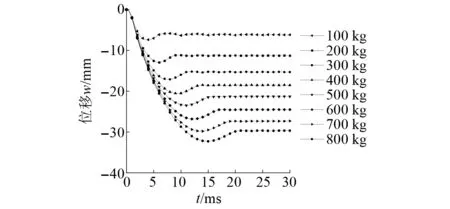
图9 不同冲击物质量下板底中心位移时程曲线
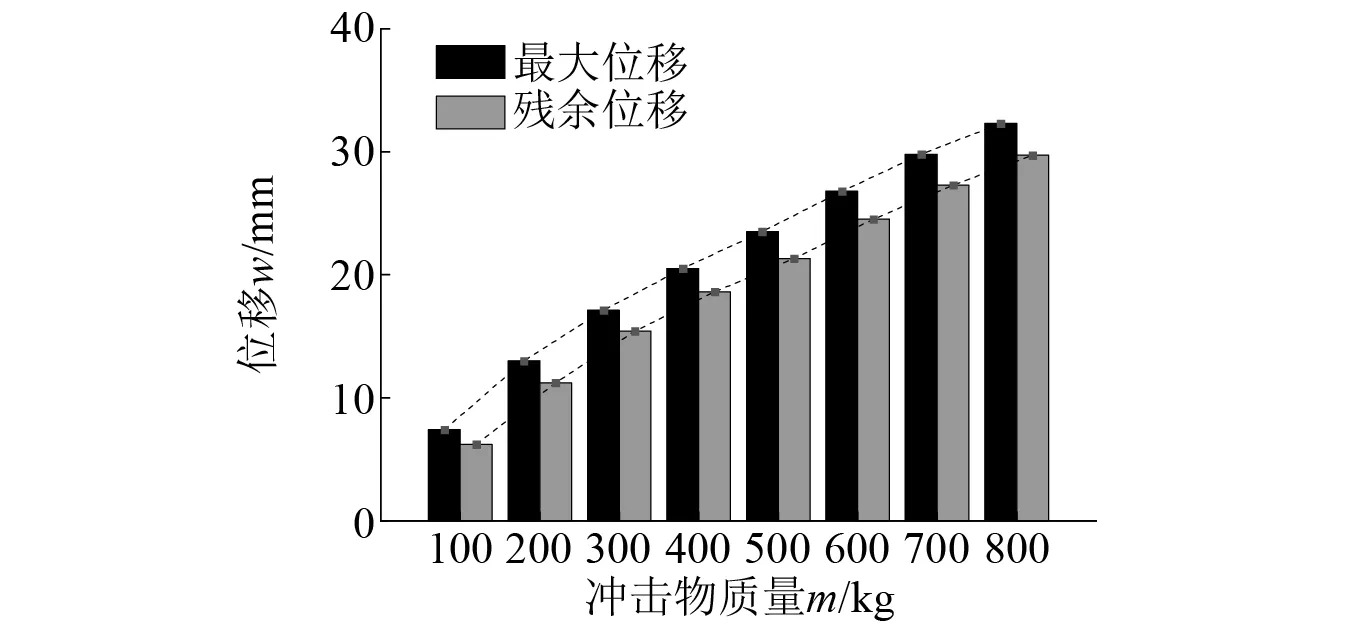
图10 不同冲击物质量下板底最大位移及残余位移
2.2 冲击速度
图11和图12给出了当冲击速度分别为2 m/s,3 m/s,4 m/s,5 m/s,6 m/s,7 m/s,8 m/s和9 m/s时,Half-SC板的板底中心位移时程曲线以及最大位移和残余位移。由图可知,随着冲击速度的提升,对应的板底中心最大位移分别为6.2 mm,10.7 mm,15.4 mm,20.5 mm,25.9 mm,31.4 mm,35.8 mm和39.7 mm,残余位移分别为5.1 mm,9.2 mm,13.7 mm,18.5 mm,23.7 mm,29.0 mm,33.2 mm和36.5 mm,最大位移和残余位移均呈增长趋势。由图12可知,位移与冲击速度近似呈线性关系。
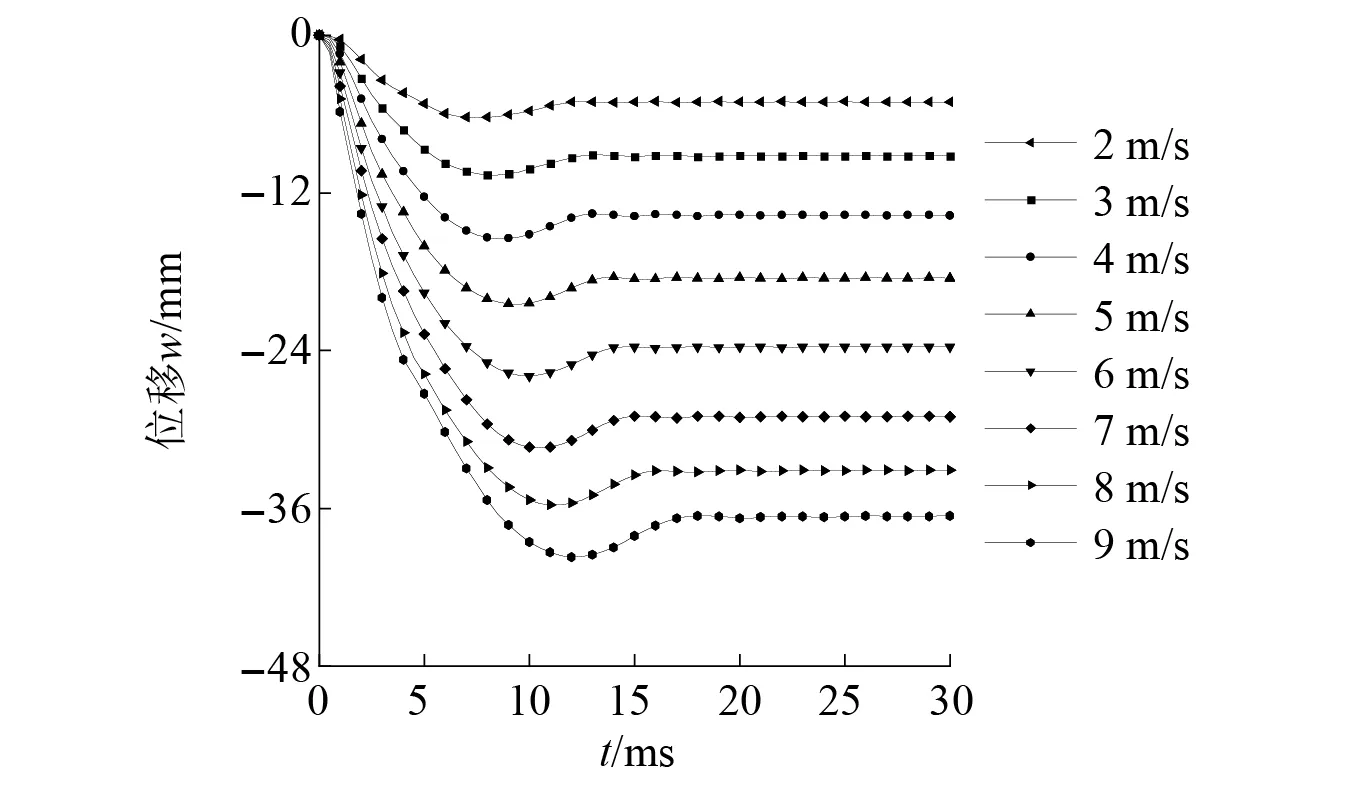
图11 不同冲击速度下板底中心位移时程曲线
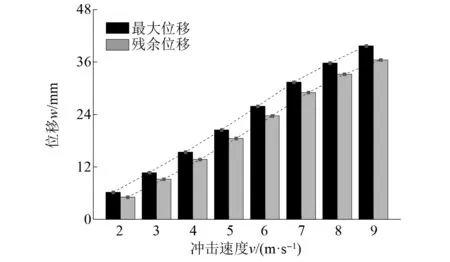
图12 不同冲击速度下板底最大位移及残余位移
2.3 钢板厚度
图13和图14给出了当钢板厚度分别为1 mm,2 mm,3 mm,4 mm,5 mm,6 mm,7 mm和8 mm时,Half-SC板的板底中心位移时程曲线以及最大位移和残余位移。结果表明,随着钢板厚度的增加,对应的板底中心最大位移分别为26.2 mm,24.2 mm,22.3 mm,20.7 mm,19.8 mm,19.1 mm,18.5 mm和17.5 mm,残余位移分别为24.6 mm,22.2 mm,20.2 mm,18.6 mm,17.7 mm,17.0 mm,16.3 mm和15.2 mm,最大位移和残余位移均呈下降趋势。由图14可知,位移与钢板厚度近似呈线性关系。增加钢板厚度,可以提高Half-SC板的刚度和承载力,从而减小板的冲击响应。
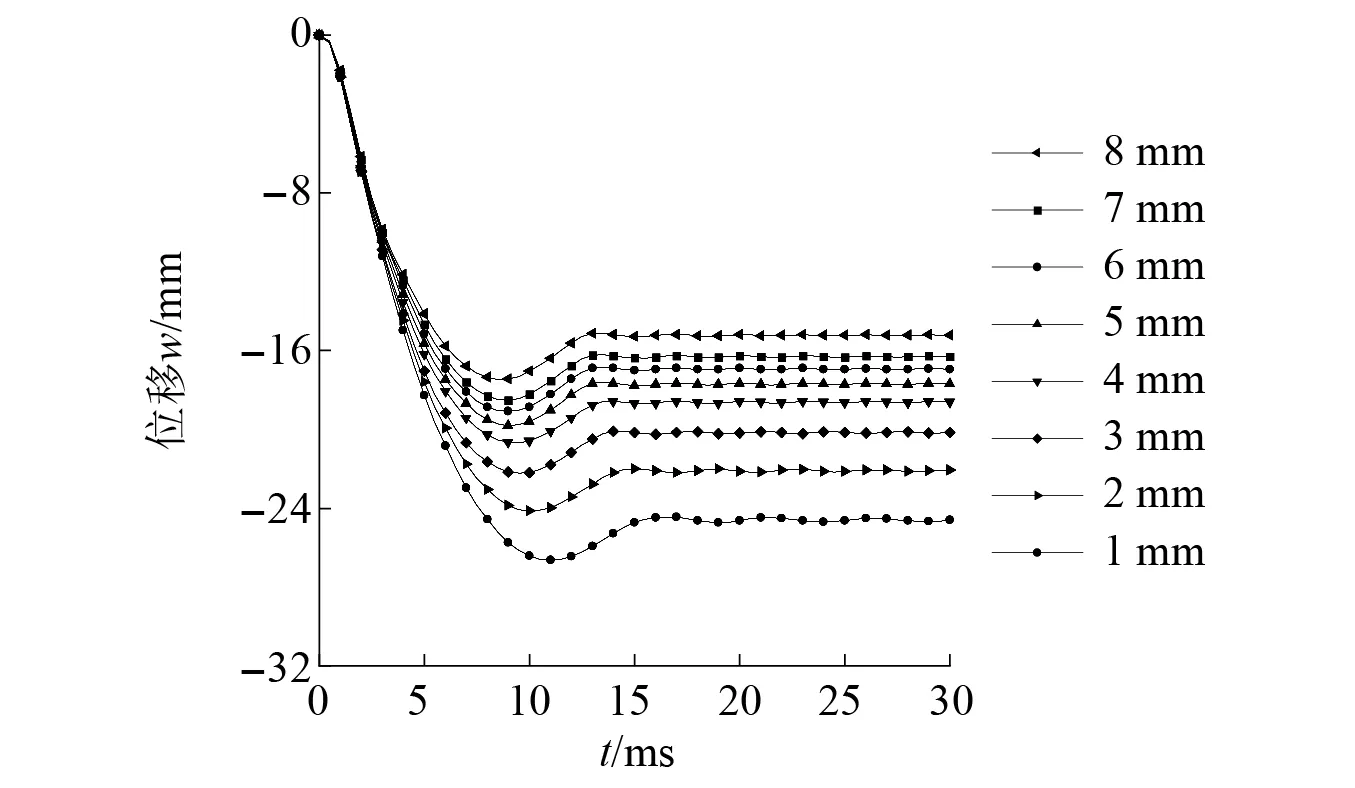
图13 不同钢板厚度下板底中心位移时程曲线

图14 不同钢板厚度下板底最大位移及残余位移
3 Half-SC板动力响应计算方法
3.1 等效单自由度模型
如图15所示,等效单自由度系统由表示结构等效质量m1和冲击物质量m2的质点、表示结构刚度k的弹簧单元和表示结构阻尼c的阻尼单元构成。其运动微分方程为
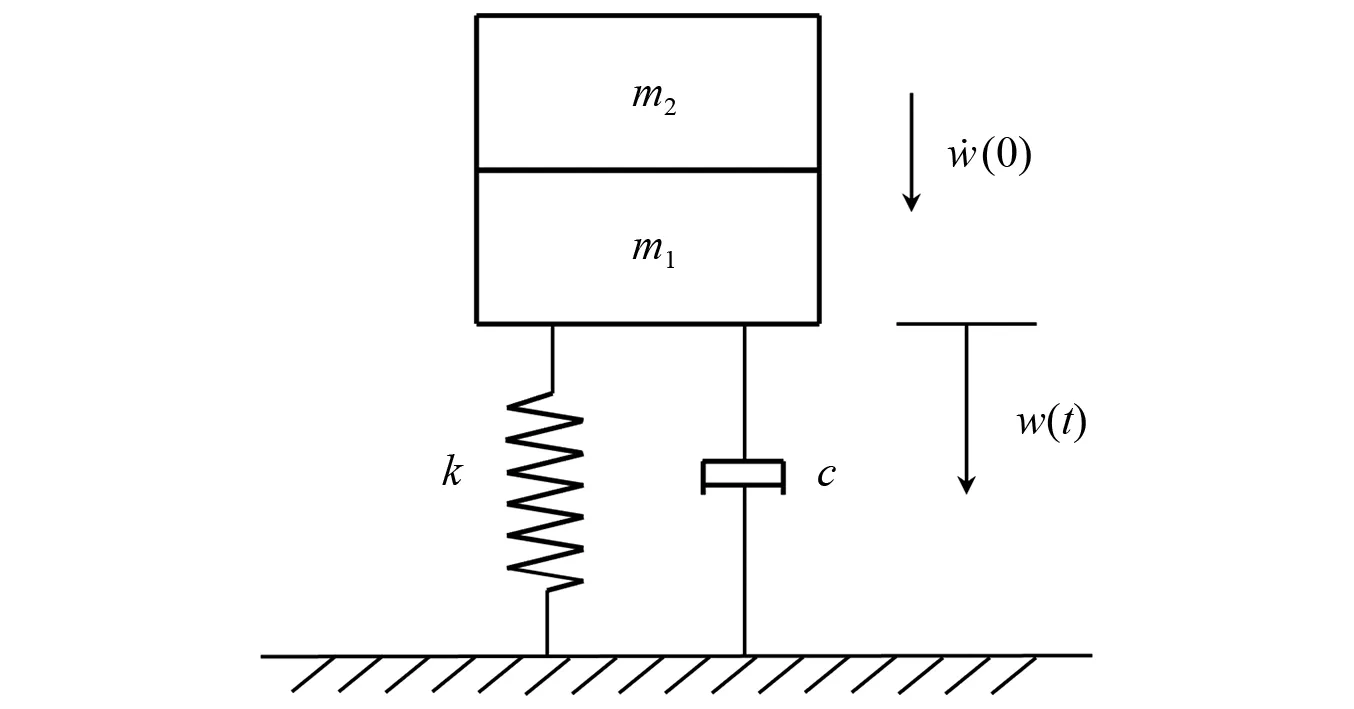
图15 单自由度系统
(2)
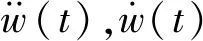
通常情况下,实际结构并不是一个质点,而具有连续分布的质量。对于这样具有无限自由度的结构,需要对其进行简化,将连续分布的质量转化为等效的集中质量。等效后结构与冲击物的质量me为
me=kmm1+m2
(3)
式中:m1为板的质量;m2为冲击物的质量;km为等效质量系数。等效质量系数km随着板的变形不断发生变化[16],km的计算公式为
(4)
式中:形函数φ(x,y)为板在任意时刻的变形,板的中心变形最大,φ(0,0)=1,其他位置φ(x,y)<1;A为板的面积。
根据有限元的结果提取板各点位移,计算得出的km随着板的变形增长变化。本文取弹性阶段km=0.8,塑性阶段km=0.4。另一方面,弹性阶段整块板参与受力,而进入塑性阶段仅冲切开裂锥体运动,板的有效质量减小,因此上述取值是合理的。
由于冲击作用的时间很短,在加载过程中的阻尼通常可以忽略;但在卸载阶段,构件自由振动幅度衰减的很快,在模型中应考虑阻尼的贡献,本文取阻尼比为50%。结构阻尼c计算公式为
(5)
式中,k为板的初始刚度。
弹簧的刚度描述了结构抵抗变形的能力,即结构的刚度。如果结构发生非弹性响应,则其刚度随着变形的发展而发生变化,弹簧的抗力可由抗力函数R[w(t)]表示。3.2节将具体介绍Half-SC板的抗力函数。
本文采用有限差分法求解等效单自由度模型微分方程。其中,微分方程的初始条件为
w(0)=0
(6)
(7)
式中,v0为落锤与结构发生接触的瞬时速度。
3.2 抗力函数
Half-SC板的荷载-位移曲线,如图16所示。由图16可知,在落锤与试件接触的初期,试件H10~H25的荷载表现出较为明显的惯性效应。而在其他阶段,冲击试验试件的加载曲线走势与静力试验试件的加载曲线基本一致。
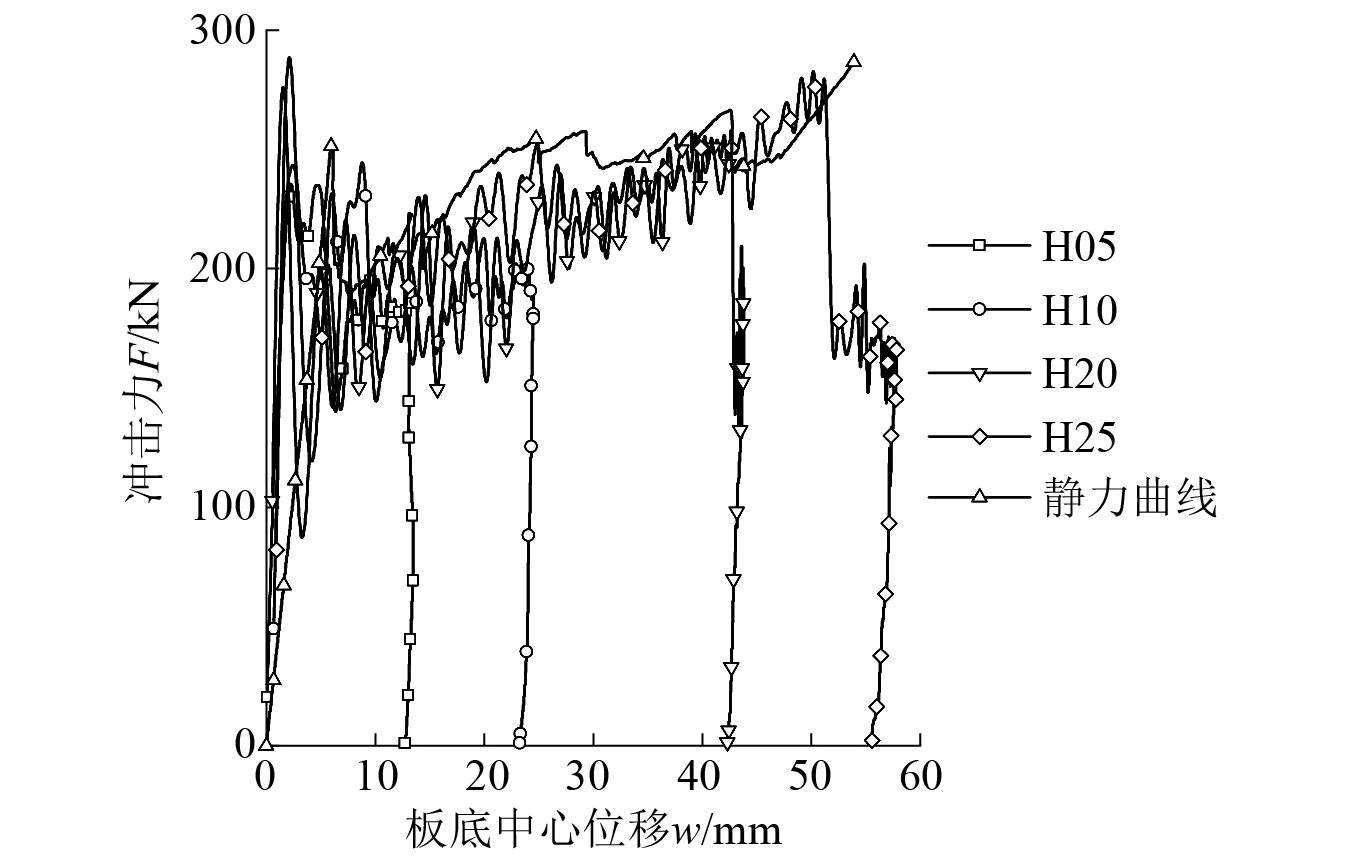
图16 试验试件的荷载-板底中心位移曲线
同时,现有试验中的5片Half-SC板在受冲击后均发生局部冲切破坏,与Half-SC板在静力加载下的破坏模式相同。研究表明,当构件在冲击和静力作用下的破坏模式相同时,可以采用静力作用下的抗力函数进行动力响应分析[17~19]。
根据试验结果,可以提出如图17所示的抗力函数对Half-SC板的非线性力学行为进行描述。图中:OA段为弹性阶段,此时抗力与板底中心位移近似呈线性关系;到达A点后,核心混凝土出现冲切破坏,抗力突然下降;由于钢板、抗剪钢筋和水平钢筋仍能正常发挥作用,BC段抗力再次增加;C点处,试件承载能力达到极限,水平钢筋部分断裂,抗力迅速降低;D点之后,Half-SC板通过抗剪钢筋和未断裂水平钢筋抵抗荷载,从而提供一定的剩余承载力。
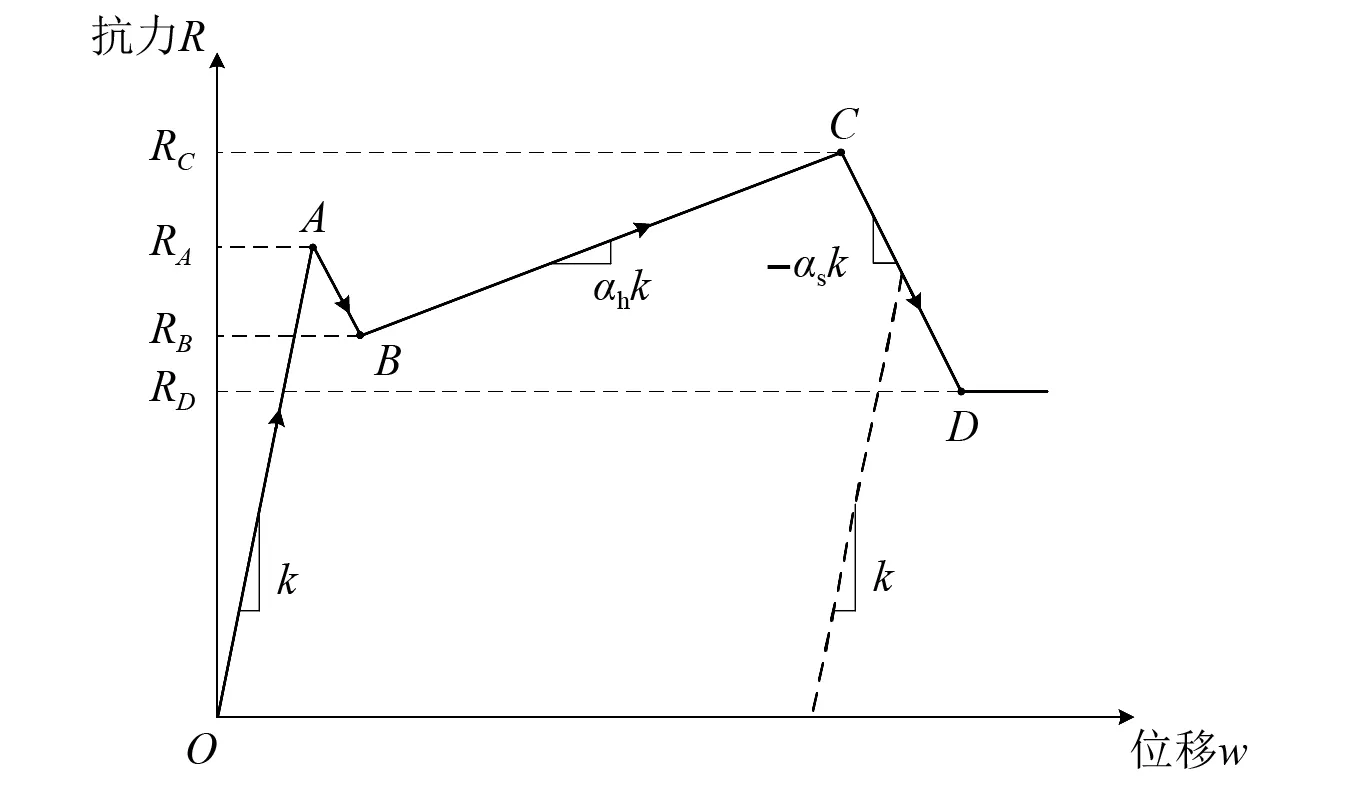
图17 抗力函数模型
3.3 抗力计算
3.3.1 冲切开裂抗力
如图18所示,集中荷载F由抗剪钢筋拉力T、混凝土剪力Vc以及水平钢筋剪力Vs承担。在A点,混凝土即将出现冲切开裂,抗剪钢筋和水平钢筋进入屈服阶段。Half-SC板的冲切开裂抗力RA为
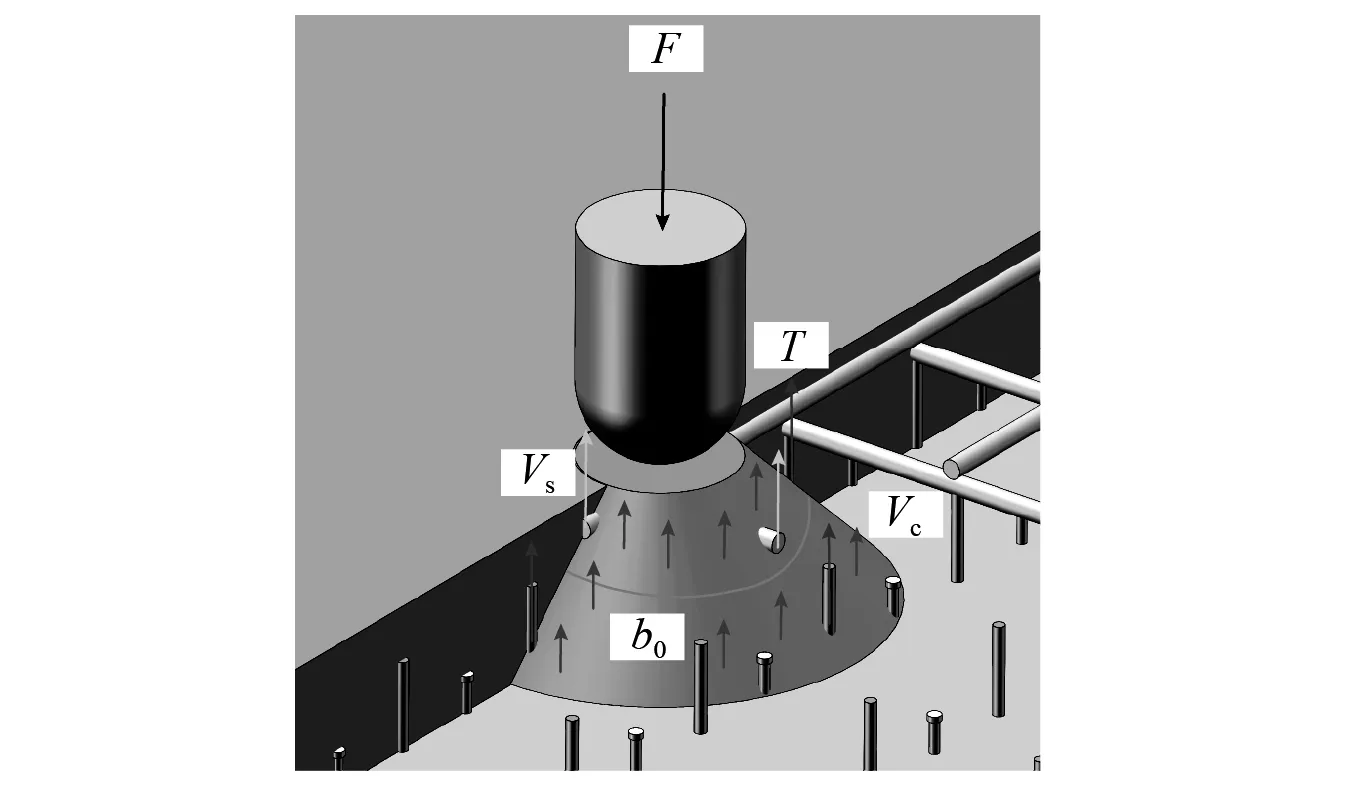
图18 冲切开裂抗力计算模型
RA=nvTy+Vc+Vsy
(8)
式中:nv为穿过混凝土破坏面抗剪钢筋数量;Ty为单根抗剪钢筋的拉力,可采用式(9)计算[20]
(9)
式中:Tty为抗剪钢筋拉伸屈服抗力;Tpy为钢板的剪切屈服抗力;dt为抗剪钢筋直径;σty为抗剪钢筋屈服强度;fpy为钢板屈服强度。
核心混凝土抗剪承载力Vc为
(10)
式中:fc为混凝土轴心抗压强度;tc为混凝土厚度;b0为混凝土冲切锥体在其一半厚度对应的周长。
水平钢筋提供的剪力Vsy为
(11)
式中:ns为穿过混凝土破坏面的水平钢筋数量;ds为钢筋直径;fsy为钢筋屈服强度。
3.3.2 开裂后抗力
混凝土冲切开裂后,部分混凝土退出工作,Half-SC板抗力有所降低,开裂后抗力RB为
RB=nvTy+ηVc+Vsy
(12)
式中,η为混凝土剪力折减系数,根据静力试验结果,本文取η为0.6。
3.3.3 极限抗力
由于混凝土裂缝的不断开展,混凝土完全退出工作。抗剪钢筋和水平钢筋产生较大变形,其应力进入强化段。因此,Half-SC板的极限抗力RC由抗剪钢筋极限拉力Tu和水平钢筋剪力Vsu组成。
RC=nvTu+Vsu
(13)
抗剪钢筋极限拉力按式(14)计算
(14)
由图7可知,在Half-SC板破坏时,水平钢筋产生较大变形,钢筋中出现轴向应力参与抵抗荷载。由于轴力大小和方向未知,为简化计算,按照截面配筋率相同将水平钢筋等效为钢板,并按Guo等[21]提出的Full-SC板计算方法进行估算
(15)
式中:tse为等效钢板的厚度;fsu为水平钢筋的极限强度;Es为钢筋的弹性模量;Ec为混凝土的弹性模量;εsu为钢筋的断裂应变。
3.3.4 破坏后抗力
当Half-SC板发生破坏时,仅部分水平钢筋发生断裂,未断裂水平钢筋仍可继续承担荷载,结合静力试验结果,将水平钢筋贡献削减50%予以考虑。破坏后抗力RD为
RD=nvTu+0.5Vsu
(16)
3.4 刚度计算
在Half-SC板屈服前,板的抗力R与位移w之间呈线性关系
R=kw
(17)
如图19所示,Half-SC板的位移w由整体变形δg和局部鼓起变形δb两部分组成。若将整体变形刚度记为kg,局部变形刚度记为kb,则有
图19 Half-SC板变形分解
(18)
解得
(19)
3.4.1 整体变形刚度
根据板壳理论,在弹性范围内,中心受到集中荷载的四边简支正方形Half-SC板的整体刚度为
(20)
式中,D为Half-SC板的弯曲刚度。
对于组合结构,弯曲刚度可按钢板和混凝土两部分进行叠加计算。对混凝土的抗弯刚度乘以0.7的折减系数以考虑混凝土在A点处产生的部分塑性变形[22-23],即
D=Dp+0.7Dc
(21)
式中,Dp,Dc分别为钢板和混凝土的弯曲刚度。
(22)
(23)
式中:Ep,Ec分别为钢板和混凝土的弹性模量;νp,νc分别为钢板和混凝土的泊松比。
3.4.2 局部鼓起刚度
随着混凝土冲切锥体的形成,荷载传至底部钢板,造成钢板的局部鼓起。由于抗剪钢筋的拉结作用能够在一定程度上抵抗局部鼓起,并将力通过水平钢筋传递至整个构件,本文综合考虑整体刚度和抗剪钢筋的组合效应计算局部鼓起刚度[24]
kb=4πfptp+0.15βkg
(24)
(25)
式中:β为组合作用调整系数;ρp,ρT分别为钢板和抗剪钢筋的含钢率。
3.5 应变率效应
Zhao等[25]对Full-SC板在冲击作用下的应变率效应进行了有限元模拟和理论分析,结果表明仅冲击局部区域的应变率较大,而其他大部分区域的应变率很小。在低速冲击作用下,结构的整体变形分析可以忽略应变率效应,局部接触部分仍需考虑应变率对结构动力响应的影响。
事实上,在冲击过程中,结构各个位置的应变率都不相同;同时,应变率随时间不断发生变化。因此,为计算简便,宜取在空间和时间上具有平均意义的动力放大系数。具体取值参考美国ANSI/AISC N690s1-15规范给出的材料动力放大系数,如表4所示。
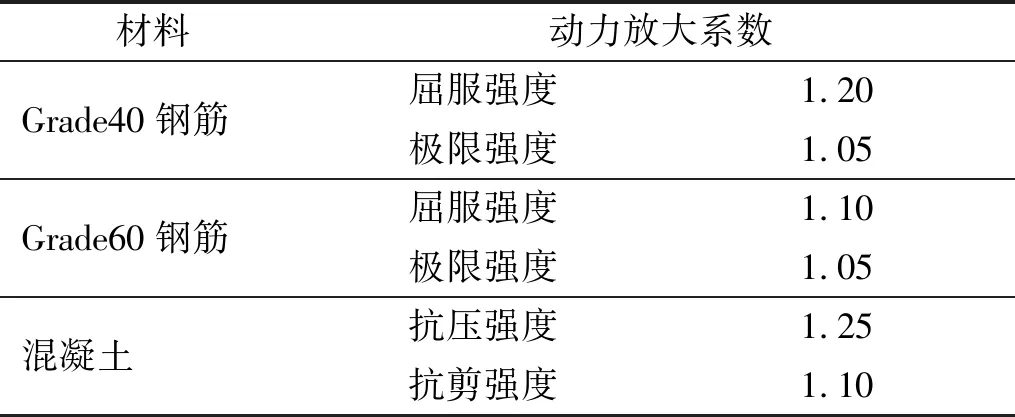
表4 材料动力放大系数
因此本文计算动力响应时将混凝土抗剪承载力Vc放大1.1倍,水平钢筋剪力Vsy以及抗剪钢筋拉力Ty放大1.2倍,水平钢筋剪力Vsu以及抗剪钢筋拉力Tu放大1.05倍。
3.6 计算结果对比
SDOF模型计算得出的Half-SC板底中心位移时程和试验曲线对比, 如图20所示。其中,由于意外原因试件H15的板底中心位移时程缺失。由图20可知,SDOF模型计算结果与试验结果吻合良好。
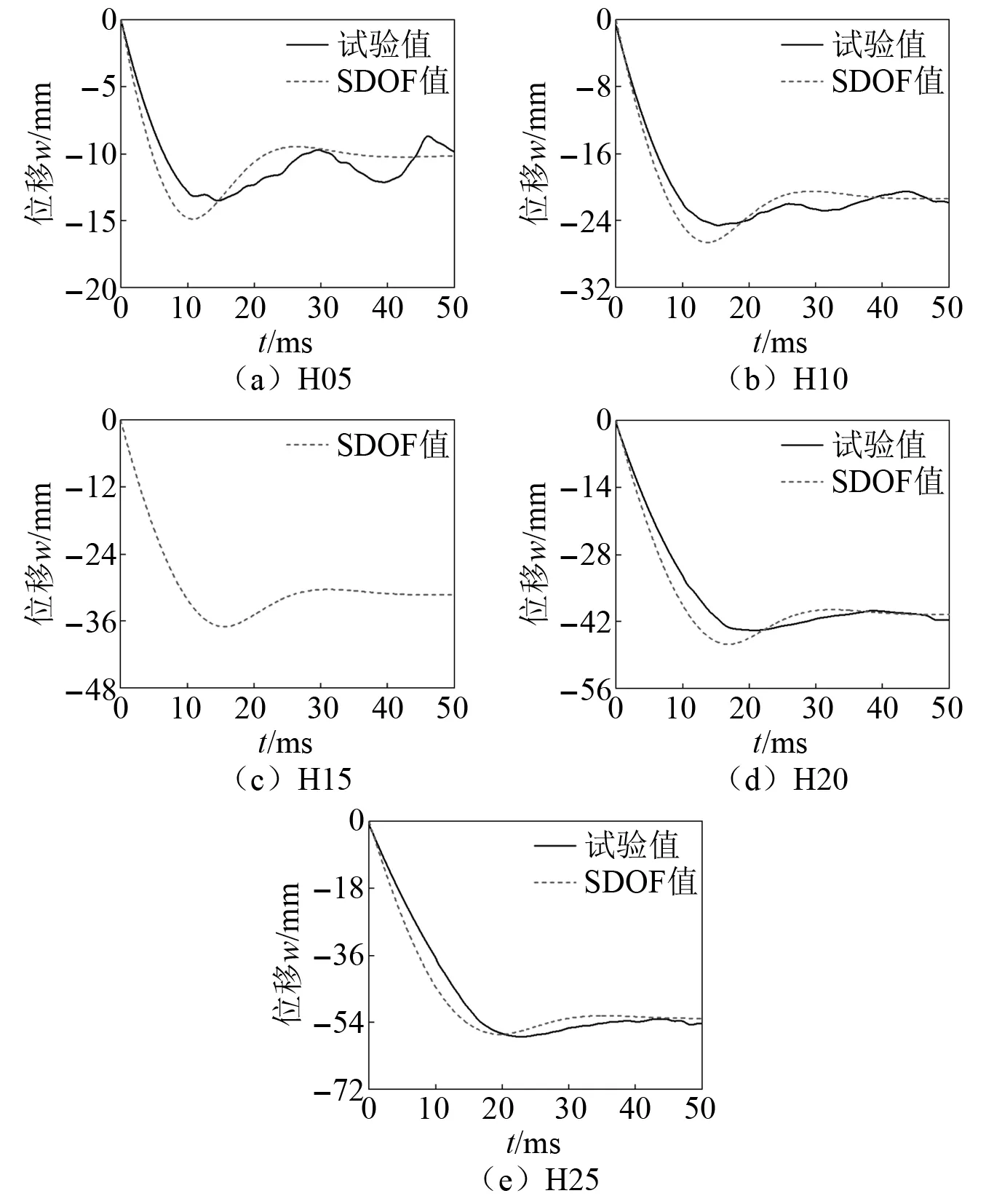
图20 SDOF法与试验曲线时程对比
为进一步验证SDOF模型的准确性,将参数分析得到的结果与SDOF模型的计算结果进行对比,结果如表5所示。表5中,模型编号规则如下:以第一个字母M和数字表示冲击质量;以第二个字母V和数字表示冲击速度;以第三个字母T和数字表示钢板厚度。如M200V5T6,代表冲击质量为200 kg,冲击速度为5 m/s,钢板厚度为6 mm的模型。
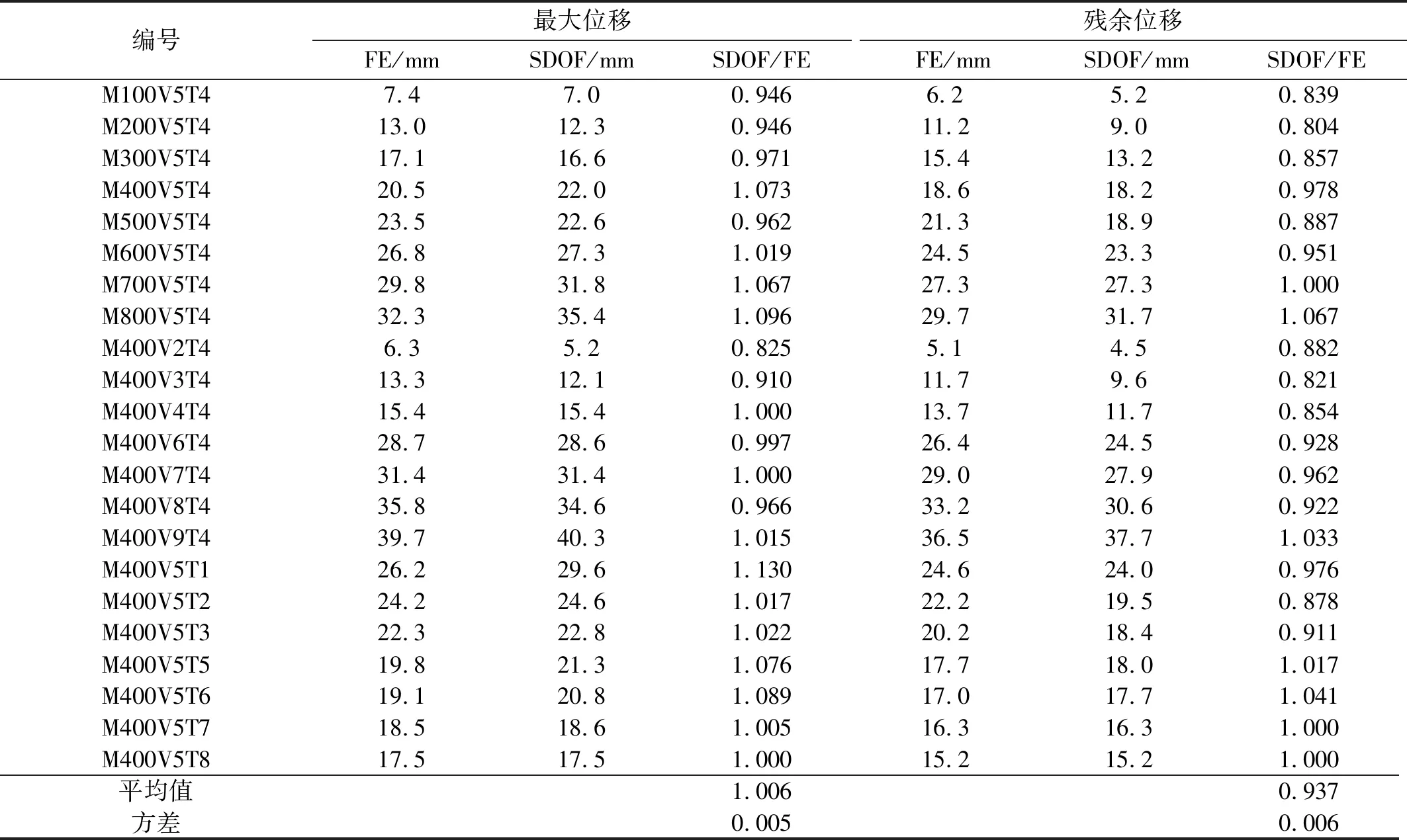
表5 SDOF模型计算结果与有限元分析结果对比
由表5可知:SDOF模型的最大位移计算值与有限元计算值之比的平均值为1.006,方差为0.005;SDOF模型的残余位移计算值与有限元计算值之比的平均值为0.937,方差为0.006。因此,本文提出的SDOF模型可以较准确预测Half-SC板的位移响应。
4 结 论
本文基于LS-DYNA开展了冲击作用下Half-SC板的数值模拟,研究了冲击物质量、冲击速度和钢板厚度对Half-SC板动力响应的影响规律,建立了Half-SC板位移响应时程的等效单自由度模型。得出主要结论如下:
(1) 有限元模型能够很好地模拟Half-SC板的冲切破坏,冲击力时程和位移时程计算结果与现有试验结果符合良好。
(2) Half-SC板在冲击作用下的破坏过程可分为弹性受力阶段,混凝土冲切开裂阶段,水平钢筋断裂阶段。
(3) 冲击速度对Half-SC板位移响应的影响最大,冲击物质量次之,钢板厚度的影响最小。
(4) 推导了Half-SC板的抗力和刚度计算式,提出了等效单自由度模型全部参数的计算方法,位移时程的理论计算结果与现有试验结果和有限元参数分析结果符合良好。
