轧件激励诱发CSP轧机振动问题研究

张义方, 何 成, 崔 立, 王才峄

(上海第二工业大学 工学部 机械电子工程系,上海 201209)

随着复杂机电装备向高速、重载和超精度控制方向发展,工作对象负载及工况环境对系统动力学特性影响问题需要给予足够重视,如:轨道激励对高速机车行驶动力学特性影响问题[1]、路面激励对汽车系统动力学特性影响问题[2-3]、隧道硬岩掘进机(tunnel boring machine,TBM)的破岩动态激励问题等[4]。在冶金轧钢生产中同样需要面对在极限工况下的轧制失稳问题[5]。紧凑式带钢生产(compact strip production,CSP)线连铸连轧生产具有流程紧凑、投资少、能耗低等优势是冶金界的一项前沿技术,已在国内多家钢厂得到普及应用,但其在轧制薄带高强钢时出现的强烈振动行为仍然是行业的一大难题[6]。

轧机作为一个大型复杂机电一体化装备,其振动形式多样,机理较为复杂,国内外学者一直在进行轧机振动机理和振动控制方面的研究工作,取得了一系列有价值的研究成果[7-15]。轧机振动机理研究一般从轧机机座系统、工作界面、主传动系统建模等研究其动力学行为特征[16-19]。CSP工艺与传统板材生产工艺要求有所不同,因此CSP轧机在极限工况下,有时会表现出与常规轧机差异化的动力学特征。在CSP轧机振动研究领域,文献[20]重点对CSP轧机中工作辊的水平振动和主传动系统的扭转振动进行分析研究,得出辊系水平振动是由扭转振动引起的强迫振动的结论。文献[21]针对某厂CSP F3轧机振动问题研究了主传动扭振与辊系垂振的耦合关系,确定传动系统与辊系二阶水平固有频率接近时系统发生强烈振动的频率特征。这些研究极大丰富了CSP轧机振动的研究内容,为探讨CSP轧机振动机理提供了非常有意义的参考价值。然而其中一个未被引起足够重视的影响因素就是轧件本身特性对轧机系统动力学行为影响问题。虽然有关文献在研究中考虑过轧件影响因素,但由于引起轧机振动原因众多,其重要性在众多的研究内容中未被充分凸显,实际情况是在轧制过程中传动和压下系统都与轧件相关联,轧件是影响轧机系统动力学特性的重要因素,而CSP轧机因其轧件宏观尺寸及微观组织特性与其他型式轧机带材存在区别[22],因而研究CSP轧制工况下的轧件对轧机系统特性影响问题显得异常重要。

本文正是基于以上背景和目的,结合某钢企CSP轧机振动问题,利用测试试验的方法在工业现场证实轧机存在轧件激励的振动特征,结合理论研究及仿真求解,分析此类振动机理,并提出抑振措施,研究为提高轧机系统稳定性、改善轧材质量和企业降本增效提供参考。

1 工业现场试验研究

某厂CSP热连轧机共包括F1～F7七台精轧机,现场图片如图1所示,轧件经过F1～F7轧机依次精轧变薄后经卷曲机卷绕成成品钢卷。其在轧制SPHC钢种(轧制1220-65-1.6 mm规格)时F2轧机出现强烈振动,其他单元轧机振动不明显,现场观测F2轧机出入口轧材表面有可见条纹。

图1 CSP轧机现场现象

为了解其振动特性,通过现场安装在线监测系统对其振动进行在线测试(如图2(a)所示),在轧辊轴承座安装加速度传感器(如图2(b)所示)以及在传动端接轴安装应变片(如图2(c)所示)获取轧机辊系及电机主传动系统振动波形及频谱如图3和图4所示。

图2 轧机系统现场测试

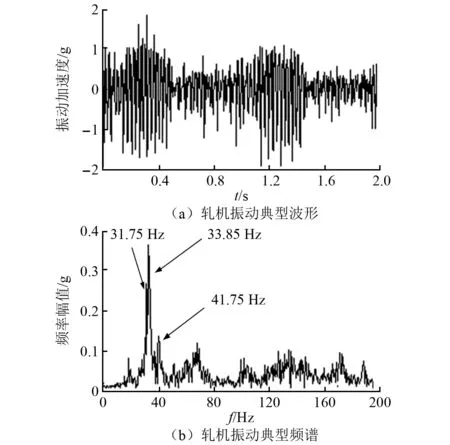
图3 轧机垂振波形及频谱

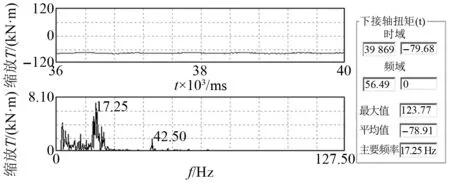
图4 主传动系统典型振动波形及频谱

图3为轧机垂振时域波形和频谱,从图3中可以看出垂直方向振动呈现典型的拍振特征,振动幅值最大值接近2.0g,振动主频为33.85 Hz。图4为监测获得的主传动扭振主频为17.25 Hz,振动频谱中含有42.5 Hz频率成分。此时轧机振动特征表现为主传动以低频扭振为主,而垂直系统以高频垂振为主的振动形态,主传动与轧机辊系都有42 Hz左右的振动分量存在,但轧机垂直系统42 Hz振动未能被激发而表现为33.85 Hz频率的拍振,而传动系统33.85 Hz频率的振动却未被激发。鉴于此并结合现场观察F2轧机入口轧件表面周期波动现象,推测此时F2轧机垂直系统振动或与一定工况下的轧件激励存在关联,欲利用工业现场咬钢冲击试验以及动压靠试验进一步帮助分析判断。

1.1 咬钢冲击试验

咬钢冲击试验可以监测获得轧机系统在突加冲击载荷作用下的振荡衰减响应。试验钢种为SPHC,规格为1220-65-2.2 mm,轧制速度2 m/s,利用在线监测系统获得轧辊在冲击载荷作用下的振动曲线及频谱,如图5所示。

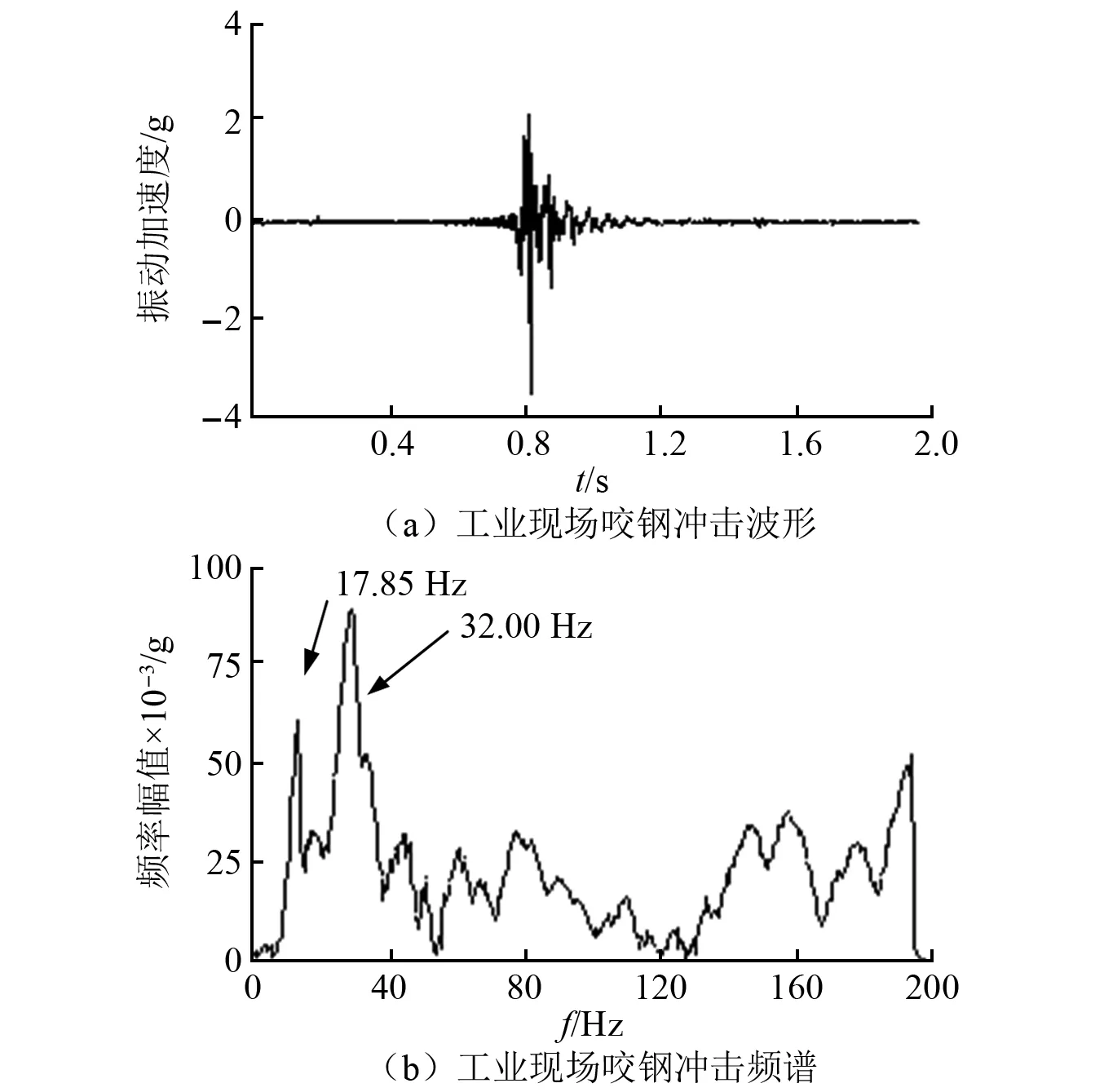
图5 工业现场咬钢冲击试验波形及频谱

从图5中可以看出,轧机系统在阶跃冲击作用下瞬间表现为自由衰减振动,频谱分析显示其衰减振荡主频为32 Hz,由振动理论知识可知其可以初步反应轧机的固有频率特性[23](后面通过有限元计算进行数值求解)。

1.2 工业现场动压靠试验

现场动压靠试验是轧机在正常轧制工艺参数状态运行但无轧件咬入时进行设备加载模拟轧制试验,通过该试验可以了解轧机设备本体(无轧件影响工况下)的行为特性,图6为轧机动压靠下监测获得的轧机振动时频谱。

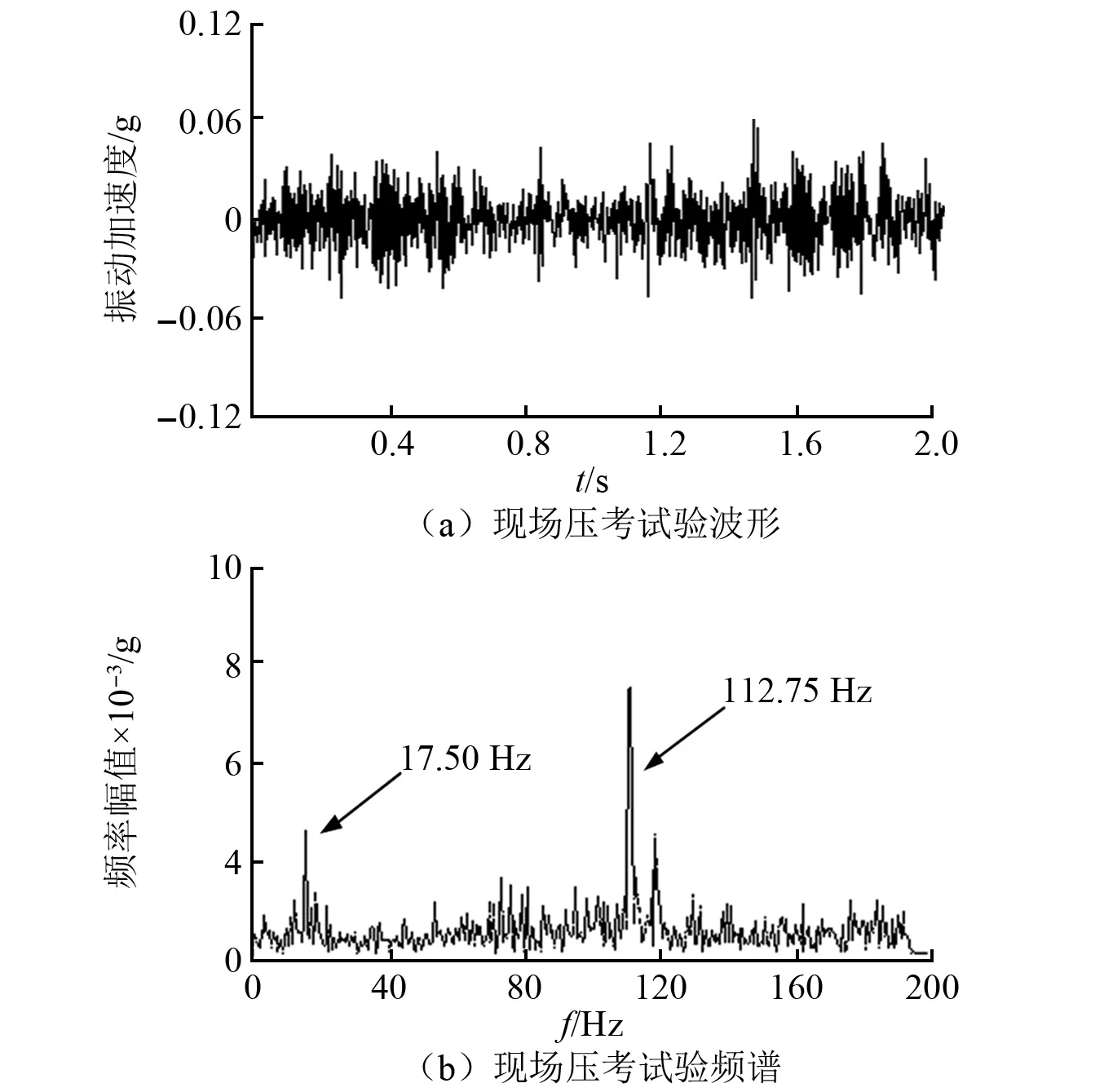
图6 轧机压靠试验时频图

从图6中可以看出,轧机本体(无轧件工况下)振动幅值很小,最大值接近0.06g,频率较为分散,主要振动频率为112.75 Hz的高频,此频率远高于现场测试轧机振动频率,轧机无明显强振特征。

鉴于以上分析,综合判断F2轧机振动与咬入轧件激励紧密相关。由轧制理论知识可知,轧件进入轧机轧制时发生塑形变形,在轧辊上有轧制力来对抗轧件的变形抗力,下面通过轧制理论数学模型研究轧件厚度波动变化对轧制力的影响机理。

2 轧件厚度波动影响轧制力波动机理

轧件厚度波动不均时轧制过程示意图,如图7所示。

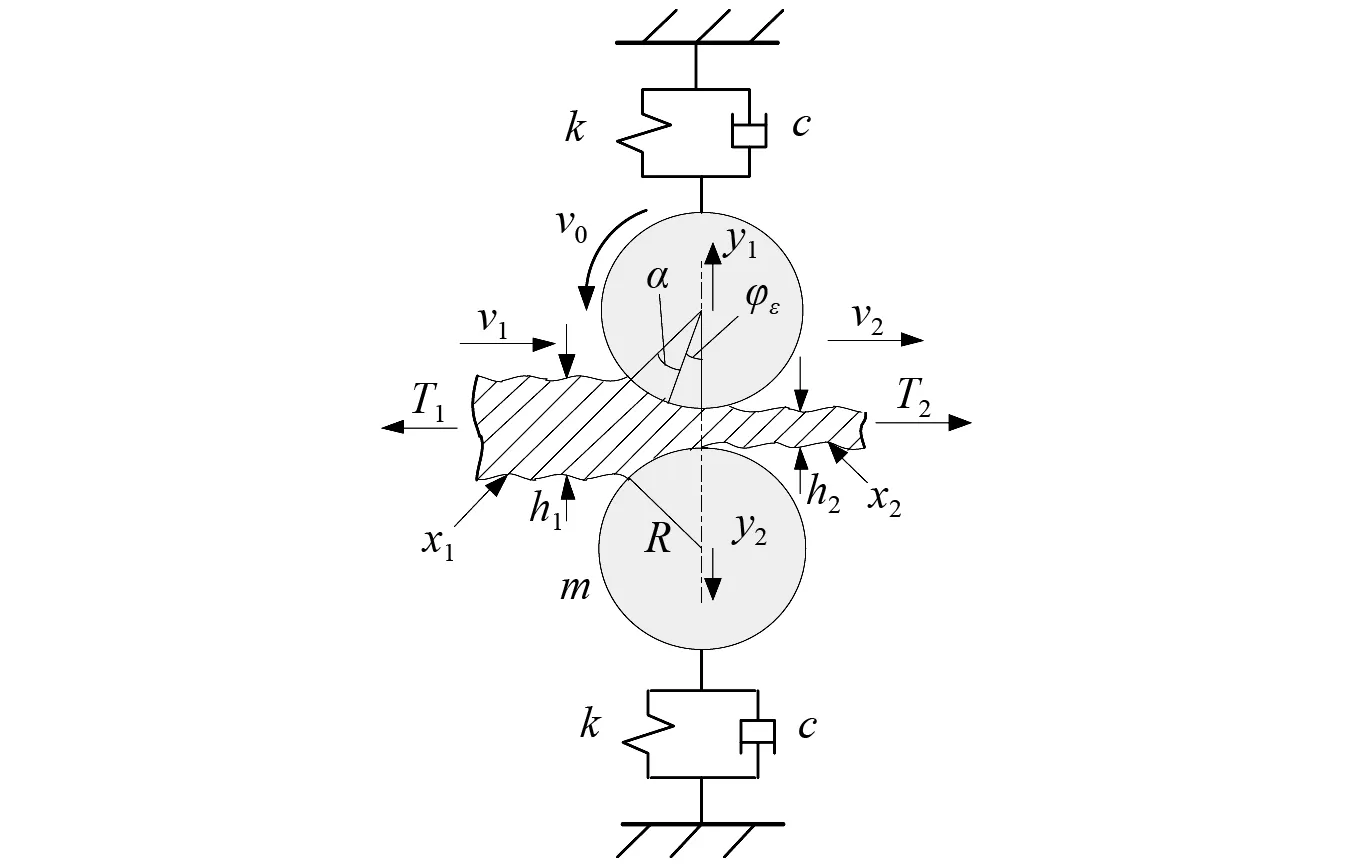
图7 轧制过程示意图

图7中:α为咬入角;φε为轧辊与带钢接触处某与辊系垂直方向的夹角;v0为轧辊表面线速度;v1,v2分别为轧件入口与出口速度;T2,T1分别为前、后张力;h1,h2分别为带钢入口和出口厚度;R为轧辊半径;k,c分别为轧辊与牌坊机架间的刚度与阻尼;m为轧辊质量(设上、下轧辊结构尺寸对称分布);y1,y2分别为上、下轧辊的振动位移。

当理想工况轧件无厚度波动不均时,由轧制理论可知,轧制力公式表示为[24]

P=BlcQpKtK

(1)

式中:B为钢坯宽度;lc为接触弧长;Kt为张力影响系数;Qp为应力状态系数,其表达式为

Qp=0.804 9-0.339 3ε+

(2)

式中,ε为压下率。

(3)

(4)

(5)

式(1)中,K=1.15σ,σ为金属塑性变形阻力,

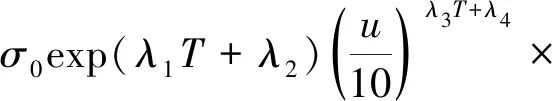
(6)

式中:T为变形温度;e为变形程度;u为平均变形速度;σ0为一定标准工况下的变形阻力;λ1～λ6为回归系数。连轧机秒流量相等原理可得

h1v1=h2v2

(7)

而v2=v0(1+Sh),v1=v0cosα(1-SH),其中,Sh和SH分别为前滑、后滑系数,从轧制力式(1)可以看出其值受多个参数影响:轧件尺寸、轧制速度、轧件变形阻力、硬度以及可能的内部成分组织等。限于篇幅,依据工业现场实际现象,这里仅研究轧件厚度波动对轧机轧制力影响特性。

设轧件表面入口厚度波动值为x1,无厚度波动值为h10,出口带钢厚度波动为x2,无厚度波动值为h20。则在此类工况下,上述式(3)、式(4)及式(5)依次变为式(8)、式(9)及式(10)

(8)

(9)

(10)

(11)

而轧件在整个变形区的平均变形速度为其在整个接触弧长上变形速度的平均值

(12)

又由连轧机秒流量相等原理可得

(h10+x1)v1=(h20+x2)v2

(13)

v2=v0(1+Sh)

(14)

v1=v0cosα(1-SH)

(15)

式中,Sh和SH为轧机的前、后滑值。

(16)

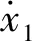
(17)

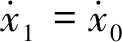
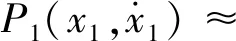
(18)

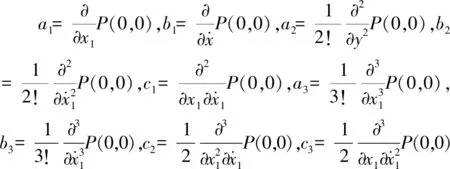
(19)

其中,

a1cos(ωt+φ)-b1Asin(ωt+φ)+a2A2cos(ωt+φ)2+

b2A2sin(ωt+φ)2-c1A2cos(ωt+φ)sin(ωt+φ)+

a3A3cos(ωt+φ)3-b3A3sin(ωt+φ)3-

c2A3cos(ωt+φ)2sin(ωt+φ)+

c3A3cos(ωt+φ)sin(ωt+φ)2+…=

a1cos(ωt+φ)-b1Asin(ωt+φ)+

(20)

因此,式(19)可简写成轧制力波动关于频率的函数形式

可见在轧机轧制厚度波动不均的轧材时,其轧制力会产生与轧件厚度不均引起的周期及倍频成分。也就是说轧制力中除了基波频率外还含有2次、3次等倍频谐波分量。

将轧制力波动作为轧机辊系的外源激励之一,由图7所示列写轧机垂向振动动力学方程的一般形式

(21)

上、下两式相加,令y=y1+y2,得到

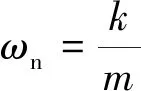
3 轧制过程有限元计算仿真研究

金属轧制过程是一类复杂的非线性弹塑性变形过程,本题研究轧件厚度波动对轧机特性影响问题,对于这类难于用精确数学模型进行求解的非线性动力学问题,利用有限元法进行仿真求解可以获得较为贴近实际的求解结果。为分析轧件在厚度波动影响下的轧制力特性,这里利用ANSYS/ LS-DYNA软件做进一步研究,首先利用ANSYS有限元对轧机垂直系统固有频率进行计算以帮助分析轧机特性。

3.1 轧机固有特性计算

为了解轧机机座系统固有特性,前面通过试验方法初步获得轧机垂向振动频率31.5 Hz(见图5),这里利用有限元数值计算的方法获得其固有特性,整个系统的材料为合金钢,材料密度为7 800 kg/m3,弹性模量为210 GPa,泊松比为0.3,依据现场提供的设备结构几何尺寸及参数建立ANSYS有限元模型(如图8所示),计算获得轧机垂向1～4阶模态频率如表1所示。

表1 轧机垂振固有模态频率

图8 轧机有限元仿真计算

其一阶模态频率为30.3 Hz(考虑有限元计算会与实际存在一定误差)与工业现场振动测试得到的轧机振动频率31.75 Hz及31.5 Hz接近。依据现场咬钢阶跃冲击响应试验和有限元数值计算可推断轧机垂向一阶固有频率在31 Hz左右,综合现场压靠(无轧件工况时)试验现象特征可进一步推断轧机振动(拍振)由与其垂向一阶固有频率相近的频率激发引起。

3.2 轧制动态过程仿真计算

利用ANSYS/LS-DYNA对轧材轧制过程进行仿真计算,依据现场轧机参数及工艺PDA数据设定:轧件宽度为1 220 mm;轧件入口厚度为32 mm;轧件出口厚度为15 mm;轧件前张力为0.5 MPa;轧件后张力为0.3 MPa;轧件弹性模量为1.17×1011Pa;轧件泊松比为0.362;厚度波动峰值为0.3 mm;轧件周期波长为118 mm;动、静摩擦因数分别为0.2,0.3;轧制速度为2 m/s。首先建立轧件模型(如图9所示)以及轧制过程模型(如图10所示,这里因结构对称,不影响研究目的情况下,为简化计算方便采用1/4结构仿真模型)。

图9 轧件模型

图10 轧制过程模型

计算获得轧件的等效应力、应变分布,分别如图11、图12所示。

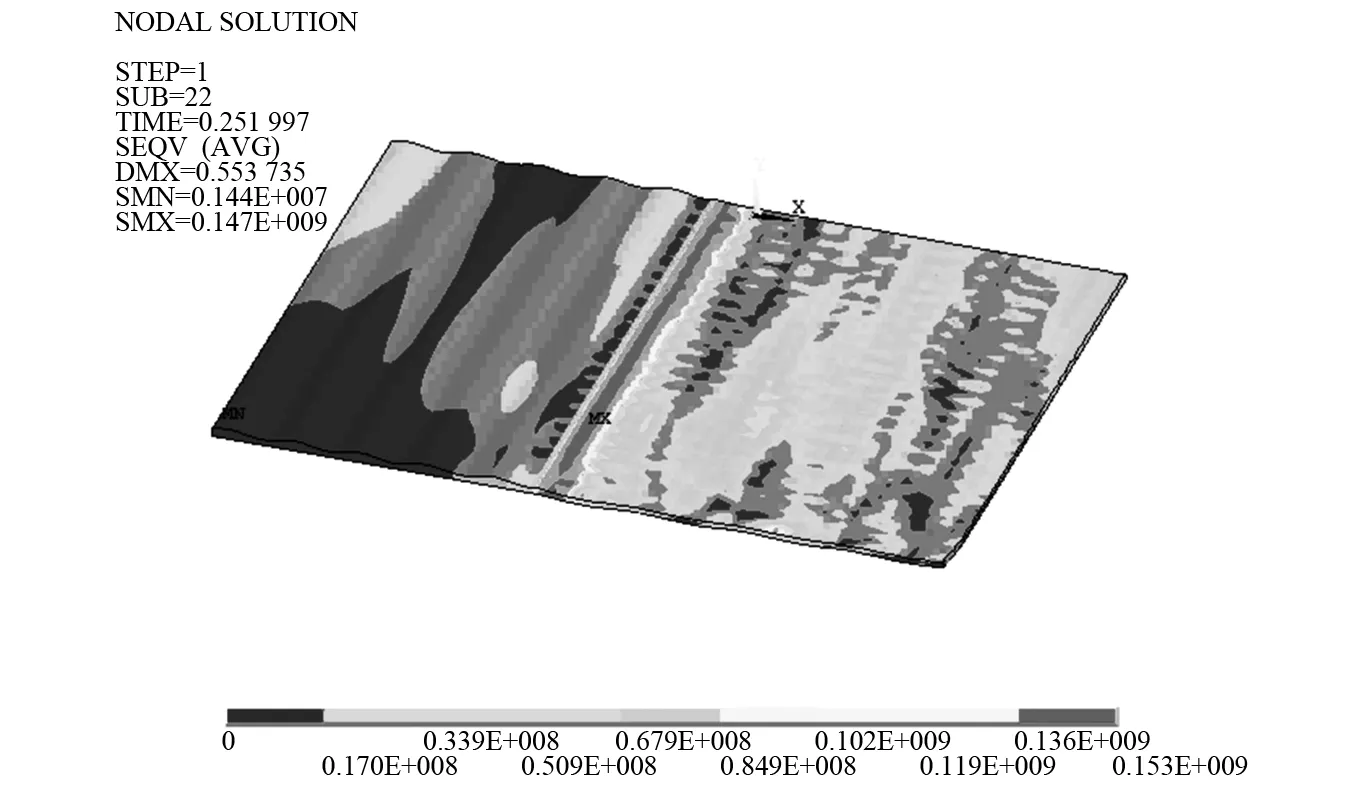
图11 轧件等效应力分布

图12 轧件等效应变分布

由图11和12看以看出,轧机在厚度周期波动工况下,轧件的应力应变分布存在周期性波动变化现象,同时有限元计算获得输出轧制力随时间变化曲线及频谱,如图13所示,从图13可以看出,当轧机入口带材厚度发生波动时轧制力会出现周期性波动现象,且轧制力波动频率含有波动周期频率(16.7 Hz)及其倍频(33.4 Hz),这与上一单元通过建立轧件厚度波动影响的轧制力数学模型分析结论相一致。

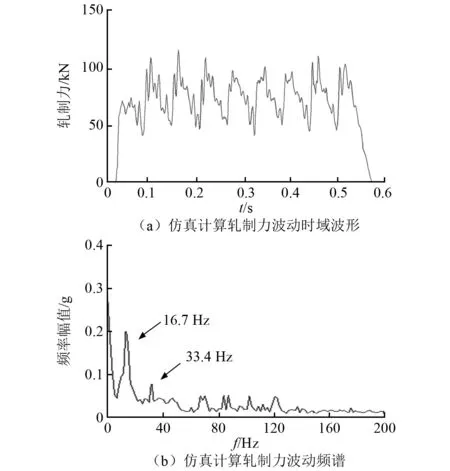
图13 轧件厚度波动时轧制力变化时域频谱

为研究轧制速度对轧制力波动影响特性,依据不同规格工艺速度区间范围,在入口轧件厚度及波动幅值不变情况下,仅改变轧制速度,分别在轧制速度为:0.8 m/s,1.2 m/s,1.6 m/s及2.4 m/s进行ANSYS/ LS-DYNA有限元仿真计算,获得各轧制力波动幅值与轧制速度关联曲线如图14所示。

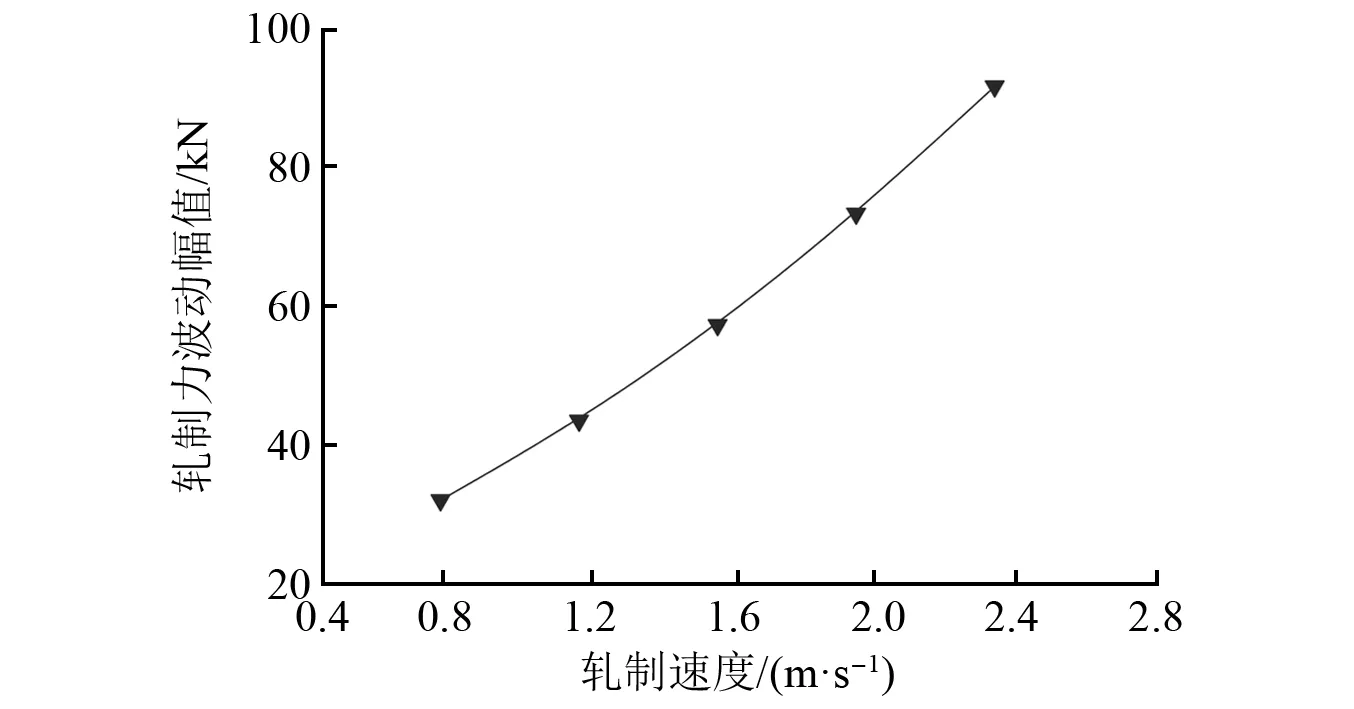
图14 轧制力波动幅值随轧制速度变化

由图14可以看出,随着轧制速度增加,在入口轧件厚度波动幅值保持不变工况下,轧制力波动幅值逐渐增大。反之,当存在轧件厚度波动时,轧制速度越小,轧制力波动越小,越有利于轧制稳定。

4 轧件诱发轧机失稳抑振研究

4.1 抑振依据及方法

由连轧上、下游轧机秒流量方程式(13)(h10+x1)v1=(h20+x2)v2可知,轧制速度变量与厚度变量存在耦合关系。当F2轧机入口轧件厚度发生变化时其轧制速度也会发生改变,因为厚度波动参数x1值较小,对速度影响有限,当入口带钢厚度波动(x1)发生时,入口带钢厚度(h10)增加,轧制速度(v1)相应减小,F2轧机运行在低速区间,获得较好的轧制稳定性。另:入口带钢厚度改变,轧制速度发生改变,随之轧件对轧机的激励频率(含2次、3次等倍频谐波频率)也会发生改变。

因此改变入口带钢厚度可以达到改变轧件激励引起的轧制力波动幅值和波动频率的双重目的。由于连轧机上、下游轧机相关联,欲改变F2轧机入口带钢厚度,需要通过调整轧机上、下游压下分配来完成。

4.2 不同“上、下游压下分配”试验

CSP轧机轧制SPHC钢种(1220-65-1.6 mm规格)时原轧制工艺压下分配如表2所示,其振动幅值及频率见第1章图3。

表2 CSP轧机压下分配(调整前)

现依据上述分析抑振策略,改为新的压下分配如表3所示。

表3 CSP轧机压下分配(调整后)

工艺优化实施后获得轧机振动时频图,如图15所示。从图15中时域波形看出,轧机振动幅值大幅降低,无明显拍振波形,幅值降低90%以上,频谱图显示振动频率分散,未见明显主频振动特征,抑振措施取得较好效果。

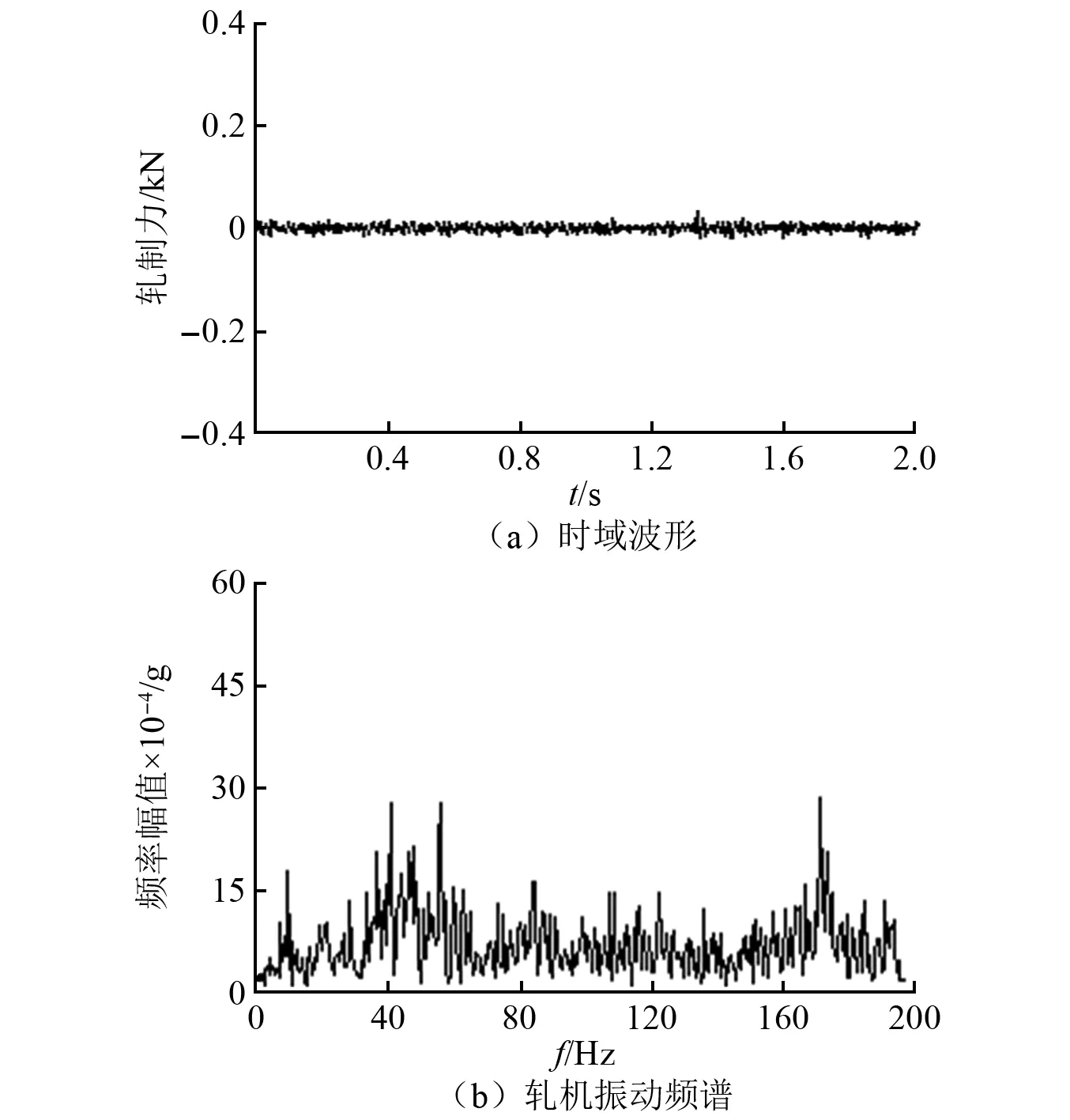
图15 措施后轧机振动时频图

5 结 论

通过工业现场试验、数学建模机理研究及仿真计算得出以下结论:

(1)在工业现场实施轧机振动试验,结果显示CSP轧机在轧制SPHC轧材时F2轧机出现强烈振动,振动主频为33.85 Hz,阶跃冲击响应频率为32 Hz,无轧件工况下振动频率分散未见主要特征。工业现场实证研究表明轧件对轧机动力学特性有重要影响。

(2)利用轧制过程理论模型,分析轧件厚度波动对轧制压下率、接触弧长、轧制速度等影响关系,最终获得轧件厚度波动影响轧制力波动机理模型,数学解析式显示为轧机厚度波动可以激发轧制力产生高频谐波。

(3)针对轧制非线性动态过程理论数学模型求解难的问题,本题使用ANSYS/ LS-DYNA建模求解轧件厚度波动影响问题。结果表明,入口带钢厚度波动在轧制过程中使得轧制力发生波动,且随着轧制速度增加,轧制力波动幅值会增加,波动频率为基频和二倍频。动力学方程分析得出含基频及二倍频轧制力可以激发轧机产生33 Hz左右的拍振。

(4)利用轧件速度与厚度参数耦合特性,合理优化连轧上、下游轧机压下分配,改变上、下游轧机入口、出口厚度,从而改变因入口轧件厚度波动对轧机系统振动特性影响,避免轧件因厚度波动激起轧制力波动诱发轧机失稳的路径,实施后起到较好抑振效果。