Π型叠合梁斜拉桥建造全周期静风失稳模式及机理研究

薛晓锋, 吕盛昌, 曹体锁, 高广中

(长安大学 公路学院,西安 710064)

大跨度桥梁的风致稳定性分析通常包括风致静力失稳和风致动力失稳两个方面。Hirai等[1]于1967年在悬索桥全桥气弹模型风洞试验中首次发现了风致静力扭转发散现象,Xiang等[2]于1997年在汕头海湾二桥风洞试验中出现了弯扭耦合风致静力弯扭耦合现象,同时文献[3]发现一座1 500 m的大跨度斜拉桥中存在有静风失稳与颤振相互竞争问题。程进等[4-5]采用了内外双重迭代方法确定了静风稳定性分析基本方法。目前,许多学者对于不同跨径及主梁截面下对称结构成桥阶段静风稳定性能[6-12]、失稳模式[13-14]、发展路径[15]、失稳机理[16-19]和应对措施[20-23]都进行了深入研究,并有了一定的成果和文献。但目前研究主要针对于成桥运营阶段,而对非对称结构不同施工阶段的静风稳定性发展变化规律的研究非常少。

Π型钢混叠合梁由于自质量轻、施工吊装方便、跨越能力强,在斜拉桥中得到了广泛应用。但是其抗扭刚度小,对风致作用非常敏感,在风荷载作用下易发生失稳现象[24]。施工阶段由于结构尚未形成最终的约束体系,结构刚度尤其是扭转刚度明显不足,同时桥梁施工、运营不同阶段结构气动外形也有变化,会使静风稳定性大大降低,增加扭转发散概率[25]。因此研究低扭转刚度非对称结构施工全过程的静风响应变化特征具有重要的价值和工程意义。

本文以一座主跨跨径480 m的Π型钢混叠合梁非对称斜拉桥为研究对象,通过风洞试验和数值计算分析,展开对多个典型施工阶段和成桥静风失稳形态和失稳机理的分析,研究低抗扭刚度斜拉桥建造全周期静风发散特征和失稳机理。

1 斜拉桥非线性静风稳定理论和数值实现方法

1.1 非线性静风稳定理论

斜拉桥静风稳定理论的力学计算特点是要充分的考虑到结构变位的几何非线性和静风荷载的非线性,材料的非线性由于钢结构在失稳之前难以进入塑性阶段而表现不明显,因而核心的非线性问题是静风荷载非线性和桥梁结构位移非线性。鉴于静风荷载可看作是有效风攻角的函数,静风荷载的非线性通常是通过对有效风攻角的循环迭代实现[26]。将静风荷载对桥梁结构的影响简化为阻力、升力、升力矩三者的共同作用,静风荷载的表达式为

(1)

式中:ρ为空气密度,一般取1.225 kg/m3,本研究取1.25 kg/m3;V为来流风场的风速;有效风攻角α0是结构扭转角与来流风场风攻角之和;CD(α0),CL(α0),CM(α0)分别为与有效风攻角α0有关的阻力系数、升力系数、升力矩系数;FD(α0),FL(α0),FM(α0)分别为结构的阻力、升力、升力矩。

大跨度桥梁考虑结构几何非线性和静风荷载非线性的静力分析可以归结为求解下面的非线性平衡方程

[K(δ)]{δ}={F(α,v)}

(2)

式中:[K(δ)]为桥梁结构的总切线刚度矩阵;{F(α,ν)}为在风速ν和风攻角α下的风载等效节点力向量。

采用UL列式求解,相应非线性增量的平衡方程组为

{[K0]+[Kσj-1(δj-1)]}{Δδj}= {Fj(αj,vi)}-{Fj-1(αj-1,vi)}

(3)

式中:[K0]为大跨度桥梁的线弹性刚度矩阵;[Kσj-1(δj-1)]是迭代至j-1步时的单元几何刚度矩阵;{Δδj}是迭代至j步时的位移增量向量;{Fj(αj,vi)}为第i级风荷载第j步有效风攻角αj下的风荷载等效节点力向量;{Fj-1(αj-1,vi)}为第i级风荷载作用下第j步有效风攻角αj-1下的风荷载的等效节点力向量。

1.2 非线性静风稳定数值计算方法

由于桥梁结构刚度和静风荷载的大小都是结构变形的函数,因此为了求解静风问题的非线性方程,本文采用内、外增量双重迭代的方法。基于编程软件,内层增量迭代完成求解结构变形的非线性问题,外层增量迭代通过控制一定的风速增长步长,获取结构在特定风速下的平衡位置。

计算时首先求解自质量作用下的结构变位,假设初始风速为10 m/s,风速的增加步长为10 m/s,启用应力刚化,通过Newton-Rapson方法进行非线性求解求得桥梁结构在该风速下的位移。若结果收敛,则按照规定增加风速增量;若结果不收敛,则调整更新后的风荷载继续进行Newton-Rapson方法求解直至规定的迭代次数。

2 工程背景

2.1 工程特征及模型

本文研究对象桥梁全长880 m,是一座双塔双索面叠合梁斜拉桥。图1为该斜拉桥的主梁横断面示意图,该主梁采用“π”型断面,梁高3.6 m,宽度为32.5 m,主梁两侧采用“倒L”形导流板,以改善桥梁的抗风性能,栏杆高度为1.6 m。主梁为抗扭刚度较低的“π”形叠合梁断面。桥塔采用钢筋混凝土空心薄壁结构,由于受到两岸地形限制,左侧桥塔与右侧桥塔高度相差7.44 m,桥面采用单向纵坡,因此桥梁为不完全对称结构。

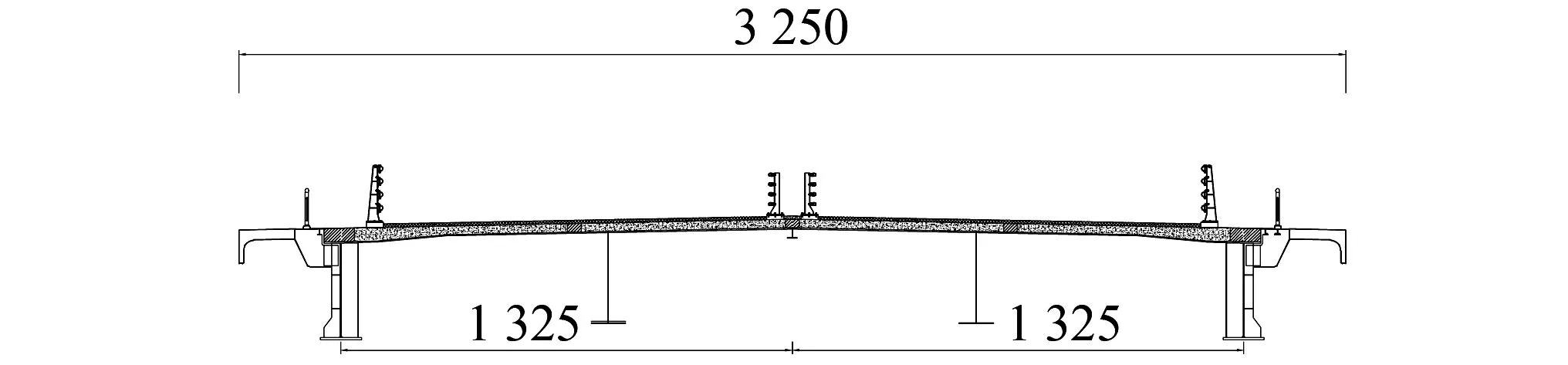
图1 主梁横断面示意图(cm)

为分析该斜拉桥各个施工阶段的静风稳定性发展规律,本文选取桥梁的最大双悬臂阶段、最大单悬臂阶段、中跨合龙阶段以及成桥阶段进行分析计算。图2表示该桥各个施工阶段的有限元模型,该模型采用单主梁模型进行模拟。主梁、桥塔按照欧拉—伯努利梁考虑,斜拉索按空间单向受拉杆考虑,采用质量辅助单元MASS21模拟桥面系与栏杆的质量压重和惯性矩效应。在进行静风计算时,主梁考虑风荷载的阻力、升力、升力矩三个荷载分量,桥塔和拉索只考虑阻力且桥塔阻力系数按照JTG/T 3360-01—2018《公路桥梁抗风设计规范》表5.4.1选取,拉索阻力系数取0.7。本文横向变位取逆风向为正,竖向变位取向上为正;扭转角的正负取决于风攻角,初始风攻角为0。同时为便于对拉索进行分析,对全桥拉索进行编号。拉索编号和方向规定如图3所示。

图2 各典型工况有限元模型

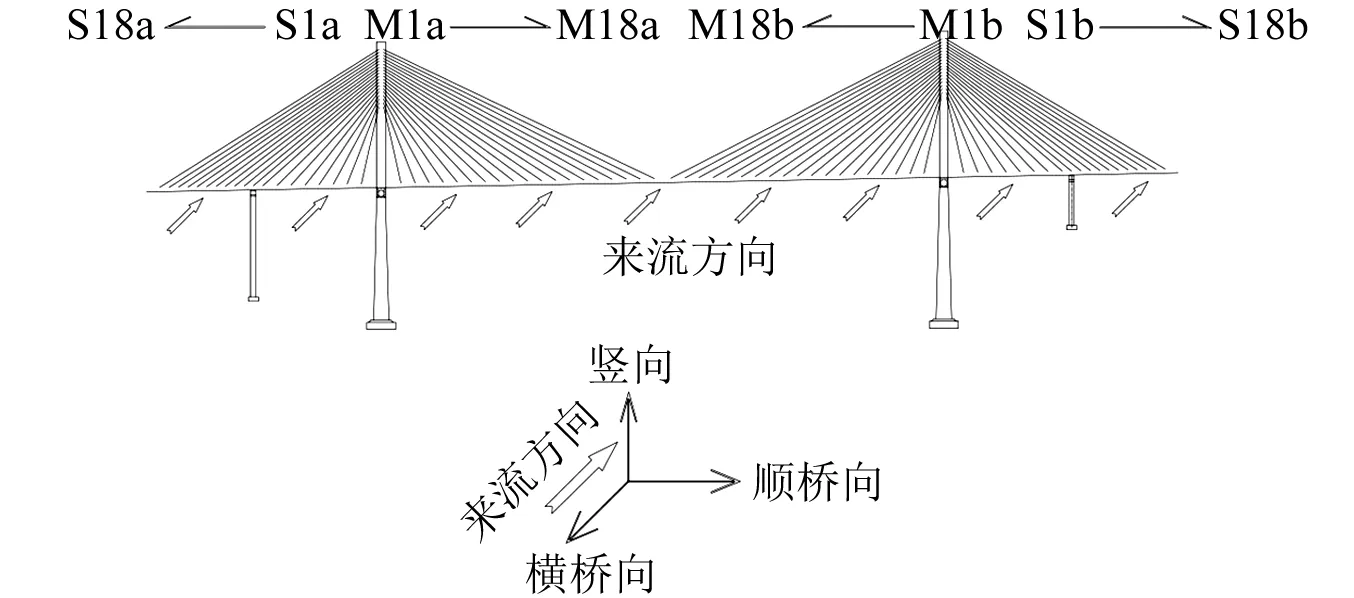
图3 全桥斜拉索编号

3.2 风洞试验测定三分力系数

为了计算不同空间姿态下结构所受到的静风荷载,进而分析结构静风响应,本研究按照1 ∶50的几何缩尺比制作主梁断面的节段模型,在长安大学CA—1风洞实验室利用杆式五分量应变天平进行主梁的静气动三分力系数测定。试验风攻角范围为-10°～10°,攻角增加步长为1°。试验节段模型如图4所示,所测得的三分力系数结果如图5所示。

图4 成桥阶段测力试验节段模型

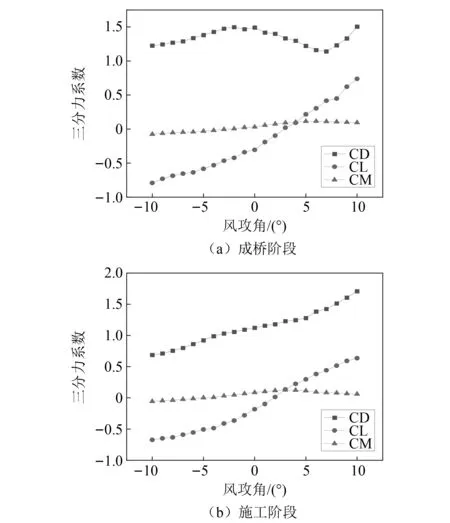
图5 主梁三分力系数

3 桥梁各阶段静风稳定性分析

3.1 静风失稳风速变化

对结构的四个典型工况进行静风稳定性计算分析,结果如图6所示。最大单悬臂状态为施工过程中的最不利工况,其失稳风速仅为72 m/s,且主梁跨中部位变位在各个典型工况中最大。图7列出了各个典型工况关键节点变位的发展路径。

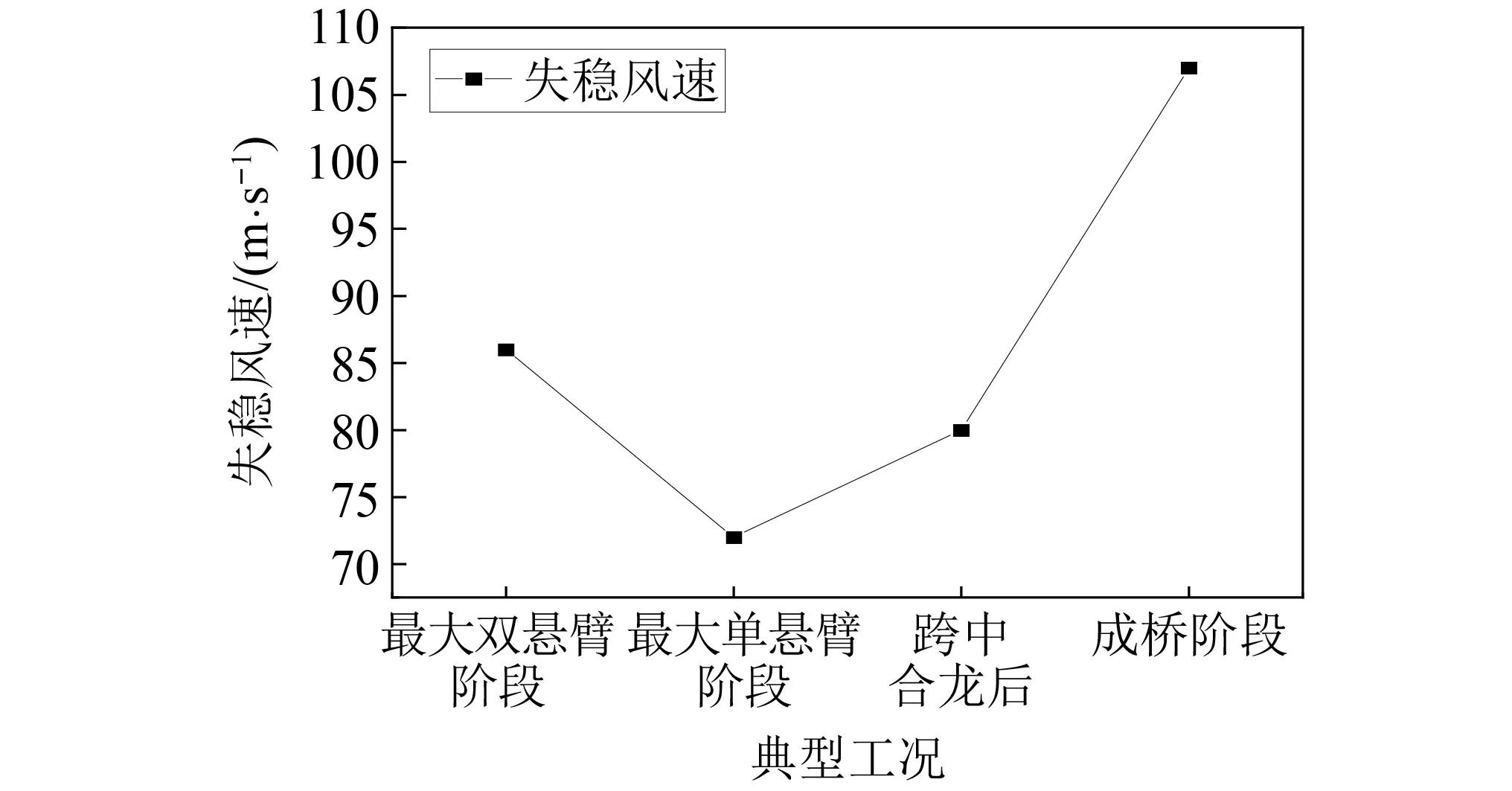
图6 各典型阶段失稳风速

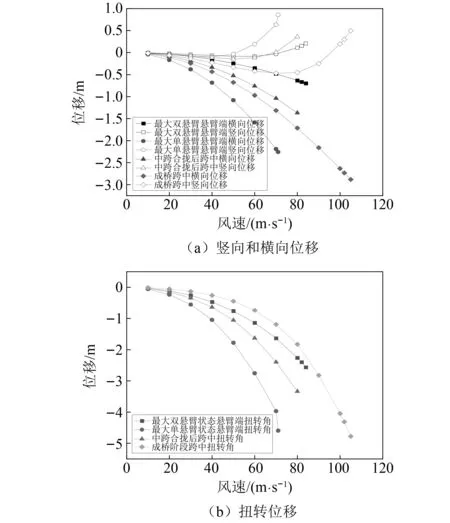
图7 主梁各施工阶段关键点位移

上述计算结果表明,随风速增加,各施工阶段主梁跨中或悬臂端位移均呈增大趋势,且风速越大,变形增加速度越大,接近失稳风速时,增速达到峰值。此外,不同施工阶段静风响应还有如下不同:

(1)在主跨未合龙之前,最大单悬臂状态比最大双悬臂状态更不利,结构失稳临界风速更小,梁端位移更大且发散趋势更明显、更突然。这是由于悬臂长度随着施工的进度而逐渐伸长,悬臂部分刚度减小,使其位移响应更大。

(2)主跨合龙使结构发生了体系转换。与最大单悬臂阶段相比,主梁跨中部位三个方向的变形均有大幅度下降,竖向变位和横向变位分别下降了58.1%和39.3%,扭转角下降了27.4%。

(3)成桥状态由于栏杆改变了主梁断面气动外形以及桥面系的质量作用,静风稳定性能大大增加,失稳风速较跨中合龙后提升了33.75%。

3.2 结构位移发展

刘黎阳等指出,低扭转刚度悬索桥在达到临界风速之前加劲梁变形基本是完全对称的,但是在达到临界风速之后,可能会出现加劲梁反向扭转,两四分点的扭转和竖向变位会出现随机分岔反向交替现象。为了探究低扭转刚度斜拉桥的位移发展,追踪了各典型工况下的主梁位移。图8～图11列出了在施工过程中各个阶段主梁主跨 (最大双悬臂包含边跨)位移的静风发展路径。

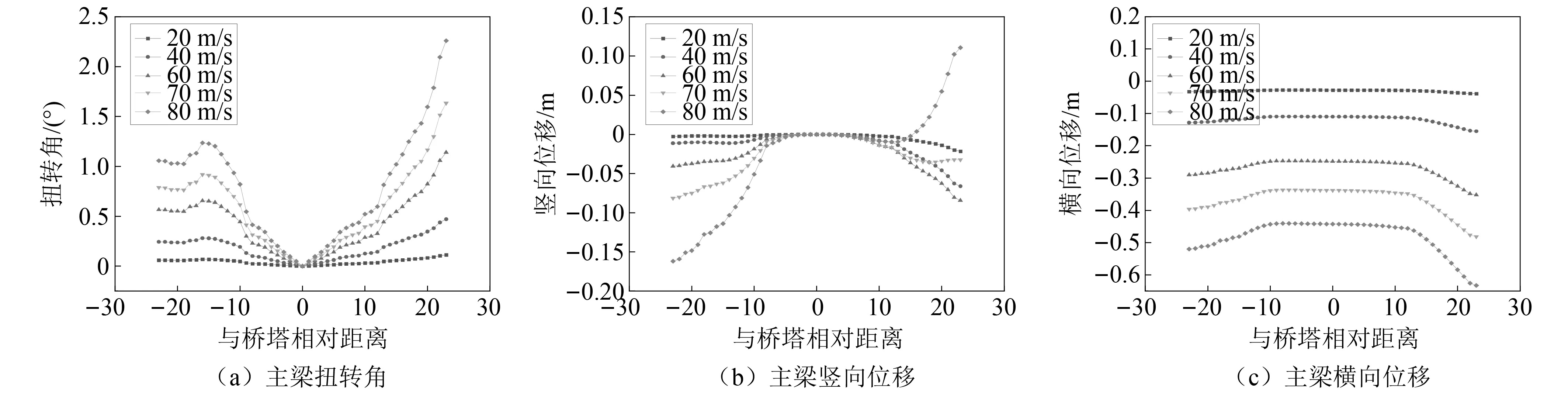
图8 最大双悬臂阶段主梁变位

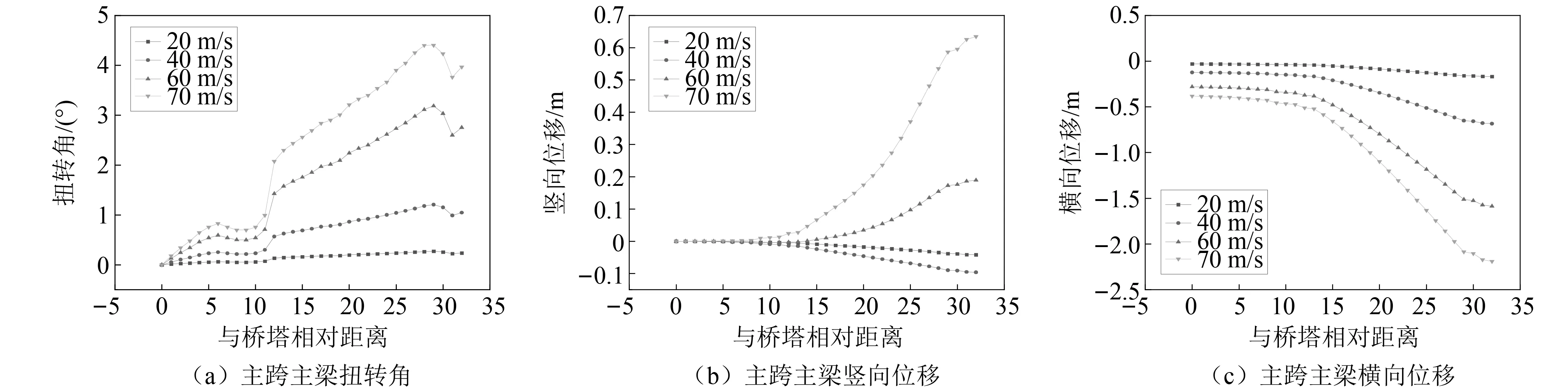
图9 最大单悬臂阶段主跨主梁变位

图10 跨中合龙后主梁变位

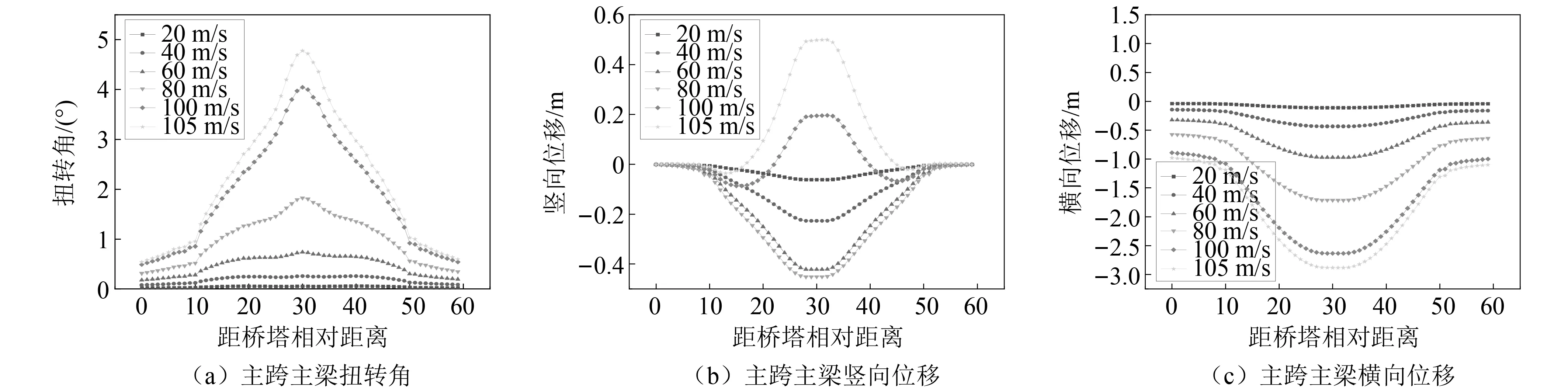
图11 成桥阶段主梁变位

在本桥算例中:①主跨扭转角均使结构与来流风呈正攻角;横向位移均为负值,而竖向位移在风速较小时向下变位,且随风速的增大而增大;在靠近失稳风速后,主跨四分点到跨中部位出现了类似低扭转刚度悬索桥的反向跳跃现象,结构迅速变为向上变位。随着施工阶段的发展,主梁失稳路径和空间姿态并未出现显著变化。②主梁对于静风荷载的敏感部位是基本一致的,跨中和悬臂端是结构静风荷载响应的最主要部位。跨中位移幅值远大于其他部位。③静风失稳形态是三向结构变位的复杂耦合现象,扭转位移、竖向位移和横向位移均有很大比重。④跨中合龙后主梁三个方向的响应均呈正对称,未出现四分点变位反向分岔交替现象。

3.3 失稳模式变化探究

在结构静风失稳过程中,扭转角、竖向变位、横向变位均占有很大比重。为进一步探究失稳过程中各个方向荷载分量主导程度和失稳模式的变化规律,从作用在结构上的风荷载和拉索体系的受力两方面对结构各典型工况进行分析,追踪各阶段结构在不同风速下的变化,以更深入地揭示静风失稳的机理。

3.3.1 结构风荷载变化

通过最大单悬臂阶段和成桥阶段跨中的风荷载阻力、升力和升力矩的发展趋势图(如图12和图13所示)可以发现,由于风荷载是风速的二次函数,作用在结构上的荷载随着风速的增大呈现抛物线趋势增长,这与结构在不同风速作用下的变位发展趋势是相一致的。此外,对比结构在初始攻角和变位后作用在结构上的风荷载,结构变位会令结构对风的敏感性大幅度提升,使作用在结构上的风荷载急剧增加;而急剧增加的风荷载又会大大加剧结构的非线性变形,导致结构迅速发生失稳而破坏。

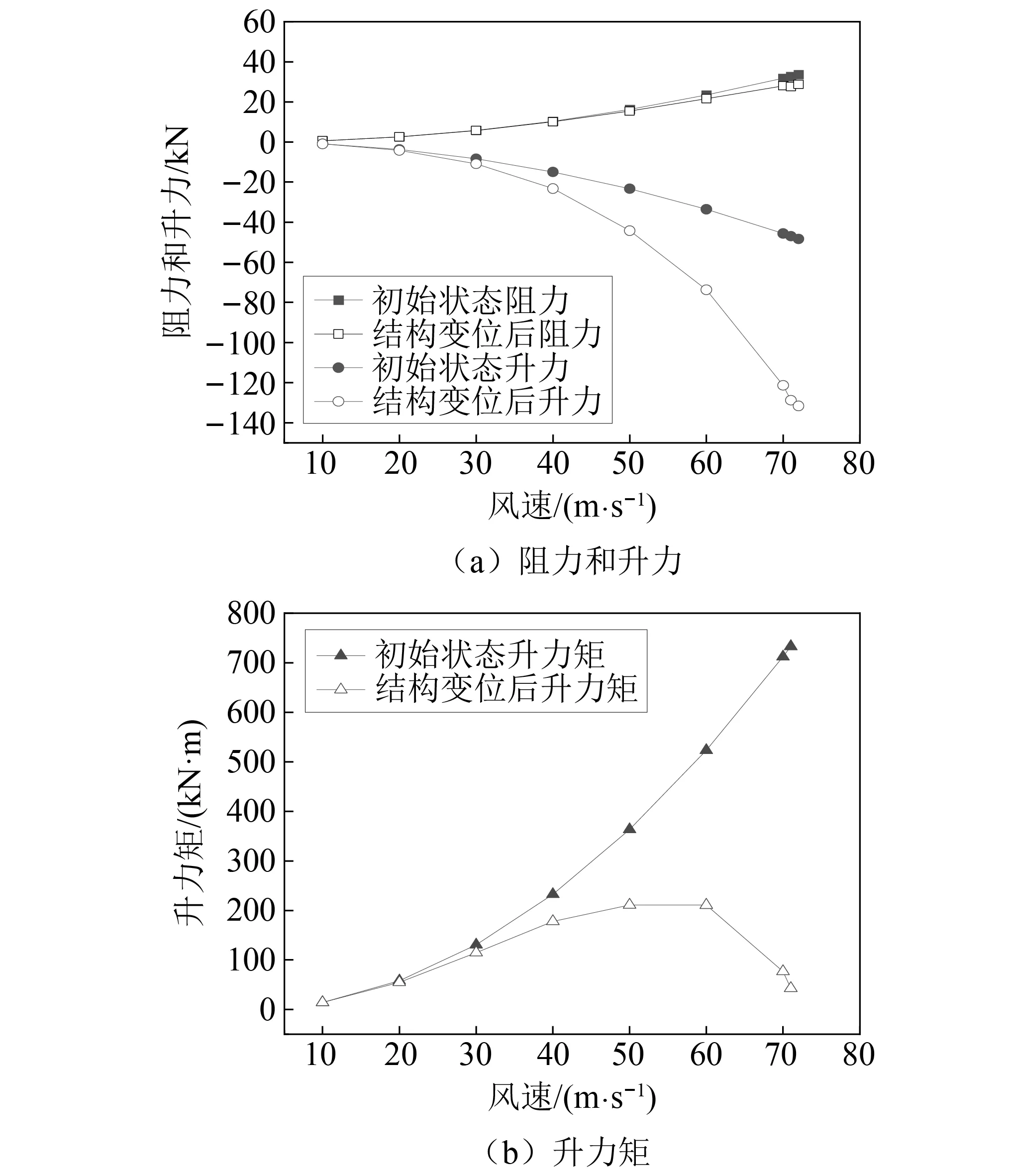
图12 最大单悬臂阶段主梁跨中三分力变化对比

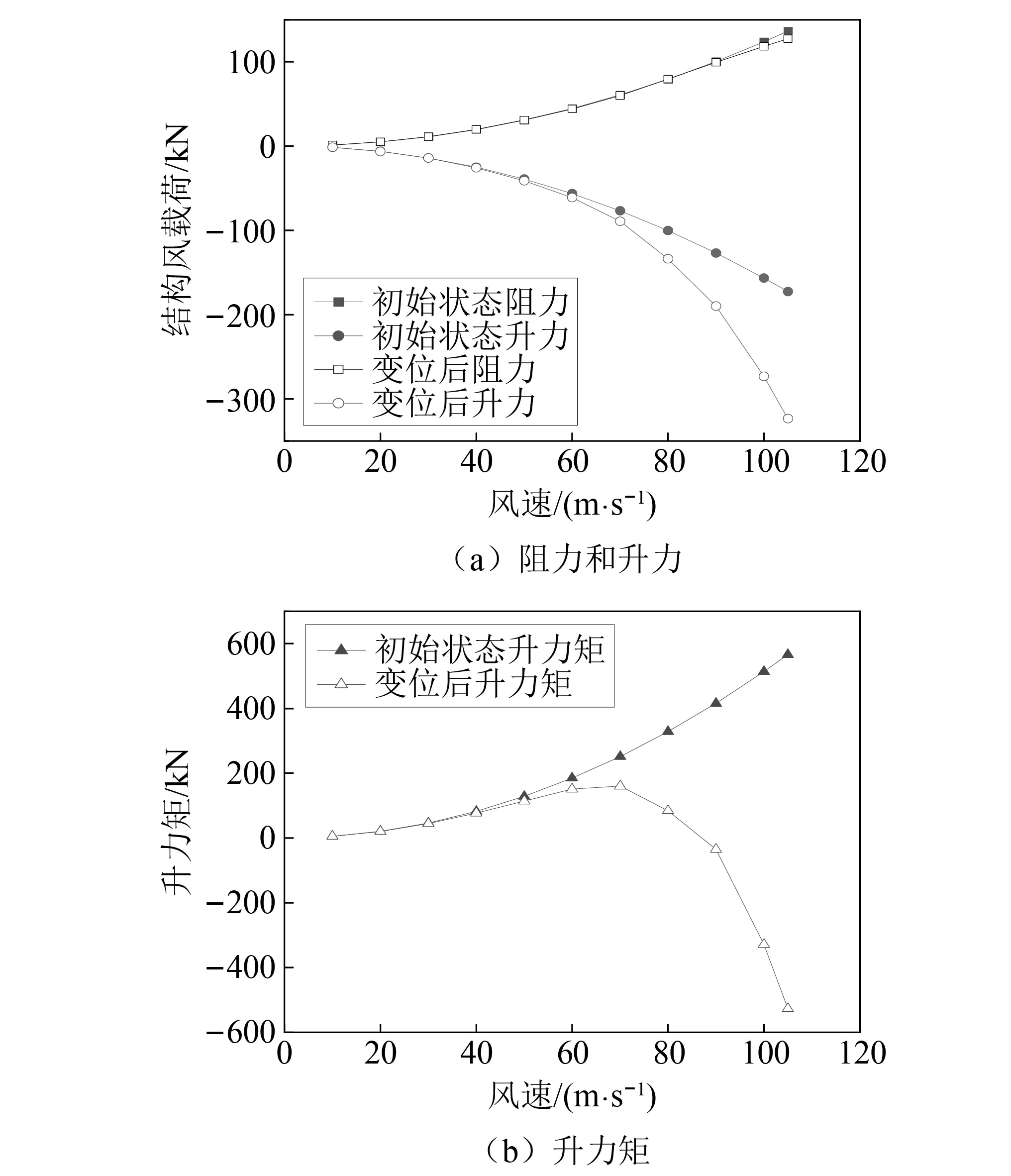
图13 成桥阶段主梁跨中三分力变化对比

从结构风荷载角度来看,结构各典型工况静风失稳主要为由升力和升力矩主导的竖向失稳和扭转失稳。利用风荷载分量的变化率可以清晰地表征结构对各风荷载分量的敏感程度。由表1可以发现,在风速达到1/2倍的失稳风速之后,结构对于风荷载的敏感性会大大增加。非线性变形明显加剧了结构所受到的升力,同时升力矩呈现更明显的非线性特征。在最大单悬臂阶段临近失稳风速时结构扭转角为-4.46°,此攻角下升力矩系数较小,大大减小了结构所承受的升力矩;而成桥状态下临近失稳风速时扭转角为-4.77°,升力矩急剧反向但未见明显减小。由此可见在结构建造运营过程中静风失稳模式发生了一定变化。

表1 成桥阶段主梁跨中三分力

3.3.2 拉索索力变化

斜拉桥拉索的作用是在主梁跨径范围内提供多个弹性支承,将主梁所承受的荷载传递给桥塔和下部结构,因此斜拉索是斜拉桥静风稳定计算的重要部分,通过拉索索力的变化可以清晰直观地反映结构静风位移发展路径和不同施工阶段失稳模式的变化。

由于跨中部分是成桥阶段主梁变位的主要部位,验算跨中部位的拉索应力变化能够较好的反映拉索在不同风速作用下的反应。图14为拉索M18a应力随风速变化的发展路径,表2列出了不同风速下拉索的应力值。可以发现,在风速很小的时候,跨中部位拉索应力随着风速的增大略微有所增大;当风速较大时,由于主梁扭转变形明显,迎风侧拉索应力首先开始减小且迅速降低;随后背风侧拉索的应力在接近失稳风速时开始降低,此时迎风侧拉索失效,应力降至0。

表2 成桥M18a拉索静风应力

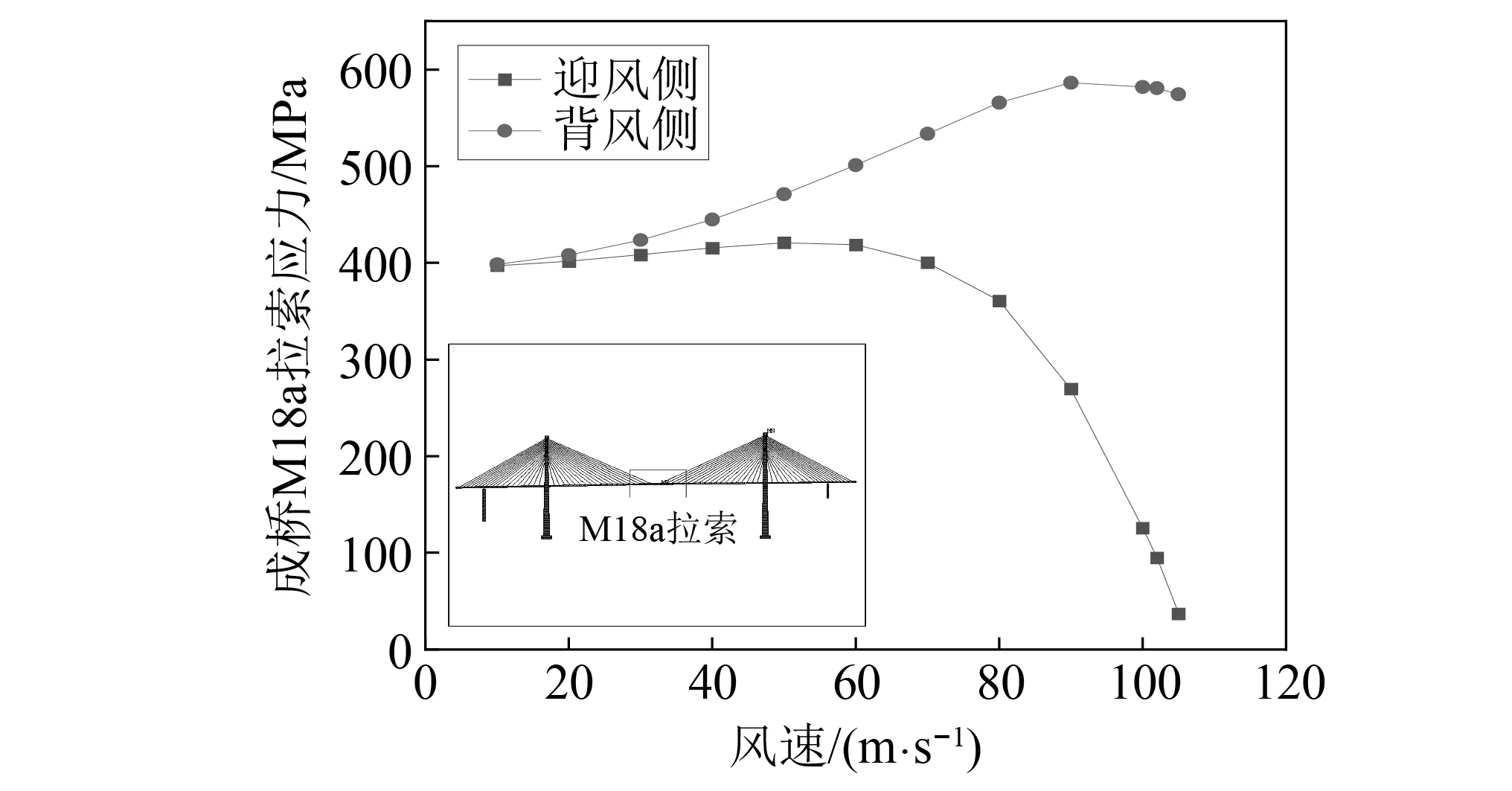
图14 成桥M18a拉索静风应力变化

引入拉索应力变化率,令

拉索应力变化率=应力变化率能清晰反映出拉索在不同风速下的工作状态,从而揭示拉索的失稳模式。迎风侧拉索与背风侧拉索索力发展截然不同,失稳模态表现出以升力矩为主导的扭转失稳。当风速小于50 m/s时,拉索均处于正常工作范围。当风速为105 m/s时,迎风侧拉索由于过大的变形应力明显降低,不足原先的10%,拉索已经完全失效。

(4)

继续追踪各典型工况失稳时拉索索力,结果如图15所示。发现失稳主要部位均在跨中和悬臂端,但失稳模式在施工过程中发生了转变,最大双悬臂阶段主梁静风失稳主要以竖向失稳为主,迎风侧、背风侧拉索索力基本一致而最大单悬臂阶段、跨中合龙及成桥状态均以扭转失稳为主。这是由于随着施工结构体系的改变结构的竖向刚度明显大于扭转刚度,使得扭转失稳模式占据主导。

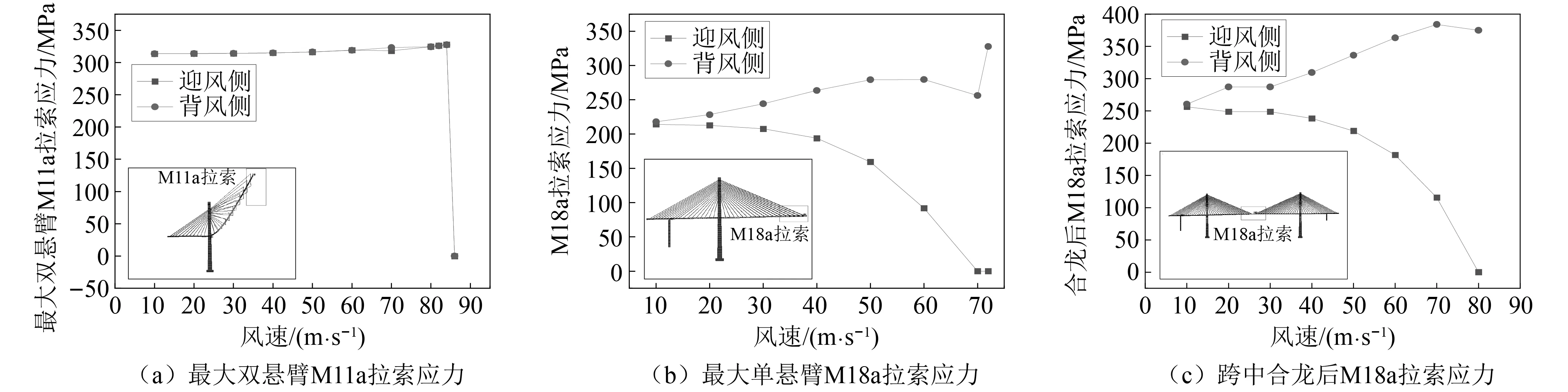
图15 施工阶段各典型工况拉索应力

3.4 不同施工完成率下的静风稳定性变化

在最大双悬臂施工至最大单悬臂的过程中,静风失稳模式由以竖向位移为主的失稳转变为以扭转为主的失稳形式。为深入探究该段施工过程中各个阶段失稳模式的变化,计算了单悬臂伸长过程中的静风稳定性能和失稳模式变化。毋庸置疑的是,随着悬臂的伸长,结构的失稳风速越来越低,这与本例的计算结果是一致的,其结果如图16所示。图中施工完成率为0时表示最大双悬臂发生结构体系转换变为单悬臂的状态,悬臂施工完成率100%代表最大单悬臂状态,不同的施工完成率代表了悬臂伸长的程度。

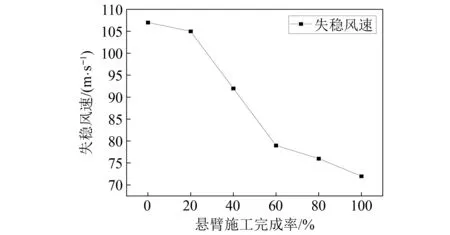
图16 单悬臂施工阶段失稳风速变化

对结构拉索索力进行分析,结果如图17所示。

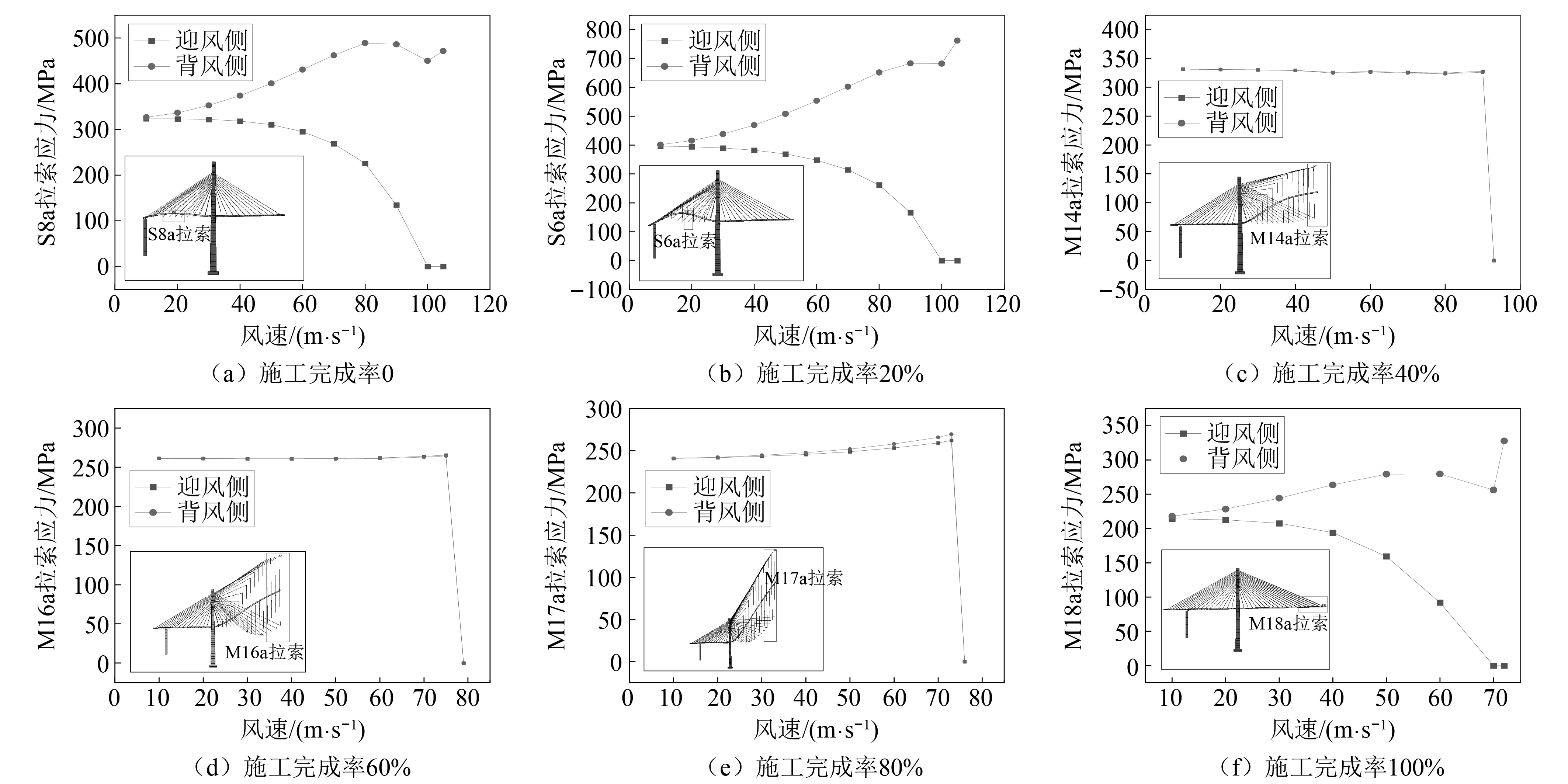
图17 不同悬臂施工完成率下失稳部位拉索应力

在单悬臂施工过程中,当悬臂施工完成率小于40%时,失稳形式主要在边跨跨中发生以扭转为主的失稳,主梁扭转幅度较大,此类失稳形式迎风侧拉索应力随风速增大逐渐减小,并在达到1/2失稳风速附近时迅速衰减,在接近失稳风速时降为0;背风侧拉索应力随风速增大而增大,在接近失稳风速时开始降低并发生应力突变。当悬臂施工完成率大于40%时,失稳部位转移到中跨悬臂端,失稳主要由竖向变位引起,同时伴随较大的扭转和横向位移。这种失稳形式迎风侧与背风侧拉索应力变化接近一致,随着风速增加两侧拉索应力略微有所增加,在接近临界风速时迅速突变为0。在达到最大单悬臂状态时,失稳又以扭转变位为主。

3.5 静风失稳机理

作用在结构上的风荷载呈现非线性增加,在风速较大时增速较快,引起结构的非线性变位;结构的非线性变位又反过来增强结构承受的风荷载,使风荷载的非线性特征更加明显。结构变位令拉索的垂度及变形会导致弹性模量存在一定的损失和降低[27],拉索的应力急剧下降是导致结构整体失稳的重要表现,迎风侧拉索索力的显著变化导致结构刚度的迅速降低,使得结构残余刚度不足以抵消气动负刚度的增加。当风荷载发生极小的增量时,结构迅速失稳而发生破坏。

4 结 论

本文通过对一座低扭转刚度非对称斜拉桥不同施工阶段进行了静风响应和稳定性计算,通过上述计算结果可得出以下结论:

(1)随着施工阶段的发展,结构的静风失稳模式发生了由竖向变位主导到扭转位移主导的转变。最大双悬臂阶段为竖向变位主导,其余阶段为扭转为主的失稳。不同的失稳模式拉索的索力表现出截然不同的变化特征。但无论哪种失稳模式,其他两向变位均占较大比重。

(2)斜拉桥的静风失稳主要发生在主梁的跨中部位以及施工阶段的悬臂部分。桥塔非对称布置和主梁单向横坡的影响较小,只是使跨径内主梁最大位移点略微偏移跨中点,并不会改变主梁的正对称失稳模式。

(3)大跨度斜拉桥静风失稳过程为:随着风速的不断增大,作用在结构上的荷载呈现抛物线形式增加,使主梁变位非线性增大。其附加风攻角不断增大反过来加大了结构对风速增量的敏感性,使得结构上的风荷载急剧变化。靠近临界风速时主梁出现弯扭耦合现象,拉索在较大的主梁变位下发生应力水平下降导致结构突然被破坏。

(4)在悬臂端逐步伸长的施工过程中,由于悬臂端刚度与长度l的平方成反比,中跨悬臂端刚度迅速减小使得静风失稳部位从边跨跨中转移到中跨悬臂端;随着施工的进行,悬臂端压重作用愈加明显,会减缓主梁的竖向变位促使静风失稳模式由竖向失稳向扭转失稳变化。使失稳模式经历边跨扭转失稳→中跨竖向失稳→中跨扭转失稳的变化。

(5)大跨度斜拉桥静风失稳的内在机理为:随着风速增加,结构响应与荷载非线性增加。当主梁扭转角占主导时,迎风侧和背风侧位移不同导致两侧拉索受力不均匀,迎风侧拉索由于垂度变化开始卸力,卸力部分由背风侧拉索承担。当接近失稳风速时,静风失稳部位迎风侧拉索应力水平下降,纵桥向相邻拉索也逐渐松弛变形,结构刚度逐渐减小使结构破坏;当主梁竖向位移主导时,两侧拉索应力变化一致,最终由于结构变位过大导致整体刚度衰减,难以抵抗微小的风荷载增量而破坏导致位移急剧增大,拉索达到松弛而失效。