双频激励下微弯液压管道的非线性振动研究

范 鑫, 舒 送, 张俊宁, 肖 璐, 毛晓晔, 丁 虎

(1. 中国人民解放军第5720工厂,安徽 芜湖 241007; 2. 中国科学技术大学 精密机械与精密仪器系,合肥 230026; 3. 上海大学 力学与工程科学学院 上海市应用数学和力学研究所,上海 200444)

液压系统是机器、发动机、飞机和许多工程机械的重要组成部分[1-3]。它通常包含许多用于输送液体和提供压力的管道。由于其结构的复杂性、激励的多源性以及耦合的关联性,使得其在工作过程中极易出现管道系统共振。由于涉及输流管道的机械系统都辅有多个动力设备,多个设备配合运转成为管路系统的主要振动源,多个振动源工作用加快了管道的疲劳故障进程。因此,探究双频激励下管道非线性动力学行为,科学维系管道系统安全可靠运行,保障输流管在双频强激励环境下正常工作成为目前研究日益突出且至关重要的问题。

要深入研究管道非线性振动行为,需要考虑其自身的结构形状和材料性质。由于工作环境及其自身重力的影响,管道的结构参数将不可避免地发生变化。为了得到更准确的非线性振动响应结果,有必要考虑管道的初始形状。学者们研究了微弯管道的各种振动问题[4-6]。李宝辉等[7]采用波动法获得振动波的传播和反射矩阵,提出了曲管平面内振动固有频率的计算方法。谢孝文[8]采用分块矩阵法讨论了不同边界条件下曲管的振动特性。2021年,Oyelade等[9-10]考虑微弯黏弹性管道,研究了横向振动下输送加压流体非局部应变梯度的非线性力学行为。Li等[11]分析了具有不同类型初始构型的弯曲管道输送流体的平面运动。Zhou等[12-13]分析了具有微小几何缺陷的流体输送支承管的稳定性和动力学。袁嘉瑞等[14]首次建立了基于Timoshenko理论的微弯管模型。Zhai等[15]研究了弯曲梁结构在轴向载荷作用下的非线性振动。曹建华等[16]基于样条小波有限元法建立了沿轴线可伸长的非线性输流曲管。最近,微弯管道模型已发展到非平面型[17]以及超临界区域[18-19]。以上的研究均是对单源激励下微弯管道的振动研究。虽然基于单频激励的管道动力学研究能够更加容易的实现特定的研究目的,但未针对多频振动激励源之间的耦合作用进行研究,而这种多频激励在工程中是非常常见的。

随着系统的结构和工作环境的越来越复杂,多频多源激励引起的振动问题日益突显,并在多个领域备受关注。道路交通领域,Zhang等[20]在针对车-路相互作用关系研究中发现,路面的破坏部分因素是由于车辆作用于路面的载荷激励和路面的自身振动共同作用引起的。轨道交通领域,Wu等[21]在针对高速列车牵引传动系统某结构长期使用出现的疲劳问题研究中发现它是由多个宽频带激励之间的耦合导致。航空运输领域,航空发动机压气机转子叶片故障主要由机械激励和气动激励共同引起的[22]。然而,针对如此复杂的振动环境,为方便研究,多数学者将多频激励振动假定为多个单频激励的线性叠加,如Tan等[23-25],而忽略了多个激励间的振动耦合关系。但是仅依靠单频激励振动是不能解释管道的所有振动问题的。2021年,Gao等指出飞机液压系统发生的振动故障主要是由于流体的波动和机身恶劣的振动环境构成的多激励引起的。同年,汪博等[26]针对管道系统所表现的动力学特性及管道系统动力学优化的研究现状进行了总结,强调管道系统不仅承受着复杂的多激励问题,在多载荷激励下极易发生振动超限,诱发管道及卡箍产生裂纹等故障。从以上的研究工作来看,目前针对管道的多频激励振动问题研究相对较少。另外,由于管道的构形是复杂多样的,考虑管道微曲,受传递路径和介质的影响,即便是同一激励到达管道不同位置产生的振动也会有所不同。以多频激励研究管道的振动问题不仅是紧跟当前管道系统发展的趋势,而且还是保障发动机乃至航空航天结构安全可靠运行的必然要求。本文从简单的双频激励出发,研究双频激励发生时管道的非线性振动特性。

本文针对固支液压管道考虑管道的微弯曲建立了双频激励下的力学模型,运用Galerkin法(Galerkin method ,GM)将偏微分方程离散为一组非线性耦合常微分方程,并采用龙格库塔法对方程组进行数值求解,分析系统在双频激振耦合作用下液压管道的振动响应。

1 动力学建模

如图1所示,一段微曲的液压管道两端固支,支撑之间的距离为Lp,管道的外径和内径分别为D和d,管道的密度为ρp,杨氏模量为E,截面惯性矩为Ip,外激励考虑为沿管道轴向均匀分布周期激励,其表达式为F(t)=F0[cos(Ω1t)+ηcos(Ω1t)],其中η为激励分配系数。管道中充满了航空液压油,为简化理论模型,将液压油视为无黏度的不可压缩牛顿流体。根据这一假设,管道中各处的油压都是相同的,因此液压油的压力影响可以忽略不计。液压油的密度为ρf,液压油流速为 Г。表1给出了这些参数的值。

在理想条件下,管道在使用寿命期间将是直线形状的,但是考虑到制造缺陷和蠕变变形,管道可能会有初始的弯曲幅值。初始曲线的存在对于系统的动态特性影响很大,这里记初始弯曲曲线为Y(x)。忽略外阻尼以及重力效应,因为轴向运动很小,只考虑横向运动,使用广义哈密顿原理建立管道的控制方程。

设管道的弯曲变形为u(x,t),因此管道动能为

(1)

式中,Ap为管道的横截面面积。液压油沿管道流动的动能为

(2)

式中:Af为流体的横截面面积;x或t前的逗号为x或t的偏导数。基于哈密顿原理,考虑管道的势能为

δUp=∭VEεxδεxdV

(3)

式中:V为管道体积;εx为一个微元体在x方向上的应变,应变-位移关系为

(4)

考虑沿管道均布谐波力的虚功,管道控制方程经变分计算后如下

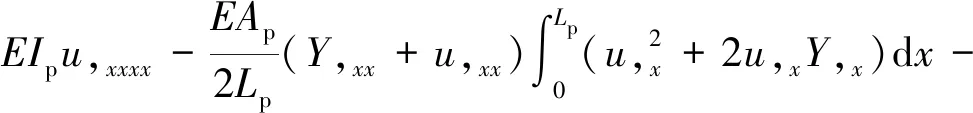
(5)

两端固定边界条件为

u(0,t)=0,u(Lp,t)=0,u,x(0,t)=0,u,x(Lp,t)=0

(6)

式中:F0为激励幅值;η为无量纲参数;Ω1和Ω2分别为两个不同的激励频率。

管道黏弹性用Kelvin物质导数描述,将以下本构关系[27]代入式(5)中

(7)

式中,μ为管道材料的黏弹性系数。代入后,液压管道控制方程为

(ρpAp+ρfAf)u,tt+2ρfAfΓu,xt+ρfAfΓ2u,xx+EIpu,xxxx+

F0[cos(Ω1t)+ηcos(Ω2t)]=0

(8)

其中,

(9)

考虑到边界条件为两端固定,可以使用以下函数来描述初始弯曲曲线

(10)

式中,A0为管道的初始弯曲幅值。

忽略外部激励、阻尼和控制方程中的非线性项,可以得到线性派生系统

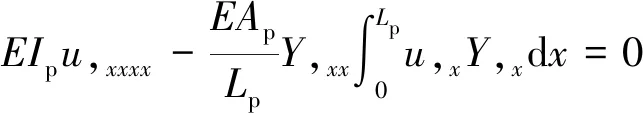
(11)

假设对应直梁的模态函数[28]为

φi(x)=C1icosβix+C2isinβix+C3icoshβix+C4isinhβix

(12)

将式(12)代入式(11)中可得

(13)

同样的,为保证式(13)有非零解,其系数矩阵行列式必须为 0,于是可以得到多个不同的特征值,即微曲液压管道的固有频率。对应于不同固有频率,从式(13)可以求得微曲液压管道近似模态。

根据Galerkin截断思想,将式(11)离散为具有N个广义坐标的常微分方程组。设解的形式如下

(14)

式中:φi(x)为从式(13)求得的模态函数;q=[q1,q2,q3,…,qn]T;φ=[φ1,φ2,φ3,…,φn]。

将式(14)代入控制方程式(8),在方程两边都乘以试函数φk(x),并且从0～Lp积分,可以得到N个常微分方程

fk[cos(Ω1t)+ηcos(Ω2t)]

(15)

为了便于研究受迫激励发生拍振时系统的振动响应,两个激振频率可以写成如式(16)所示的形式

Ω1=Ω+δΩ,Ω2=Ω-δΩ

(16)

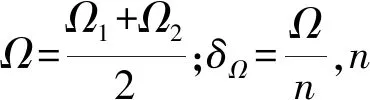
2 模型收敛性分析及验证

以流速121.5 m/s为例,图2 给出了不同Galerkin截断阶数下拱高变化时管道前两阶固有频率以及时域下管道中点位置横向运动的收敛性,其中外激励幅值和激励分配系数分别为F0=1 N/s,η=1。可以看出,四阶截断是收敛的,因此在后面的讨论中选择N=4。

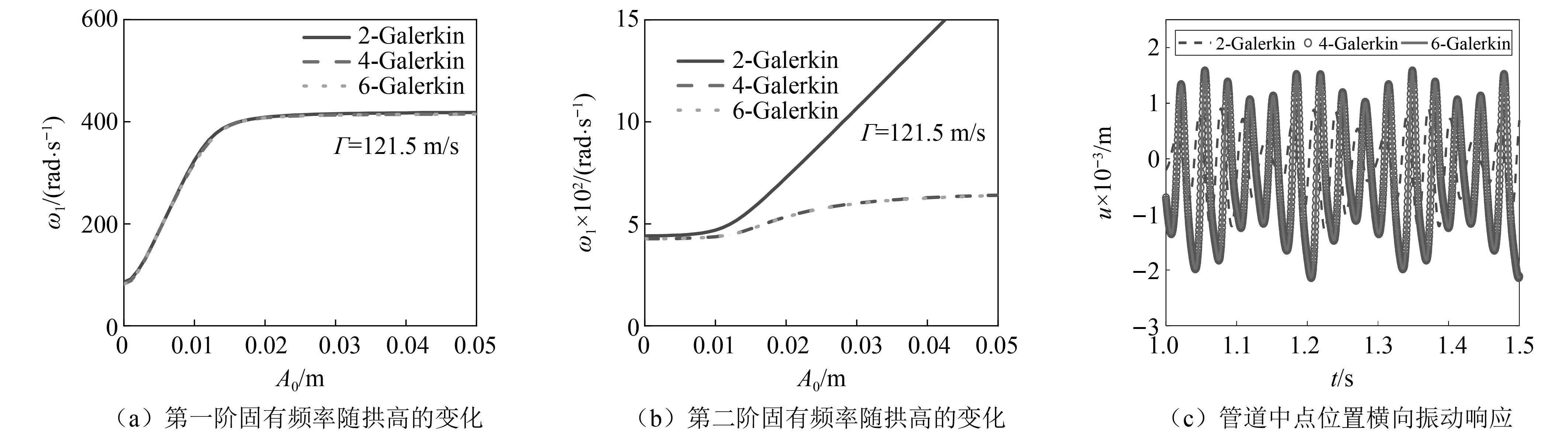
图2 连续模型Galerkin离散收敛性分析

另外,为了收敛离散模型的正确性,将GM与直接数值方法-微分求积单元法(differential quadrature element method,DQEM)进行了对比。对比结果如图3所示,两种方法的幅频仿真结果几乎完全重合,证实了四阶Galerkin截断系统可以在前两阶频率范围内精确表达原连续系统动力学特性。由此可见GM法作为一种模态离散方法,在关注模态频率范围内,有限自由度的截断便可以得到足够精确的动力学结果,且解在空间和时间上是连续的,因此广泛用于连续体动力学分析。而DQEM是一种空间离散方法,为得到收敛的高精度结果,需要对连续体进行多节点插值离散,计算方程较多,且仅在时间上连续。因此本工作中仅作为GM法的验证手段,而非主要研究手段。

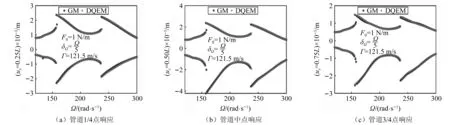
图3 四阶离散模型与连续模型精度对比

3 算例分析

图4分析了微弯液压管道在受迫双激励作用下频率离散系数取不同值时的幅频响应。由于频率离散系数n决定了激励频率差大小,n取值越大,频率差越小。由图4可见,随着频率差的减小,共振峰逐渐由两个峰合并成为了一个峰。不过,在此过程中,管道中点响应并非一直是周期响应。

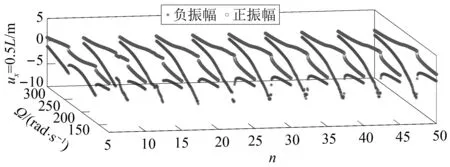
图4 双共振峰随激励频率差减小的合并演化过程

图5给出了当频率离散系数n=20时不同平均激励频率下管道中点位置的时域响应。易看出在双频激励作用下发生拍振现象。从周期性来看,图5(b)很难发现周期规律,而图5(a)和图5(c)是有一定的周期性的。

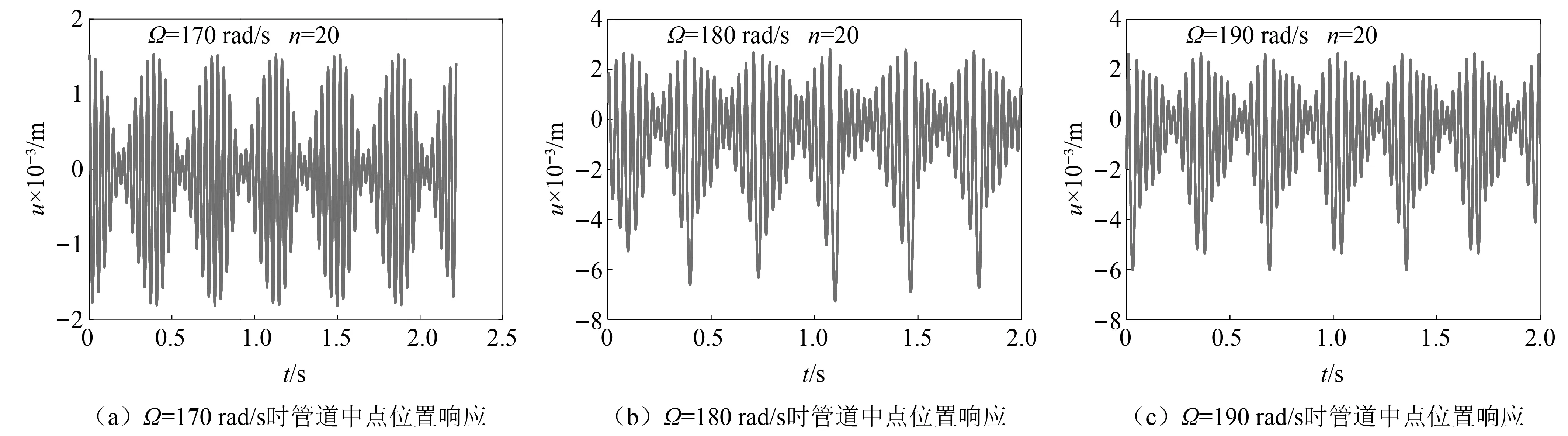
图5 Ω取不同值时管道中点位置的时域响应

图6 给出了频率离散系数n=20 时管道中点位置随激励平均频率Ω变化的分岔图,以及相对应的最大李亚普诺夫稳定性判定图,最大李亚普诺夫判定具体方法参考文献[29]。充分证实了Ω在 [178 181.7]存在混沌现象。

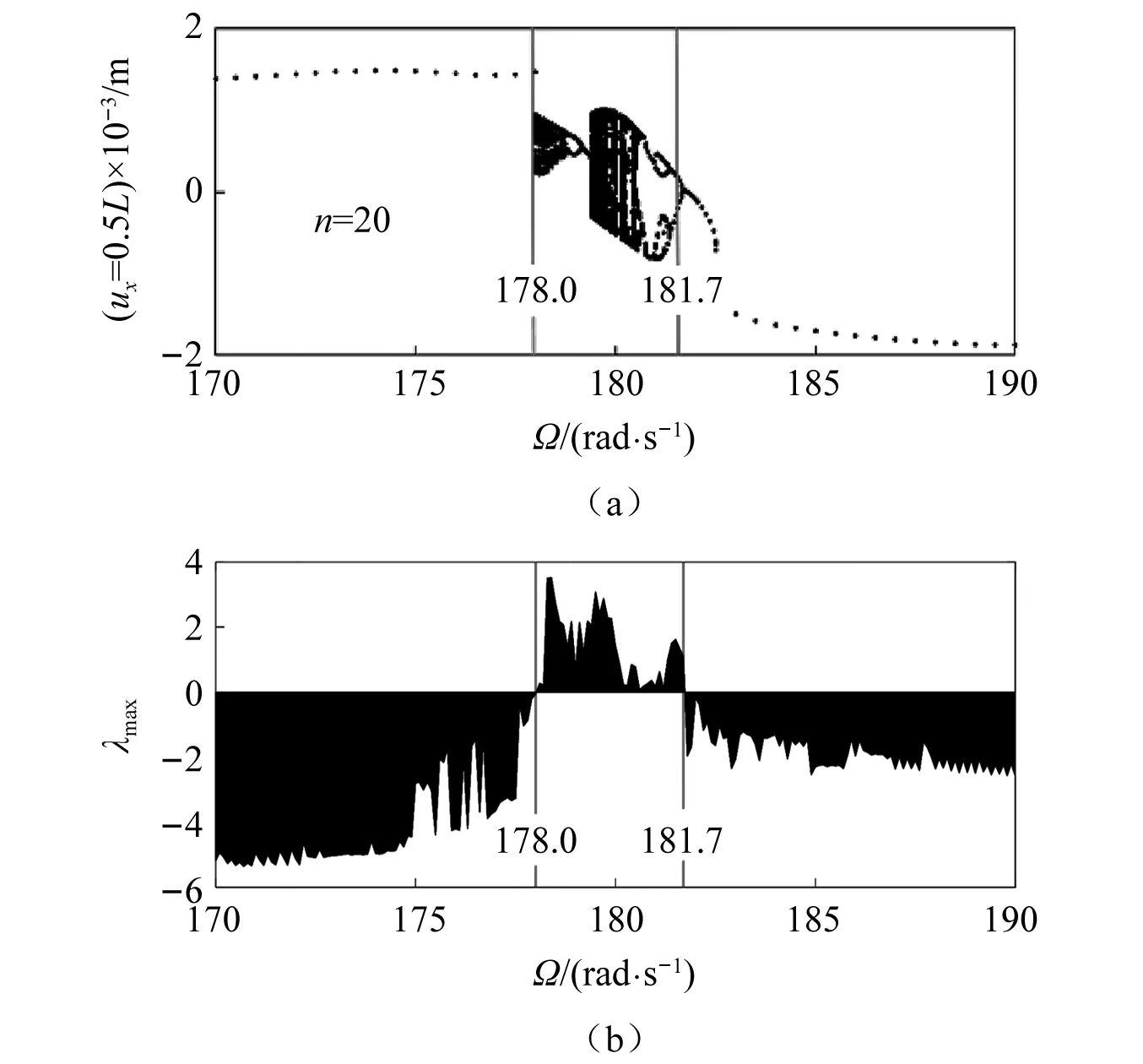
图6 n=20时管道最大李亚普诺夫稳定性判定

为了进一步说明系统振动随激励频率变化时存在非周期振动,图7给出了频率离散系数n分别为5,15,20,30,40和50时以Ω为分岔控制参数的分叉图。图中竖线区域内为会发生非周期振动的区间,从图的分析结果可以当n=5时,未出现混沌现象,如图7(a)所示;当n的取值分别为15,20,30,40时有明显混沌现象发生,且混沌发生区域呈先增大后减小的趋势,如图7(b)～ 图7(e)所示;当n=50时,发生混沌的区域变小,且混沌现象变弱,如图7(f)所示。

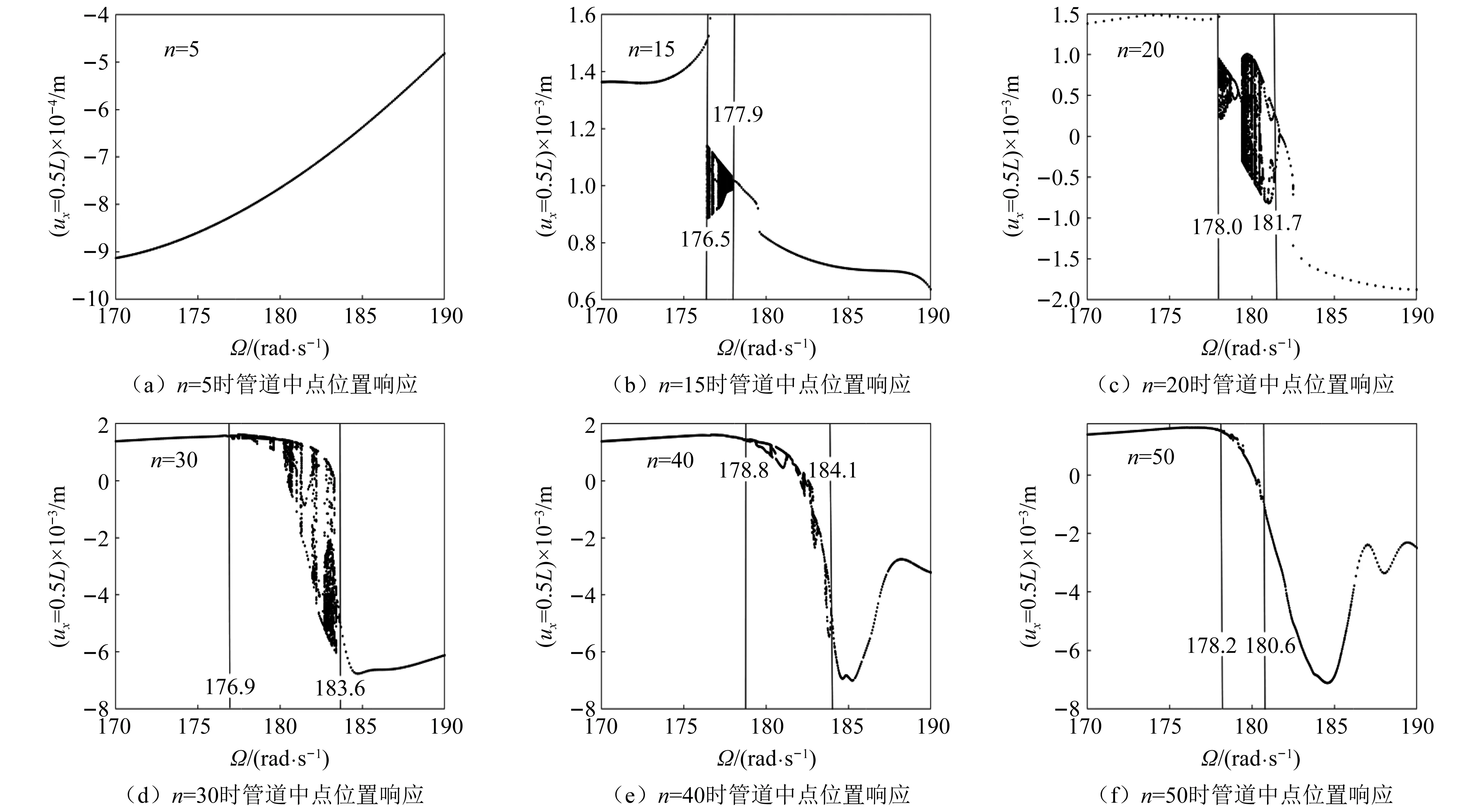
图7 以平均频率Ω为分岔控制参数的横向位移分叉图

结合图4和图7分析发现,由于n越大两个激励频率就会越相近,当两个频率差较大时(n较小时)不会发生混沌现象,随着两个频率的不断靠近(n不断增大)拍振现象出现,在共振频率附近出现混沌现象,且混沌区域也随之增大;当两个频率靠的越来越近时,混沌区域增大一定程度随之减小,混沌现象也变弱;从机理上分析,当两个频率差趋近于0时(n→∞),两个频率重合为单频激励。

4 结 论

本文讨论了双频激励耦合作用下微曲液压管道的非线性受迫振动问题,提出了以两个外激励频率平均值为研究对象进行微曲管道振动分析的分析方式,分析了两个激励频率差值对管道振动响应的影响,发现系统的分岔和混沌现象,得出如下结论:

(1) 微曲管道在周期双频受迫激励作用下,激振频率接近共振频率时,会发生强非周期振动。

(2) 随着两个激励频率差值的减小,共振峰由两个峰逐渐合成为一个峰。

(3) 两个激励频率相差较小时在共振附近会出现混沌现象,随着频率差值的减小,管道的混沌区域先增大后减小,混沌现象随之先增强后减弱。