高柔塔风电机组塔筒振动特性分析

何维令, 魏煜锋, 蒋祥增, 何宇翔

(明阳智慧能源集团股份公司 风能研究院,广东 中山 528437)

运行状态下风力发电机组同时受到外部环境载荷以及自身叶轮旋转载荷的耦合激励作用,使得机组的振动特性变得复杂。塔筒结构作为机组主要的支撑部件,具有轻质、高耸、低阻尼等特点,使得其对各种载荷激励的动力响应更为激烈,过大的振动不仅会对自身产生破坏作用,还会对机组的安全稳定性造成影响。因此,为保证机组能够正常运行,研究塔筒结构在运行状态下的振动规律和动态特性具有重要意义。

随着测试方法与信号处理技术的不断发展,基于现场原型观测数据来分析运行状态下风电机组塔筒结构的振动规律与动态特性越来越受到学者们的青睐。Hu等[1]对陆上5.0 MW风机塔筒的振动加速度信号进行连续监测,采用多参考最小二乘复频域法(poly reference least-squares complex frequency domain, p-LSCF)对风机的运行模态进行分析,发现了塔架基频与叶片过桨频率重合时导致机组共振的现象。赵艳[2]对海上1.5 MW风机塔筒结构的振动速度信号进行长时间的监测,采用随机子空间法(stochastic subspace identification, SSI)对塔筒进行模态参数识别,分析了自振频率、阻尼比随机组运行工况的变化规律并绘制了风机的共振校核图,最后基于Sommerfeld效应解释了风机在不同运行状态下振动现象。董霄峰等[3-4]对某海上风机塔筒结构的振动位移进行监测,讨论了机组在静止、启动、运行、停机以及极端台风工况下的塔筒结构振动响应规律以及振动安全性,并且基于谱峭度法、经验模态分解以及振动能量理论对不同运行工况下诱发结构振动的振源特性进行了分析。彭潜[5]基于腐蚀、倾斜、应力、土压力以及振动数据对海上某单桩式风机结构的健康状态进行评估,并给出了保障风机安全运行的合理化建议。

综上所述,目前业内学者对运行状态下风电机组的振动规律和动态特性的研究主要通过模态参数识别以及健康监测来实现,而对其在运行状态下的振动形式及其振动能量分布的研究较少,且研究对象主要为陆上和海上的钢塔结构,而对于高柔塔结构的研究鲜有报道。因此,为探究风电机组在不同工况下振动形式的变化特性以及振动信号能量的分布规律,本文以某140 m级高柔塔风电机组塔筒结构为研究对象,测量其不同高度处的振动响应信号,利用频谱分析方法分析其频域特性和振动形式,通过小波包分解和能量熵计算原理对实测信号进行分解和计算,得到塔筒结振动信号的能量分布特性和能量熵,并分析了两者之间的关系;最后对不同工况下各个测点振动信号的均方根 (root mean square, RMS) 值和能量熵进行统计,得到了高柔塔风电机组塔筒结构在运行状态下的不同振动形式及其振动能量强度和分布的变化规律,该研究成果对高柔塔风电机组的健康监测、安全评估以及塔架设计具有较高的实际运用和参考价值。

1 理论基础

1.1 小波包分解及能量计算

小波包分解已经广泛应用于各种信号处理过程中,它是以小波变换的一种信号分解精细算法,能实现对振动响应频带内的多层次均匀划分,不仅具有小波变换的信号低频部分精确分解的优点,还能同时对高频部分进行精确分解[6]。信号通过小波包分解后,信号的全部特征信息均得以保留,从而能大大提高信号分解的完整性[7]。

假定振动响应信号x(t)的最高频率为fmax,经过小波包的j层分解,可以得到2j个小波包系数[8],其表达式为

(1)

与这2j个小波包系数相对应的频带为[9]

(2)

将每个小波包系数进行重构可以得到对应的原始信号的小包能量

(3)

因此,原始信号可以分解为2j个小波包分量的和

(4)

对于原始振动响应信号x(t),j层小波包分解下的总能量Ex为[10]

(5)

利用小波包分解的正交性条件可以得到各个频段总能量为

(6)

式中,Ex为第i频段内的信号能量,其表达式为

(7)

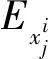
(8)

1.2 小波包能量熵计算

在信息论中,熵被用来衡量一个随机变量出现的期望值[11],是混乱程度的度量,在能量熵理论中,熵与信号或随机事件的不确定程度有关,可以反映系统频带能量比的变化情况[12],其表达式为

(9)

仅考察有两个能量比的能量熵函数[13]

(10)

令,η1+η2=k,(η1-η2)2=σ2且0<η1<η2,k<1,

(11)

(12)

当σ=0时,P(k,σ)取最大值,由此可以知道,当η1和η2越接近时,能量熵值越大;当二者相差越大,能量熵值越小。同样可以推广到式(9),当能量越趋于均匀分布时,能量熵值越大,当能量越趋于集中分布时,能量熵值越小。

风电机组在运行状态下随着叶轮转速的提升,塔筒振动信号的频谱和能量分布发生改变。低转速工况下时,塔筒结构主要受环境激励影响,信号能量主要分布在自振频率附近处;随着转速的提升,信号能量主要分布在叶轮的转频及其倍频处;当叶轮转频与塔筒固有频率接近或重合引起塔筒发生共振时,信号能量主要分布在共振频率处。这意味着,塔筒振动形式的变化,振动信号的频谱信息和能量分布也随着发生变化,引入能量熵值,能够很好的反映这种变化特性。

2 工程背景及实施方案

2.1 试验机组概况

试验机组采用为半直驱式的机组形式,位于河南省境内,属于低风速水平轴风力发电机机组,额定功率为3.0 MW,额定转速为11.1 r/min,风机叶轮直径为156 m,轮毂中心高度为140 m;塔筒为钢制锥筒结构,分为六节,每相邻两节之间通过高强度螺栓连接,从下到上各节的高度分别为17 m,17.5 m,22.5 m,25 m,27.5 m,27.42 m,塔筒总质量约为450 t,设计使用寿命为20年。

2.2 试验系统及方案

测试系统采用北京东方振动和噪声研究所研制的INV3068-S2数据采集仪以及中国地震局工程力学研究所研制的941B型低频速度拾振器。塔筒振动响应数据采集时,在每节塔筒顶部法兰处各设置一个测点,同时在各个测点的径向和法向各安装一个941B型低频拾振器,整个塔筒上自下共设置6个测点、安装12个拾振器。将各层传感器通过屏蔽线缆连接到塔基的采集器上进行数据测收集,其测点布置及传感器的安装示意图如图1所示。由于机组属于高柔、低频结构,因此将采样频率设置为12.8 Hz,采样时间设置为10 min/组。

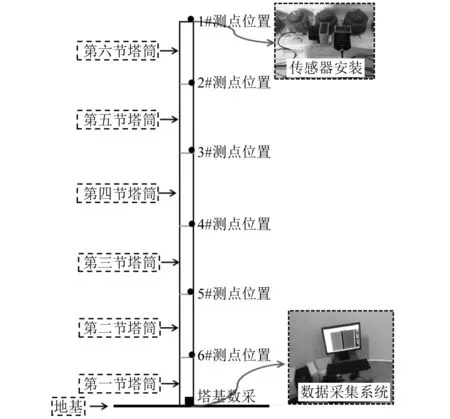
图1 测点布置示意图

2.3 试验分析流程

本文根据频谱分析和小波包分解及能量熵理论对运行状态下高柔塔风电机组塔筒结构的振动规律及动态特性进行分析,其流程如下:

步骤1对塔筒结构进行模态分析,了解塔筒结构的模态参数;

步骤2选取典型工况下塔筒结构的振动响应信号,通过频域分析了解信号的频谱特点,分析其振动形式;

步骤3运用小波包分解和能量熵计算原理对振动响应信号进行分解以及能量熵值的计算,确定塔筒振动信号的能量分布特性及其能量熵值的大小,并分析两者之间的关系;

步骤4计算振动信号的RMS值,以此代表塔筒振动的强度;

步骤5对不同工况下各测点的振动信号RMS值、能量熵进行统计,归纳总结塔筒结构在不同振动形式下其振动能量强度和分布的变化规律。

3 工程试验分析

3.1 模态分析

为了解塔筒结构的动态特性,开展其模态试验十分必要。图2给出了在停机工况下运用随机子空间模态参数识别算法的塔筒结构模态稳定图。图2中:‘.’为频率稳定;‘○’为频率、阻尼稳定;‘☆’为频率、阻尼比、振型三者都稳定;曲线为互功率谱曲线。其中,前两阶弯曲模态分别0.15 Hz,1.06 Hz,前两阶扭转模态分别为0.504 Hz,1.270 Hz[14]。

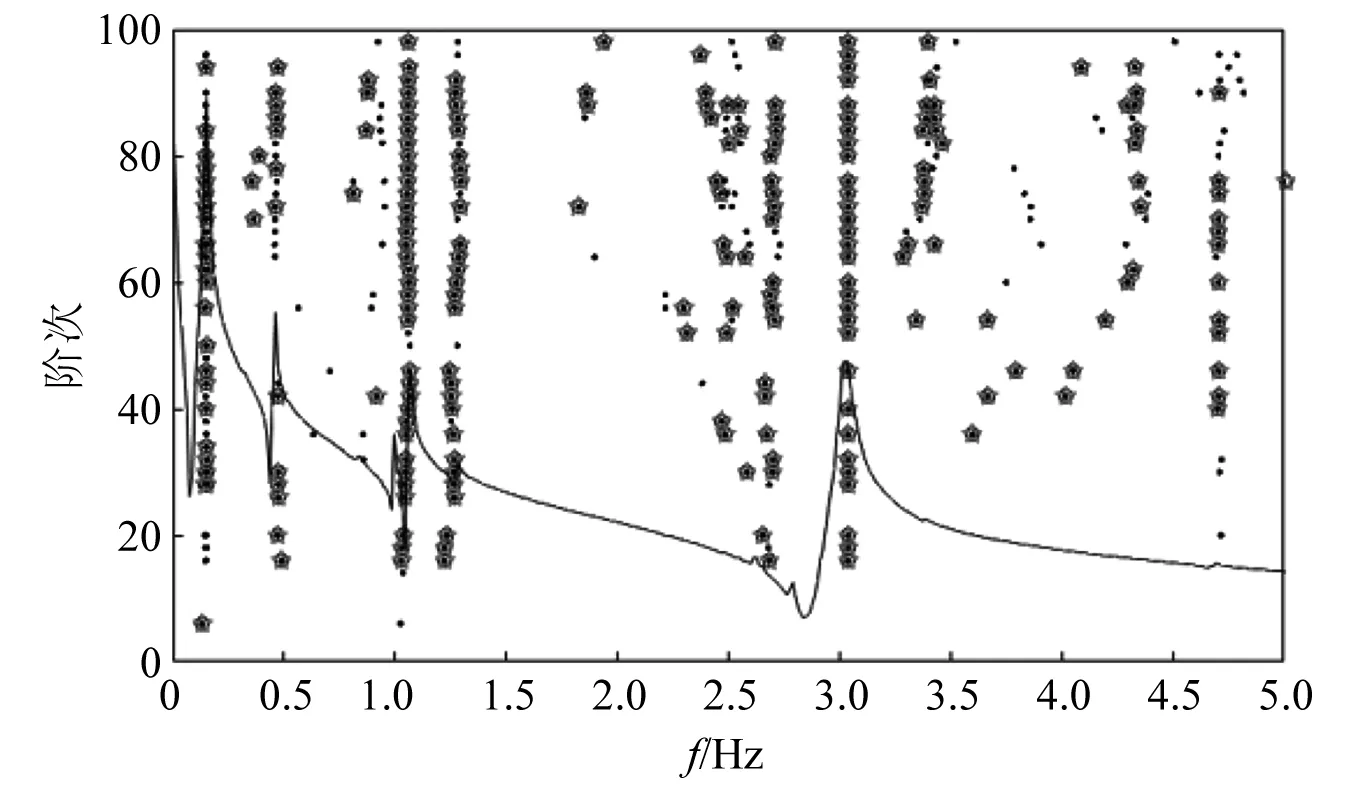
图2 塔筒模态稳定图

运行状态下,机组塔筒结构主要受环境激励和叶轮旋转激励的影响。低转速工况下,塔筒结构振动表现为自振形式,响应信号中的能量主要分布在一阶模态频率附近处;随着叶轮转速的提升,塔筒结构表现为强迫振动,响应信号中的能量主要分布在叶轮的转频及其倍频处;当叶轮转频及其倍频与塔筒的固有模态频率接近或重合时,结构发生共振,响应信号中的能量主要集中在模态频率附近。因此,塔筒结构的振动形式及其振动能量的分布与其模态参数密切相关。

3.2 振动响应分析

选取6种典型工况下的塔筒1#、3#、5#测点位置的振动响应信号进行时域和频域分析,其机组运行工况参数如表1所示。

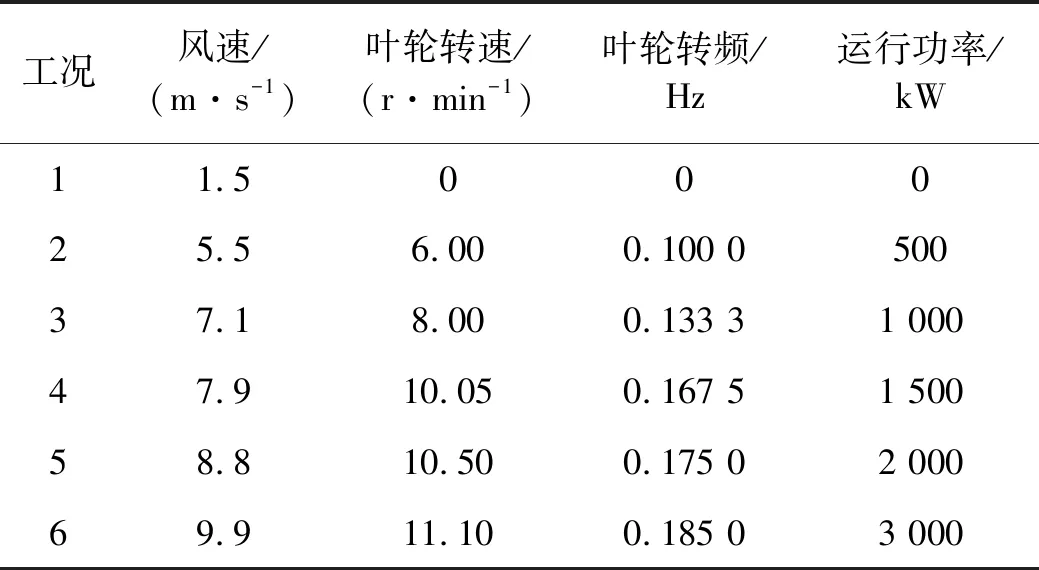
表1 6种工况参数表

图3给出6种典型工况下1#、3#、5#测点的振动响应时域和频谱图。图3(a)停机工况下振动响应幅值较小,频谱图中的3个测点频率信息主要体现为塔筒结构的一阶模态频率,此工况下塔筒结构完全受环境激励影响按一阶模态频率进行自振;图3(b)频谱图中3个测点优势频率体现为塔筒结构的一阶模态频率以及风轮的1倍频、3倍频、6倍频、9倍频以及塔筒的二阶弯曲以及二阶扭转模态频率,其中主导频率为塔筒的一阶自振频率以及风轮的转频,表明此工况下塔筒结构主要同时受其一阶自振和叶轮旋转的耦合激励作用,其振动形式表现为自振和强迫振动共存;图3(c)中的频谱分散,分布均匀,频率信息主要体现为叶轮的转频及其倍频成分,其一阶模态频率已经消失,表明此工况下,塔筒结构主要受叶轮旋转激励作用,其振动形式完全体现为强迫振动;图3(d)～图3(f)频谱图中,3个测点频率信息主要体现为风轮转频的1倍频、3倍频以及6倍频,其中在3倍频以及6倍频附近的频率峰值较为密集,形成分别以0.5 Hz和1.0 Hz为中心频率的共振带,对应塔筒结构的一阶扭转模态频率和二阶弯曲模态频率,对比时域幅值比其他3种工况下的幅值大得多,可知在此3种工况下,叶轮旋转的3倍频和6倍频与塔筒结构的固有模态频率接近或重合时导致塔筒发生了共振;从时域图和频谱图可以发现共振现象在3#测点处表现得十分突出,是由于该测点为塔筒结构的二阶弯曲模态位移最大位置,因次当风轮旋转6倍频与二阶弯曲模态频率接近或重合发生共振时3#测点的振动响应较其他测点要激烈;同时,由于风轮旋转激励为机组运行状态下的主要激励源,1#测点离风轮最近受风轮1倍频激励影响最大,因此频谱图中1#测点风轮1倍频信息表现最为突出、共振频率次之。由此可知塔筒结构在后3种工况下的振动形式体现为强迫振动与共振共存,且二阶弯曲共振起主导作用。

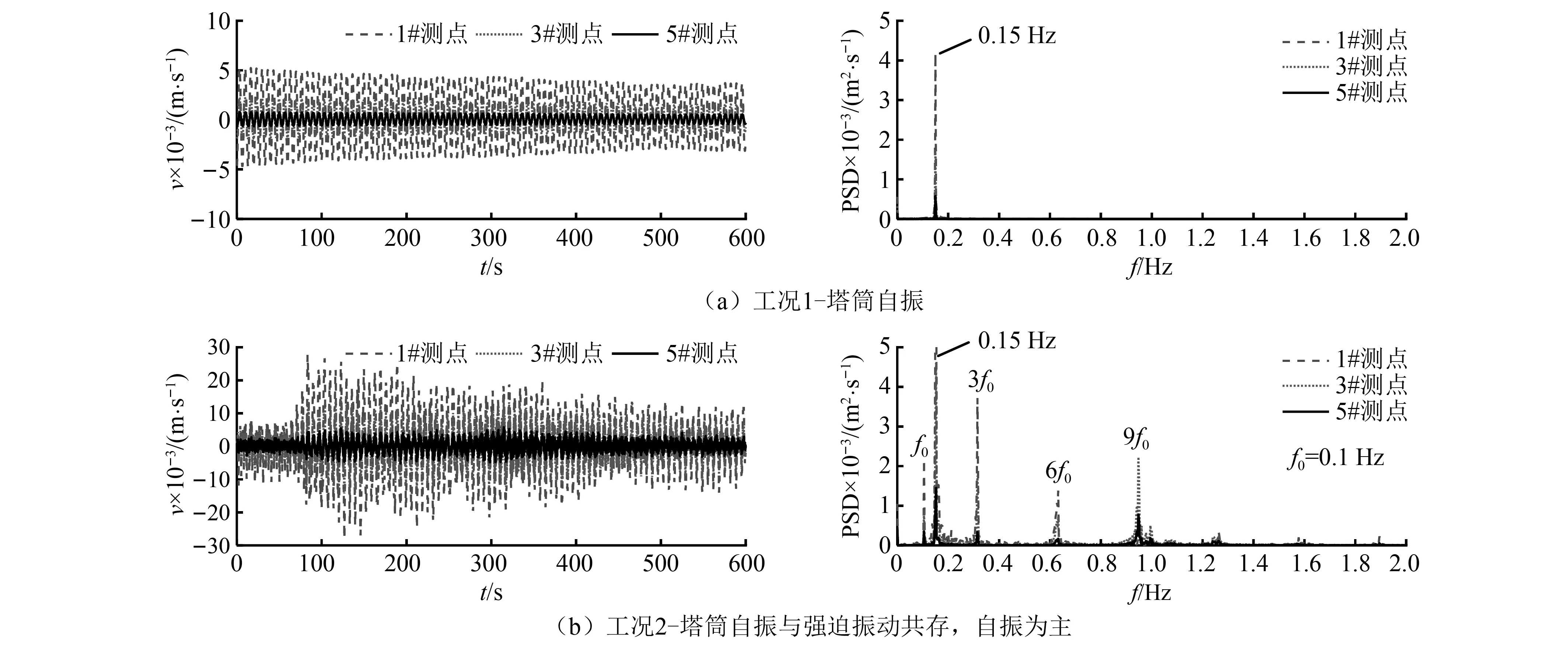
图3 典型工况下的塔筒振动响应时域和频谱图

3.3 小波包分解及能量熵计算

对6种工况数据进行小波包分解,由于塔筒振动响应信号具有周期性,因此小包函数选为sym5[15],分解层数为6,共分成64个子频带,测试时采样频率为12.8 Hz,根据采样定理[16],fmax=6.4 Hz,因此每个子频带的带宽为0.1 Hz。由于篇幅有限,表2只给出6种工况下3#测点位置振动信号小波包分解后各个子频带的能量占比及能量熵值,可以发现各个工况数据的能量主要集中在前32个子频带中,能量占比达到99%以上。其中工况1时,振动能量主要集中在第2个子频带中,对应频谱中的0.15 Hz,能量占比高达94.352%,其能量熵值为0.014 4;工况2时,振动能量主要分布在第2、第4、第7、第10个子频带中,对应频谱中的1倍频、3倍频、6倍频和9倍频,第2个子频带能量占比达49.034%,占主导优势,其能量熵值为0.8481;工况3时,振动能量分布区域较多,分别在第2、第3、第5、第9、第12、第16个子频带中,对应频谱中的1倍频、2倍频、3倍频、6倍频、9倍频、12倍频,且能量占比均匀,其能量熵值为1.272 6;工况4～工况5时,振动能量主要集中在3倍频和6倍频附近的子频带中,且在6倍频附近的子频带能量占比较大,但没工况1的第2频带能量占比大,其能量熵值分别为0.886 8,0.729 2,0.733 7。

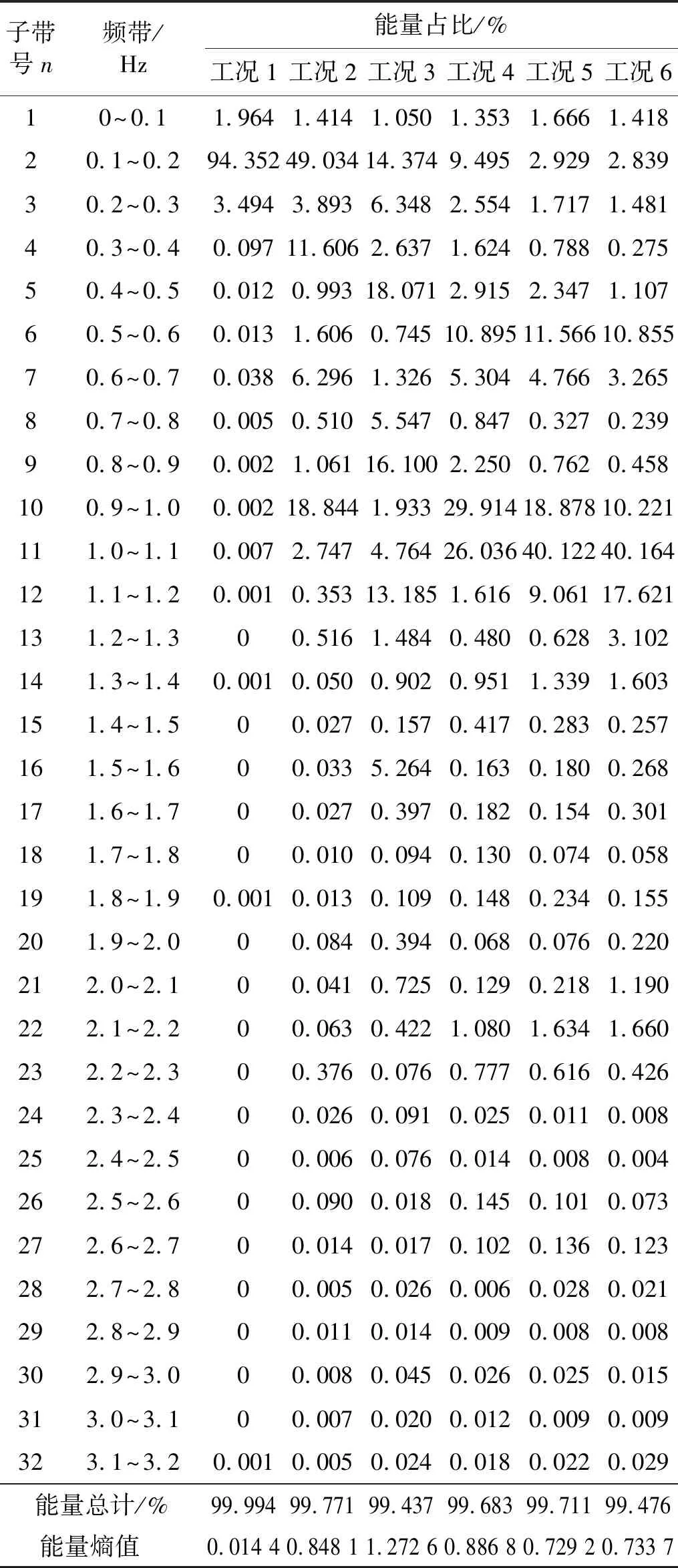
表2 6种工况小波包分解能量占比及能量熵统计表

从以上分析可以发现,振动能量熵值跟信号的能量分布有关,其中能量分布越集中且能量占越比大其小波包能量熵值越小;反之,能量分布及其能量占比越均匀,其小波包能量熵值越大。同时也可发现,随着叶轮转速的提升,塔筒振动能量集中的频率逐渐由从一阶模态频率到叶轮转频及倍频再到二阶模态频率发生改变。结合3.2节中的分析结果,塔筒振动能量的分布及其能量熵值的改变与其振动形式的改变具有密切的相关性:停机工况时,塔筒结构按其一阶自振频率进行自振,其振动能量主要分布在一阶频率附近处,能量分布较为集中,其能量熵值较小;随着叶轮转速的提升,塔筒结构的振动形式表现为受叶轮转频激励发生强迫振动,其振动能量主要集中在转频及其倍频附近处,能量分布较为均匀,其能量熵值越大;随着叶轮转速的进一步提升,当叶轮的倍频与塔筒结构的模态频率接近或重合时,塔筒结构发生共振,其振动能量主要分布在模态频率附近处,能量分布较为集中,其能量熵值较小。

4 塔筒振动强度及其能量分布特性分析

4.1 不同高度振动强度及其能量分布变化规律

图4给出6种典型工况下塔筒结构在不同高度处振动响应信号的RMS值、能量占比以及能量熵值。从图4(a)中可以发现:工况1到工况3时,塔筒振动响应随着高度的增加其振动响应RMS值越大;工况4～工况6时,塔筒振动响应RMS值为中间大两头小,其中RMS最大的为3#测点最小的为6#测点。图4(b)为6种工况不同高度处振动能量占比柱状图,振动能量占比较大的为工况4到工况6,且同一工况下,振动能量主要集中在中间部位,其中3#测点能量占比最大。图4(c)中,停机工况下各高度处的振动能量熵值较小,随着功率的提升,各个测点振动能量熵值变化规律不同,工况2、工况3随着塔筒高度的增加,其能量熵值逐渐减小;工况4～工况5,能量熵值呈现出中间小两头大的态势,其中能量熵值最小的为3#测点,能量熵值最大的为6#测点。

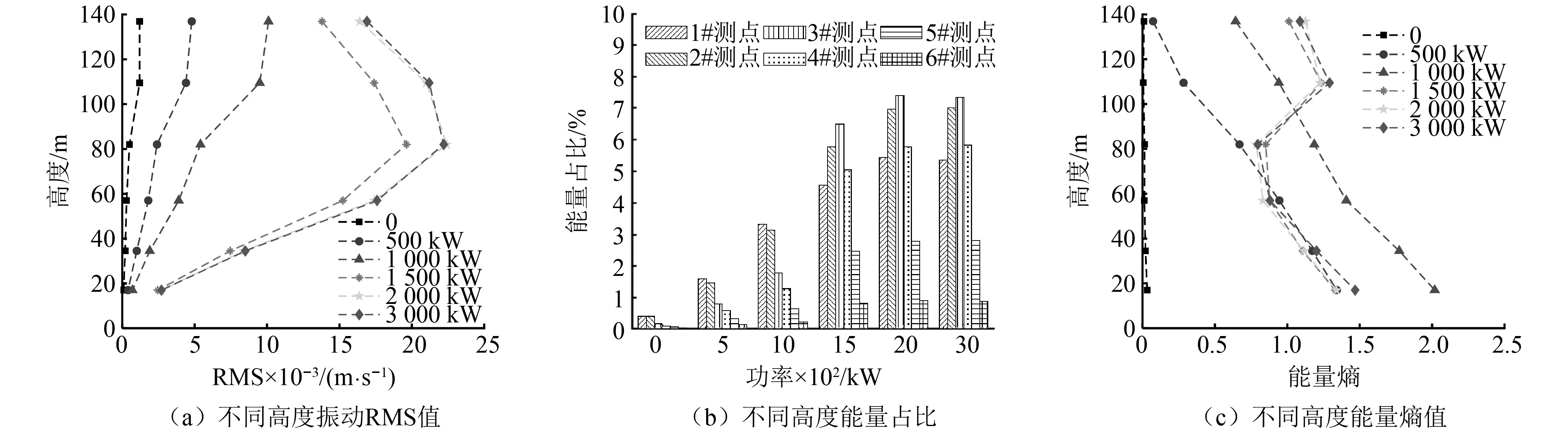
图4 典型工况下不同高度处塔筒振动的RMS值和能量占比及其能量熵值

以上分析表明,塔筒结构在不同高度处振动能量的强度和分布不同:针对前3种工况,随着测点位置的降低,塔筒振动强度逐渐减小,能量分布越不集中;针对后面3种工况,各个测点振动强度明显增强,且塔筒中间部位的振动强度及其集中度都高于两头。运行状态下,塔筒结构主要受叶轮旋转激励的作用,塔筒上部测点振动响应中的频率信息主要体现为叶轮1倍转频,因此相对于其他位置来说振动能量更为集中;下部测点能量分散除了其频率信息体现多个叶轮倍频外还可能是在风轮旋转激励或共振激励下诱发了塔筒结构的多阶固频振动所致,但该固频振动能量相对于叶轮转频和塔筒共振激励能量来说很小。

4.2 不同工况振动强度及其能量分布变化规律

图5给出塔筒结构1#、3#、5#测点振动响应RMS值随风速、叶轮转速以及发电功率的变化散点图及其拟合趋势曲线图。从图5中可以发现,随着风速、叶轮转速以及发电功率的增加,各个测点的振动RMS值具有增高的趋势;并且在低风速(风速<8 m/s)、低叶轮转速(<10 r/min)、低功率(功率<1 500 kW)工况下,塔筒结构随着高度的增加振动能量强度越大;但在高风速(风速>8 m/s)、高叶轮转速(>10 r/min)、高功率(功率>1 500 kW)工况下,中部位置测点的振动强度大于其他位置。同时可以发现,在图5(b)中可以发现风电机组在8.5～9.5 r/min之间设置了禁止转速区,使得叶轮转频有效的避开了塔筒一阶自振频率,实现机组塔筒的一阶共振穿越。

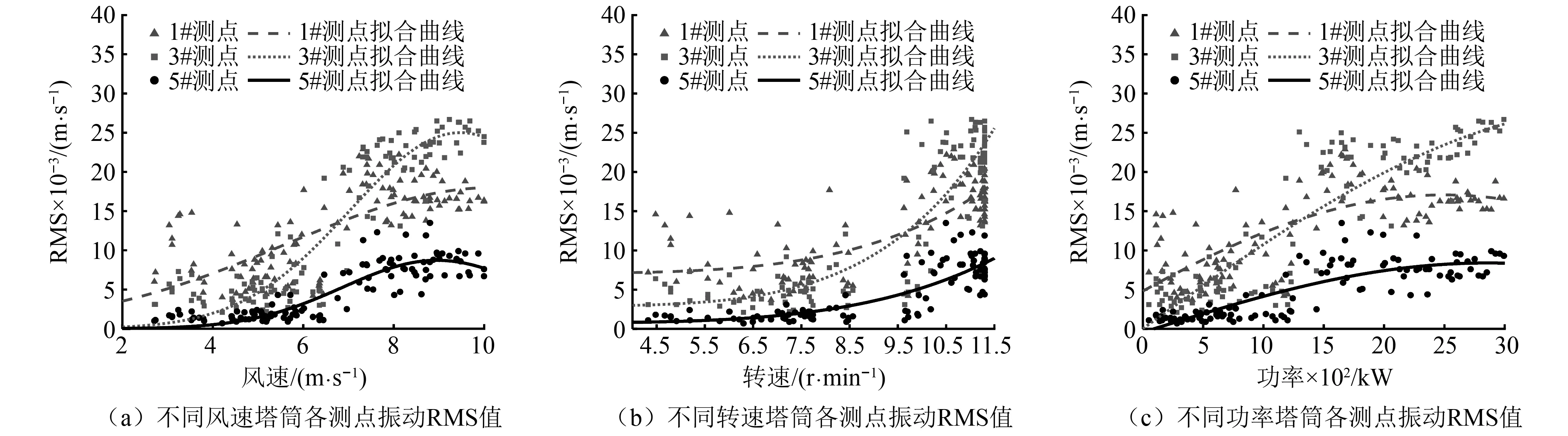
图5 振动RMS值随环境因素和运行因素的变化规律图

结合3.2节和4.1节的分析结果,柔塔机组在运行状态下,塔筒结构主要受叶轮旋转激励作用,低转速区,塔筒结构离叶轮越近其响应更激励振动能量越大,越远其响应越小振动能量越小;在高转速区,叶轮的6倍频与塔筒的二阶弯曲模态频率接近或重合时,导致其发生共振振动,其振动能量较大,由于6倍转频激起塔筒二阶共振,因此塔筒中部位置的振动强度强于其他位置,出现中间大两头小的趋势,呈现出如图4(a)所示的“二阶弯曲模态振型”。

图6为塔筒结构1#、3#、5#测点振动响应能量熵值随风速、叶轮转速以及发电功率的散点图及其拟合趋势图,从中可以发现,随着环境因素和机组运行因素的变化,塔筒各个测点振动能量熵值具有先增加后变小最后趋于平稳的趋势,底部5#测点的能量熵值普遍大于其他测点的能量熵;并且在低风速(风速<8 m/s)、低叶轮转速(<10 r/min)、低功率(功率<1 500 kW)工况下,3#测点的能量熵值大于1#测点的能量熵值,在高风速(风速>8 m/s)、高转速(>10 r/min)、高功率(功率>1 500 kW)工况下,3#测点的能量熵开始小于1#测点的能量熵值。

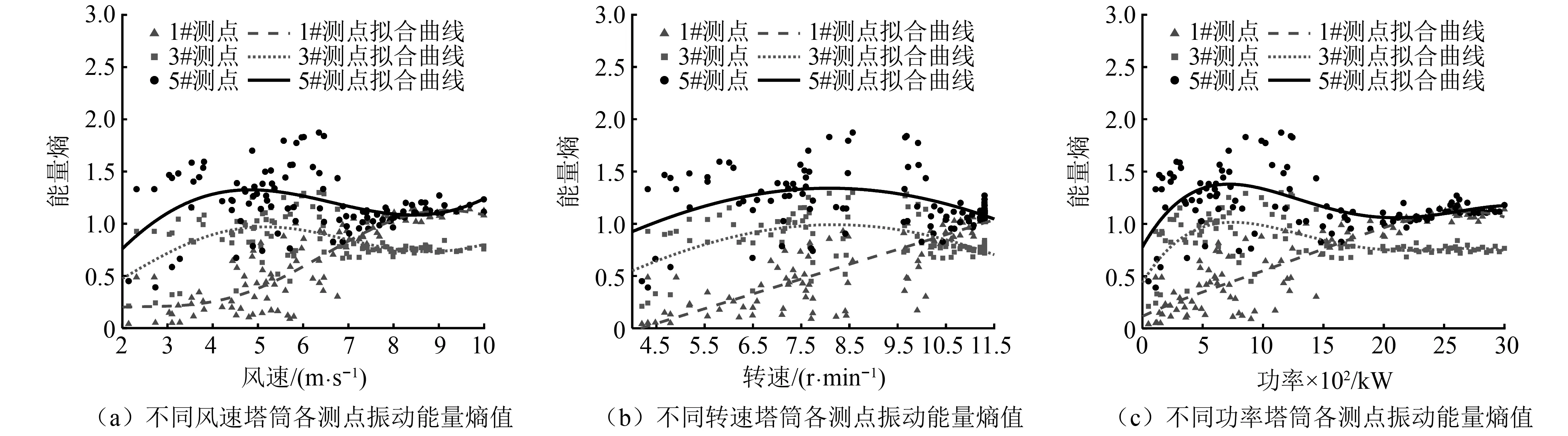
图6 振动能量熵值随环境因素和运行因素的变化规律图

低转速工况下,塔筒主要受其一阶自振激励影响,振动能量主要集中在一阶频率附近,其他频带的能量分布较少,因此能量熵值较小;中转速工况下,塔筒结构受其一阶自振激励的影响逐渐减弱,叶轮旋转激励增强致使塔筒结构发生强迫振动,响应信号频谱中体现出更过的倍频成分,振动能量分散,能量熵值较大;高转速工况下,叶轮旋转的倍频与塔筒结构的二阶模态频率接近或重合时导致塔筒发生共振振动,此时响应信号中的能量主要集中在二阶模态频率附近,此时的能量分布较为集中,能量熵值较小,且中间部位体现得更为明显。

根据以上分析,随着叶轮转速的变化,塔筒结构振动形式由从自振到强迫振动再到共振振动发生改变,从而致使其振动能量的强度和分布也随着发生变化。虽然机组在塔筒一阶自振频率附件设置了禁止转速区使机组能很好的实现一阶共振穿越,但在高转速区,塔筒叶轮旋转的3倍频、6倍频与塔筒结构的扭转和二阶模态频率重合从而引发机组的共振,极大地影响了机组安全运行和使用寿命,这对机组极为不利。

5 结 论

本文以某高柔塔风电机组塔筒结构现场实测的振动响应数据为基础,构建了以时域、频域以及小波包分解和能量熵计算原理相结合的信号处理分析方法,明确了塔筒结构在不同工况下的振动形式,揭示了其振动能量的分布和强度随运行因素的变化规律,主要得到以下结论:

(1)运行状态下塔筒结构的主要振动形式随环境因素和运行因素的变化而变化:低风速、低转速工况下时,塔筒结构主要受其一阶自振激励影响进行自振运动;中风速、中转速工况下时,塔筒结构主要受叶轮旋转激励影响,进行强迫振动;高风速、高转速工况下时,塔筒结构的模态频率与叶轮倍频接近或重合从而发生共振。

(2)运行状态下塔筒结构振动能量的强度及其分布与其振动形式密切相关:主要振动形式为自振时,塔筒结构能量较小,能量主要分布在一阶模态频率附近,较为集中,能量熵较小;强迫振动时,塔筒结构振动能量的强度逐渐随叶轮转速的提高而增大,能量均匀地分布在多个叶轮转频及其倍频附近,较为分散,能量熵值较大;发生共振时,振动强度明显增强且主要集中在叶轮旋转的6倍频附近,且其能量熵值小。

(3)塔筒不同高度位置处的振动强度及其能量分布不同:低风速、低转速工况下时,塔筒结构上部位置振动强度大于底部,且上部能量分布较为集中;高风速、高转速工况下时,塔筒中部位置振动能量的强度和集中度都大于上部和底部。

(4)机组的控制策略考虑了风轮转频和塔筒一阶模态频率的关系,但实际运行中,风轮的谐波激励对机组振动影响也较大,在高转速区,风轮3倍频、6倍频与塔筒的固有频率接近,容易引起机组的共振,这对机组的安全运行和使用寿命极为不利,因此在机组的塔筒设计时应考虑风轮转动倍频与其固有频率间的关系,适当加大塔筒结构固有频率与风轮3倍频和6倍频之间的安全裕量;或者通过加装阻尼器等减震降载措施来保障机组运行时的安全稳定和使用寿命。